基于高光谱指数分割的草莓硬度预测与研究

邵慧; 靳培龙; 王程; 陈冲; 胡玉霞; 刘学

doi:10.7510/jgjs.issn.1001-3806.2024.03.011

基于高光谱指数分割的草莓硬度预测与研究

邵慧^1,2, ,,
靳培龙¹,
王程^1,2,
陈冲^1,2,
胡玉霞^1,2,
刘学³

1.
安徽建筑大学电子与信息工程学院, 合肥 260601, 中国
2.
安徽建筑大学安徽省古建筑智能感知与高维建模国际联合研究中心, 合肥 230601, 中国
3.
中华通信系统有限责任公司, 北京 100000, 中国

基金项目:

安徽省高校协同创新项目 GXXT-2022-015

安徽省教育厅自然科学研究重点项目 KJ2020A0471

安徽省住房城乡建设科学技术计划资助项目 2022-YF077

安徽省住房城乡建设科学技术计划资助项目 2020-YF22

安徽省高校协同创新项目 GXXT-2021-028

光学信息与模式识别湖北省重点实验室开放课题研究基金资助项目 202204

详细信息

通讯作者:
邵慧, shaohui@ahjzu.edu.cn

中图分类号: TP391.4
计量
- 文章访问数: 9
- HTML全文浏览量: 0
- PDF下载量: 7
出版历程
- 收稿日期: 2023-04-20
- 修回日期: 2023-05-30
- 发布日期: 2024-05-24

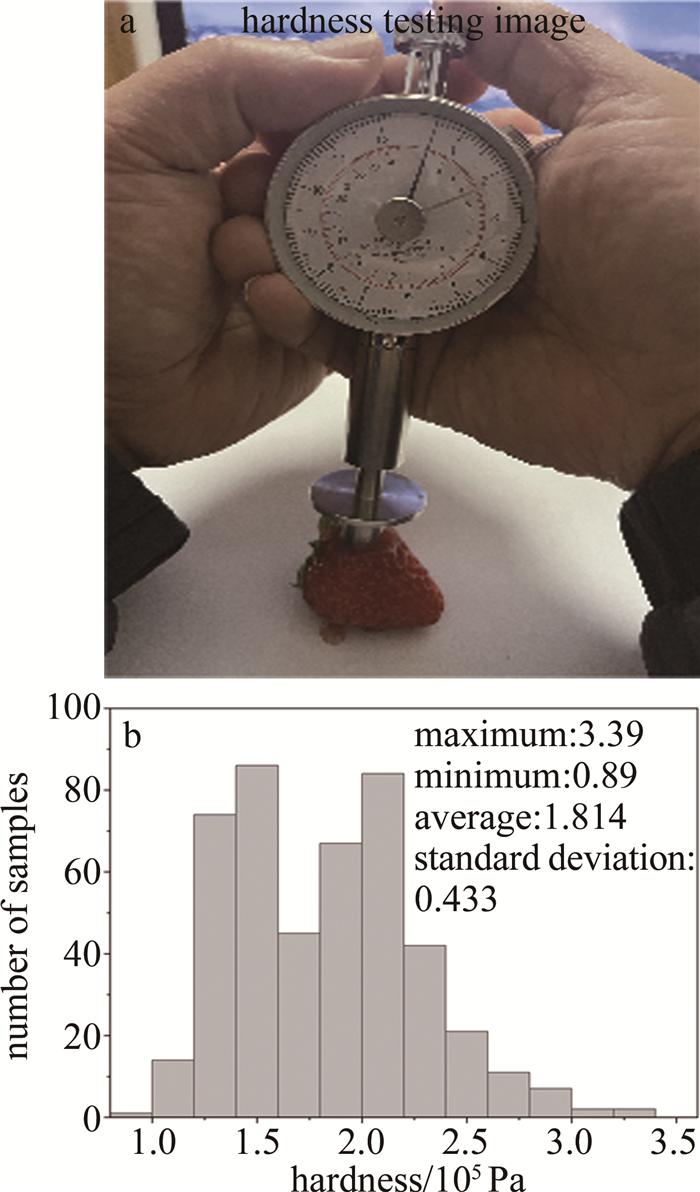
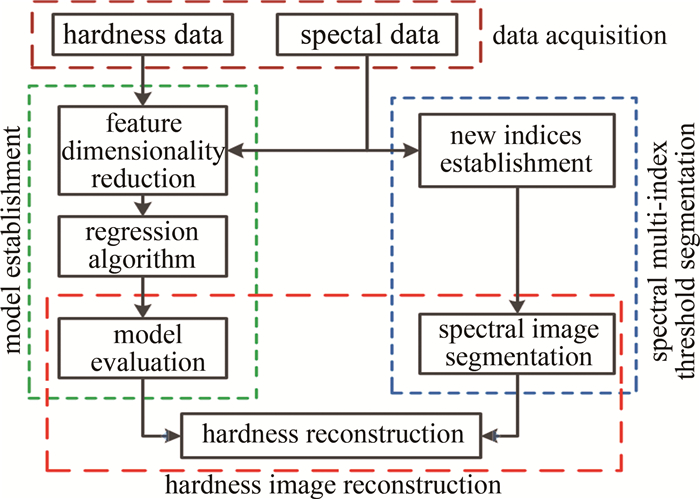
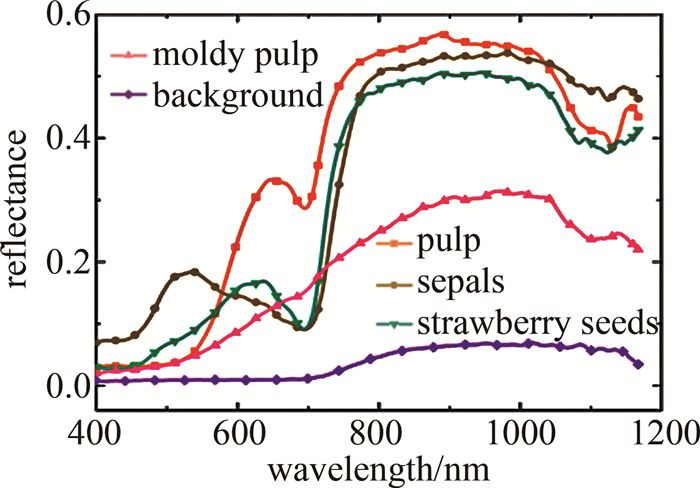
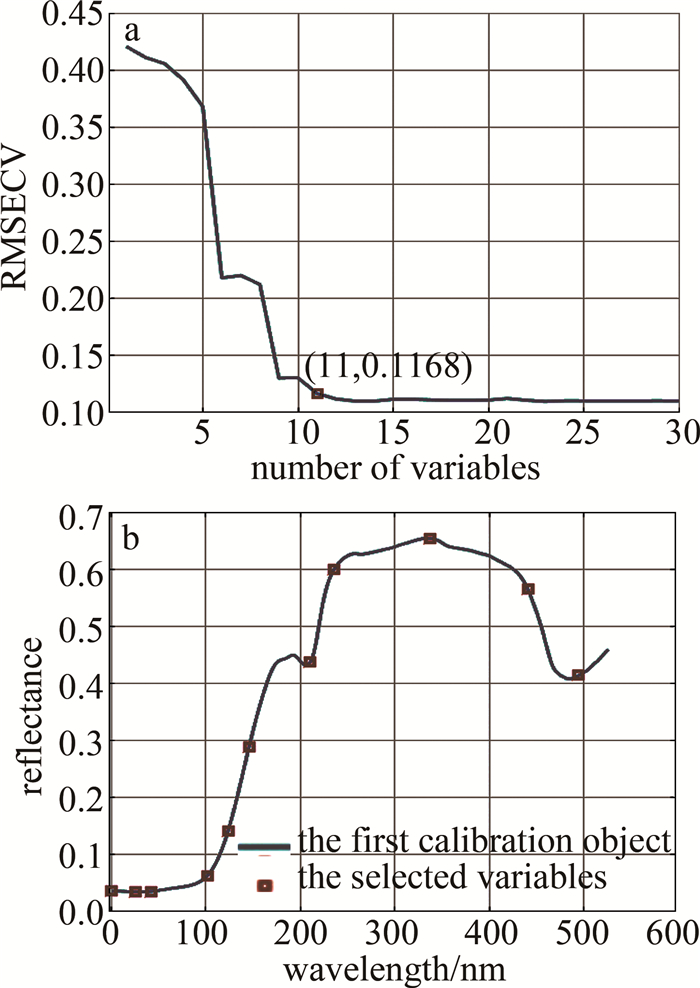
Prediction and study of strawberry hardness based on hyperspectral index segmentation

SHAO Hui^1,2, ,,
JIN Peilong¹,
WANG Cheng^1,2,
CHEN Chong^1,2,
HU Yuxia^1,2,
LIU Xue³

1.
School of Electronic and Information Engineering, Anhui Jianzhu University, Hefei 230601, China
2.
Anhui International Joint Research Center for Ancient Architecture Intellisencing and Multi-Dimensional Modeling, Anhui Jianzhu University, Hefei 230601, China
3.
China Communications System Co.Ltd., Beijing 100000, China

摘要

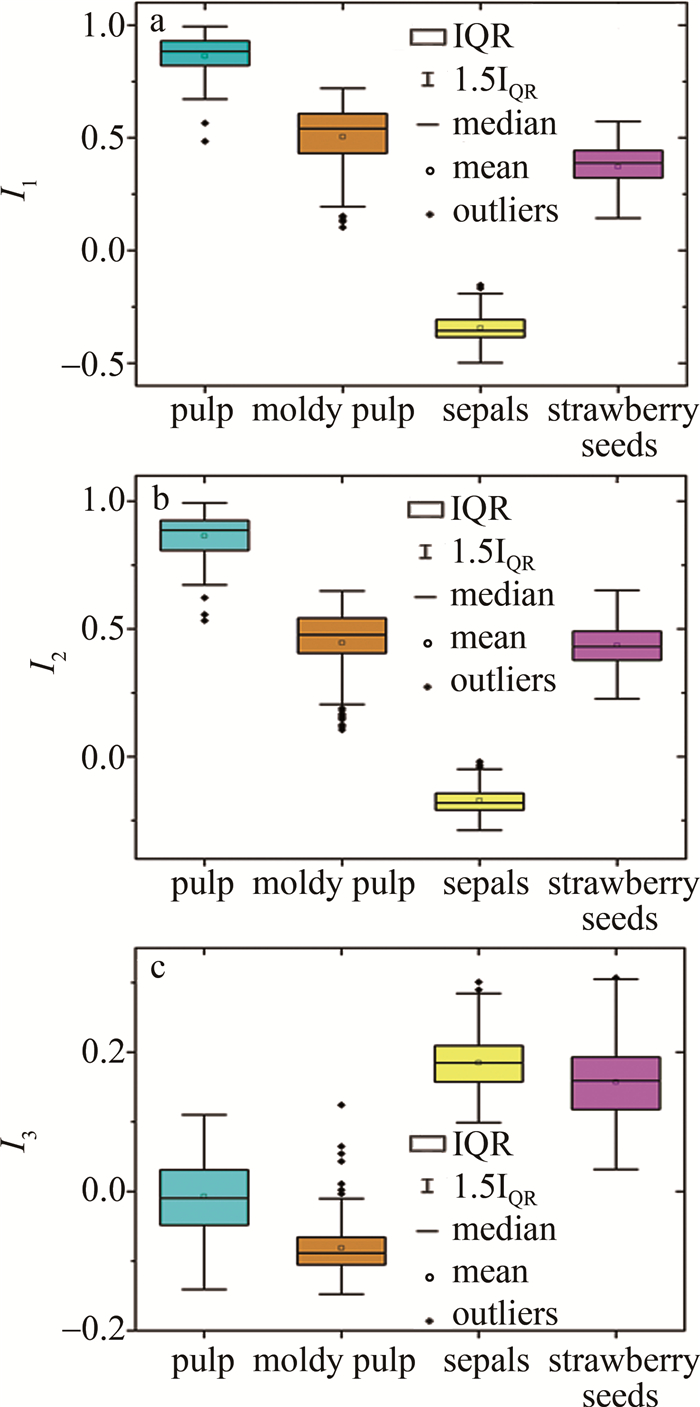
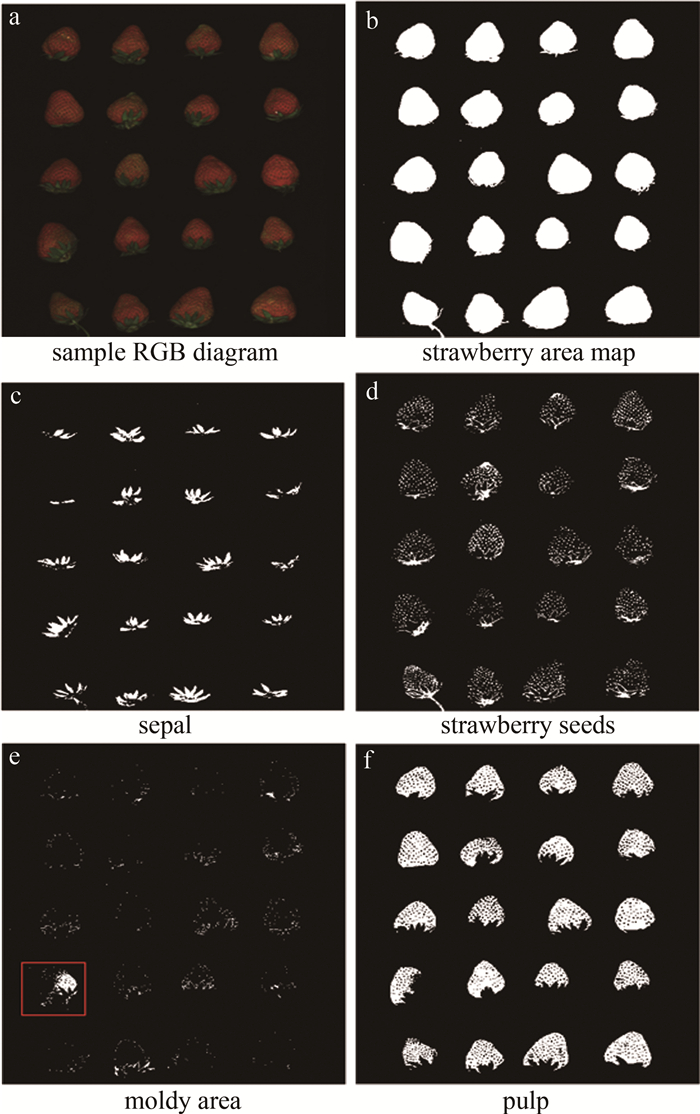
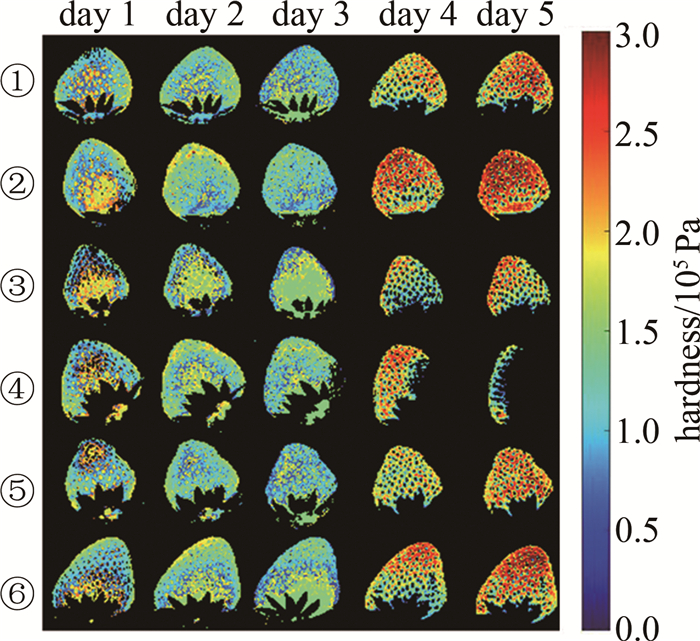
摘要: 为了快速无损检测草莓硬度, 连续5天采集了草莓高光谱数据和硬度信息, 提出一种基于高光谱多指数阈值逐层分割的硬度预测方法。首先分析各组分(果肉、霉变果肉、草莓籽和萼片)的光谱反射率差异并确定特征波段, 利用特征波段构建新的归一化特征指数, 完成分割阈值的确定, 采用逐层分割的方法以排除无关部分的干扰; 通过连续投影算法、主成分分析法及2次组合降维来降低光谱信息冗余度并提取特征, 利用随机森林与偏最小二乘法分别对原始光谱及降维后特征建立回归模型, 并确立最佳预测模型; 最后利用最佳预测模型对草莓果肉部分进行硬度拟合, 得到硬度分布图像, 实现了草莓硬度预测结果的直观显示。结果表明, 基于2次降维建立的偏最小二乘模型效果最好, 测试集和预测集的相关系数分别为0.9101和0.9099, 测试集均方根误差为0.1344。该研究为草莓硬度的无损检测和显示提供了参考。
- 光谱学 /
- 指数分割 /
- 草莓硬度 /
- 降维 /
- 硬度重建
Abstract: To achieve rapid and non-destructive detection of strawberry hardness, strawberry hyperspectral data, and hardness information were collected for five consecutive days, and a hardness prediction method based on high spectral multi-index threshold layer-by-layer segmentation was proposed. Firstly, the spectral reflectance differences of different components (pulp, moldy pulp, strawberry seeds, and sepals) were analyzed, and the characteristic bands were identified. Subsequently, new normalized feature indices were constructed based on the characteristic bands, which were selected based on spectral reflectance differences, and the segmentation thresholds were determined. The layer-by-layer segmentation method was used to eliminate the interference of irrelevant parts. Three methods(successive projections algorithm, principal component analysis, and quadratic combination dimensionality reduction) were used to reduce the spectral information redundancy and extract features. The regression models were established for the original spectral data and the reduced feature data by random forest and partial least squares regression, respectively. The best prediction model was determined to fit the hardness of the strawberry pulp. The hardness distribution image was obtained for the intuitive display of the strawberry hardness prediction result. The result shows that the partial least squares model based on quadratic dimensionality reduction yielded the best performance, with correlation coefficients of 0.9101 and 0.9099 for the test set and prediction set, respectively, and with a root-mean-square error of 0.1344 for the test set. This study provides a reference for non-destructive detection and display of strawberry hardness.
- spectroscopy /
- index segmentation /
- strawberry hardness /
- dimensionality reduction /
- hardness reconstruction

HTML全文

引言

随着低空开放，直升机的应用范围不断扩大，特别是发生重大自然灾害时执行紧急救援任务，任务地点的不确定性增强，因此保证直升机安全着陆显得尤为重要。相关领域的科研人员也开始关注直升机助降问题，直升机辅助起降技术逐渐形成一个研究的热点^[1]。无线紫外光通信作为一种新兴的无线通信方式，其在特殊场景下可实现全天候、复杂环境、高可靠性的保密通信，是直升机助降过程中辅助通信方式的最佳选择。

日盲紫外光波长为200nm~280nm，在大气信道中传输时会被气溶胶粒子散射而改变传输方向实现近直视(approximate-line-of-sight，ALOS)通信，克服了其它无线激光通信只能直视通信的不足，且有背景噪声小和抗干扰能力强等特点^[2]。尽管紫外光的大气散射特性能实现近直视通信，但散射作用会引起信号衰落加剧、增大误比特率(bit error rate, BER)，导致通信覆盖范围小、通信质量差等问题。作者^[3-4]把紫外光通信系统应用于直升机辅助起降，帮助直升机建立应急通信、备降区域锁定取和飞行引导，并提出了相应的机群间路径恢复算法。XIAO ^[5]等人针对通信系统中的各种参量提出了相应的计算方法，理论分析结果表明，在强湍流下，通信距离增加会导致闪烁衰减增大。

近几年，很多学者在研究大气湍流对无线光通信的影响，但大多数都侧重于自由空间光通信，并且都基于理论研究和仿真实验。QIANG等人^[6]根据折射率结构常数垂直分布特性，计算了湍流强度、高空位置、通信距离等因素对紫外光通信系统的影响，发现采取降低仰角可以降低闪烁指数，增加通信距离。XIAO等人^[7]进行了弱湍流对紫外光通信影响的理论研究，在开关键控(on-off keying, OOK)调制方式下分析了通信系统的误比特率性能。ZHANG等人^[8]采用gamma-gamma湍流模型仿真信道中的大气湍流，并分析了折射率结构常数对脉冲位置调制方式(pulse position modulation, PPM)的影响，结果表明，折射率结构常数越小，PPM调制的Turbo码性能越好。WANG等人^[9]验证了大气湍流对紫外光的衰减作用，中等强度湍流(C_n²=10^-14m^-2/3)下比无湍流时信噪比(signal-to-noise ratio, SNR)降低20dB，并通过增大接收孔径的方法降低了湍流对通信系统的衰减。WANG^[10]根据紫外光通信的特点建立紫外光通信弱湍流下的分集接收模型，并在实验室环境下进行了仿真分析和实验验证，结果表明, 分集接收能提升通信系统误比特率性能。由此可以看出，国内紫外光通信系统相关研究大多为理论分析阶段，且处于实验室环境下，在特殊应用场景下的研究就更鲜有人涉及。

虽然相关学者对紫外光通信进行了很多实验室环境下的探究，在直升机助降应用中，中强湍流对紫外光通信的影响很少有人进行分析研究，且尚未找到一种合适的方法来进行抑制。本文中首先通过紫外光近直视通信系统修正模型分析了强湍流对紫外光通信的影响，然后采用分集接收技术来抑制大气湍流效应，降低了通信系统误比特率，并对比3种合并方式的性能差异，为推动紫外光通信的实际应用提供理论支持。

1. 助降场景下紫外光通信模型

1.1 直升机助降引导模型

直升机助降模型如图 1所示。直升机备降区域有A, B, C, D 4个定位点，分别放置4个不同波段的紫外发光二极管(light emitting diode, LED)作为发射装置，E为直升机位置。在直升机降落时，日盲紫外光不仅会受到大气的吸收和散射作用，直升机尾翼气流引起的湍流效应也使得接收到的紫外光信号闪烁指数变大，通信系统误比特率增大^[11]。在紫外光引导直升机助降过程中，直升机先到达备降区域，接收装置悬挂在直升机底部，接收地面4个定位点发来的位置信息。飞行员根据得到的地面信息，调整机身的降落姿态到达最佳着陆点，实现安全快速降落目的。

Figure 1. Model of helicopter assisted landing

下载: 全尺寸图片幻灯片

1.2 紫外光近直视通信模型

直升机降落过程通信系统收发端相对位置是动态变化的，并且水平距离和高度差会一直存在，直至安全降落。因其收发端的相对位置是时变的，紫外光直视和非直视通信传统模型无法很好地拟合该应用场景，故定义添加了水平距离和垂直高度变量后的修正模型为紫外光近直视通信模型。紫外光通信应用在直升机助降过程中，根据相对位置的不同可分为3种：水平通信方式、垂直通信方式和斜程通信方式。其中水平通信和垂直通信可分别看作是斜程通信垂直高度为0和水平距离为0时的特殊形式，在此只选取斜程通信进行研究, 该通信方式如图 2所示。当以T作为发送端、R为接收端时，从图 2中能看出, 收发端之间高度差为h，相对水平距离为r，此时为斜程通信。若以地平面作为参考面，定义发散角为φ₁，接收视场角为φ₂，发送仰角为θ₁，接收仰角为θ₂，θ₁′为斜程通信方式中的发送仰角，θ₂′为斜程通信方式中接收仰角，有效散射体为V，发送端到接收端的直线距离表示为r₀，则发送端到有效散射体的距离为r₁，有效散射体到接收端的距离为r₂。设接收端R与发送端T相对水平线和相对垂直高度线构成直角三角形^[12]，两直角边分别为r和h，根据勾股定理可得收发端的直线距离r₀，即 ${r_0} = \sqrt {{r^2} + {h^2}}$ 。

Figure 2. Model of UV slope communication

下载: 全尺寸图片幻灯片

1.3 大气折射率结构常数

对于局部均匀的大气湍流，其强弱通常用结构常数C_n²来表示。一般水平路径上，高度和风速基本是已知的，所以C_n²为常数；直升机助降的斜程通信系统中，高度和风速都是不均匀的，所以C_n²也不是恒定值，其变化受海拔、气温、风速、气压等有关。常用的C_n²模型有很多，国际电联给出一种新的垂直分布模型^[13]：

$\begin{array}{*{20}{c}} {C_n^2\left( h \right) = 8.148 \times {{10}^{ - 56}}{v_{{\rm{RMS}}}}^2{h^2}\exp \left( { - \frac{h}{{100}}} \right) + }\\ {2.7 \times {{10}^{ - 16}}\exp \left( { - \frac{h}{{1500}}} \right) + C_0^2\exp \left( { - \frac{h}{{100}}} \right)} \end{array}$

(1)

式中，C₀²是近地面的大气结构常数，v_RMS是垂直路径上的均方根风速，且 ${v_{{\rm{RMS}}}} = \sqrt {{v_g}^2 + 30.69{v_g} + 348.91}$ 。 ${v_{\rm{g}}} = 3 + 17{\rm{exp}}\left[{- {{\left( {\frac{h}{{1000}} - 12.5} \right)}^2}/16} \right]$ , h表示海拔高度(m)。近地面处C_n²的标准范围为10^-12m^－2/3(强湍流)~10^－18m^－2/3(弱湍流)。大气对流强度是影响大气湍流强度的主要因素，海拔高度h不断变大，C_n²随之减小。此外，在直升机降落过程中，紫外光近直视通信信道中的C_n²是随着海拔高度、温度和风速等因素不断变化的，直升机尾流风速也能使C_n²变大，强湍流导致光信号的闪烁指数变大，误比特率上升，降低通信系统稳定性，严重时可能会使通信中断。

1.4 近直视通信链路强湍流信道模型

大气湍流的相关论述中多是点对点的直视通信，其信号强度分布模型也是在直视通信链路场景下进行探究，针对自由空间光直视通信的系统模型，因其信号强度分布模型不同，在近直视通信系统中无法直接使用。本文中将紫外光近直视通信模型当作是两段或多段点对点直视通信的组合模型，通过建立一个联合概率分布函数来计算接收端的信号强度分布^[14]。一般认为，C_n²=10^－18m^－2/3时为弱湍流，服从对数正态分布；在中强湍流下，更多采用gamma-gamma模型，从弱湍流到强湍流都能很好地拟合接收光强的分布特性，其概率密度函数可表示为^[15]：

$f{\left( I \right)_{{\rm{GG}}}} = \frac{{2{{\left( {\alpha \beta } \right)}^{\frac{{\alpha + \beta }}{2}}}}}{{{\rm{\Gamma }}\left( \alpha \right){\rm{\Gamma }}\left( \beta \right)}}{I^{\frac{{\alpha + \beta }}{2} - 1}}{{\rm{K}}_{\alpha ,\beta }}\left( {2\sqrt {\alpha \beta I} } \right)$

(2)

式中，Γ()为gamma函数，K()为修正的贝塞尔函数，α表示光强闪烁指数强度大小的外尺度，β表示光强闪烁指数强度大小的内尺度，I为接收端接收到的信号强度。当β=1时，双gamma分布模型转化为K分布模型，其概率密度函数可表示为：

$f{\left( I \right)_{\rm{K}}} = \frac{{2{\alpha ^{\frac{{\alpha + 1}}{2}}}}}{{{\rm{\Gamma }}\left( \alpha \right)}}{I^{\frac{{\alpha - 1}}{2}}}{{\rm{K}}_{\alpha ,1}}\left( {2\sqrt {\alpha I} } \right)$

(3)

式中，α是信道参量，其与离散散射体的有效数目相关，α随湍流强度变化而变化，湍流强度越强其值越小。则K分布下的光强闪烁指数为：

$\sigma _I^2 = \frac{{E\left( {{I^2}} \right) - {E^2}\left( I \right)}}{{{E^2}\left( I \right)}} = \frac{{\alpha + 2}}{\alpha }$

(4)

式中，E为接收信号强度。由(4)式可以看出，σ_I²随信道参量α的变化而变化，湍流强度越大闪烁指数σ_I²越大。

紫外光近直视通信链路模型如图 2所示。在近直视通信链路模型中，设I_r₁是从发射端到达散射体的平均信号强度，I_r₂是接收端的平均信号强度。从发射端到达有效散射体的信号强度概率密度函数为：

$f{\left( {{I_{{r_1}}}} \right)_{\rm{K}}} = \frac{{2{\alpha _{{r_1}}}^{\frac{{\left( {{a_{{r_1}}} - 1} \right)}}{2}}}}{{{\rm{\Gamma }}\left( {{\alpha _{{r_1}}}} \right)}}{I_{{r_1}}}^{\frac{{\left( {{a_{{r_1}}} - 1} \right)}}{2}}{{\rm{K}}_{{\alpha _{{r_1}}},1}}\left( {2\sqrt {{\alpha _{{r_1}}}{I_{{r_1}}}} } \right)$

(5)

式中，α_r₁为r₁路径的光强闪烁。从有效散射体到接收端的信号强度的条件概率密度函数为：

$f{\left( {{I_{{r_2}}}\left| {{I_{{r_1}}}} \right.} \right)_{\rm{K}}} = \frac{{2{\alpha _{{r_2}}}^{\frac{{{a_{{r_2}}} + 1}}{2}}}}{{{\rm{\Gamma }}\left( {{\alpha _{{r_2}}}} \right)}}{I_{{r_2}}}^{\frac{{{a_{{r_2}}} - 1}}{2}}{{\rm{K}}_{{\alpha _{{r_2}}},1}}\left( {2\sqrt {{\alpha _{{r_2}}}{I_{{r_2}}}} } \right)$

(6)

式中，α_r₂为r₂路径的光强闪烁。综合(5)式和(6)式，得到紫外光近直视通信系统中接收端信号强度的边缘分布概率密度函数为^[16]：

$f\left( {{I_{{r_2}}}} \right) = \int {f\left( {{I_{{r_2}}}\left| {{I_{{r_1}}}} \right.} \right)f\left( {{I_{{r_1}}}} \right){\rm{d}}\left( {{I_{{r_1}}}} \right)}$

(7)

2. 系统误比特率性能分析

根据TAYLOR的冻结假设，与光传播的速度相比，大气湍流的运动是极其缓慢的，因此湍流信道是一种准静态的大气信道^[17]。假设信道只存在高斯噪声，则采用OOK调制时的通信系统模型可表示为^[15]:

$y = x\eta I + v\left( I \right)$

(8)

式中，y为接收端得到的信号强度；x表示开关键控调制信号(0, 1)，η为光电转换效率；Ι为接收器接收到的光强；v(I)为加性高斯白噪声。定义系统信噪比γ为：

$\gamma = \frac{{{{\left( {\eta I} \right)}^2}}}{{2\sigma _v^2}}$

(9)

式中，σ_v²为零均值加性高斯白噪声v(I)的方差，且 $\sigma _v^2 = \frac{{{N_0}}}{2}$ ，N₀是均值为零的噪声功率。

无线紫外光通信系统调制方式采用OOK，其误比特率P_e表示为^[18]：

${P_{\rm{e}}} = p\left( 0 \right)p\left( {e\left| 0 \right.} \right) + p\left( 1 \right)p\left( {e\left| 1 \right.} \right)$

(10)

式中，p(0)是系统发送0的概率，p(1)是系统发送1的概率；p(e|0)为发送0时接收端接收到信号的条件概率，p(e|1)为发送1时接收端收到信号的条件概率。系统发送1和0的概率是相同的，即p(0)=p(1)= $\frac{1}{2}$ ，且 $p\left( {e\left| 0 \right.} \right){\rm{ = }}p\left( {e\left| 1 \right.} \right) = Q\left( {\frac{{\eta \mathit{ I}}}{{\sqrt {2{N_0}} }}} \right)$ 。则OOK调制方式下的系统平均误比特率为：

${P_{\rm{e}}} = \int_0^\infty {f\left( I \right)Q\left( {\frac{{\eta I}}{{\sqrt {2{N_0}} }}} \right){\rm{d}}I}$

(11)

已知关系式erfc(x)=2Q( $\sqrt {2x}$ )，erfc()为误差函数。将概率密度函数f(I_r₂)和Q函数都带入(11)式, 可得K分布信道模型中的平均误比特率，公式为：

${P_{{\rm{e,K}}}} = \frac{1}{2}\int_0^\infty {f\left( {{I_{{r_2}}}} \right){\rm{erfc}}\left( {\frac{{\eta {I_{{r_2}}}}}{{\sqrt {2{N_0}} }}} \right){\rm{d}}{I_{{r_2}}}}$

(12)

3. 3种分集合并方法误比特率性能分析

假设输入支路有N条，令第i条支路接收信号为x_i(t)(i=1, 2, …, N)，第i条接收支路的加权系数为ω_i。则分集合并后的输出为：

$\begin{array}{*{20}{c}} {y\left( t \right) = {\omega _1}{x_1}\left( t \right) + {\omega _2}{x_2}\left( t \right) + \cdots + }\\ {{\omega _N}{x_N}\left( t \right) = \sum\limits_{i = 1}^N {{\omega _i}{x_i}\left( t \right)} } \end{array}$

(13)

式中，t为时间。接收端通过某种加权方式将携带相同信息的多路相互独立的信号进行合并，达到提高通信系统信号信噪比的目的，这就是合并技术，合并方式的分类是由加权系数ω_i所决定的。常用的合并方式有：最大比合并(maximum ratio combination, MRC)、等增益合并(equal gain merging, EGC)和选择性合并(selective merging, SC)。

3.1 最大比合并方式

最大比合并的原理是3种合并方式中最复杂的，根据各支路的加权系数与该支路的信噪比成正比的特点，每条支路的信号都与该支路的加权系数相乘，然后各路相加，信噪比大的支路信号占据合并输出信号的比例大，对系统信噪比性能的提升明显。合并输出的信噪比为^[15]：

${\gamma _{{\rm{MRC}}}} = {\left( {\frac{\eta }{{\sqrt {2N} }}} \right)^2}\sum\limits_{i = 1}^N {\frac{{I_i^2}}{{\sigma _v^2}}} = \sum\limits_{i = 1}^N {{\gamma _i}}$

(14)

式中, 某一条信噪比可表示为 ${\gamma _i} = {(\eta {\mathit{I}_i}\sqrt {2N{\sigma _v}^2} )^2}$ ，MRC合并的误比特率公式为：

${P_{{\rm{e,MRC}}}} = \int_0^\infty {f\left( {{I_{{r_2}}}} \right)Q\left( {\frac{\eta }{{\sqrt {2N{N_0}} }}\sqrt {\sum\limits_{i = 1}^N {{I_{{r_2},i}}^2} } } \right){\rm{d}}{I_{{r_2}}}}$

(15)

式中，I_{r₂, i}为第i路近直视链路的接收信号强度。利用 $Q\left( x \right) \approx \frac{1}{{12}}{\rm{exp}}\left( { - \frac{{{x^2}}}{2}} \right) + \frac{1}{4}{\rm{exp}}\left( { - \frac{{2{x^2}}}{3}} \right)$ 对上式积分进行化简可得：

$\begin{array}{*{20}{c}} {{P_{\rm{e}}} \approx \frac{1}{{12}}\prod\limits_{i = 1}^N {\int_0^\infty {f\left( {{I_{{r_2},i}}} \right)\exp \left( { - \frac{{{\eta ^2}}}{{4N{N_0}}}{I_{{r_2},i}}^2} \right){\rm{d}}{I_{{r_2},i}}} } + }\\ {\frac{1}{4}\prod\limits_{i = 1}^N {\int_0^\infty {f\left( {{I_{{r_2},i}}} \right)\exp \left( { - \frac{{{\eta ^2}}}{{3N{N_0}}}{I_{{r_2},i}}^2} \right){\rm{d}}{I_{{r_2},i}}} } } \end{array}$

(16)

3.2 等增益合并方式

等增益合并可以看作是最大比合并的一种特殊情况，它的各支路信号的加权系数都相等，且都为定值，类比最大比合并输出信噪比公式，则EGC合并输出的信噪比可表示为：

${\gamma _{{\rm{EGC}}}} = {\left( {\frac{\eta }{{\sqrt {2N\sigma _v^2} }}} \right)^2}\sum\limits_{i = 1}^N {{I_i}^2}$

(17)

把信噪比(17)式带入误比特率(12)式，并进行化简，可以得出等增益合并方式的误比特率公式为：

${P_{{\rm{e,EGC}}}} = \int_0^\infty {f\left( {{I_{{r_2}}}} \right)Q\left( {\frac{\eta }{{N\sqrt {2{N_0}} }}\sum\limits_{i = 1}^N {{I_{{r_2},i}}} } \right){\rm{d}}{I_{{r_2}}}}$

(18)

利用 $Q\left( x \right) \approx \frac{1}{{12}}{\rm{exp}}\left( { - \frac{{{x^2}}}{2}} \right) + \frac{1}{4}{\rm{exp}}\left( { - \frac{{2{x^2}}}{3}} \right)$ 对上式积分进行化简可得：

$\begin{array}{*{20}{c}} {{P_{{\rm{e,EGC}}}} \approx \frac{1}{{12}}{{\left[ {\int_0^\infty {f\left( {{I_{{r_2}}}} \right)\exp \left( { - \frac{{{\eta ^2}{I_{{r_2}}}^2}}{{4N{N_0}}}} \right){\rm{d}}{I_{{r_2}}}} } \right]}^N} + }\\ {\frac{1}{4}{{\left[ {\int_0^\infty {f\left( {{I_{{r_2}}}} \right)\exp \left( { - \frac{{{\eta ^2}{I_{{r_2}}}^2}}{{3N{N_0}}}} \right){\rm{d}}{I_{{r_2}}}} } \right]}^N}} \end{array}$

(19)

3.3 选择合并方式

选择合并是上述3种合并技术中最简单的1种，它的原理是监测所有支路信号的信噪比，只需要从N条支路中选取1条支路作为输出，与MRC和EGC相比合并算法复杂度降低。但是该合并方式牺牲了合并所带来的增益，并且需要实时监测各支路，选出信噪比最大的支路作为输出。其输出信号为：

${I_{{\rm{SC}}}} = \max \left\{ {{I_1},{I_2},{I_3}, \cdots ,{I_N}} \right\}$

(20)

在所有加权系数中，只有信噪比最大的一路为1，其余的都为0，即:

${\omega _i} = \left\{ \begin{array}{l} 1,\left( {{\gamma _{{\rm{SC}}}} = \max \left\{ {{I_1},{I_2},{I_3}, \cdots ,{I_N}} \right\}} \right)\\ 0,\left( {{\rm{else}}} \right) \end{array} \right.$

(21)

式中，γ_SC为选择合并的信噪比。gamma-gamma湍流模型下其概率密度函数为：

${f_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right) = \frac{{{\rm{d}}{F_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right)}}{{{\rm{d}}{I_{{r_2}}}}} = N{F_{{\rm{SC}}}}{\left( {{I_{{r_2}}}} \right)^{N - 1}}f\left( {{I_{{r_2}}}} \right)$

(22)

式中，F_SC(I_r₂)为选择合并的N条支路输出的分布函数，选择合并的平均误比特率公式可以表示为：

${P_{{\rm{e,SC}}}} = \int_0^\infty {{f_{{\rm{SC}}}}\left( {{I_{{r_2}}}} \right)Q\left( {\frac{{\eta {I_{{r_2},{\rm{SC}}}}}}{{2\sqrt {N{N_0}} }}} \right){\rm{d}}{I_{{r_2},{\rm{SC}}}}}$

(23)

式中，I_{r₂, SC}为近直视通信选择合并时的接收信号强度。把概率密度函数f(I_r₂)带入(23)式可得：

$\begin{array}{*{20}{c}} {{P_{{\rm{e,SC}}}} = \int_0^\infty {N{F_{{\rm{SC}}}}{{\left( {{I_{{r_2}}}} \right)}^{N - 1}}f\left( {{I_{{r_2}}}} \right)} \times }\\ {Q\left( {\frac{{\eta {I_{{r_2},{\rm{SC}}}}}}{{2\sqrt {N{N_0}} }}} \right){\rm{d}}{I_{{r_2},{\rm{SC}}}}} \end{array}$

(24)

4. 仿真分析和实验验证

首先仿真分析风速和距离对湍流强度的影响。根据第3节中推导出的MRC, EGC和SC 3种分集合并方法的误比特率公式，仿真分析湍流效应对通信系统误比特率性能的影响，以及这3种合并方法在直升机助降紫外光近直视通信系统中对强湍流效应的抑制作用，并对比了3种不同合并方式之间的性能差异。部分仿真参量的选取如表 1所示。通信速率设定为100kbit/s。

Table 1. Parameters of the system simulation

parameter	value
receiving aperture area A_r	1.77cm²
attenuation coefficient K_e	1.961×10^-3
scattering coefficient K_s	0.759×10^-3
photoelectric response P_r	48mA/W

下载: 导出CSV

| 显示表格

根据(1)式可知，大气折射率结构常数C_n²增大，对应的湍流强度也会增强。图 3为大气折射率结构常数垂直分布仿真。从图中可以看出，距离地面越近，大气湍流越强，仿真结果与公式分析基本相符。因此在直升机降落过程中，湍流效应对通信系统的影响是不可忽略的，通过抑制湍流效应能有效改善通信系统的性能。

$Figure 3. Distribution diagram of atmospheric refractive index structure constant$

Figure 3. Distribution diagram of atmospheric refractive index structure constant

下载: 全尺寸图片幻灯片

当水平ALOS通信时，以C_n²表征湍流特性，而在垂直ALOS通信时，由于C_n²是随高度变化的，因此采用C₀²表征湍流特性。图 4a为不同湍流强度下水平近直视通信的接收端信号强度概率密度函数分布(归一化信号强度)。收发仰角均为60°，水平距离r=100m，湍流强度从10^-16m^-2/3~10^-13m^-2/3, 信号强度发散，并剧烈衰减，当湍流强度增强到10^-13m^-2/3时，信号能量衰减到几乎无法实现通信的程度。由此可以看出, 湍流效应对无线紫外光水平ALOS通信接收光强的概率密度分布影响较大。

Figure 4. Effect of horizontal distance and vertical height on UV communication

a—horizontal ALOS communication b—vertical ALOS communication

下载: 全尺寸图片幻灯片

图 4b为不同湍流强度下垂直近直视通信的信号强度概率密度函数分布(归一化信号强度)。在垂直ALOS通信时，C_n²是不定的，所以选取地面大气折射率结构常数表征湍流强度，收发仰角均为60°，水平距离h=100m，湍流强度从10^-16m^-2/3~10^-13m^-2/3，信号强度发散，在强湍流为10^-15m^-2/3和10^-14m^-2/3时，垂直通信和水平通信的概率密度相近，信号强度衰减也很剧烈，当湍流强度增强到10^-13m^-2/3时，信号能量发散严重。由此可以看出，湍流效应对无线紫外光垂直ALOS通信接收光强的概率密度分布影响较大。

图 5仿真了紫外光近直视通信系统闪烁指数σ_I²对误比特率的影响。由第1.4节中可知, 湍流强度与闪烁指数σ_I²的关系，定义湍流强度越强，闪烁指数σ_I²越大；一般认为在无线光通信中当闪烁指数σ_I²>1时大气湍流为强湍流，所以分别选取了σ_I²为1.02，2，4，6，8这5种闪烁指数所对应的湍流强度进行分析。随着闪烁指数σ_I²增强，通信系统误比特率逐渐增大，说明湍流强度越大，通信系统的误比特率性能越差。从图中还可以看出, 湍流影响下的信噪比在60dB时, 误比特率才达到通信系统的最低要求10^-3，由此可见，在直升机助降紫外光近直视通信系统中，有效抑制大气湍流效应带来的影响很有必要。

Figure 5. Influence of scintillation index on BER

下载: 全尺寸图片幻灯片

图 6a是对MRC合并方式在不同接收天线和信道参量下系统误比特率性能仿真图。由图可知，当N=1时, 即为未分集接收，湍流效应越强，系统性能越差，未采用分集接收时误比特率要达到10^-3，信噪比需要58dB，而N为2和3时, 分别只需要36dB，25dB，这说明MRC合并方式能明显提升系统性能。当N为1~3时，MRC合并在两种湍流强度下系统性能的差距也逐渐变大，说明MRC合并技术可以有效抑制湍流效应带来的影响，接收天线越多对湍流的抑制作用就越明显。

Figure 6. Performance simulation of three kinds of combining methods

a—MRC b—EGC c—SC

下载: 全尺寸图片幻灯片

图 6b是EGC合并方式下接收天线和信道参量系统误比特率性能仿真图。在信道参量相同情况下, 未采用分集接收时误比特率要达到10^-3，信噪比需要58dB，而N为2和3时, 分别只需要40dB，27dB，说明EGC合并方式能明显提升系统性能。当N为1~3时，两种湍流强度下EGC合并方式对性能的提升效果也不同，接收天线越多对湍流的抑制作用就越明显。

图 6c是对SC合并方式在不同接收天线和信道参量下系统误比特率性能仿真图。由图可知，湍流强度变大时，系统性能变差，未采用分集接收时误比特率要达到10^-3，信噪比需要58dB，而N为2和3时, 分别只需要42dB，29dB，说明SC合并方式能明显提升系统性能。不同湍流强度下，SC合并对系统性能的提升程度不同，说明SC合并技术能有效抑制湍流效应带来的影响，接收天线越多, 对湍流的抑制作用就越明显。

图 7a为MRC合并方式和EGC合并方式的误比特率性能对比仿真图。从图中可以看出, 虽然MRC合并方式和EGC合并方式都能提升系统误比特率性能，但MRC合并方式的效果要比EGC合并方式略好一点，性能差距约为4dB，不过随着接收天线数的增加, 这种差距会扩大。同样的接收天线数时，MRC合并方式也比EGC合并方式对湍流的抑制作用稍强，不过两者对系统的误比特率性能提升差距很小。

Figure 7. Performance comparison of three kinds of combining methods

a—comparison of MRC merge and EGC merge performance b—comparison of EGC merge and SC merge performance

下载: 全尺寸图片幻灯片

图 7b为EGC合并方式和SC合并方式的误比特率性能对比仿真图。可以看出, SC合并方式和EGC合并方式都能在一定程度上提升系统性能，抑制湍流效应。在相同接收天线和信达参量时，EGC合并方式比SC合并方式都对系统性能的提升大2dB左右，并且随着接收天线数的增加，EGC合并方式和SC合并方式对系统性能的提升差距逐渐变大。

5. 结论

直升机助降场景中紫外光近直视通信系统性能会受到大气湍流的影响，推导出接收光强概率密度函数公式，建立强湍流信道下紫外光近直视通信修正模型。随着斜程通信相对位置增大，通信系统的信号强度概率密度函数分布分散，能量衰减严重，大气湍流效应严重影响该通信方式下的系统误比特率性能。通过给出的近直视通信系统在3种分集合并方式的误比特率公式得出：MRC, EGC, SC这3种合并方式都能对大气湍流效应有一定的抑制作用，随着分集天线的增加3种合并方式的对系统性能的提升也越来越大。说明分集接收技术能有效抑制强湍流效应，提升通信系统的稳定性和抗衰落性能，成为无线紫外光通信应用于直升机助降的有力保障。考虑到MRC合并方式需要计算接收信号的信噪比，计算复杂度较高，EGC和SC相对较为简单，但EGC性能相对于SC要高2dB左右，因此, 在实际应用中要根据具体需求做出合理选择。

图 1 草莓样本及不同组成示意图

Figure 1. Schematic diagram of strawberry samples and different compositions

下载: 全尺寸图片幻灯片

图 2 样本硬度测量

Figure 2. Sample hardness measurement

下载: 全尺寸图片幻灯片

图 3 本文中方法框图

Figure 3. Block diagram of the methodology for this article

下载: 全尺寸图片幻灯片

图 4 不同组分光谱特征波长曲线

Figure 4. Spectral feature curves of different components

下载: 全尺寸图片幻灯片

图 5 SPA选择特征波长

Figure 5. Feature wavelength selection based on SPA

下载: 全尺寸图片幻灯片

图 6 基于最优PLS与RF建立的硬度模型

Figure 6. Hardness model based on optimal PLS and RF

下载: 全尺寸图片幻灯片

图 7 样本各指数分布情况

Figure 7. Distribution of the sample by index

下载: 全尺寸图片幻灯片

图 8 各组分-背景二值化结果

Figure 8. Component-background binarization results

下载: 全尺寸图片幻灯片

图 9 草莓硬度重建图像

Figure 9. Strawberry hardness reconstruction image

下载: 全尺寸图片幻灯片

表 1 PCA降维特征贡献度

Table 1 Feature contribution in PCA

number of features	cumulative contribution rate
1	0.8669
2	0.9473
3	0.9801
4	0.9920
5	0.9970
6	0.9983
7	0.9991
8	0.9996
9	0.9997
10	0.9997

下载: 导出CSV

表 2 SPA-PCA降维特征贡献度

Table 2 Feature contribution in SPA-PCA

number of features	cumulative contribution rate
1	0.7377
2	0.9300
3	0.9745
4	0.9902
5	0.9972
6	0.9991
7	0.9997
8	0.9997

下载: 导出CSV

表 3 基于PLS的模型建模结果

Table 3 PLS-based model modeling results

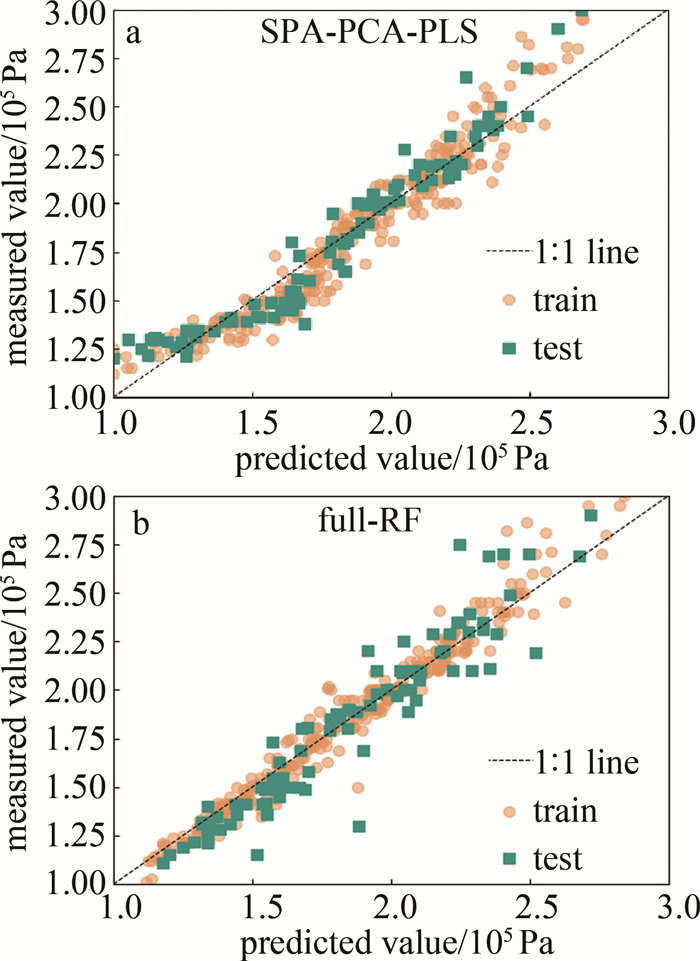
modeling methods	CCC	CCP	RMSEC	RMSEP	RPD
full-PLS	0.9084	0.8636	0.1307	0.1592	2.4973
PCA-PLS	0.9111	0.9047	0.1283	0.1352	3.1019
SPA-PLS	0.9069	0.8700	0.1323	0.1529	2.6451
SPA-PCA-PLS	0.9101	0.9099	0.1290	0.1344	3.2623

下载: 导出CSV

表 4 基于RF的模型建模结果

Table 4 RF-based model modeling results

modeling methods	CCC	CCP	RMSEC	RMSEP	RPD
full-RF	0.9611	0.8889	0.0845	0.1491	2.5344
SPA-RF	0.9321	0.8667	0.1143	0.1473	2.1535
PCA-RF	0.9522	0.8735	0.0926	0.1644	2.0531
SPA-PCA-RF	0.9620	0.8158	0.0837	0.1891	1.7907

下载: 导出CSV

参考文献(27)

[1]	白胜, 朱润华, 阳圣莹, 等. 不同草莓品种营养成分比较与品种筛选[J]. 山西农业科学, 2020, 48(1): 64-67. https://www.cnki.com.cn/Article/CJFDTOTAL-SXLX202001018.htm BAI Sh, ZHU R H, YANG Sh Y, et al. Nutrients comparison and screening of different strawberry varieties[J]. Journal of Shanxi Agricultural Sciences, 2020, 48(1): 64-67(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SXLX202001018.htm
[2]	AFRIN S, GASPARRINI M, FORBES-HERNANDEZ T Y, et al. Promising health benefits of the strawberry: A focus on clinical studies[J]. Journal of Agricultural and Food Chemistry, 2016, 64(22): 4435-4449. DOI: 10.1021/acs.jafc.6b00857
[3]	刘凯丽, 郑洪健, 黄敏, 等. 云南香格里拉3个草莓品种的感官品质及耐储藏性对比分析[J]. 昆明学院学报, 2022, 44(3): 87-92. https://www.cnki.com.cn/Article/CJFDTOTAL-KMSG202203017.htm LIU K L, ZHENG H J, HUANG M, et al. Comparative analysis of sensory quality and storage tolerance of three strawberry varieties in Yunnan Shangri-La[J]. Journal of Kunming University, 2022, 44(3): 87-92(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KMSG202203017.htm
[4]	郝乾坤, 王智民, 童开林. 外源海藻糖对草莓保鲜效果的影响[J]. 陕西农业科学, 2022, 68(8): 84-87. https://www.cnki.com.cn/Article/CJFDTOTAL-SNKX202208017.htm HAO Q K, WANG Zh M, TONG K L. Effect of exogenous trehalose on preservation of strawberry[J]. Shaanxi Journal of Agricultural Sciences, 2022, 68(8): 84-87(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SNKX202208017.htm
[5]	陈卓, 宋俏微, 张水洞, 等. 氧化淀粉的抑菌效果及草莓涂膜保鲜应用[J]. 食品科学, 2022, 43(21): 324-331. https://www.cnki.com.cn/Article/CJFDTOTAL-SPKX202221039.htm CHEN Zh, SONG Q W, ZHANG Sh D, et al. Antimicrobial effect of oxidized starch and its application as a coating for strawberry preservation[J]. Food Science, 2022, 43(21): 324-331(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SPKX202221039.htm
[6]	LIU Y, WU Q W, HUANG J L, et al. Comparison of apple firmness prediction models based on non-destructive acoustic signal[J]. International Journal of Food Science & Technology, 2021, 56(12): 6443-6450.
[7]	陈广大, 刘德君, 李天旭, 等. 便携式水果硬度测量仪的设计[J]. 中国农机化学报, 2016, 37(7): 85-88. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJH201607019.htm CHEN G D, LIU D J, LI T X, et al. Design of the portable fruit hardness measuring instrument[J]. Journal of Chinese Agricultural Mechanization, 2016, 37(7): 85-88(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJH201607019.htm
[8]	PARK B, SHIN T S, CHO J S, et al. Characterizing hyperspectral microscope imagery for classification of blueberry firmness with deep learning methods[J]. Agronomy, 2021, 12(1): 85. DOI: 10.3390/agronomy12010085
[9]	QIAO M, XU Y, XIA G, et al. Determination of hardness for maize kernels based on hyperspectral imaging[J]. Food Chemistry, 2021, 366(2): 130559.
[10]	马帅帅, 于慧春, 殷勇, 等. 黄瓜水分和硬度高光谱特征波长选择与预测模型构建[J]. 食品与机械, 2021, 37(2): 145-151. https://www.cnki.com.cn/Article/CJFDTOTAL-SPJX202102028.htm MA Sh Sh, YU H Ch, YIN Y, et al. Selection of hyperspectral characteristic wavelength and construction of prediction model for cucumber hardness and moisture[J]. Food & Machinery, 2021, 37(2): 145-151(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SPJX202102028.htm
[11]	ERKINBAEV Ch, DERKSEN K, PALIWAL J, et al. Single kernel wheat hardness estimation using near infrared hyperspectral imaging[J]. Infrared Physics and Technology, 2019, 98(6): 250-255.
[12]	SU J Y, YI D W, LIU C J, et al. Dimension reduction aided hyperspectral image classification with a small-sized training dataset: Experimental comparisons[J]. Sensors, 2017, 17(12): 2726. DOI: 10.3390/s17122726
[13]	XIONG J T, LIN R, BU R B, et al. A micro-damage detection method of litchi fruit using hyperspectral imaging technology[J]. Sensors, 2018, 18(3): 700. DOI: 10.3390/s18030700
[14]	WU D, MENG L W, YANG L, et al. Feasibility of laser-induced breakdown spectroscopy and hyperspectral imaging for rapid detection of thiophanate-methyl residue on mulberry fruit[J]. International Journal of Molecular Sciences, 2019, 20(8): 2017. DOI: 10.3390/ijms20082017
[15]	赵凡, 闫昭如, 宋海燕. 应用高光谱鉴别黑枸杞和唐古特白刺果[J]. 光谱学与光谱分析, 2021, 41(7): 2240-2244. https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN202107046.htm ZHAO F, YAN Zh R, SONG H Y. Hyperspectra used to recognize Black Goji berry and nitraria Tanggu[J]. Spectroscopy and Spectral Analysis, 2021, 41(7): 2240-2244(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN202107046.htm
[16]	北京市农林科学院林业果树研究所; 农业部果品及苗木质量监督检验测试中心. 水果硬度的测定: NY/T 2009-2011[S]. 北京: 中华人民共和国农业部, 2011: 1-5. BEIJING ACADEMY OF FORESTRY AND POMOLOGY SCIENCES, LABORATORY OF QUALITY & SAFETY RISK ASSESSMENT FOR FRUIT. Determination of fruit firmness: NY/T 2009-2011[S]. Beijing: Ministry of Agriculture of the PRC, 2011: 1-5(in Chinese).
[17]	姜一河, 王涛, 常红伟. 高光谱图像特征提取方法研究综述[J]. 电光与控制, 2020, 27(10): 73-77. https://www.cnki.com.cn/Article/CJFDTOTAL-DGKQ202010015.htm JIANG Y H, WANG T, CHANG H W. An overview of hyperspectral image feature extraction[J]. Electronics Optics & Control, 2020, 27(10): 73-77(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DGKQ202010015.htm
[18]	白丽敏, 李粉玲, 常庆瑞, 等. 结合SPA和PLS法提高冬小麦冠层全氮高光谱估算的精确度[J]. 植物营养与肥料学报, 2018, 24(5): 1178-1184. https://www.cnki.com.cn/Article/CJFDTOTAL-ZWYF201805006.htm BAI L M, LI F L, CHANG Q R, et al. Increasing accuracy of hyper-spectral remote sensing for total nitrogen of winter wheat canopy by use of SPA and PLS methods[J]. Journal of Plant Nutrition and Fertilizers, 2018, 24(5): 1178-1184(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZWYF201805006.htm
[19]	欧阳爱国, 万启明, 李雄, 等. 高光谱成像的水稻螟虫蛀入检测方法[J]. 光谱学与光谱分析, 2021, 41(12): 3844-3850. https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN202112037.htm OUYANG A G, WAN Q M, LI X, et al. Research on rich borer detection methods based on hyperspectral imaging technology[J]. Spectroscopy and Spectral Analysis, 2021, 41(12): 3844-3850(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN202112037.htm
[20]	FAN L L, ZHAO J L, XU X G, et al. Hyperspectral-based estimation of leaf nitrogen content in corn using optimal selection of multiple spectral variables[J]. Sensors, 2019, 19(13): 2898.
[21]	刘璐, 邵慧, 孙龙, 等. 利用高光谱激光雷达检测木材的霉变与含水量[J]. 激光技术, 2023, 47(5): 620-626. DOI: 10.7510/jgjs.issn.1001-3806.2023.05.007 LIU L, SHAO H, SUN L, et al. Detection of mildew and moisture content in timber by hyperspectral LiDAR[J]. Laser Technology, 2023, 47(5): 620-626(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2023.05.007
[22]	MARSHALL M, BELGIU M, BOSCHETTI M, et al. Field-level crop yield estimation with PRISMA and Sentinel-2[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 187(2): 191-210.
[23]	高升, 徐建华. 高光谱成像的红提总酸与硬度的预测及其分布可视化[J]. 食品科学, 2023, 44(2): 327-336. https://www.cnki.com.cn/Article/CJFDTOTAL-SPKX202302041.htm GAO Sh, XU J H. Hyperspectral imaging for prediction and distribution visualization of total acidity and hardness of red globe grapes[J]. Food Science, 2023, 44(2): 327-336(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SPKX202302041.htm
[24]	SAVAŞLI E, KARADUMAN Y, ÖNDER O, et al. Estimating technological quality parameters of bread wheat using sensor-based norma-lized difference vegetation index[J]. Journal of Cereal Science, 2022, 107(8): 103535.
[25]	QIN J, BAI H Y, ZHAO P, et al. Dendrochronology-based norma-lized difference vegetation index reconstruction in the Qinling Mountains, North-Central China[J]. Forests, 2022, 13(3): 443.
[26]	PAVLO L. Forecasting oil crops yields on the regional scale using normalized difference vegetation index[J]. Journal of Ecological Engineering, 2021, 22(3): 53-57.
[27]	PENG Y, FAN M, BAI L, et al. Identification of the best hyperspectral indices in estimating plant species richness in sandy grasslands[J]. Remote Sensing, 2019, 11(5): 558.

施引文献(4)

期刊类型引用(2)

1.	王卉，刘庆菊，栾云霞，贾文珅. 高光谱成像技术在草莓品质检测中的应用. 食品工业. 2025(01): 138-142 . 百度学术
2.	杨洋，徐熙平，薛航，张宁，张越，索科. 基于SPA-PSO-BP的花生高光谱图像分类方法研究. 激光技术. 2024(04): 556-564 . 本站查看

其他类型引用(2)

资源附件(0)

图(9) / 表(4)

计量

文章访问数: 9
HTML全文浏览量: 0
PDF下载量: 7
被引次数: 4

引言
1. 助降场景下紫外光通信模型
1.1 直升机助降引导模型
1.2 紫外光近直视通信模型
1.3 大气折射率结构常数
1.4 近直视通信链路强湍流信道模型
2. 系统误比特率性能分析
3. 3种分集合并方法误比特率性能分析
3.1 最大比合并方式
3.2 等增益合并方式
3.3 选择合并方式
4. 仿真分析和实验验证
5. 结论

引言
1. 助降场景下紫外光通信模型
1.1 直升机助降引导模型
1.2 紫外光近直视通信模型
1.3 大气折射率结构常数
1.4 近直视通信链路强湍流信道模型
2. 系统误比特率性能分析
3. 3种分集合并方法误比特率性能分析
3.1 最大比合并方式
3.2 等增益合并方式
3.3 选择合并方式
4. 仿真分析和实验验证
5. 结论

参考文献(27)

施引文献(4)

资源附件(0)

基于高光谱指数分割的草莓硬度预测与研究

通讯作者:
邵慧, shaohui@ahjzu.edu.cn

计量

Prediction and study of strawberry hardness based on hyperspectral index segmentation

引言

1. 助降场景下紫外光通信模型

1.1 直升机助降引导模型

1.2 紫外光近直视通信模型

1.3 大气折射率结构常数

1.4 近直视通信链路强湍流信道模型

2. 系统误比特率性能分析

3. 3种分集合并方法误比特率性能分析

3.1 最大比合并方式

3.2 等增益合并方式

3.3 选择合并方式

4. 仿真分析和实验验证

5. 结论

期刊类型引用(2)

其他类型引用(2)

计量

目录

引言

1. 助降场景下紫外光通信模型

1.1 直升机助降引导模型

1.2 紫外光近直视通信模型

1.3 大气折射率结构常数

1.4 近直视通信链路强湍流信道模型

2. 系统误比特率性能分析

3. 3种分集合并方法误比特率性能分析

3.1 最大比合并方式

3.2 等增益合并方式

3.3 选择合并方式

4. 仿真分析和实验验证

5. 结论

友情链接：

基于高光谱指数分割的草莓硬度预测与研究

通讯作者: 邵慧, shaohui@ahjzu.edu.cn

计量

出版历程

Prediction and study of strawberry hardness based on hyperspectral index segmentation

引言

1. 助降场景下紫外光通信模型

1.1 直升机助降引导模型

1.2 紫外光近直视通信模型

1.3 大气折射率结构常数

1.4 近直视通信链路强湍流信道模型

2. 系统误比特率性能分析

3. 3种分集合并方法误比特率性能分析

3.1 最大比合并方式

3.2 等增益合并方式

3.3 选择合并方式

4. 仿真分析和实验验证

5. 结论

期刊类型引用(2)

其他类型引用(2)

计量

出版历程

目录

引言

1. 助降场景下紫外光通信模型

1.1 直升机助降引导模型

1.2 紫外光近直视通信模型

1.3 大气折射率结构常数

1.4 近直视通信链路强湍流信道模型

2. 系统误比特率性能分析

3. 3种分集合并方法误比特率性能分析

3.1 最大比合并方式

3.2 等增益合并方式

3.3 选择合并方式

4. 仿真分析和实验验证

5. 结论

友情链接：

通讯作者:
邵慧, shaohui@ahjzu.edu.cn