Optical design of biprism 2-D scanning system for wind LiDAR
-
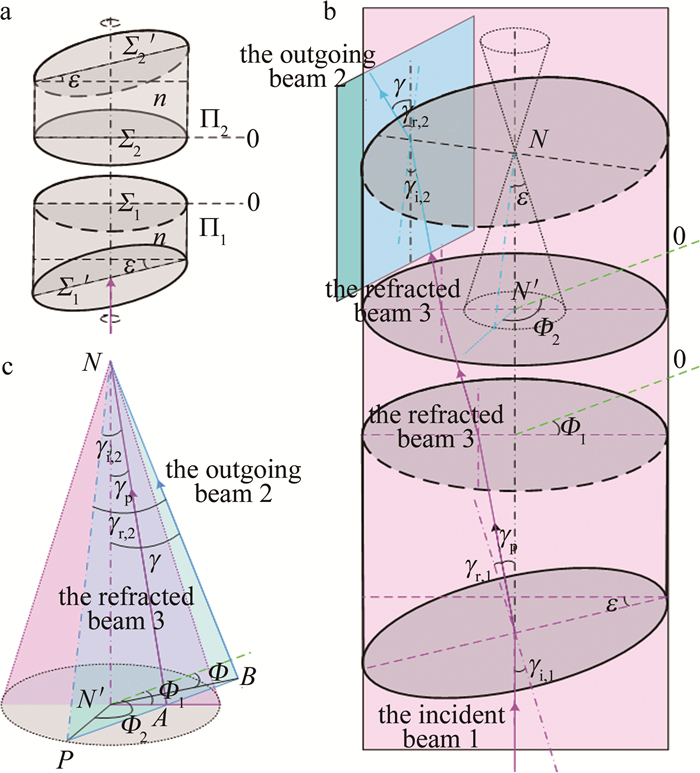
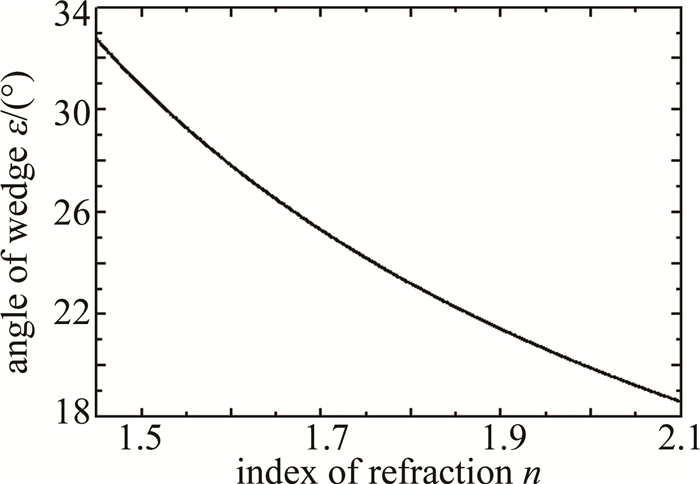
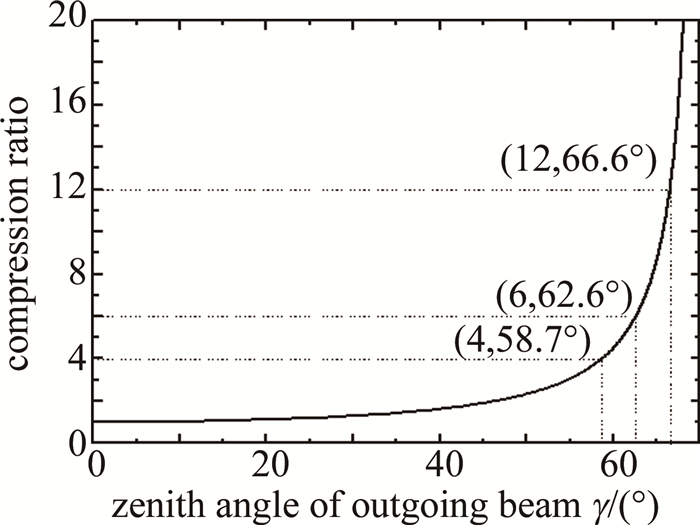
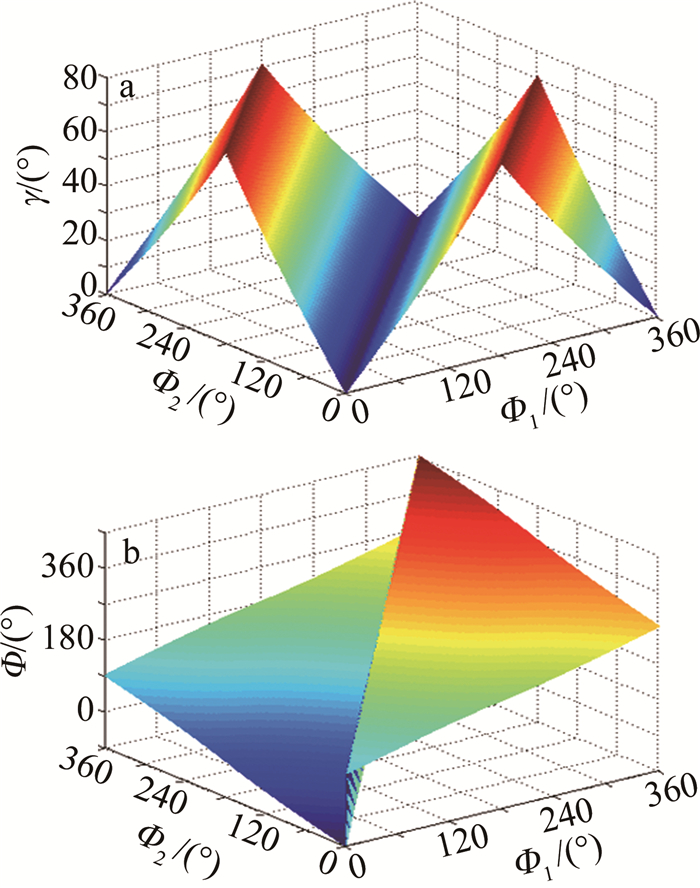
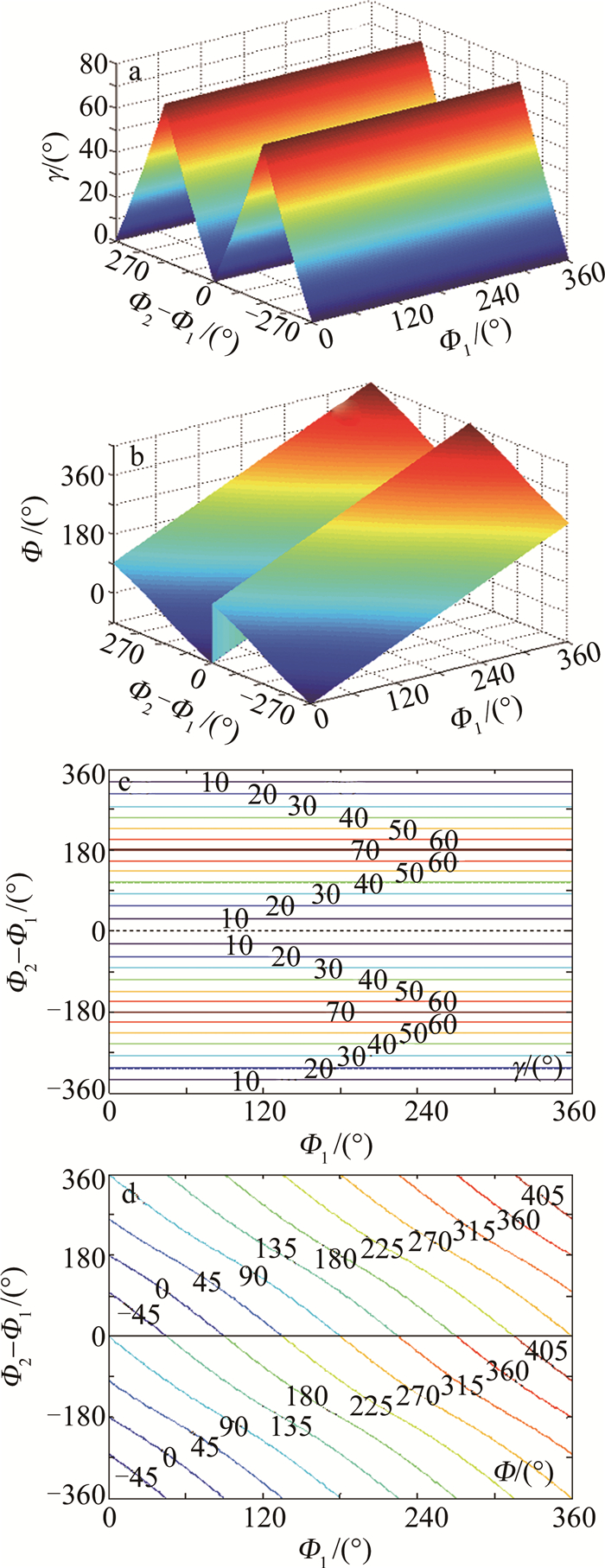
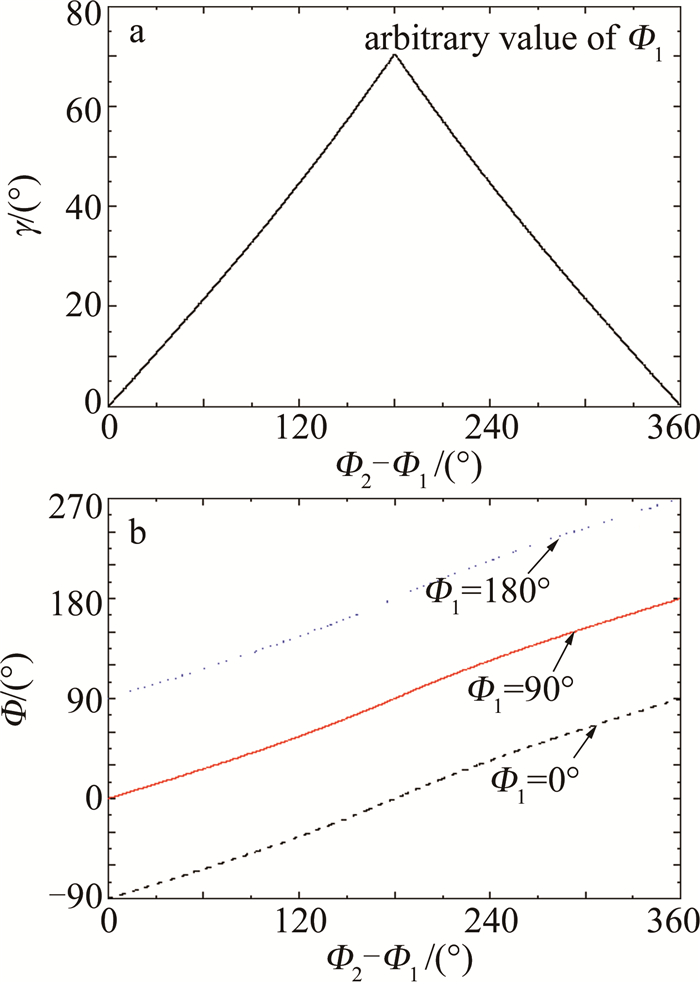
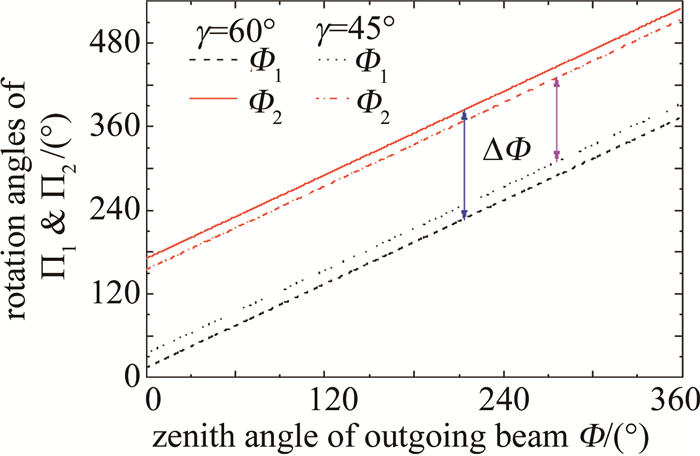
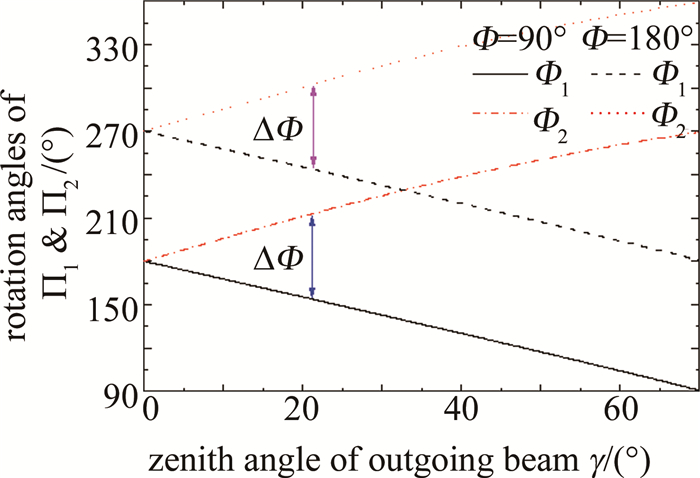
摘要: 传统的测风激光雷达双反射镜式2维扫描系统体积较大、结构相对复杂, 不利于系统小型一体化集成。基于旋转双圆楔形棱镜, 研究了新型2维光学扫描系统; 分析了系统的工作原理, 推导出了双圆楔形棱镜的旋转角与出射光束方位角及天顶角之间的简单正反向函数关系式, 对楔形棱镜的折射率和楔角进行了优化选取和设计。结果表明, 当工作波长为532 nm、楔形棱镜材料折射率为2.03时, 最优设计楔角为19.5°; 出射光束最大天顶角不仅取决于楔形棱镜折射率和楔角, 还受光束压缩效应的制约。该系统结构紧凑、便于集成, 能实现出射光束大范围和快速高精度的扫描, 也能实现测风激光雷达以平面位置显示、距离高度显示等光束扫描模式工作。Abstract: 2-D scanning system with double mirrors of a traditional wind light detection and ranging(LiDAR) was large in volume and complex in structure, which was not conducive to the small-scale integration of the system. A new 2-D optical scanning system based on rotating double circular wedge prism was studied. The working principle of the system was analyzed, and the simple forward and inverse functional relationship between the rotation angle of the double circular wedge prism and the azimuth and zenith angle of the outgoing beam was derived. The refractive index and wedge angle of the wedge prism were optimized and designed. The results show that when the working wavelength is 532 nm and the refractive index of wedge prism material is 2.03, the optimal wedge angle is 19.5°. The maximum zenith angle of the outgoing beam depends not only on the refractive index and wedge angle of the wedge prism, but also on the beam compression effect. The system is compact and easy to integrate, and large-scale, fast and high-precision scanning of the outgoing beam can be realized. The wind LiDAR can also work in beam scanning modes such as plane position display and distance height display.
-
-
![]()
图 1 基于旋转双圆楔形棱镜的光束2维扫描系统结构
Figure 1. Structure of 2-D beam scanning system based on double rotating round wedge prisms
![]()
图 2 旋转双圆楔形棱镜中光束传播轨迹及其简化模型
Figure 2. Beam propagation trajectory and its simplified model in double rotating round wedge prisms
![]()
图 3 临界全反射条件下，棱镜楔角随折射率的变化曲线
Figure 3. Curve of prism wedge angle with refractive index under critical condition of total internal reflection
![]()
图 4 光束压缩比随出射光束天顶角的变化曲线
Figure 4. Curve of beam compression ratio with zenith angle of outgoing beam
![]()
图 5 出射光束天顶角γ与方位角Φ随Π1和Π2的旋转角Φ1和Φ2变化3维图
Figure 5. 3-D diagram of zenith angle γ and azimuth angle Φ of outgoing beam with rotation angles Φ1 and Φ2 of Π1 and Π2
![]()
图 6 出射光束天顶角γ与方位角Φ随Φ1及两棱镜的旋转角度差Φ2-Φ1变化图
Figure 6. Variation of zenith angle γ and azimuth angle Φ of outgoing beam with rotation angle Φ1 and rotation angle difference between two prisms Φ2-Φ1
![]()
图 7 出射光束天顶角γ与方位角Φ随两棱镜的旋转角度差Φ2-Φ1的变化曲线
Figure 7. Curve of zenith angle γ and azimuth angle Φ of outgoing beam with Φ2-Φ1
![]()
图 8 PPI扫描模式下，不同天顶角γ时，旋转角Φ1、Φ2和方位角Φ的对应变化关系
Figure 8. Variation of rotation angles Φ1 and Φ2 with azimuth angle Φ under different elevation angles γ in PPI mode
-
[1] 沈法华, 蒋佳佳, 周慧. 一种基于单轴旋转双圆楔形棱镜的便携式激光雷达二维扫描系统及扫描方法: 中国, CN202210034312.9[P]. 2022-07-15. SHEN F H, JIANG J J, ZHOU H. A portable lidar two-dimensional scanning system and scanning method based on a single axis rotating bicircular wedge prism: CN202210034312.9[P]. 2022-07-15(in Chinese).
[2] 朱峻可, 李丽娟, 林雪竹. 激光雷达测量系统的测量场规划研究[J]. 激光技术, 2021, 251(1): 99-104. DOI: 10.7510/jgjs.issn.1001-3806.2021.01.017 ZHU J K, LI L J, LIN X Zh. Research on the measurement field planning of lidar measurement system[J]. Laser Technology, 2021, 45(1): 99-104(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2021.01.017
[3] 梁晓峰, 张振华. 浅析舰船激光测风雷达技术应用及发展趋势[J]. 激光技术, 2021, 45(6): 768-775. DOI: 10.7510/jgjs.issn.1001-3806.2021.06.016 LIANG X F, ZHANG Zh H. Application and development trend of shipborne wind lidar[J]. Laser Technology, 2021, 45(6): 768-775(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2021.06.016
[4] LU S, GAO M, YANG Y, et al. Inter-satellite laser communication system based on double Risley prisms beam steering[J]. Applied Optics, 2019, 58(27): 7517-7522. DOI: 10.1364/AO.58.007517
[5] 范大鹏, 周远, 鲁亚飞, 等. 旋转双棱镜光束指向控制技术综述[J]. 中国光学, 2013, 6(2): 136-150. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGA201302003.htm FAN D P, ZHOU Y, LU Y F, et al. A review of pointing control techniques for rotating biprism beams[J]. Chinese Optics, 2013, 6(2): 136-150(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGA201302003.htm
[6] 高飞, 王苗. 双光楔光轴指向调整技术[J]. 光电工程, 2018, 45(11): 60-66. https://www.cnki.com.cn/Article/CJFDTOTAL-GDGC201811007.htm GAO F, WANG M. Double optical wedge axis pointing adjustment technology[J]. Opto-Electronic Engineering, 2018, 45(11): 60-66(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDGC201811007.htm
[7] YANG Y. Analytic solution of free space optical beam steering using Risley prisms[J]. Journal of Lightwave Technology, 2008, 26(21): 3576-3583. DOI: 10.1109/JLT.2008.917323
[8] LIU L R, LUAN Z, WANG L, et al. Large-optics white light interferometer for laser wavefront test: Apparatus and application[J]. Proceedings of the SPIE, 2008, 7091: 70910Q. DOI: 10.1117/12.793515
[9] LIU L R, WANG L, LUAN Z, et al. The mechanical design of the large-optics double-shearing interferometer for the test of the diffraction-limited wave front[J]. Proceedings of the SPIE, 2008, 7091: 70910S. DOI: 10.1117/12.793954
[10] SUN J, LIU L, YUN M, et al. The effect of the rotating double-prism wide-angle laser beam scanner on the beam shape[J]. International Journal for Light and Electron Optics, 2005, 116(12): 553-556. DOI: 10.1016/j.ijleo.2005.01.040
[11] 韦中超, 熊言威, 莫玮, 等. 旋转双光楔折射特性与二维扫描轨迹的分析[J]. 应用光学, 2009, 30(6): 939-943. DOI: 10.3969/j.issn.1002-2082.2009.06.011 WEI Zh Ch, XIONG Y W, MO W, et al. Analysis of refraction characteristics and two-dimensional scanning trajectory of rotating double optical wedge[J]. Journal of Applied Optics, 2009, 30(6): 939-943(in Chinese). DOI: 10.3969/j.issn.1002-2082.2009.06.011
[12] LI Y. Closed form analytical inverse solutions for Risley prism based beam steering systems in different configurations[J]. Applied Optics, 2011, 50(22): 4302-4309.
[13] ALEXANDRU S, MARIUS T, VIRGIL-FLORIN D, et al. Modeling of Risley prisms devices for exact scan patterns[J]. Proceedings of the SPIE, 2013, 8789: 878912.
[14] 周远, 鲁亚飞, 黑沫, 等. 旋转双棱镜光束指向解析解[J]. 光学精密工程, 2013, 21(6): 1373-1379. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201306002.htm ZHOU Y, LU Y F, HEI M, et al. The rotating biprism beam points to the analytical solution[J]. Optical and Precision Engineering, 2013, 21(6): 1373-1379(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201306002.htm
[15] 周远, 鲁亚飞, 黑沫, 等. 旋转双棱镜光束指向的反向解析解[J]. 光学精密工程, 2013, 21(7): 1693-1700. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201307008.htm ZHOU Y, LU Y F, HEI M, et al. Inverse analytical solution of rotating biprism beam pointing[J]. Optical and Precision Engineering, 2013, 21(7): 1693-1700(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM201307008.htm
[16] 张鲁薇, 王卫兵, 王锐, 等. 基于正解过程的Risley棱镜光束指向控制精度分析[J]. 中国光学, 2017, 10(4): 507-513. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGA201704014.htm ZHANG L W, WANG W B, WANG R, et al. Analysis of beam pointing control precision of Risley prism based on forward solution process[J]. Chinese Optics, 2017, 10(4): 507-513(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGA201704014.htm
[17] 李锦英, 陈科, 彭起, 等. 旋转双棱镜大范围快速高精度扫描技术[J]. 光电技术应用, 2020, 35(2): 44-48. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYG202002009.htm LI J Y, CHEN K, PENG Q, et al. Rotating double prism scanning technology with large range and high accuracy[J]. Electro-Optic Technology Application, 2020, 35(2): 44-48(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GDYG202002009.htm
[18] 周远, 陈英, 蒋国保, 等. 旋转双棱镜目标跟踪的非线性问题分析[J]. 光学学报, 2021, 41(18): 1823002. https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB202118026.htm ZHOU Y, CHEN Y, JIANG G B, et al. Nonlinear problem analysis of rotating biprism target tracking[J]. Acta Optica Sinica, 2021, 41(18): 1823002(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB202118026.htm
下载:
计量
- 文章访问数: 11
- HTML全文浏览量: 2
- PDF下载量: 6