Automatic positioning of optical axis of wave-plate in a laser feedback birefringence measurement system
-
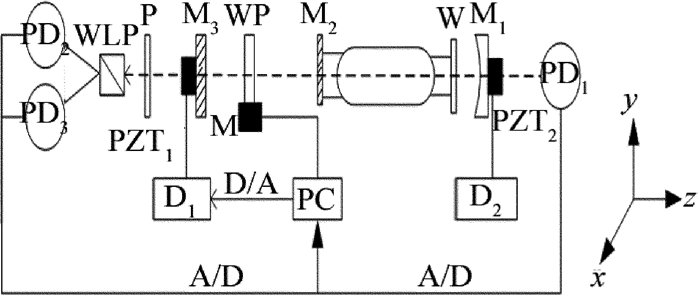
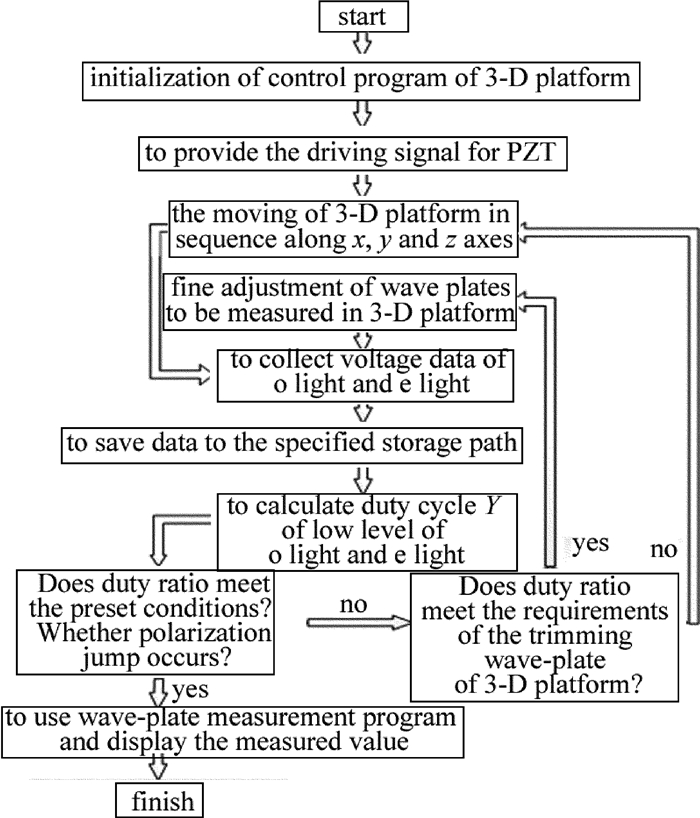
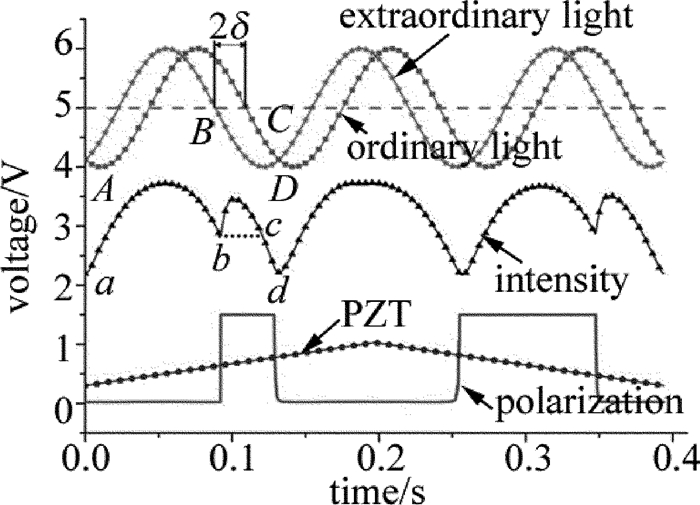
摘要: 为了解决传统双折射测量系统在调节光学元件的过程中,结构复杂、耗时长且不状态稳定的问题,采用计算偏振跳变曲线中o光和e光低电平占空比的方法,增加了自动旋转波片的功能,优化出一套具有较高工作效率的双折射测量系统。该系统可自动调整波片快轴方向,使其可对准激光器的本征偏振方向,减少了人为判断波片快轴时可能引入的测量误差。结果表明,波片相位延迟的最大偏差为0.65°,标准差降低28%。双折射测量系统的测量精度及稳定性满足工业化生产的要求。Abstract: In order to solve the problem of complex structure, time-consuming and unstable state in the process of adjusting optical elements in a traditional birefringence measurement system, the duty cycles of o light and e light at low levels in polarization flipping curves were calculated.The function of automatic rotating wave-plate was added in a birefringence measurement system optimized with high efficiency.The system can automatically adjust the direction of fast axis of the wave-plate aligned with the intrinsic polarization direction of laser and reduce the measurement error that may be introduced when judging the fast axis of wave-plate artificially.After many measurements, the results show that the maximum deviation of wave-plate phase delay is 0.65°, and the standard deviation is reduced by 28%.The measurement accuracy and stability of birefringence measurement systems have met the requirements of industrial production.
-
-
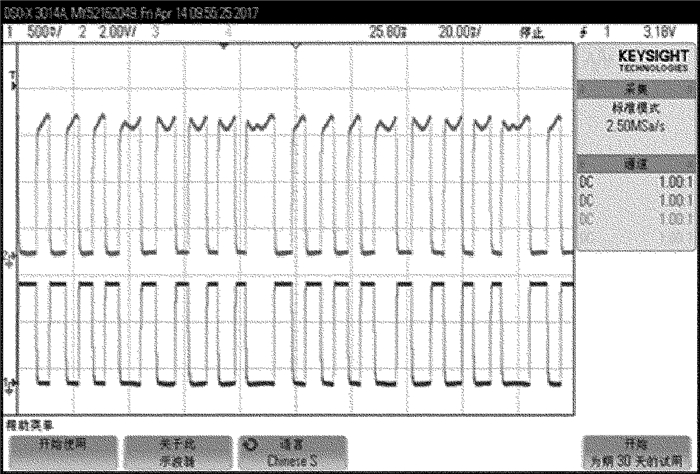
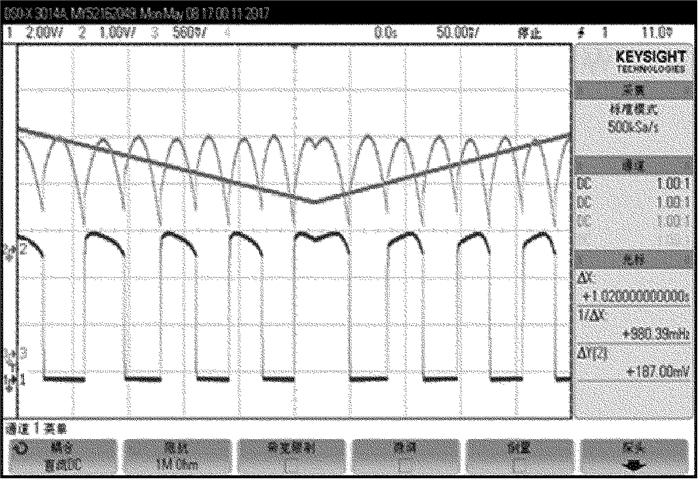
Table 1 Analysis of duty cycle of the low level of ordinary light and extraordinary light
experiment times the traditional way of
adjusting wave-platethe optimized mode of
adjusting wave-plate1 0.4653 0.4762 2 0.4655 0.4715 3 0.4685 0.4823 4 0.4547 0.4712 5 0.4667 0.4695 6 0.4675 0.4757 7 0.4695 0.4707 8 0.4515 0.4837 9 0.4682 0.4722 10 0.4705 0.4812 average 0.4648 0.4754 standard deviation 0.0064 0.0053 Table 2 Analysis of the measured value of phase retardation of λ/4 wave-plate
experiment
timesthe measured value of
the wave-plate before
the system is optimized/(°)the measured value
of the wave-plate after
the system is optimized/(°)1 89.12 89.66 2 89.25 90.07 3 88.77 89.44 4 89.04 89.54 5 89.23 89.77 6 89.07 89.37 7 89.33 89.75 8 88.47 89.90 9 89.42 89.35 10 89.63 89.58 average 89.11 89.64 standard
deviation0.3103 0.2219 -
[1] FEI L, ZHANG S, LI Y, et al. Polarization control in a He-Ne laser using birefringence feedback[J]. Optics Express, 2005, 13(8):3117-3122. DOI: 10.1364-OPEX.13.003117/
[2] GUO B, ZHU K, ZHANG S, et al. Single-spot two-dimensional displacement measurement based on self-mixing interferometry[J]. Optica, 2017, 4(7):729-732. http://cn.bing.com/academic/profile?id=f61c43fbde1a7ecc76e54a23b52f8a27&encoded=0&v=paper_preview&mkt=zh-cn
[3] LI H H, ZHANG Sh L, TAN Y D, et al. Wave plate phase retardation measurement on contact block based on optical feedback[J]. Journal of Applied Optics, 2011, 32(5):1004-1008(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-YYGX201105039.htm
[4] CUI L, ZHANG Sh L. Semi-classical theory model for feedback effect of orthogonally polarized dual frequency He-Ne laser[J]. Optics Express, 2005, 13(17):6558-6563. http://cn.bing.com/academic/profile?id=7bb535e1804f430227052b3d349d4554&encoded=0&v=paper_preview&mkt=zh-cn
[5] LIU M, ZHANG Sh L, LIU W X, et al. Error source and its elimination in phase retardation measurement of wave plate based on laser feedback[J]. Journal of Applied Optics, 2008, 29(6):961-966(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-YYGX200806030.htm
[6] TAN Y D, ZHANG Sh L. Orthogonally linearly polarized dual frequency Nd:YAG lasers with tunable frequency difference and its application in precision angle measurement[J]. Chinese Physics Letters, 2007, 24(9):2590-2593. http://cn.bing.com/academic/profile?id=1e8a56ee9ff7dadb7719e04c3f94d7a7&encoded=0&v=paper_preview&mkt=zh-cn
[7] WU Y, TAN Y D, ZHANG Sh L, et al. Polarization characteristics of He-Ne laser with different directions of polarized feedback[J]. Applied Optics, 2013, 52(22):5371-5375. http://cn.bing.com/academic/profile?id=dc96e3f668cbe720f475db03b612fdd3&encoded=0&v=paper_preview&mkt=zh-cn
[8] WU Y, TAN Y D, ZENG Z, et al. Note:High-performance He-Ne laser feedback interferometer with birefringence feedback cavity scanned by piezoelectric transducer[J]. Review of Scientific Instruments, 2013, 84(5):180-184. http://d.old.wanfangdata.com.cn/Periodical/yckj201606013
[9] ZENG M, DING J X. Polarization characteristics of external cavity He-Ne lasers[J]. Laser Technology, 1992, 16(1):21-28(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS199201008.htm
[10] ZENG Z, QU X, TAN Y, et al. High-accuracy self-mixing interferometer based on single high-order orthogonally polarized feedback effects[J]. Optics Express, 2015, 23(13):16977-16983. http://cn.bing.com/academic/profile?id=e4b596bab84971c10409f0131cbae00c&encoded=0&v=paper_preview&mkt=zh-cn
[11] WEI Zh M, YANG K Y. Controller of multi-axis motorized optical stages based on DAQ card and multiplexer[J].Laser Journal, 2010, 31(5):38-39(in Chinese). http://cn.bing.com/academic/profile?id=999074267b8e586715c3f97034372be5&encoded=0&v=paper_preview&mkt=zh-cn
[12] WANG L, LI G H, KONG Ch, et al. Phase retardation measurement with two λ/4 wave-plates[J]. Laser Technology, 2007, 31(6):663-664(in Chinese). http://en.cnki.com.cn/article_en/cjfdtotal-jgjs200706031.htm
[13] XU L, ZHANG Sh L, TAN Y D, et al. Simultaneous measurement of refractive-index and thickness for optical materials by laser feedback interferometry[J]. Review of Scientific Instruments, 2014, 85(8):1693-1697. http://cn.bing.com/academic/profile?id=e3e0636cf75d6450bf065ec02871c872&encoded=0&v=paper_preview&mkt=zh-cn
[14] LIN Y H, QU X Sh, WANG D G, et al. Research on measurement system for phase retardation for wave plates based on auto data acquisition[J]. Measurement & Control Technology, 2010, 29(6):41-44(in Chinese).
[15] WAN L Y, SUN J F, LIU L R, et al. Effects of optical axis deviation of wave-plates on the amplitude and phase of beams separated by a polarizing splitter[J]. Optical Technique, 2010, 36(2):307-310(in Chinese).
[16] ZHANG J, LI G H. The theory of correcting the retardation devation of a wave-plate[J]. Laser Technology, 2006, 30(3):274-276(in Chinese).
[17] SUO G G, WANG X R, HUANG Z Q, et al. Test method for birefaingence of Fourier quarter-wave-plate.Laser Technology, 2016, 40(1):131-135(in Chinese).
[18] GAO A, KONG Y, XIA G, et al. Research of temperature insensitivity of uniaxial birefringence filters[J]. Laser Technology, 2016, 40(4):476-478(in Chinese).
[19] XU C, TAN Y, ZHANG S, et al. The structure measurement of micro-electro-mechanical system devices by the optical feedback tomography technology[J]. Applied Physics Letters, 2013, 102(22):3648-3704.
[20] ZHANG P, TAN Y D, LIU W X, et al. Methods for optical phase retardation measurement:a review[J]. Science China, 2013, 56(5):1155-1164.



 下载:
下载: