网站地图
下载:
-
在现代空战中，由于飞机隐身特性的要求以及防区外远程探测的需求，致使机载激光测距回波信号极其微弱，甚至淹没于噪声之中。噪声与接收系统灵敏度密切相关，接收灵敏度是激光测距方程的重要参量。以往文献中[1-7]多见对背景噪声、探测器散粒噪声、产生复合噪声、光子波动噪声、热噪声等的分离分析，缺少对激光测距噪声的系统分析，对激光测距接收探测电路最大允许输入噪声很难有具体指导作用。如何根据空中小目标最大测程的要求，分析激光接收电路的最大允许输入噪声，进而评估激光回波接收探测放大检出电路设计方案的可行性，是激光测距机系统设计的重要前提条件。
激光测距接收系统的总噪声包含背景光噪声、雪崩管探测模块噪声、主放大器电噪声以及信号处理电路引入的噪声，噪声与接收灵敏度及最大测程密切相关。文中首先对此进行了仿真分析；其次，根据空中小目标最大测程要求，通过激光测距方程，分析了所需最小探测灵敏度；而后，通过对回波频谱特性以及探测模块和放大器带宽的仿真分析，计算了回波信号的放大倍数，推算出了主放大器输出信号的大小；最后，依据高斯白噪声模型和主放大器输出信号值，得出了激光测距接收电路的最大允许输入噪声值。据此，设计电路并进行试验测试，验证了理论分析，为远程激光回波接收探测电路的设计奠定了理论和实践基础。
-
激光测距机接收系统主要由接收光学部件、雪崩管(avalanche photodiode, APD)探测模块、主放大器单元以及数字信号处理(digital signal processing, DSP)电路等组成，见图 1。其总噪声主要包括背景光噪声、雪崩管探测模块噪声、主放大器电噪声以及信号处理电路引入的噪声。图中, FPGA为现场可编程门阵列(field-programmable gate array), FIFO为先入先出(first in first out)队列，A/D为模/数(analogue/digital)转换器。
Figure 1. Block diagram of laser ranging receiving system
-
背景光主要包含目标对太阳光的反射、大气的散射以及太阳光的直射[1]，总背景光功率Pb可表示如下：
$ \begin{array}{*{20}{c}} {{P_{\rm{b}}} = \frac{{\rm{ \mathsf{ π} }}}{{16}}{\eta _{\rm{r}}}\Delta \lambda \theta _{\rm{r}}^2D_{\rm{r}}^2\left[ {\rho {T_{\rm{a}}}{H_\lambda }\cos \theta \cos \varphi + } \right.}\\ {\left. {\frac{\beta }{{4\alpha }}\left( {1 - {T_{\rm{a}}}} \right){H_\lambda } + {\rm{ \mathsf{ π} }}{L_\lambda }} \right]} \end{array} $
(1) 式中，ηr为接收光学系统透过率，Δλ为窄带滤光片带宽，θr为接收视场角, Dr为接收系统有效通光直径，ρ为目标反射系数，Ta为大气透过率，Hλ为太阳光对地面的光谱辐射照度，θ为太阳射线和目标表面法线的夹角; φ为目标表面法线与接收光轴之间的夹角，β为大气散射系数，α为大气衰减系数，Lλ为太阳光的大气散射的光谱辐射亮度。为方便计算，简化模型，令α=1，β=1，cosθ=1，cosφ=1，并取ρ=0.2，ηr=0.6，Ta=0.87。其中，cosθ=1, cosφ=1，意味着太阳射线和目标表面法线的夹角是0°，目标表面法线与接收光轴之间的夹角也是0°，这种情况代表在空对空机载测距时，太阳射线、目标机法线以及载机测距机接收光轴共轴，且载机接收光学系统处于太阳射线与目标机中间，目标机法线正向对准太阳射线，载机接收光学系统正向对准目标机法线方向，此时，载机接收光学系统接收的目标机反射的背景光为最大值，cosθ=1, cosφ=1，是对背景光理论分析时较苛刻的假设。对于α=1和β=1这个假设条件的依据见参考文献[8]，对于1064nm波段，不同海拔、不同纬度、不同季节条件，大气衰减系数α与大气散射系数β的取值不同，文中α=1和β=1是综合上述3种条件，并结合文中最大测程Rmax=65km要求，取的一个较简化的模型。
(1) 式可简化如下：
$ \begin{array}{*{20}{c}} {{P_{\rm{b}}} = \frac{{\rm{ \mathsf{ π} }}}{{16}}{\eta _{\rm{r}}}\Delta \lambda \theta _{\rm{r}}^2D_{\rm{r}}^2\left[ {\rho {T_{\rm{a}}}{H_\lambda } + } \right.}\\ {\left. {\frac{1}{4}\left( {1 - {T_{\rm{a}}}} \right){H_\lambda } + {\rm{ \mathsf{ π} }}{L_\lambda }} \right]} \end{array} $
(2) $ {P_{\rm{b}}} \propto \left( {{\eta _{\rm{r}}}\Delta \lambda \theta _{\rm{r}}^2D_{\rm{r}}^2} \right) \times \left( {\rho {T_{\rm{a}}}} \right) $
(3) 可见，背景噪声光功率与测距机接收系统参量呈正相关，与大气及目标特性呈正相关。采用MODTRAN4.0软件对太阳光谱辐射亮度Lλ、太阳光谱辐射照度Hλ进行仿真，仿真结果见图 2和图 3。
Figure 2. Simulation of radiant luminance of sun light
Figure 3. Simulation of radiant illumination of sun light
由仿真结果可知，在1064nm波段，太阳光的大气散射的光谱辐射亮度Lλ=3.04×10-6W/(cm2·sr·nm), 太阳光对地面的光谱辐射照度Hλ=6.5×10-5W/ (cm2·nm)。
激光测距机接收系统以及大气和目标的参量选取分别为:背景噪声光功率Pb=2.7nW, ηr=0.6, Δλ=5nm, θr=1.0mrad, Dr=0.14m, Ta=0.84, ρ=0.2。
-
雪崩管探测模块由雪崩管探测器及前置放大器组成，其噪声模型如图 4所示[2]。图中, OPA为运算放大器(operation anplifier)。
Figure 4. Noise model of APD detection unit
总噪声包括四部分：雪崩管噪声、跨阻热噪声, 前置放大器等效电流噪声、前置放大器等效电压噪声。总噪声表示如下[2]：
$ I_{\rm{n}}^2 = I_{{\rm{APD}}}^2 + 2q{I_{{\rm{AMP}}}} + {\left( {{V_{{\rm{AMP}}}}{\omega _{{\rm{AMP}}}}C} \right)^2} + \frac{{4kT}}{{{R_{{\rm{AMP}}}}}} $
(4) 式中, In为总噪声电流，IAPD是雪崩管噪声电流，q是电子电荷，IAMP是前置放大器等效输入噪声电流，VAMP是放大器等效输入噪声电压，ωAMP是前置放大器的截止带宽，C是总等效输入电容，k是玻尔兹曼常数，T是温度，RAMP是前置放大器的跨阻。雪崩管噪声电流进一步用McIntyre等式表示：
$ {I_{{\rm{APD}}}} = \sqrt {2q\left[ {{I_{\rm{s}}} + \left( {{I_{\rm{b}}} + {I_{{\rm{PD}}}}} \right){M^2}F} \right]} $
(5) $ {I_{{\rm{PD}}}} = P{R_M} $
(6) 式中, Is是面暗电流，Ib是体暗电流，IPD为光电流，M是倍增因子，F是过剩噪声因子，P是入射光功率，RM为单位倍增因子条件下光谱响应度。雪崩管的面暗电流Is、体暗电流Ib由Arrhenius等式表示：
$ I\left( T \right) = {I_{{\rm{ref}}}}\exp \left[ {{E_{\rm{a}}}\left( {\frac{q}{k}} \right)\left( {\frac{1}{{{T_{{\rm{ref}}}}}} - \frac{1}{T}} \right)} \right] $
(7) 式中, Ea是电子势能，Tref是参考温度，Iref是参考温度所对应的噪声电流。雪崩倍增因子M表示如下：
$ M = \frac{K}{{{{\left( {{V_{\rm{b}}} - {V_{\rm{o}}}} \right)}^n}}} $
(8) 式中, Vb是雪崩击穿电压，Vo是雪崩偏压，K是与雪崩管探测器相关的常数, n为指数。
本文中雪崩管探测模块型号为LLAM-1060-R8BH，其-3dB带宽为200MHz，噪声等效功率谱密度为50fW/$\sqrt{\text{Hz}}$。
-
定义放大器的噪声系数Fn为放大器的输入功率信噪比与输出功率信噪比之比[1]，Fn值越大，放大器性能越坏。
$ {F_{\rm{n}}} = \frac{{{S_{\rm{i}}}/{N_{\rm{i}}}}}{{{S_{\rm{o}}}/{N_{\rm{o}}}}} $
(9) 式中，Si代表输入信号功率，Ni代表输入噪声功率，So代表输出信号功率，No代表输出噪声功率。
多级级联放大器的噪声系数表示如下[1]：
$ \begin{array}{*{20}{c}} {{F_{\rm{n}}} = {F_{{\rm{n,1}}}} + \frac{{{F_{{\rm{n,2}}}} - 1}}{{{K_{{\rm{g}},1}}}} + \frac{{{F_{{\rm{n,3}}}} - 1}}{{{K_{{\rm{g}},1}} \times {K_{{\rm{g}},2}}}} + }\\ { \cdots + \frac{{{F_{{\rm{n}},m}} - 1}}{{{K_{{\rm{g}},1}} \times {K_{{\rm{g}},1}} \times \cdots \times {K_{{\rm{g}},m - 1}}}}} \end{array} $
(10) 式中，Kg为放大器电压增益平方。可见，当前级的Kg较大时，后级放大器的的噪声系数相对于前级的一般可忽略，采用内置前置放大器且具有内增益的APD模块，后级主放大器的噪声可以忽略不计。
由上述噪声分析可以得出，激光测距接收系统的噪声主要由背景光噪声及雪崩管探测模块噪声两部分组成。接收系统的噪声直接影响到激光测距的探测灵敏度，最终决定激光测距机的最大测程，欲分析激光测距系统的最大允许输入噪声，应从测距方程分析着手。
-
最大输入噪声与接收灵敏度紧密相关，而接收灵敏度是激光测距方程的重要参量，直接影响到激光测距机的最大测程，故而欲分析最大测程与最大允许输入噪声的关系，应先分析测距方程。空中小目标激光测距方程表示如下：
$ {R_{\rm{s}}} = \left( {\frac{{{E_{\rm{t}}}{T_{\rm{t}}}}}{{\tau \theta _{\rm{t}}^2}}} \right) \times \left( {\frac{{D_{\rm{r}}^2{T_{\rm{r}}}}}{{{\rm{ \mathsf{ π} }}{P_{\rm{r}}}}}} \right) \times \left( {{A_{\rm{s}}}\rho T_{\rm{a}}^2} \right) $
(11) 式中，各参量定义及取值如下：激光发射单脉冲能量Et=200mJ, 激光脉冲宽度τ=10ns, 发射系统透过率Tt=0.9, 激光发散角θt=0.45mrad, 接收系统透过率Tr=0.6, 接收系统有效通光直径Dr=0.14m, 小目标面积Ac=2m2, 目标反射系数ρ=0.2, 大气透过率Ta=0.84, 最大测程Rmax=65km对应的接收灵敏度Pr≤5.3nW。
由于采用脉冲激光测距体制，回波信号的放大倍数与脉冲宽度及探测器、放大器的带宽密切相关，在测距信息处理电路距离检出阈值信噪比为2: 1(噪声为均方根值)的情况下，欲根据空中小目标最大测程对应的最小探测灵敏度，评估激光接收系统的最大允许输入噪声，需分析回波信号的频谱特型及探测器、放大器带宽特性。
-
在机载激光测距系统中，发射高斯激光脉冲宽度半峰全宽为(10±5)ns，由于目标及大气对发射光波的作用，回波采用钟形脉冲函数模型表示，回波脉宽半峰全宽按10ns计算。
钟形脉冲函数可表示如下：
$ f\left( t \right) = \alpha '\exp \left( { - \beta '{t^2}} \right) $
(12) 式中，α′和β′为系数常量，t代表时间，其中β′>0。钟形脉冲函数的傅里叶变换可表示如下：
$ F\left( \omega \right) = \sqrt {\frac{{\rm{ \mathsf{ π} }}}{{\beta '}}} \alpha '\exp \left( { - \frac{{{\omega ^2}}}{{4\beta '}}} \right) $
(13) 式中，ω代表角频率，ω=πf，f代表频率。类比(12)式和(13)式，在t=6ns处，f(6ns)对应的钟形函数可表示为:
$ f\left( t \right) = \alpha '\exp \left[ { - {{\left( {\frac{t}{6}} \right)}^2}} \right] $
(14) 式中，时间的单位为ns，由(14)式可计算回波脉宽半峰全宽为10ns。(14)式的傅里叶变换函数可表示如下：
$ \begin{array}{*{20}{c}} {F\left( f \right) = \sqrt {\frac{{\rm{ \mathsf{ π} }}}{{\beta '}}} \alpha '\exp \left[ { - {{\left( {\frac{\omega }{{333}}} \right)}^2}} \right] = }\\ {\beta '\exp \left[ { - {{\left( {\frac{\omega }{{333}}} \right)}^2}} \right] = \beta '\exp \left[ { - {{\left( {\frac{{{\rm{ \mathsf{ π} }}f}}{{333}}} \right)}^2}} \right]} \end{array} $
(15) 式中，频率f的单位为MHz。在傅里叶频域内，当f=150MHz，回波信号衰减为1/e2，脉宽为10ns的钟形函数傅里叶变换及频带信号比例仿真分析见图 5。
Figure 5. Frequency spectrum analysis of pulse signals
-
激光探测模块及主放大器应满足以下两点：探测模块-3dB带宽≥信号1/e2衰减对应带宽；主放大器-3dB带宽≥信号1/e2衰减对应带宽。
-
激光回波探测模块选择集成负指数热敏电阻、雪崩管探测器、前置放大器、热电制冷器于一体的制冷型探测模块LLAM-1060-R8BH，其主要参量如下：-3dB带宽为2.0×10-8MHz、光谱电压响应度为2.0×105kV/W, 噪声等效功率谱密度为5.0fW/$\sqrt{\text{Hz}}$，探测模块带宽大于信号1/e2衰减对应带宽[9-11]。
信号(10ns)1/e2衰减带宽(150MHz)对应的该探测模块噪声等效功率为0.61nW，依据最大测程Rmax=65km的要求，当激光回波信号强度为5.3nW时，计算制冷型探测模块输出信噪比为8.7: 1，大于阈值信噪比2: 1，且余量较多，可见，探测模块选型合理。
-
主放大器选择AD8367[12]，其-3dB带宽为500MHz，大于信号1/e2衰减对应带宽。由主放大器AD8367的增益伯德图及回波信号的频谱特性, 可得：
$ G = \frac{{\int_0^{f'} {\left[ {F'\left( \omega \right) \times G'\left( \omega \right)} \right]{\rm{d}}f} }}{{f'}} $
(16) 式中，G代表放大器平均放大倍数，F′(ω)代表回波信号频谱，G′(ω)代表放大器增益谱，f′代表带宽。对于脉宽为10ns的回波信号，在频谱带宽为100MHz时，可得平均放大倍数G=42.9。主放大器增益频谱曲线仿真见图 6。
Figure 6. Simulation of gain versus frequency of main amplifier
-
由上面的分析可知，激光测距接收系统的噪声主要由背景光噪声及雪崩管探测模块噪声两部分组成，其中，背景光功率Pb=2.7nW，探测模块噪声等效功率PAPD=0.61nW，两者之和Pn=3.3nW，且该值小于最大测程Rmax=65km对应的接收灵敏度光功率Pr=5.3nW，这两种噪声均按高斯白噪声模型分析。
高斯白噪声，其幅度分布服从高斯分布，功率谱密度服从均匀分布，即从频谱角度来说，频谱上任意时刻出现的噪声幅值都是随机的；从概率密度角度来说，高斯白噪声的幅值分布服从高斯分布。高斯白噪声的概率Y分布关系表示如下：
$ {Y_{ \pm 3\sigma }} = \int_{\bar X - 3\sigma }^{\bar X + 3\sigma } {\frac{1}{{\sigma \sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left[ { - \frac{{{{\left( {X - \bar X} \right)}^2}}}{{2{\sigma ^2}}}} \right]{\rm{d}}X} $
(17) 式中，X为噪声数学期望值，对于白噪声，其值为0;σ为噪声均方根值。可以计算，噪声因子大于3的概率为0.3%，由此可得，6倍于σ的高斯噪声峰峰值或3倍于σ的高斯噪声正向峰值，发生的概率为99.7%。高斯白噪声功率谱及幅值概率分布及幅值概率图仿真见图 7。图 7a中，横坐标代表频率，单位是Hz; 图 7b和图 7c中横纵坐标均无量纲。
Figure 7. Simulation of Gaussian noise
据上面所述小目标最大测程参量、探测模块参量、主放大器平均放大倍数以及高斯白噪声峰值与均方根值的关系，由下面两式可得激光测距接收电路输入噪声正向峰值Vp最大允许值为68mV，噪声峰峰值VPP最大允许值为136mV。据高斯噪声统计学理论，可以得出，在距离检出阈值信噪比为2: 1、激光测距接收电路输入噪声正向峰值Vp最大允许值为66mV、噪声峰峰值VPP最大允许值为136mV的前提下，空中小目标最大测程等于65km发生的概率可高达99.7%。
$ {V_{\rm{p}}} = 3{P_{\rm{r}}}{R_{\rm{v}}}G $
(18) $ {V_{{\rm{pp}}}} = 6{P_{\rm{r}}}{R_{\rm{v}}}G $
(19) 式中，Pr代表接收灵敏度光功率，取值为5.3nW; Rv代表电压响应度，取值为2.0×105V/W; G为放大器平均放大倍数, 取值为42.9。激光接收电路输入噪声分析中其它参量分别是:VAPD=1.06mV, 运算放大器噪声电压VOPA=45.5mV, 噪声均方根值为22.7mV。
-
依据上述回波信号频谱分析，探测模块、放大器选型，设计激光接收探测电路，测试主放大器输出端本底噪声，测试结果见图 8。从图中可以看出，噪声的峰峰值VPP最大值不大于136mV。将上述激光回波探测电路应用于机载激光测距系统中，采用消光比测试法，对近距离标定大目标测距。测试条件如下：大气能见度为7.5km；大目标标定距离Rb=4.2km；消光比衰减量N=46dB。
Figure 8. Test of output noise of amplifier
测试回波波形见图 9。图 9中，横坐标为时间信息，每点代表 5ns，纵坐标代表回波信号幅值，每点代表 5.86mV。此时，回波距离值稳定输出4.2km。由大目标测距方程:
$ {P_{\rm{r}}} = \frac{{{E_{\rm{t}}}{T_{\rm{t}}}{T_{\rm{r}}}D_{\rm{r}}^2\rho T_{\rm{a}}^2}}{{4R_{\rm{b}}^2\tau N}} $
(20) 
Figure 9. Test of echo wave signal of laser rangefinder
计算激光探测组件接收灵敏度达5.6nW。大目标消光比测距参量如下：激光发射单脉冲能量Et=200mJ；激光脉冲宽度τ=10ns；发射系统透过率Tt=0.9；接收系统透过率Tr=0.6；接收系统有效通光直径Dr=0.14m；目标反射系数ρ=0.4；大气透过率Ta=0.43。
测试表明，激光探测组件接收灵敏度光功率达5.6nW，与理论要求值5.3nW的偏差为5.7%。将实测灵敏度光功率5.6nW带入测距公式(11)式中，计算相对应的空中小目标的最大测程为64km，与理论要求值65km的偏差仅为1.5%。
-
阐述了接收电路最大允许输入噪声分析方法，设计了激光测距电路，通过消光比法对外场标定目标性能测试，给出了试验结果，印证了理论分析。试验表明，实测激光探测组件接收灵敏度与理论要求值的偏差为5.7%，消光比法折算空中小目标最大测程与理论要求值的偏差为1.5%，验证了接收电路最大输入噪声分析方法的正确性。在外场试飞过程中，发现对目标机迎头测试时，实测距离值与消光比法折算距离值存在不小于20%的偏差，在后续工作中，需对高斯噪声模型进行修正，这是由于激光测距接收系统噪声同时含有非均匀的周期性噪声。
机载远程激光测距机最大允许噪声仿真研究
Simulation and study on maximum permitted noise of airborne long-range laser range-finders
-
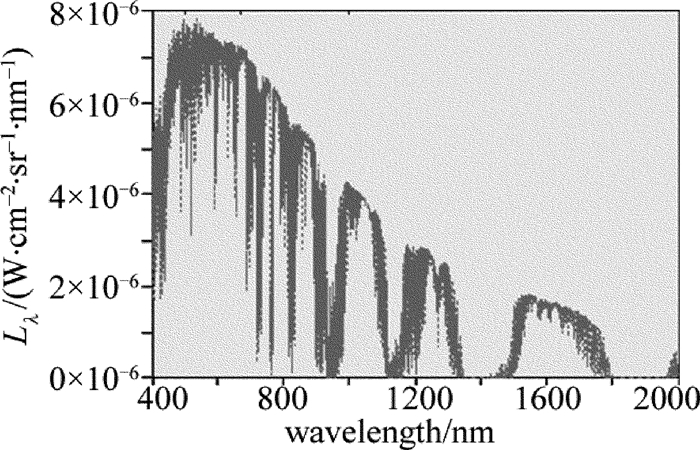
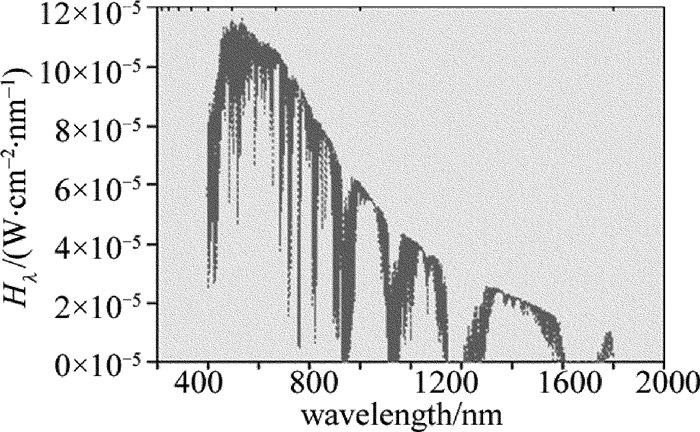
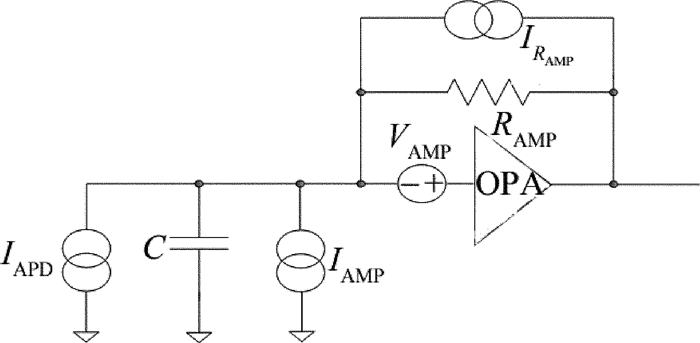
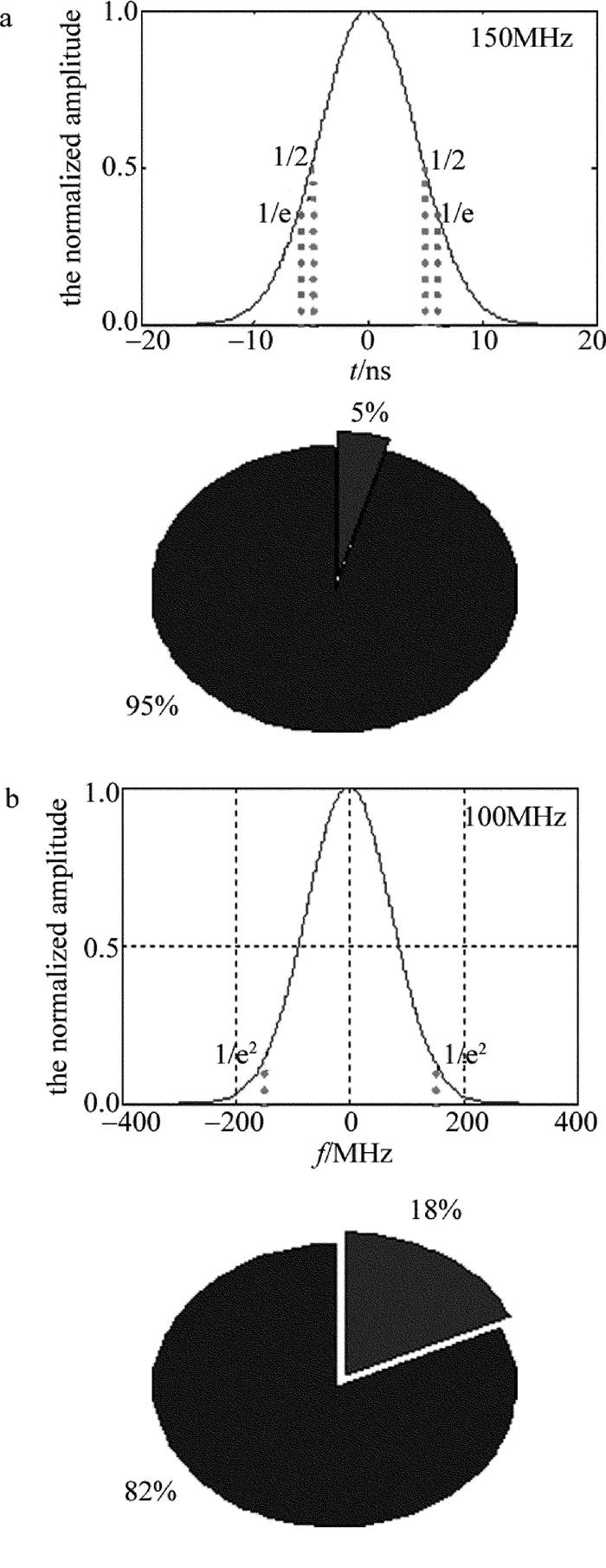
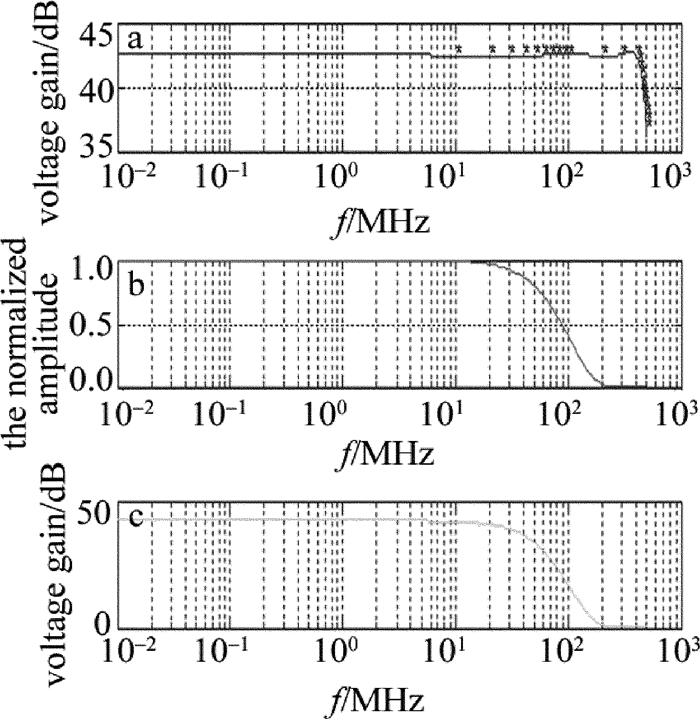
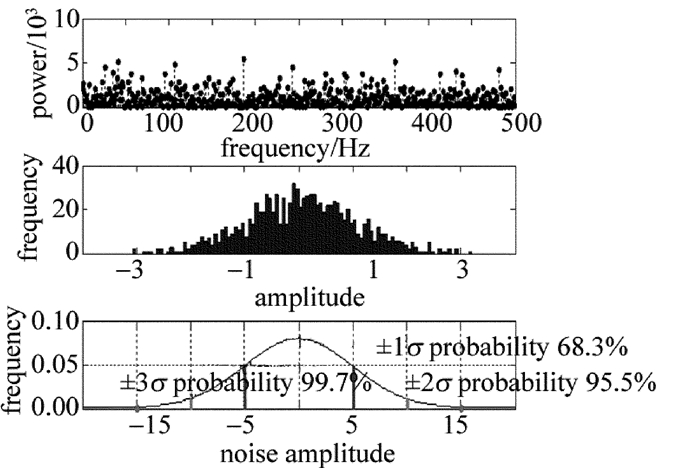
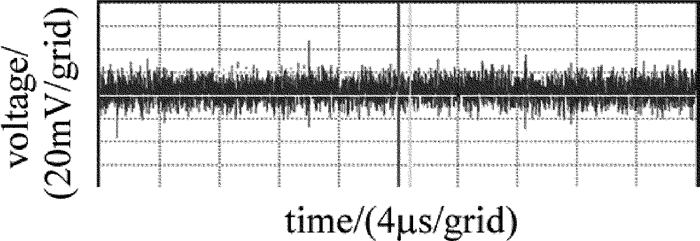
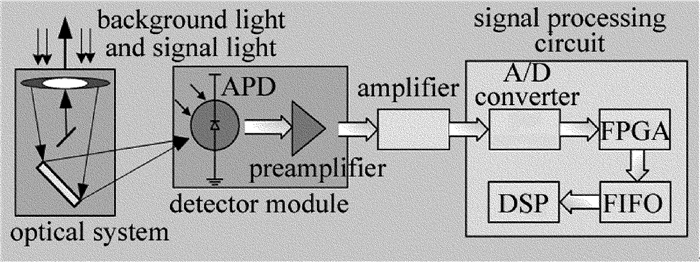
摘要: 为了提高机载远程激光测距机接收系统设计的可行性，从激光测距方程出发，分析了最小探测灵敏度与测程的关系。对回波频谱特性、探测模块带宽和放大器带宽进行了仿真，计算了回波信号的放大倍数，推算出主放大器输出信号的大小。依据高斯白噪声模型和主放大器输出信号值，推算了激光测距接收电路的最大允许输入噪声值。设计了电路并进行了试验测试。结果表明，激光接收灵敏度与理论值的偏差为5.7%，消光比法对应空中小目标最大测程与理论值的偏差仅为1.5%。该噪声分析方法对机载远程激光测距机的接收系统设计具有一定的指导意义。Abstract: In order to improve the design feasibility of receiving system for an airborne laser rangefinder, the maximum allowable input noise level was analyzed according to the parameters of the maximum range and signal-to-noise ratio threshold. Noise was closely related to the sensitivity of laser reception. Based on laser ranging equation, the relationship between the minimum detection sensitivity and detection range was analyzed. The characteristics of echo spectrum, the bandwidth of detection module and amplifier were simulated. The magnification of echo signal and the value of output signal of main amplifier were calculated. At the same time, according to Gaussian white noise model and output signal value of main amplifier, the maximum allowable input noise value of laser ranging receiving circuit was calculated. The circuit was designed and tested. The results show that the deviation between laser reception sensitivity and theoretical value is 5.7%. The deviation between the maximum value of extinction ratio method and the theoretical value is only 1.5%. The method of noise analysis has important guiding significance for the design of receiving system of airborne long-range laser range-finders.
-
Key words:
- laser technique /
- airborne laser ranging /
- noise /
- detection sensibility /
- frequency spectrum /
- bandwidth
-
Figure 6. Simulation of gain versus frequency of main amplifier
a—voltage gain b—the normalized amplitude c—simulation of voltage gain
-
[1] AN Y Y, ZENG X D. Photoelectricity detection principle[M]. Xi'an:Xidian University Publishing House, 2004:42-45(in Chinese). [2] FREDERIC L. Low noise optical receiver using Si APD[J].SPIE, 2009, 7212:523-534. [3] MA J L, FAN X T, YAN D K, et al. Design of laser range finding receiver circuit based on cooling-APD[J]. Infrared and Laser Engineering, 2013, 42(8):2041-2044(in Chinese). [4] GUO S, DING Q X, YAN Y. Noise suppression technologies used for avalanche photodiode[J].Electronics Optics & Control, 2012, 19(3):69-73(in Chinese). [5] FENG L L. Method of simulated testing of pulse laser rangefinder[J].Infrared and Laser Engineering, 2003, 32(2):127-129(in Chinese). [6] SUN Zh W, LIU Y J. Design of a new performance testing instrument of laser rangefinders[J]. Laser Technology, 2011, 35(6):792-794(in Chinese). [7] WU G X, DUAN F J, GUO H T. Optoelectronic heterodyne mixing and parameter optimization of avalance photodiodes[J].Laser Technology, 2015, 39(6):802-805(in Chinese). [8] LI J Zh. Handbook of optics(volume two)[M]. Xi'an:Shaanxi Science and Technology Press, 2010:1802(in Chinese). [9] EXCELITAS Co. A user guide-understanding avalanche photodiode for improving system performance[EB/OL].(2017-12-11).http://www.excelitas.com/downloads/app_avalanchephotodiodesusersguide.pdf. [10] PROKE S. Influence of temperature variation on optical receiver sensitivity and its compensation[J]. Radio Engineering, 2007, 16(3):13-18. [11] EXCELITAS Co. High-speed low-light analog APD receiver modules LLAM Series. www.excelitas.com.[EB/OL]. (2017-12-11).http://www.excelitas.com/Downloads/DTS_LLAM.pdf. [12] ANALOG DEVICES Inc. AD8367 www.analogy.com.[EB/OL]. (2018-1-16).http://www.analog.com/media/en/technical-documentation/data-sheets/AD8367.pdf. -
点击查看大图
图(9)
计量
- 文章访问数: 7150
- HTML全文浏览量: 4958
- PDF下载量: 191
- 被引次数: 0
