Construction of experimental 3-D point spread function of digital confocal microscopy
-
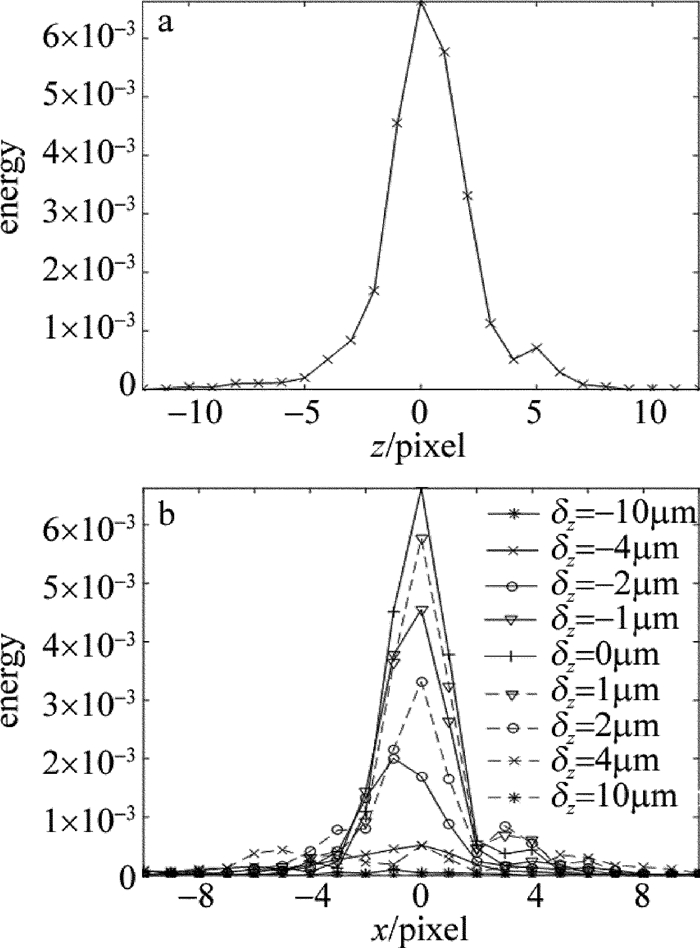
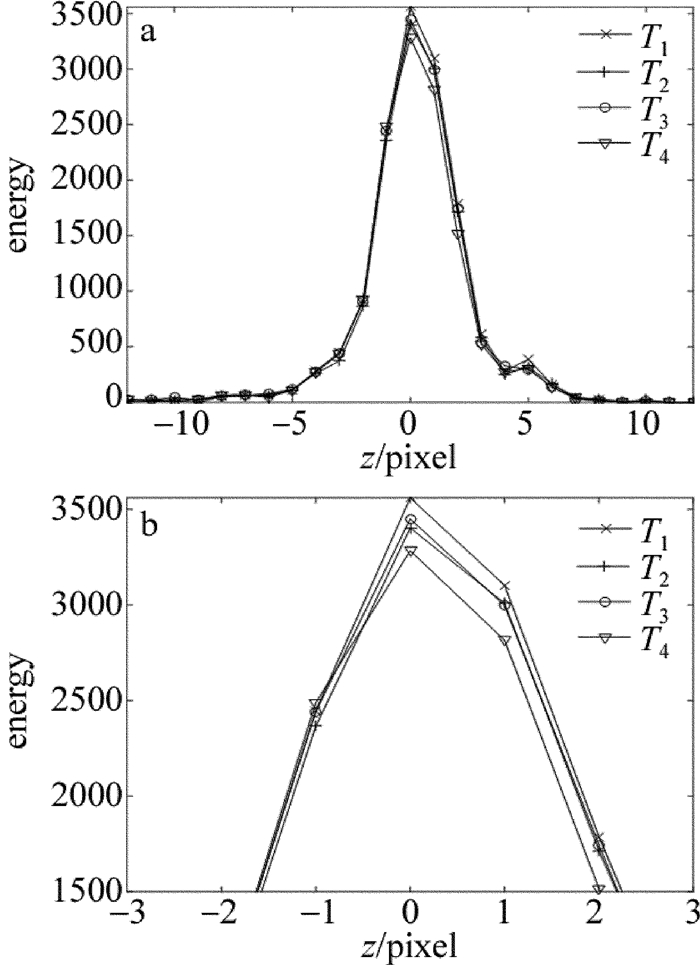
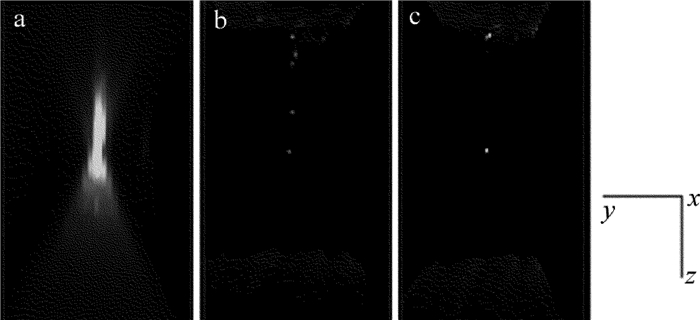
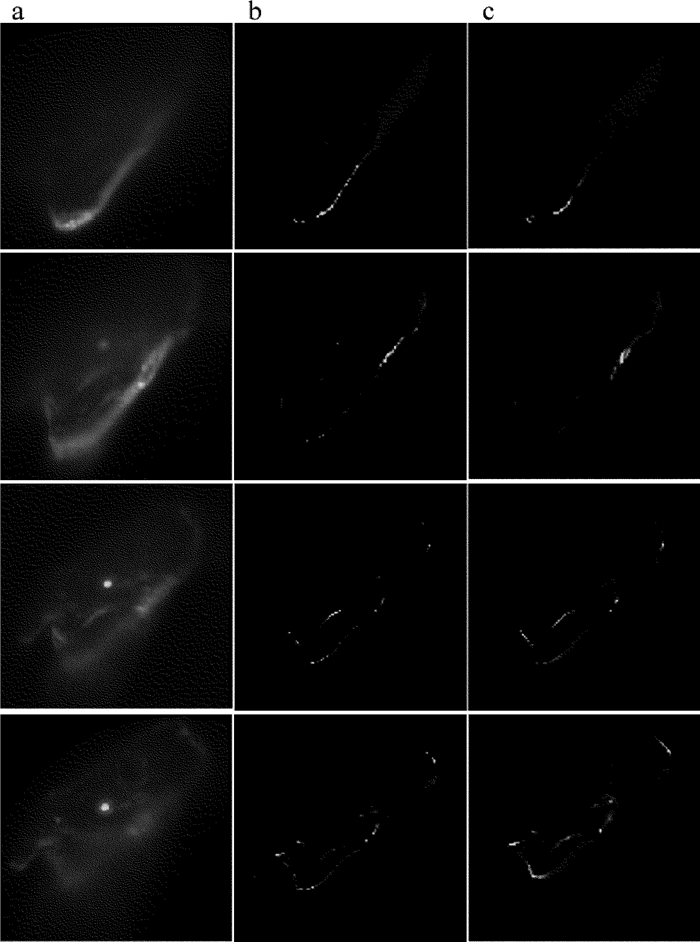
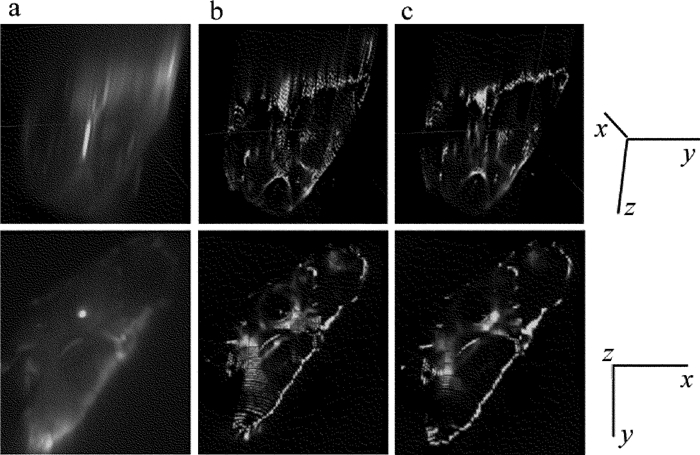
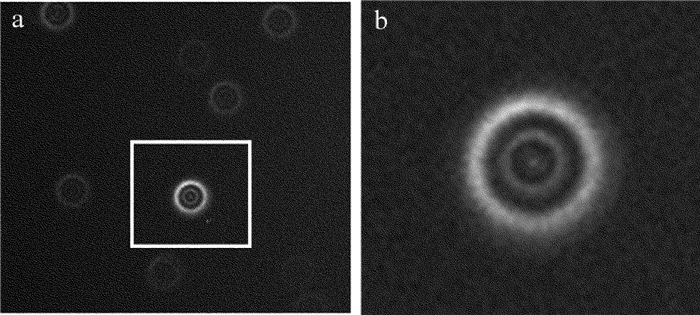
摘要: 为了获取作者所在实验室数字共焦显微镜光学系统实验3维点扩散函数，采用荧光微珠模拟点光源，利用该显微镜对荧光微珠不同散焦量的切片图像进行采集，采用多图像平均法对切片图像进行降噪处理，以此构建显微镜光学系统的实验3维点扩散函数。以该实验点扩散函数进行3维显微图像复原，并与理论点扩散函数的复原效果进行了比较。结果表明，两种点扩散函数对图像复原时均获得良好的复原效果，但是以正确实验方法获取的实验3维点扩散函数，更符合该光学系统的光学传递特性，复原效果更准确。所构建的实验3维点扩散函数，为下一步的生物显微图像复原处理提供了一种较好的选择，为数字共焦显微镜实验3维点扩散函数的构建提供了一种有效的方法。Abstract: In order to obtain experimental 3-D point spread function of a digital confocal microscope optical system, a fluorescence microsphere was used to simulate the point light source, a digital confocal microscope optical system was used to collect the slice images of the fluorescent microsphere with different defocuses, and the multi-image averaging method was used to denoise the slice images. Experimental 3-D point spread function of the microscope optical system was constructed. 3-D microscopic image restoration was carried out by experimental point spread function and was compared with that of theoretical point spread function. The results show that both the point spread functions have good restoration effect for image restoration, but experimental 3-D point spread function obtained by correct experimental method is more consistent with optical transmission characteristics of an optical system and has more accurate recovery effect. Experimental 3-D point spread function constructed in the study provides a better choice for the next step of biological microscopic image restoration. It provides an effective method for the construction of 3-D point spread function of digital confocal microscopes.
-
-
![]()
Figure 3. Energy distribution of experimental 3-D-PSF a—along z axis b—along radial direction
![]()
Figure 4. Energy distribution of PSF made by 4 experiments a—energy distribution of center point b—partial enlargement
![]()
Figure 7. Energy distribution of theoretical 3-D-PSF a—along z axis b—along radial direction
-
[1] SHU X Y, LI J T. Information optics[M].Beijing:Science Press, 1999:63-77(in Chinese).
[2] CHEN H, JING W Q, WANG X, et al. Investigation about 3-D microscopically image restoration and PSF[J]. Optical Technique, 2006, 32(3):434-439(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-GXJS200603033.htm
[3] LI R, TAO Q Ch, HE X H, et al. Nearest-neighbors subtraction algorithm based on Gaussian point spread function estimation[J]. Opto-Electronic Engineering, 2007, 34(6):1-6(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc200706020
[4] YANG F J. Research of space size selection method of three-dimensional point spread function[D].Nanning: Guangxi University, 2014: 27-46(in Chinese).
[5] HOPKINS H H. The frequency response of a defocused optical system[J]. Proceedings of the Royal Society of London, 1955, A231(1184):91-103. http://www.jstor.org/stable/99629
[6] STOCKSETH P A. Properties of defocused optical system[J]. Journal of the Optical Society of America, 1969, A59(10):1314-1321. DOI: 10.1364-JOSA.59.001314/
[7] AGARD D A. Optical sectioning microscopy:cellular architecture in three dimensions[J]. Annual Review of Biophysics and Bioengineering, 1984, 13(1):191-219. DOI: 10.1146/annurev.bb.13.060184.001203
[8] PREZA C, CONCHELLO J A. Theoretical development and experimental evaluation of imaging models for differential-interference-contrast microscopy[J]. Journal of the Optical Society of America, 1999, A16(9):1593-1601. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=25f1a54068a996f85151c0d7aee646c0
[9] CASTLEMAN K R. Digital image processing[M]. Beijing:Publishing House of Electronics Industry, 2011:469-473(in Chinese).
[10] CHEN H. Research on digital confocal microscopic image recovery and its system implementation[D].Beijing: Beijing Institute of Technology, 2005: 20-45(in Chinese).
[11] LU W M, YANG X B, WEN G, et al. An optimized model of point spread function of microscopy based on fluorescence beads[J]. Laser Technology, 2016, 40(5):638-642(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201605005
[12] WANG F P. The measurement of the point spread function in optical system with CCD[J]. Journal of Gannan Teachers College, 2005, 26(6):17-18(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GNSY200506005.htm
[13] KENNETH R C. Digital image processing[M].Beijing:Publishing House of Electronics Industry, 2002:350-380.
[14] SIBARITA J B. Deconvolution microscopy[J]. ADV Biochem Engin/Biotechnol, 2005, 95:201-243. DOI: 10.1007/b14097
[15] RAYLEIGH L. On the theory of optical image, with special reference to the microscope[J]. Journal of the Royal Microscopical Society, 2011, 42(255):167-195. DOI: 10.1111/j.1365-2818.1903.tb04830.x/full
[16] AYERS G R, DAINTY J C. Iterative blind deconvolution method and its applications[J]. Optics Letters, 1988, 13(7):547-549. DOI: 10.1364/OL.13.000547
下载:
计量
- 文章访问数: 6
- HTML全文浏览量: 1
- PDF下载量: 5