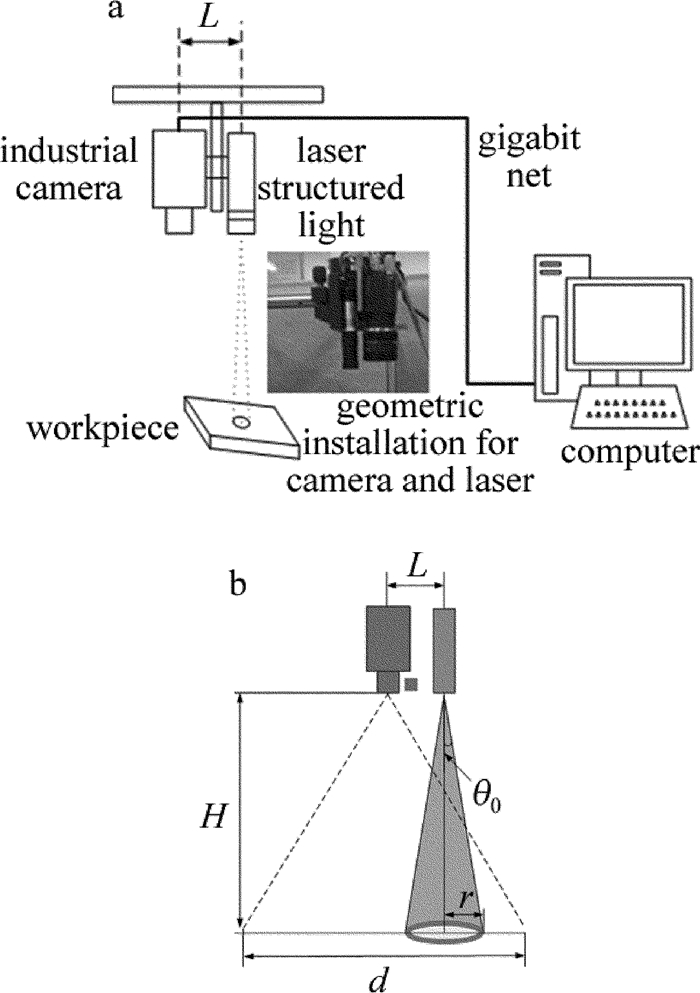
Six-DOF attitude transform visual experiment platform and its application
-
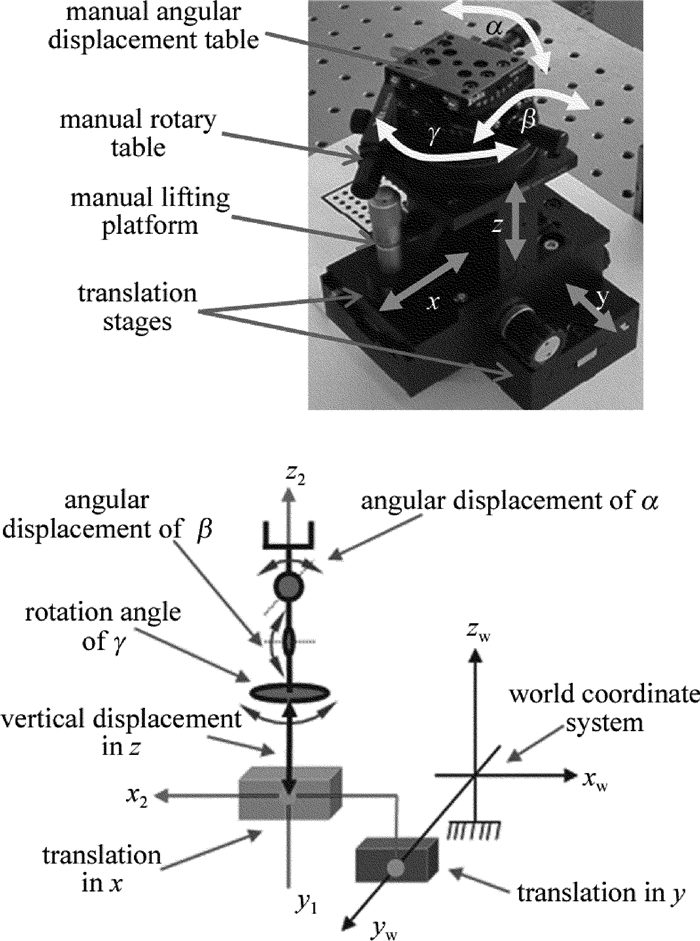
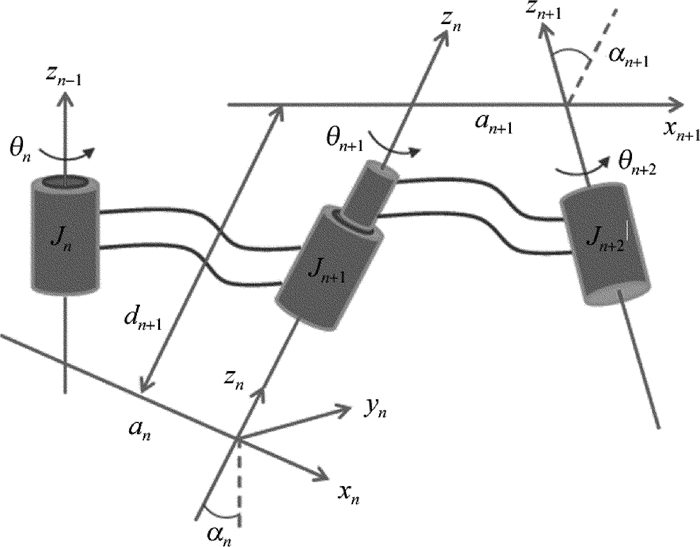
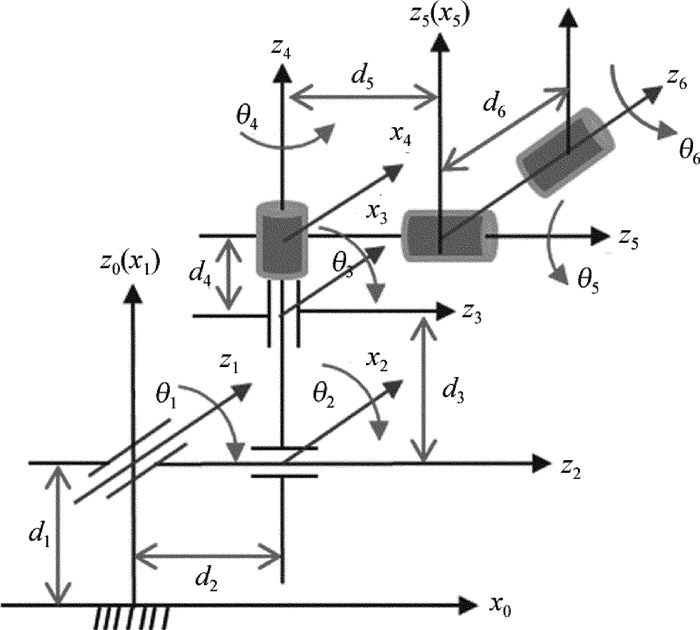
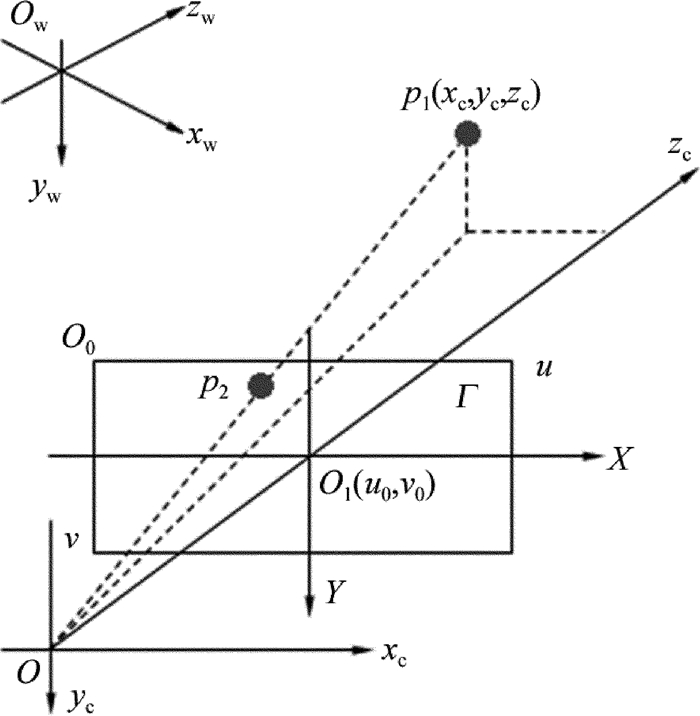
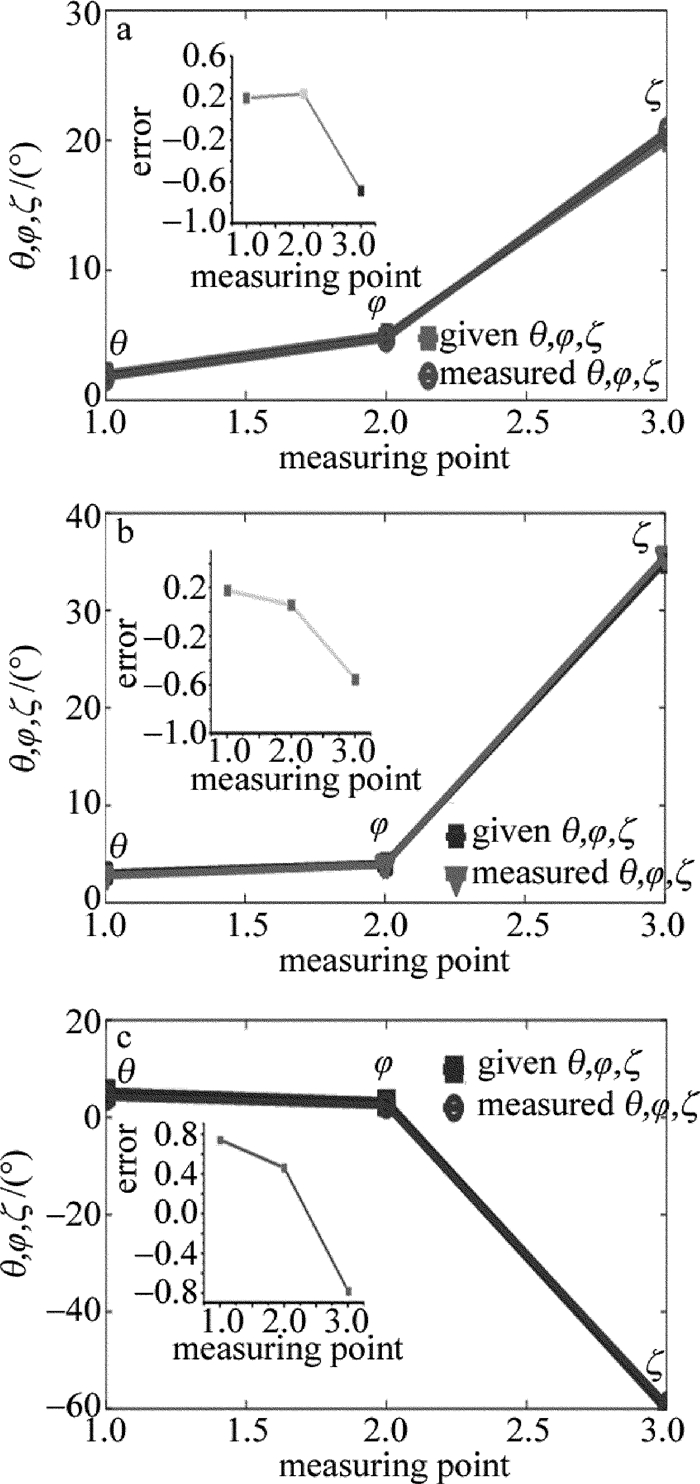
摘要: 为了适应生产线上不同摆放姿态下工件的视觉识别,实现基于视觉的机器人工件定位及抓取,构建了六自由度工件姿态变换模拟实验平台运动学模型及视觉系统模型,通过坐标变换实现工件姿态参量的测量。建立了六自由度姿态变换实验平台坐标系,通过3个滑动副、3个转动副,构建了基于Denavit-Hartenberg(D-H)方法的六自由度姿态变换实验平台运动学模型,并得到了D-H参量表、各个关节的变换矩阵及实验平台基座到末端的总变换矩阵。基于小孔成像原理,构建了姿态变换实验平台视觉系统的内、外参量模型,获得了工件表面点与图像点间的内参量关系矩阵及工件坐标系与相机坐标间的外关系矩阵。由激光环形光条图像,得到工件表面在摄像机坐标系中的法向量,并通过坐标系间的变换得到工件表面在世界坐标系中的法向量,进而推算出工件的姿态参量。结果表明,姿态参量的横滚角θ平均误差为0.373°,俯仰角φ平均误差为0.253°,偏转角ξ平均误差为0.673°。被测工件的姿态测量值与真实值基本吻合,满足不同姿态下的工件视觉测量要求。
-
关键词:
- 测量与计量 /
- 姿态变换 /
- 视觉测量 /
- 六自由度 /
- Denavit-Hartenberg模型
Abstract: In order to adapt the visual recognition of workpiece with different postures in production line and realize the localization and grasping of workpiece based on vision robot, the kinematics model and the visual system model of six degree of freedom(6-DOF) workpiece attitude transformation simulation experiment platform were constructed. The measurement of attitude parameters of workpiece was realized by coordinate transformation. 6-DOF attitude transformation experimental platform coordinate system was set up. Kinematics model of six degree of freedom attitude transformation experiment platform based on Denavit-Hartenberg (D-H) method was constructed through 3 sliding pairs and 3 rotational pairs. D-H parameter table, transformation matrix of each joint and total transformation matrix of experimental platform from the base to the end were obtained. Based on the principle of small hole imaging, the internal and external parameter model of attitude transformation experimental platform was constructed. The internal parameter relation matrix between workpiece surface point and image point and the external relation matrix between workpiece coordinate system and camera coordinate system were obtained. The normal vector of workpiece surface in camera coordinate system was obtained from the image of laser ring light strip. And then, the normal vector of workpiece surface in the world coordinate system was obtained through the transformation of coordinate system. Finally, attitude parameters of workpiece were calculated. The results show that average error of roll angle is 0.373°, average error of pitch angle is 0.253° and average error of deflection angle is 0.673°. The measured value of workpiece is basically consistent with the true value, which meets the requirements of workpiece vision measurement under different postures. -
-
Table 1 D-H parameter table of attitude simulation experiment platform
connecting rod
iangle
θi/(°)spacing
diconnecting rod
length ai-1/mmtwist angle
αi-1/(°)1 -90 0 0 -90 2 -90 d2 0 -90 3 0 d3 0 -90 4 0 d4 0 0 5 90 d5 0 90 6 0 d6 0 90 Table 2 Measurement results for workpiece attitude
No. given value (θ, φ, ξ)/(°) normal vector measured value (θ, φ, ξ)/(°) 1 (2.0, 5.0, 20.0) (0.0831, 0.0314, 0.9965) (1.80, 4.76, 20.69) 3 (3.0, 4.0, 35.0) (0.0687, 0.0491, 0.9964) (2.82, 3.94, 35.55) 5 (5.0, 3.0, -60.0) (-0.0442, 0.0742, 0.9960) (4.26, 2.54, -59.22) -
[1] HUANG Zh, LI Y W, GAO F. The expression of the orientation of a spatial moving unit by euler angle[J] Journal of Yanshan University, 2002, 26(3):189-192(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DBZX200203000.htm
[2] JIANG Sh P, GUO Zh, SUN H D. Modeling and Simulation for caudal fin motion of dolphin robot[J]. Journal of Yanshan University, 2008, 32(4):311-315(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-DBZX200804008.htm
[3] CHEN Zh K, XU A, WANG F B, et al. Pose measurement of target based on monocular vision and circle structured light[J]. Journal of Applied Optics, 2016, 37(5):680-685(in Chinese). http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-YYGX201605008.htm
[4] YU Q F, SUN X Y, CHEN G J. A new method of measure the pitching and yaw of the axes symmetry object through the optical image[J]. Journal of National University of Defense Technology, 2000, 22(2):15-19(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GFKJ200002003.htm
[5] LI H, YANG D H, ZHAI Ch. Research on the pose measurement of a 6-DOF platform using a single camera[J]. Optical Technique, 2010, 36(3):344-349(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-GXJS201003004.htm
[6] FISCHLER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6):381-395. DOI: 10.1145/358669.358692
[7] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP:An accurate O(n) solution to the PnP problem[J]. International Journal of Computer Vision, 2009, 81(2):155-166. DOI: 10.1007/s11263-008-0152-6
[8] STEWÉNIUS H, ENGELS C, NISTÉR D. Recent developments on direct relative orientation[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2006, 60(4):284-294. DOI: 10.1016-j.isprsjprs.2006.03.005/
[9] LI G L, J Ch Y, GU B X, et al. Kinematics analysis and experiment of apple harvesting robot manipulator with multiple end-effectors[J]. Transactions of the Chinese Society of Agricultural Machinery, 2016, 47(12):14-21(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201612003
[10] QI J D, ZHANG D H, LI Sh, et al. Modeling and compensation of absolute positioning error of industrial robots[J]. Journal of South China University of Technology(Natural Science Edition), 2016, 44(11):113-118(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-HNLG201611017.htm
[11] ZHANG X, ZHENG Z L, QI Y. Parameter identification and calibration of D-H model for 6-DOF serial robots[J]. Robot, 2016, 38(3):360-370(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jqr201603013
[12] MO Y. D-H modeling and simulation analysis based on six degree of freedom industrial robot[J]. Machine Tool & Hydraulics, 2017, 45(11):64-68(in Chinese). http://www.en.cnki.com.cn/Article_en/CJFDTotal-JCYY201711015.htm
[13] YOUNG K Y, CHEN J J. Implementation of a variable D-H parameter model for robot calibration using an FCMAC learning algorithm[J]. Journal of Intelligent & Robotic Systems, 1999, 24(4):313-346. DOI: 10.1023/A%3A1008094014724
[14] CHALAK Q M R, SIAMAK P, ARASH R, et al. Kinematic analysis and workspace determination of hexarot-a novel 6-DOF parallel manipulator with a rotation-symmetric arm system[J]. Robotica, 2015, 33(8):1686-1703. DOI: 10.1017/S0263574714000988
[15] CAI C, SOMANI N, KNOLL A. Orthogonal image features for visual servoing of a 6-DOF manipulator with uncalibrated stereo cameras[J]. IEEE Transactions on Robotics, 2016, 32(2):452-461. DOI: 10.1109/TRO.2016.2535443
[16] HSIEH H L, PAN S W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements[J]. Optics Express, 2015, 23(3):2451-2465. DOI: 10.1364/OE.23.002451
[17] XU D, TAN M, LI Y.Visual measurement and control for robots[M].Beijing:National Defence Industrial Press, 2008:39-118(in Chinese).
[18] WANG F B, LIU J, LI Y Y, et al. The camera parameter calibration of excavator robot based on OpenCV[J]. Journal of Liaoning Technical University (Natural Science Edition), 2010, 29(6):1117-1120(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-FXKY201006029.htm
[19] LI B, YUAN F B, LI F N, et al. Feature analysis of coaxial monitoring of welding pool and keyhole during laser deep penetration welding[J]. Laser Technology, 2017, 41(2):255-259(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201702022.htm
[20] YAN B, WANG B, LI Y. Optimal ellipse fitting method based on least-square principle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(3):295-298(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-BJHK200803011.htm




 下载:
下载: