网站地图
下载:
-
电磁超材料是由用来模拟电/磁偶极子的亚波长结构单元排列而成的等效介质。它的介电常数和磁导率[1-3]可以通过设计结构单元及其排列方式来调控。利用超材料，人们不但可以实现对电磁波传播的有效操控而且可以模拟一些有趣的物理效应，比如电磁诱导透明效应[4]、克尔效应[5-6]、负折射效应[7-8]等，同时还可以用来设计一些特殊的微波器件，如超棱镜[9-10]、隐身斗篷[11-12]等。因此，电磁超材料能够用于设计民用或军用上的微波器件[13]。
在2008年，LANDY等人首次提出了电磁超材料完美吸波器的设计概念[14]，随后，TAO[15]等人基于电谐振设计了一种工作在THz波段的超材料吸波器。由此电磁吸波器便成为了研究热点，在理论和实验研究上都取得了许多令人瞩目的成果。目前有关吸波器的研究工作主要集中在多频带吸波[16-18]、宽带吸波[19-21]、极化不敏感[22]、大角度入射[23-24]、超薄结构设计[25]等方面。然而，常规吸波器最大的缺陷是很难得到可调谐的吸收频谱。
等离子体超材料是超材料的一种，它一般由等离子体介质周期结构构成，并可以通过调节等离子体的频率(密度)或激励不同谐振区域来改变其物理特性。用等离子体材料设计吸波器可以得到可调谐的吸收频谱。关于等离子体超材料吸波器的研究尚处于起步阶段，因此，研究等离子体超材料吸波器的设计方法和理论具有重要的意义。
作者设计了一种能工作在微波频段的基于等离子体超材料的吸波器，通过改变等离子体的激励区域来实现对吸收频谱的动态调控。在理论上，用全波仿真法计算得到的吸收频率研究了该吸收器的电磁特性，并探讨了该吸波器吸收效应的物理机理。
-
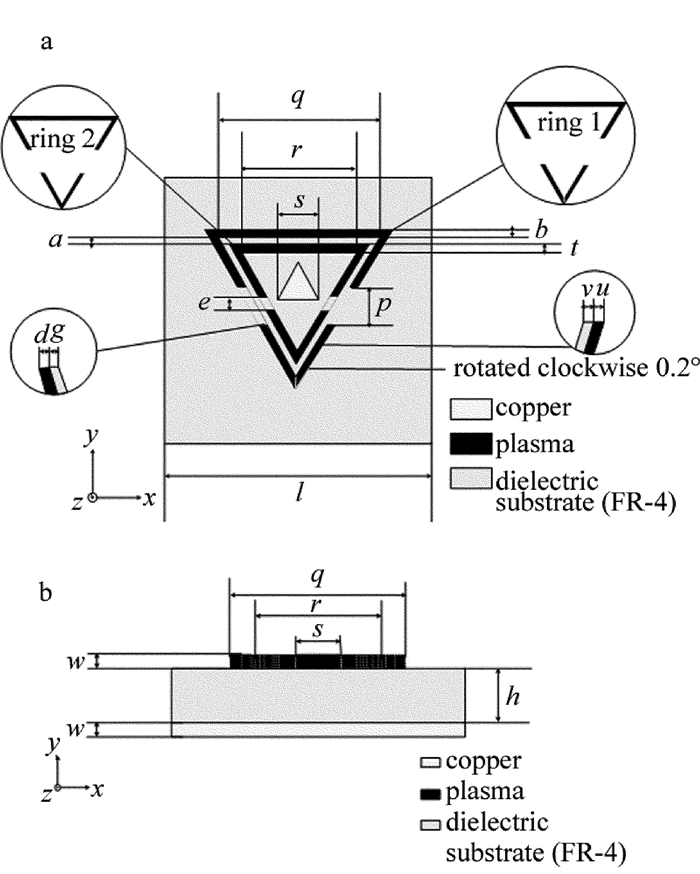
图 1是作者设计的等离子体材料吸波器的单元结构示意图。图 1a是正视图，图 1b是侧视图。由图 1可知，该结构单元的底层为金属铜板(电导率为σ=5.8×107S/m)，中间层为介质基板，上层由被截断的等离子体环形结构和三角形金属铜片构成。介质基板为FR-4(相对介电常数εr=4.3，损耗角正切tanδ=0.025)，介质基板厚度h=2.9mm，介质基板的边长l=72mm，上层贴片和底层金属铜板的厚度w=0.04mm，外层等离子体谐振环(ring 1)和内层等离子体谐振环(ring 2)的间距a=1mm，外层环的边长q=50.821mm，表示为3l/5+22x/5，其中$x = \sqrt {3a} $，内层环的边长r=43.2mm，表示为3l/5，中间三角贴片的边长s=18.6mm，表示为$\frac{{3l}}{{10}} - \sqrt {3x} $，外层环的上下谐振单元间距p=14.314mm，表示为24x/5+2c，其中c=0.2mm，内层环的上下谐振单元间距e=2mm，外层环上面谐振单元的宽度b=1.8mm，内层环上下谐振单元的宽度t=1.2mm，外层环下面的“V”型结构中左边谐振单元的宽度d=1.2mm，与内层环下面的“V”型谐振单元的间距g=1mm，外层环下面的“V”型结构中右边谐振单元的宽度u=1.2mm，与内层环下面的“V”型谐振单元的间距v=0.9mm，上层等离子体的介电常数用Drude模型来描述:
Figure 1. Structure schematic of the unit cell for the proposed absorber
$ {\varepsilon _{\rm{p}}}\left( \omega \right) = 1 - \frac{{\omega _{\rm{p}}^2}}{{{\omega ^2} + {\rm{j}}\omega {\omega _{\rm{c}}}}} $
(1) 式中, ω表示角频率，等离子频率ωp=2.9×1015rad/s, 碰撞频率ωc=1.65×10141/s。电磁波波矢方向为沿着-z方向垂直入射，本文中提及的TE波为电场平行于y轴，磁场平行x轴。吸波器的吸收率A(ω)可以表示为:
$ A\left( \omega \right) = 1 - R\left( \omega \right) - T\left( \omega \right) $
(2) 式中, R(ω)为反射率，T(ω)为透射率。由于本文中设计的吸波器底层为金属铜板，所以透射率T(ω)=0，那么吸收率表示为:
$ A\left( \omega \right) = 1 - R\left( \omega \right) $
(3) 由(3)式可知，如果R(ω)越小，那么A(ω)的值就越大。
-
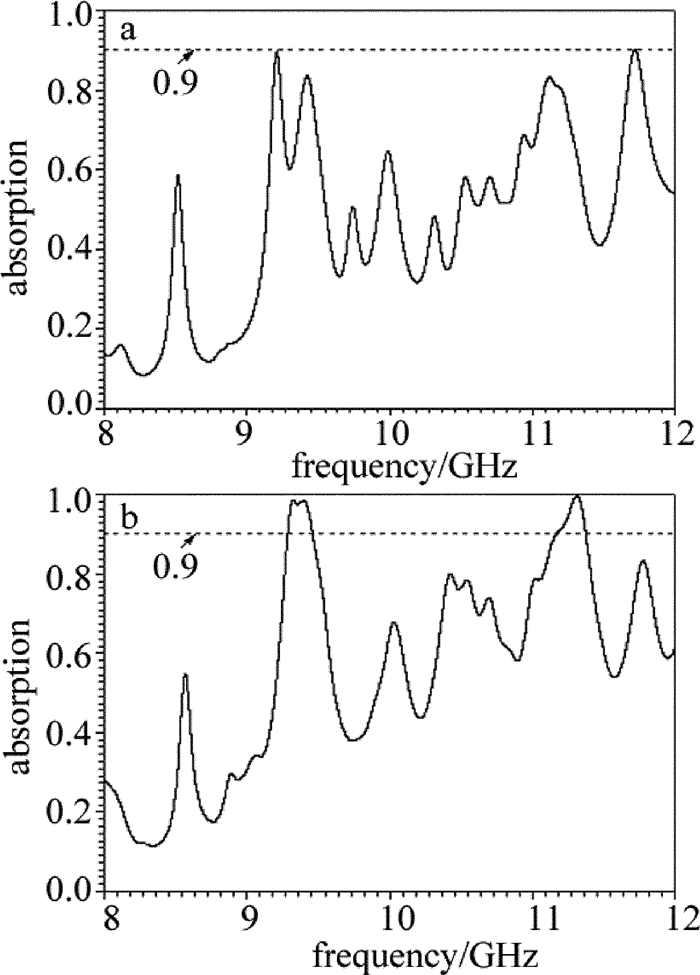
图 2中给出了激励不同等离子体谐振单元时的吸收频谱。如图 2a所示(ring 1中的等离子体谐振结构被激励，而ring 2中的等离子体谐振结构未被激励)，吸收频谱中存在着两个吸收率较高的频点，它们的值分别为89.69%和90.04%，位于9.2GHz和11.71GHz。显然，此时该吸波器的吸波效果较差。如果ring 1和ring 2中等离子体谐振结构同时被激励，其吸收频谱如图 2b所示。由图 2b所示，在8GHz~12GHz的频率范围内存在着两个吸收率大于90%的吸收频域，它们分别为9.16GHz~9.36GHz和11.16GHz~11.38GHz。在9.19GHz, 9.31GHz和11.31GHz处的吸收率分别达到99.03%, 95.92%和99.21%。比较图 2a和图 2b中的结果可知，ring 1和ring 2中等离子体谐振结构同时被激励时，该吸波器的吸波特性得到了明显地改善。显然，人为地改变上层等离子体谐振结构的激励形态，不仅可以改善该吸波器的吸收特性，还能实现对吸收频域的可调谐。换句话说，可以以最为简单的单极化多频吸波器为起点，实现极化不敏感的宽频吸波器的设计。从这个角度出发，采用最简单的电谐振吸波器的设计思路(单极化)，通过等离子体超材料的可调谐性实现了由频谱中的单频吸收与窄带吸收间的相互切换(极化敏感)，也为下一步设计极化不敏感的宽频吸波器奠定了基础。
Figure 2. Absorption spectra of the proposed absorber
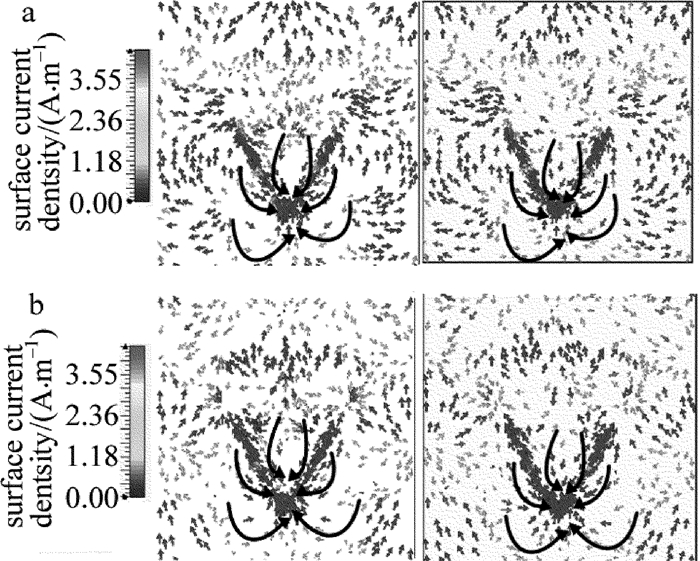
为了研究该吸波器工作的物理本质，进一步地理解电磁波损耗的机理，对该吸波器在f1=9.19GHz和f2=9.31GHz两个频点处的表面电流进行了计算。图 3是该吸波器在这个两点频点上的上表面和背面的电流分布图。由图 3可知，当垂直入射的TE波的频率分别为f1=9.19GHz和f2=9.31GHz时，在该吸波器的上下表面都会形成表面电流。对于上表面而言，其表面电流主要集中在上表面的两个“V”形等离子体谐振结构的底部，其电流方向如图中黑色箭头所示。由图 3还可知，在这两个吸收频点该吸波器的背面同样也会产生表面电流，其表面电流也主要集中在正对上表面“V”形谐振结构底部处，其表面电流的方向与上表面的相同。此时，该吸波器的上下表面可以看成一个电偶极子，将在上下层间形成电谐振。这种电谐振将会和外部入射的电磁波进行耦合，使得入射电磁波的能量在介质基板中被损耗，从而实现了该吸波器在这两个频点吸波。因此，该吸波器主要是电谐振的形式来实现对入射电磁波的吸收。
Figure 3. Surface current (left) and backplane surface current (right) at different resonant frequencies
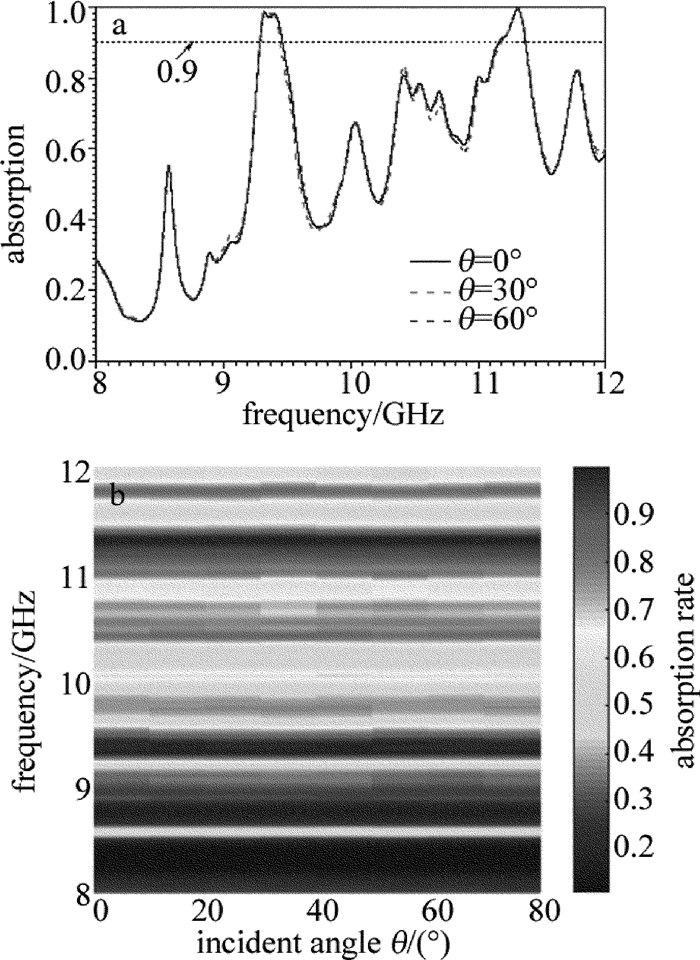
图 4中给出了入射角θ(入射电磁波矢与y-O-z面的夹角)与吸收频谱的关系图。由图 4a可知，当入射角θ分别为0°, 30°和60°时，该吸波器的吸收频谱几乎没有发生变化，在9.16GHz~9.36GHz和11.16GHz~11.38GHz这两个频域范围内其吸收率都可以达到90%以上，其吸收率峰值分别位于9.32GHz, 9.39GHz和11.3GHz，它们的值分别为98.5%, 98.8%和99.6%。显然，该吸波器的角度稳定性较好，随着入射角θ的增大，该吸波器的最大吸收率会有所增加。为了进一步说明这个问题，图 4b中给出了入射角θ与吸收率的关系图。由图 4b可知，当入射角θ由0°连续变化到80°时，该吸波器的吸波特性几乎保存不变。随着入射角θ的增大，吸收频域上下边缘会略微地向高频方向移动。当θ=80°时，改变吸波器的工作频域(吸收率大于90%)变为9.27GHz~9.45GHz和11.16GHz~11.38GHz。因此，由图 4中的结果可知，该吸波器具有较好的角度稳定性。
Figure 4. a—relationship between absorption spectrum and frequency at different incident angles b—relationship between frequency and incident angle
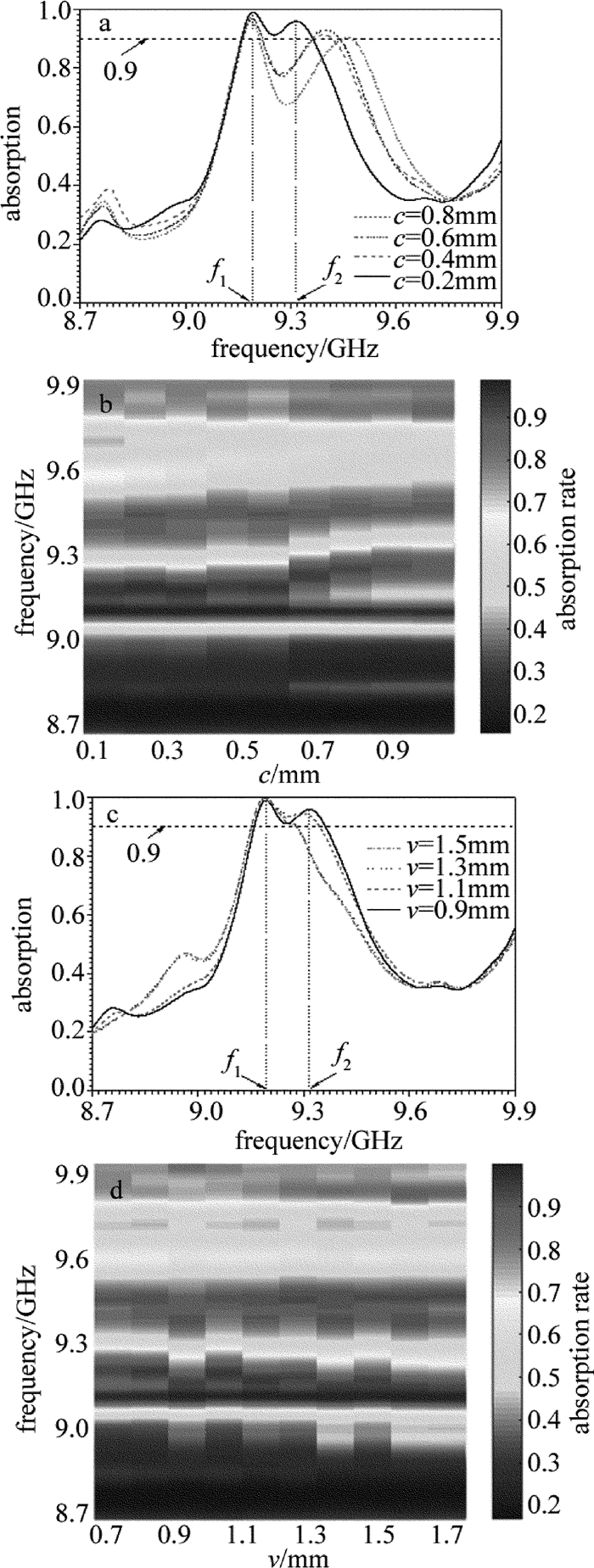
为了进一步研究该吸波器的特性，在图 5中给出了结构参量c和v对吸收频谱的影响。图 5a给出了其它参量不变的情下，结构参量c为0.2mm，0.4mm，0.6mm和0.8mm时的吸收频谱。由图 5a可知，c=0.2mm时，在频率范围8.7GHz~9.9GHz内该吸波器工作频域为9.16GHz~9.36GHz，且有两个吸收峰值分别为99%和94.9%位于f1=9.19GHz和f2=9.31GHz。随着c的增大，该吸波器的工作频域将逐渐减小。当c为0.4mm，0.6mm和0.8mm时，该吸波器的工作频域分别为9.16GHz~9.23GHz，9.16GHz~9.21GHz和9.16GHz~9.20GHz。但f1=9.19GHz处的第一吸收峰值将几乎保持不变，而第二吸收峰将随着c的增大而减小，并向高频方向移动。为了进一步说明这个问题，图 5b中给出了吸收频谱与结构参量c的关系图。由图 5b可知，f1=9.19GHz处的第一吸收峰值几乎不会随着c的增大而变化，而该吸波器工作频域将会随着c的增大先增大后减小，最后再保持不变。c=0.2mm时，该吸波器的工作带宽最宽，即0.20GHz。当c≥0.6mm时，该吸波器的工作带宽最窄，且几乎不会随着c的增大而发生变化，即0.04GHz，位于9.16GHz~9.20GHz。显然，改变参量c的值不仅能够对该吸波器的工作频域进行调谐，还能对第二吸收峰的大小和位置进行调谐。同样，图 5c中给出了其它参量不变的情况下, 结构参量v为0.9mm, 1.1mm, 1.3mm和1.5mm时的吸收频谱。由图 5c可知，v=0.9mm时，该吸波器工作频域为9.16GHz~9.36GHz，且两个吸收峰值分别位于f1=9.19GHz和f2=9.31GHz。随着参量v的增大，该吸波器的工作带宽也将逐渐地减少。但第一吸收峰的频率将保持f1=9.19GHz不变，而第二吸收峰的频率f2将随着参量v的增大而向低频方向移动。当v为1.1mm, 1.3mm和1.5mm时，该吸波器的工作频域分别为9.16GHz~9.34GHz, 9.16GHz~9.279GHz和9.16GHz~9.277GHz。图 5d中给出了吸收频谱与结构参量v的关系图。由图 5d可知，该吸波器工作频域将会随着v的增大先增大后减小。v=0.9mm时，该吸波器的工作带宽最大且等于0.20GHz。v=1.7mm时，该吸波器的工作带宽最小且等于0.13GHz，位于9.14GHz~9.27GHz。显然，改变参量v的值对该吸波器的工作带宽有明显的调谐作用。综上所述，只要人为地改变等离子体谐振结构的激励区域(如改变结构参量c和v的大小)就可以得到可调谐的吸收频谱，通过相应的参量优化就能拓展该吸波器的工作频域。
Figure 5. a—relationship between absorption spectrum and frequency with di-fferent c b—relationship between frequency and c c—relationship between absorption spectrum and frequency with different v d—relationship between frequency and v
-
设计了一款基于等离子体超材料的吸波器，能够实现在TE波下得到可调谐的吸收频谱。采用了全波仿真方法对该吸波器的吸收频谱和表面电流图进行了计算，并探讨了结构参量c, v和入射角度θ对吸收率的影响。研究结果表明：通过激励不同的等离子体谐振结构不但可以改善该吸波器的吸收特性，而且还能获得可调谐的吸收频谱。该吸波器的工作频谱位于9.16GHz~9.36GHz和11.16GHz~11.38GHz，其吸波机理主要是通过电谐振的方式使得入射电磁波的能量在介质基板中得以损耗。当入射角θ的值发生改变时，该吸波器的工作频域几乎不发生变化，即该吸波器具有较好的角度稳定性。改变参量c和v的大小都能够实现对吸收频谱的调谐。增加参量c的值，该吸波器的工作频域将先增大后减少最后趋于一个定值(9.16GHz~9.20GHz)，而增加参量v的值，该吸波器的工作频域将先增大后减少，其最小值为9.14GHz~9.27GHz(v=1.7mm)。吸收频谱中的第一峰的位置(f1=9.19GHz)将不会随着c和v的变化而变化，而第二吸收峰的位置f2将随着c的增大而向高频方向移动，而随着v的增大而向低频方向移动。显然，只要人为地调控激励等离子体谐振单元的区域，不但能够都到可调谐的吸收频谱, 还能拓展吸波器的工作带宽。该研究也为设计新型波器吸提供了思路。
一种基于等离子体超材料的吸波器设计
Design of an absorber based on plasma metameterial
-
摘要: 为了在TE波下获得可调谐的吸收频谱，设计了一款基于等离子体超材料的吸波器。采用全波仿真方法对该吸波器的吸收率和表面电流图进行了计算，并探讨了结构参量c，v和入射角度θ对吸收率的影响。结果表明，通过激励不同的等离子体谐振区域不但可以改善其吸收特性，而且还能获得可调谐的吸收频谱；改变结构参量c和v可以在实现拓展吸收带宽的同时，使得吸收频域也发生移动；改变入射角度θ的大小对吸收率的影响不大。该吸波器具有很好的角度稳定性。Abstract: In order to obtain tunable absorption spectra under TE wave, an absorber was designed based on plasma metamaterial. The absorption spectra and the distribution of surface current of the absorber were computed by means of full-wave simulation. The effect of structural parameters c, v and incident angle θ on absorption spectra was also discussed. The simulated results demonstrate that not only the tunable absorption spectra can be obtained in the proposed absorber but also the properties of absorption can be improved by exciting the different plasma resonance structures. Changing the structural parameters of c and v, the absorption bandwidth can be widened and its location can be tuned at same time. The incident angle θ has little effect on the absorption spectra. The proposed absorber has good angular stability.
-
Key words:
- physical optics /
- plasma metameterial /
- absorber /
- tunable properties
-
Figure 1. Structure schematic of the unit cell for the proposed absorber
a—the front view b—the side view
Figure 2. Absorption spectra of the proposed absorber
a—with ring 1 —with ring 1 and ring 2
Figure 3. Surface current (left) and backplane surface current (right) at different resonant frequencies
a—9.19GHz b—9.31GHz
Figure 4. a—relationship between absorption spectrum and frequency at different incident angles b—relationship between frequency and incident angle
-
[1] PENDRY J B, HOLDEN A J, ROBBINS D J, et al. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Transactions on Microwave Theroy and Techniques, 1999, 47(11):2075-2084. doi: 10.1109/22.798002 [2] SMITH D R, PADILLA W J, VIER D C, et al. Composite medium with simulataneously negative permeability and permittivity[J]. Physical Review Letters, 2000, 84(18):4184-4187. doi: 10.1103/PhysRevLett.84.4184 [3] SMITH D R, SCHURING D. Electromagnetic wave propagation in media with indefinite permittivity and permeability tensors[J]. Physical Review Letters, 2003, 90(7):077405. doi: 10.1103/PhysRevLett.90.077405 [4] JAEYOUN K, RICHARD S, WALTER R B. Multi-peak electromagnetically induced transparency(EIT)-like transmission from bull's-eye-shaped metamateria[J]. Optics Express, 2010, 18(17):17997-18002. doi: 10.1364/OE.18.017997 [5] ALEXANDER A Z, VLADISLAV V K. Giant resonant mageto-optic Kerr effect in nanostructured ferromagnetic metamaterial[J]. Journal of Applie Physics, 2007, 102(12):123514. doi: 10.1063/1.2822192 [6] HU Y H, WEN S C, ZHUO H, et al. Focusing properties of Gaussian beams by a slab of Kerr-type lefthanded metamaterial[J]. Optics Express, 2008, 16(7):4774-4784. doi: 10.1364/OE.16.004774 [7] VESELAGO V G. The electrodynamics of substances with simulaneously negative values of ε and μ[J]. Soviet Physics Uspekhi, 1968, 10(4):509-514. doi: 10.1070/PU1968v010n04ABEH003699 [8] SHELBY R A, SMITH D R, SCHULTZ S. Experimental verification of a negative index of refraction[J]. Science, 2001, 292(5514):77-79. doi: 10.1126/science.1058847 [9] PENDRY J B. Negative refraction makes a perfect lens[J]. Physical Review Letters, 2000, 85(18):3966-3969. doi: 10.1103/PhysRevLett.85.3966 [10] FANG N, LEE H, SUN C, et al. Sub-diffraction-limited optical imaging with a sliver superlens[J]. Science, 2005, 308(5721):534-537. doi: 10.1126/science.1108759 [11] SCHURIG D, MOCK J J, JUSTICE B J, et al. Metamaterial electromagnetic cloak at microwave frequencies[J]. Science, 2006, 314(5801):977-980. doi: 10.1126/science.1133628 [12] LIU Y W, WANG X H, DONG Z D, et al. Tunable electromagnetic cloaking by external field[J]. Transactions of Nanjing University of Aeronzutics & Astronautics, 2014, 31(3):241-248. [13] YIN Q T, YAO G, SHI S J, et al. Study on transparency structure induced by tunable teraherz plasmon. Laser Technology, 2017, 41(6):826-830(in Chinese). [14] LANDY N I, SAIUYIGBE S, MOCK J J, et al. Perfect metamaterial absorber[J]. Physical Review Letters, 2008, 100(20):207402. doi: 10.1103/PhysRevLett.100.207402 [15] TAO H, LANDY N I, BINGHAM C M, et al. A metamaterial absorber for the terahertz regime:Design, fabrication and characterization[J]. Optics Express, 2008, 16(10):7181-7188. doi: 10.1364/OE.16.007181 [16] DAYAL G, RAMAKRISHNA S A. Design of multi-band metamaterial perfect absorbers with stacked metal-dielectric disks[J]. Journal of Optics, 2013, 15(5):527-535. [17] RUFANGURA P, SABAH C. Dual-band perfect metamaterial absorber for solar cell applications[J]. Vacuum, 2015, 120(B):68-74. [18] SHAN Y, CHEN L, SHI C, et al. Ultrathin flexible dual band terahertz absorber[J]. Optics Communications, 2015, 350:63-70. doi: 10.1016/j.optcom.2015.03.072 [19] MO M M, WEN Q Y, CHEN Zh, et al. Strong and broadband terahertz absorber using SiO2-based metamaterial structure[J]. Chinese Physics, 2014, B23(4):589-592. [20] MA R K, ZHANG Y Ch, FANG Y T. Broadband THz absorbers based on graphene and 1-D photonic crystal. Laser Technology, 2017, 41(5):723-727(in Chinese). [21] YAO G, LING F, YUE J, et al. Dynamically electrically tunable broadband absorber based on graphene analog of electromagnetically induced transparency[J]. IEEE Photonics Journal, 2017, 8(1):1-8. [22] CHENG Y Zh, YANG H L, CHENG Zh Z, et al. A planar polarization-insensitive metamaterial absorber[J]. Photonics and Nanostructure-Fundamentals and Applications, 2011, 9(1):8-14. [23] REN Y H, DING J, GUO Ch J, et al. Design of a quad-band wide-angle microwave metamaterial absorber[J]. Journal of Electronic Materials, 2017, 46(1):370-376. doi: 10.1007/s11664-016-4852-3 [24] ZHAI H Q, ZHAN Ch H, LIU L, et al. A new tunable dual-band metamaterial absorber with wide-angle TE and TM polarization stability[J]. Journal of Electromagnetic Waves and Applications, 2015, 29(6):774-785. doi: 10.1080/09205071.2015.1024335 [25] LIU D, YU H T, YANG Zh, et al. Ultrathin planar broadband absorber through effective medium design[J]. Nano Research, 2016, 9(8):2354-2363. doi: 10.1007/s12274-016-1122-x -
点击查看大图
图(5)
计量
- 文章访问数: 6850
- HTML全文浏览量: 4447
- PDF下载量: 144
- 被引次数: 0
