Study on phase difference of all-optical logic XOR gates
-
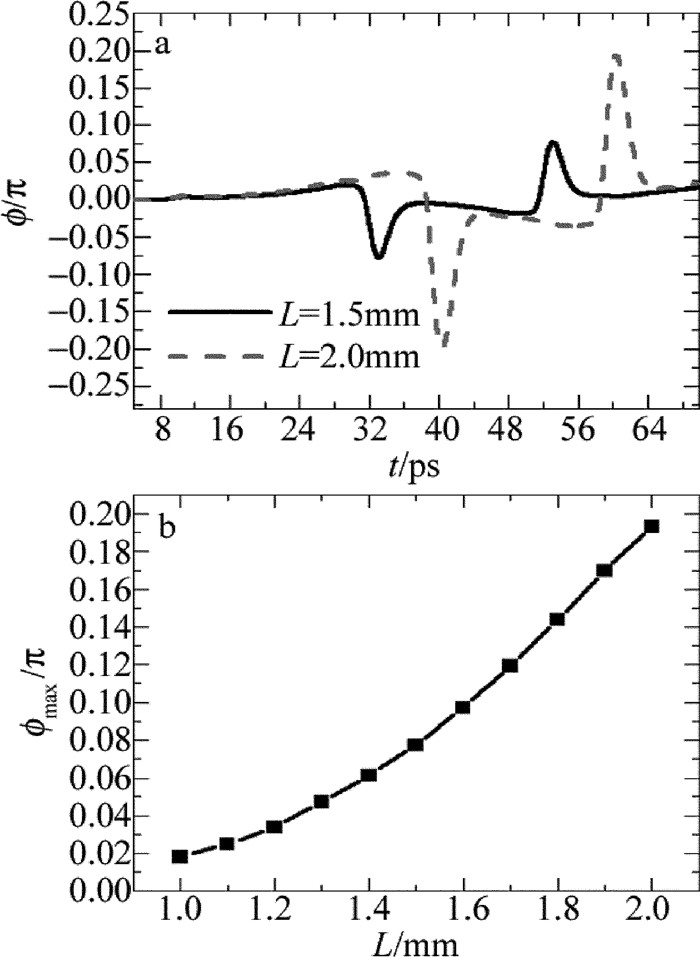
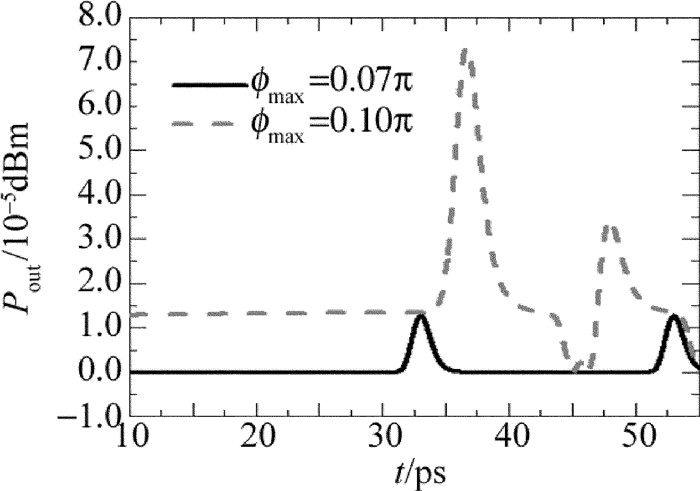
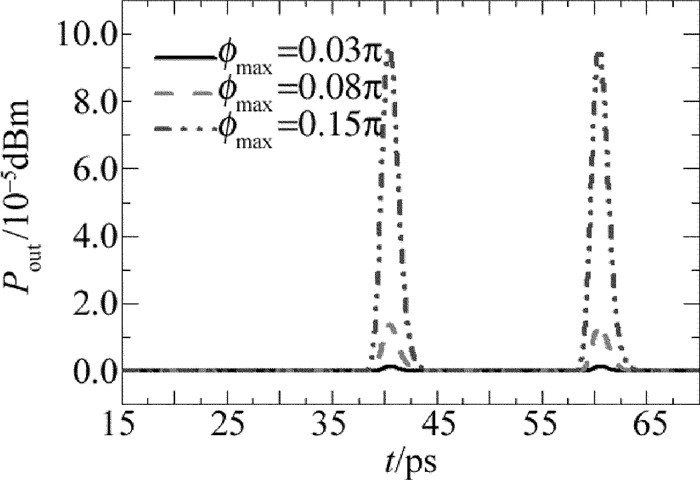
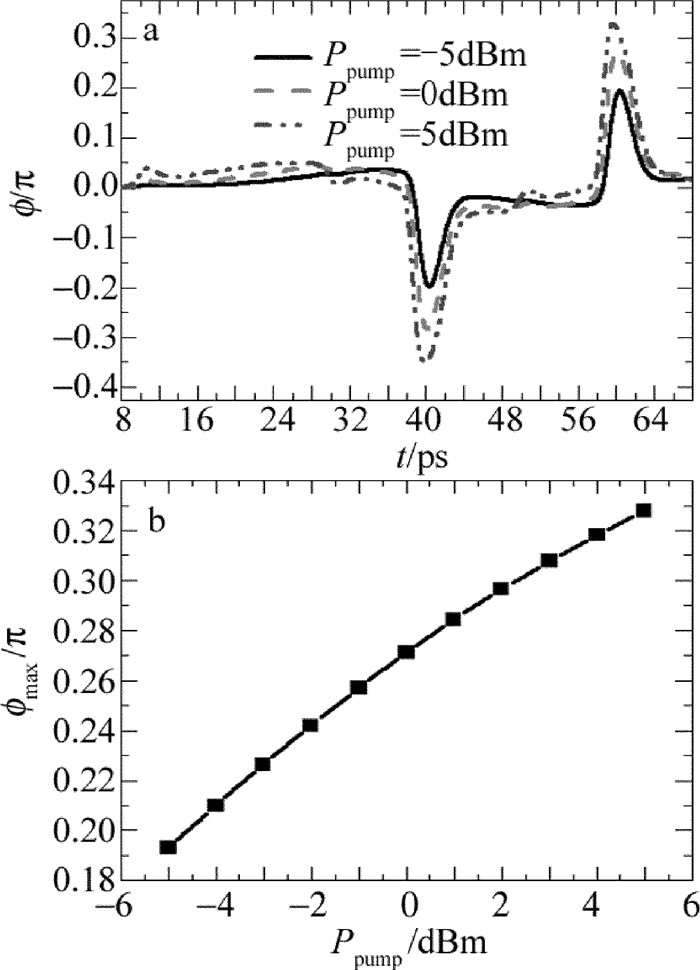
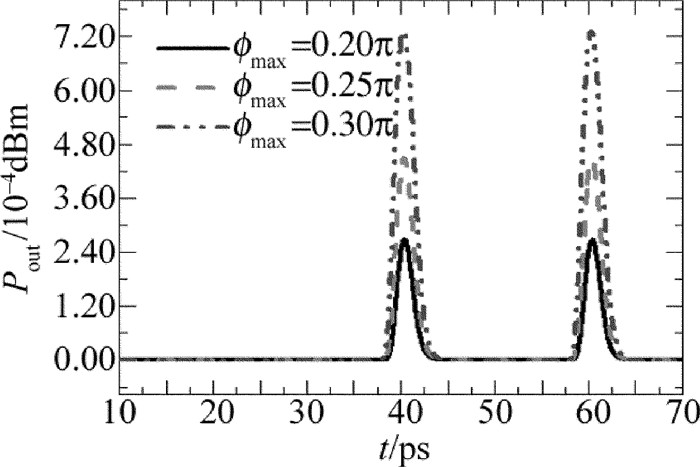
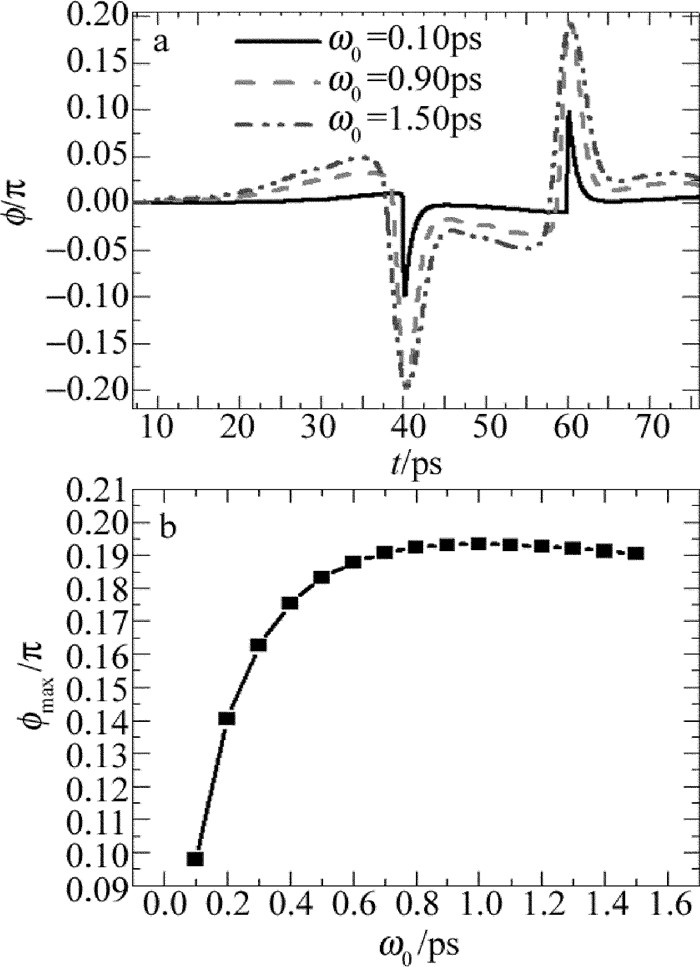
摘要: 为了改善全光逻辑门的相位差特性，对全光逻辑异或门的相位差进行了研究。采用细化分段模型对量子点半导体光放大器的动态过程进行建模，利用牛顿法和4阶龙格-库塔法求解三能级跃迁速率方程以及光场传输方程，实现了基于量子点半导体光放大器马赫-曾德尔干涉仪结构的全光逻辑异或门；研究了有源区长度、最大模式增益、输入抽运光功率以及输入抽运光脉冲宽度对通过干涉仪两臂探测光相位差的影响，同时讨论了探测光的相位差与输出光功率的关系。结果表明，增大有源区长度、最大模式增益以及输入抽运光功率，均能使探测光相位差增大；随着抽运光脉冲宽度增大，探测光相位差先增大而后趋于平缓，之后不断减小；有源区长度为2.0mm、最大模式增益为3000m-1、输入抽运光功率为5dBm、抽运光脉冲宽度为1.0ps时，最大相位差增加至0.3277π；随着探测光相位差增大，输出光功率增大；通过优化参量可以增大探测光的相位差，而输出光功率会随着探测光相位差的增大而增大。该研究为提高转换信号质量提供了参考。
-
关键词:
- 光通信 /
- 量子点半导体光放大器 /
- 异或门 /
- 相位差 /
- 输出光功率
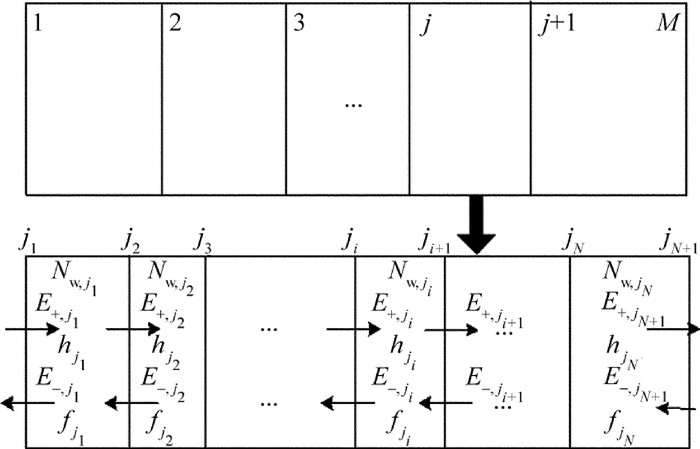
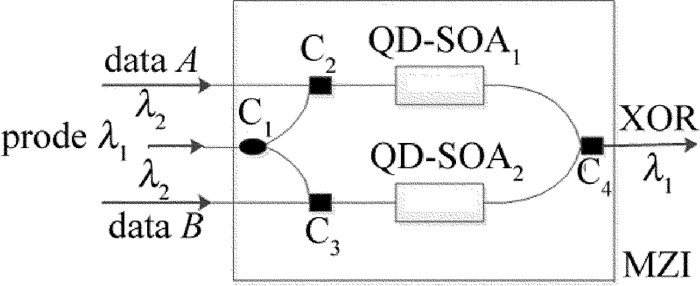
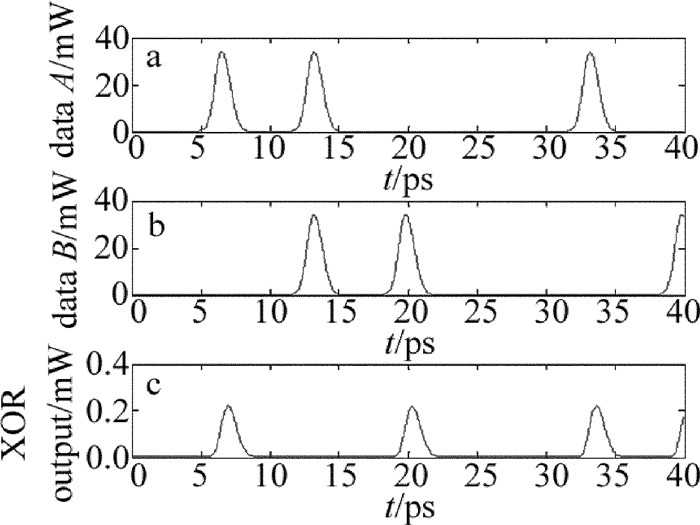
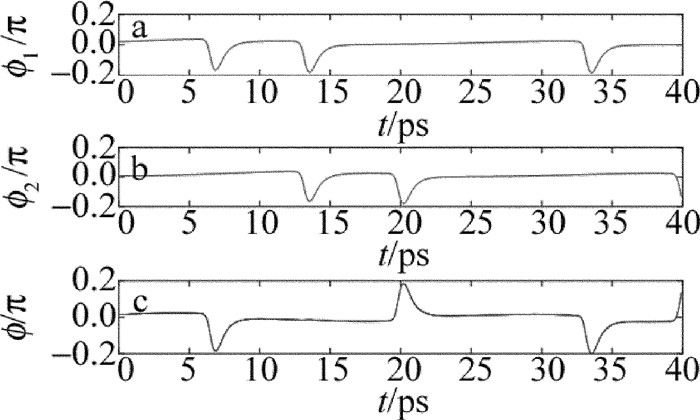
Abstract: In order to optimize the phase difference of the all-optical logic gates, the phase difference of all-optical logic exclusive OR (XOR) gates was studied. Firstly, the refined sectionalized model was used simulate the dynamic process of quantum-dot semiconductor optical amplifier (QD-SOA). Secondly, the Newton method and the four-order Runge-Kutta method were used to solve the three-level transition rate equations and the light field transfer equations. Finally, an all-optical logic XOR gate based on quantum-dot semiconductor optical amplifier Mach-Zehnder interferometer (QD-SOA-MZI) was implemented. The influence of the length of the active regions, the maximum modal gain, input pump power and input pump pulse width on phase difference of probe signal through two arms of the interferometer was studied in detail. Moreover, the relationship between phase difference of the probe signal and output optical power was also discussed. The results show that, with the increase of the length of the active regions, the maximum modal gain and input pump power can lead to improve phase difference of probe signal through two arms of the interferometer. With the increase of input pump pulse width, phase difference of probe signal through two arms of the interferometer increases at first and then decreases. When the length of the active region is 2.0mm, the maximum modal gain is 3000m-1, the input pump power is 5dBm, and input pump pulse width is 1.0ps, the maximum phase difference of probe signal through two arms of the interferometer increases 0.3277π. Output optical power also can be improved by the increase of probe signal phase difference. Phase difference of the detected light can be increased by optimizing the parameters. Output light power increases with the increase of the phase difference of the probe. This study provides a reference for improving the quality of conversion signals. -
-
![]()
Figure 5. Phase of probe signals through two arms of MZI
a—QD-SOA1 b—QD-SOA2 c—phase difference between two arms of MZI
![]()
Figure 6. a—relationship between phase difference and time with different lengths b—relationship between phase difference and length of the active regions
![]()
Figure 8. Relationship between maximum modal gain and phase difference
a—phase difference varying with time in different maximum modal gain b—phase difference varying with maximum modal gain
![]()
Figure 9. Relationship between output optical power and time with different phase differences: 0.03π, 0.08π, 0.15π
![]()
Figure 10. a—relationship between phase difference and time with different pump power b—relationship between phase difference and pump power
![]()
Figure 11. Relationship between output optical power and time with different phase differences: 0.20π, 0.25π, 0.30π
![]()
Figure 12. a—relationship between phase different and time b—relationship between with phase different and pulse width
![]()
Figure 13. Relationship between output optical power and time at different phase differences
Table 2 Parameters for numerical calculation
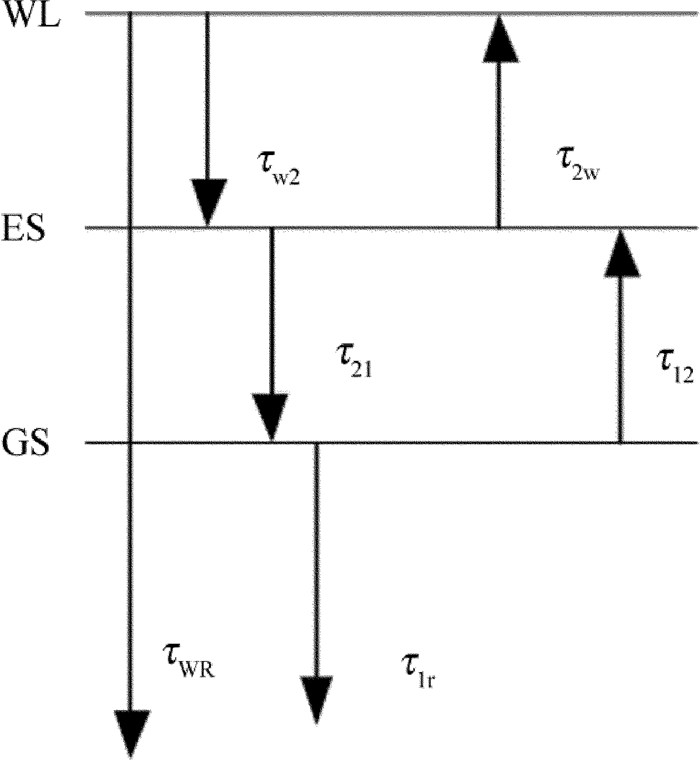
parameter value optical confinement factor Γ 0.5 absorption coefficient of the material αint 300m－1 thickness of wetting layer Lw 0.2μm surface density of QD Nq 5×1014m－2 spontaneous radiative lifetime in QD τ1r 0.4ns spontaneous radiative lifetime in WL τWR 2ns electron escape time from GS to ES τ12 1.2ps electron relaxation time from ES to GS τ21 0.16ps electron escape time from ES to WL τ2w 1ns electron relaxation time from WL to ES τw2 3ps 
下载: 导出CSV
-
[1] CHEN D, WANG R, PU T, et al. A novel thresholder based on XGM effect in a DFB laser combined with external optical filtering[J]. IEEE Photonics Journal, 2016, 8(1): 1-7. http://ieeexplore.ieee.org/document/7393448/
[2] SHI Sh Sh, WANG H L, GONG Q, et al. Refined sectionalized method of QD-SOA[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(1): 504-507. http://www.sciencedirect.com/science/article/pii/S0030402613009649
[3] SINGH P, TRIPATHI D K, JAISWAL S, et al. Designs of all-optical buffer and OR gate using SOA-MZI[J]. Optical and Quantum Electronics, 2014, 46(11): 1435-1444. DOI: 10.1007/s11082-013-9856-0
[4] ZAJNULINA M, LINGNAU B, LVDGE K. Four-wave mixing in quantum-dot semiconductor optical amplifiers: A detailed analysis of the nonlinear effects[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2017, 23(6): 1-12. http://ieeexplore.ieee.org/document/7876839/
[5] KOTB A. Simulation of high quality factor all-optical logic gates based on quantum-dot semiconductor optical amplifier at 1Tb/s[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(1): 320-325. DOI: 10.1016/j.ijleo.2015.10.093
[6] CUI L L, WANG H L, LI W, et al. Study on gain recovery time of wavelength conversion based on single-port-coupled QD-SOA[J]. Laser Technology, 2016, 40(5): 742-745(in Chinese). http://www.jgjs.net.cn/EN/Y2016/V40/I5/742
[7] AMOR L. All-optical networks: Security issues analysis[J]. Journal of Optical Communications and Networking, 2015, 7(3): 136-145. DOI: 10.1364/JOCN.7.000136
[8] TAN H N, INOUE T, SOLIS-TRAPALA K, et al. On the cascadability of all-optical wavelength converter for high-order QAM formats[J]. Journal of Lightwave Technology, 2016, 34(13): 3194-3205. DOI: 10.1109/JLT.2016.2545246
[9] MATAUURA M, OHTA H, SEKI R. Experimental investigation of chirp properties induced by signal amplification in quantum-dot semiconductor optical amplifiers[J]. Optics Letters, 2015, 40(6): 914-917. DOI: 10.1364/OL.40.000914
[10] ALIMOHAMMADI F, YADIPOUR R, ABBASIAN K, et al. THz-assisted instantaneous gain switching in quantum dot semiconductor optical amplifiers[J]. IEEE Photonics Technology Letters, 2015, 27(3): 288-291. DOI: 10.1109/LPT.2014.2369514
[11] EYAL O, WILLINGER A, BANYOUDEH S, et al. Static and dynamic characteristics of an InAs/InP quantum-dot optical amplifier operating at high temperatures[J]. Optics Express, 2017, 25(22): 27262-27269. DOI: 10.1364/OE.25.027262
[12] YANG W H, WANG H L, WANG Zh X, et al.Wavelength conversion efficiency of quantum dot semiconductor optical amplifier[J].Acta Optica Sinica, 2017, 37(4):0406005(in Chinese). DOI: 10.3788/AOS
[13] CHEN T T, WANG H L, LIU S, et al. Theoretical study on chirp of wavelength conversion based on QD-SOA[J]. Laser Technology, 2016, 40(2): 292-295(in Chinese). http://www.opticsjournal.net/abstract.htm?id=OJ1603290001786B9EaH
[14] NURMOHAMMADI T, ABBASIAN K, AS'ADI M J, et al. Design of an ultrafast all-optical NOR logic gate based on Mach-Zehnder interferometer using quantum-dot SOA[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(15): 4023-4029. DOI: 10.1016/j.ijleo.2014.01.119
[15] TALEB H, ABEDI K. Design of a low-power all-optical NOR gate using photonic crystal quantum-dot semiconductor optical amplifiers[J]. Optics Letters, 2014, 39(21): 6237-6240. DOI: 10.1364/OL.39.006237
[16] SINGH P, TRIPATHI D K, DIXIT H K. Designs of all-optical NOR gates using SOA based MZI[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(16): 4437-4440. DOI: 10.1016/j.ijleo.2014.02.032
[17] GAYEN D K, CHATTOPADHYAY T. Designing of optimized all-optical half adder circuit using single quantum-dot semiconductor optical amplifier assisted Mach-Zehnder interferometer[J]. Journal of Lightwave Technology, 2013, 31(12): 2029-2035. DOI: 10.1109/JLT.2013.2263251
[18] GAYEN D K, CHATTOPADHYAY T. Simultaneous all-optical basic arithmetic operations using QD-SOA-assisted Mach-Zehnder interferometer[J]. Journal of Computational Electronics, 2016, 15(3): 982-992. DOI: 10.1007/s10825-016-0854-x
[19] KOTB A, ALAMER F A. Dispersion on all-optical logic XOR gate using semiconductor optical amplifier[J]. Optical and Quantum Electronics, 2016, 48(6): 1-10.
[20] HU Z, XIANG B, XING Y. Optical gain depending on both size fluctuations of quantum dots and temperature in InGaAs/GaAs QD-SOA[J]. IEEE Transactions on Electron Devices, 2017, 64(9): 3683-3689. DOI: 10.1109/TED.2017.2722383
计量
- 文章访问数: 3
- HTML全文浏览量: 1
- PDF下载量: 5