Study on gain characteristics for large-mode-area thulium-doped fibers
-
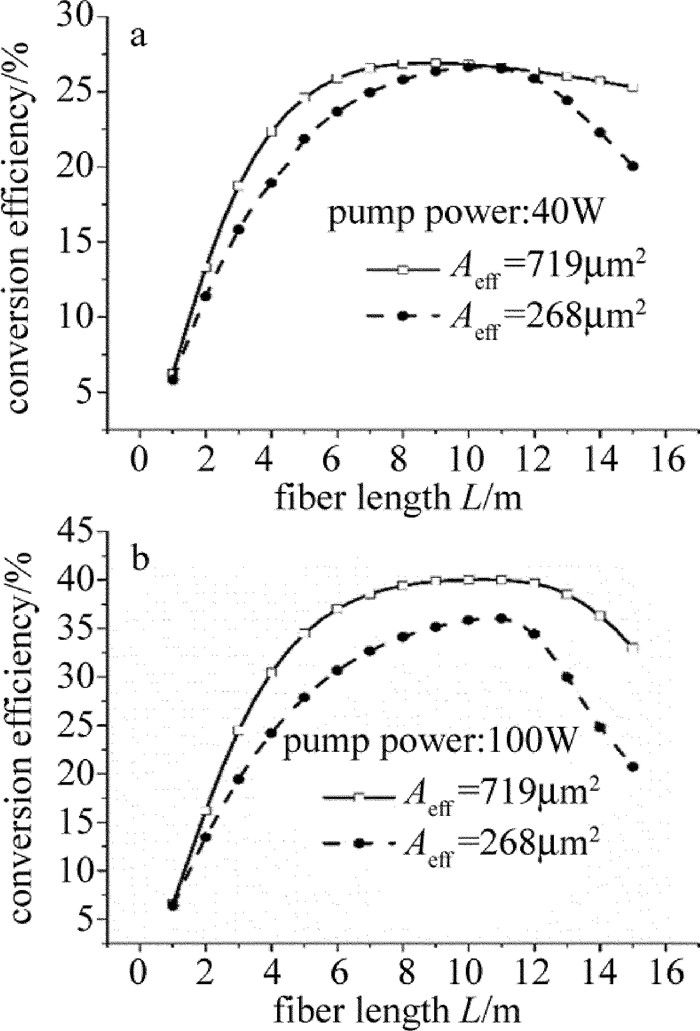
摘要: 为了进一步提升光纤激光器的输出功率，采用大模场面积掺铥光纤来抑制非线性效应，利用非均匀布喇格掺铥光纤结构，通过优化参量，在满足单模传输条件下获得模场面积为719μm2的大模场面积光纤。基于此光纤建立了793nm波长抽运下大模场掺铥光纤放大器理论模型。由于大模场面积光纤能降低光功率密度，抑制Stokes光功率，因此该种光纤放大器在高抽运功率下相比普通单模光纤放大器能够得到更大的输出功率。结果表明，当抽运光功率为100W时，所设计大模场面积光纤与普通单模光纤相比，转换效率提高5%，达到40%，输出功率达到41.01W。以上研究对于实际掺铥光纤放大器的设计有重要应用价值。Abstract: In order to enhance output power of a fiber laser, thulium doped fiber with large mode area was used to suppress the nonlinear effect. Optimizing parameters of a thulium-doped fiber in an inhomogeneous Bragg structure, a fiber with mode area of 719μm2 was obtained under the condition of single-mode transmission. Based on this fiber, a theoretical model for large mode area thulium-doped fiber amplifiers pumped by 793nm wavelength was established. Because large mode area fiber can reduce optical power density and suppress Stokes light power, compared with the ordinary single-mode fiber amplifier, this kind of fiber amplifiers under high pump power can get higher output power. The results show that, when pump power is 100W, compared with the conventional single-mode fiber, the conversion efficiency increases 5% and reaches 40%, and the output power reaches 41.01W. The research is of great value for design of actual thulium-doped fiber amplifiers.
-
-
![]()
Figure 3. Relation between the mode field area and its structure
a—L type mode b—H type mode
![]()
Figure 6. a—the refractive index profile of the outer layer of H-G (ascending) model b—mode field area under change trend of two kinds of refractive index
![]()
Figure 8. Relationship between output power and fiber length with different pump power
a—50W b—100W
![]()
Figure 9. Relationship between amplifier conversion efficiency and fiber length with different pump power
a—40W b—100W
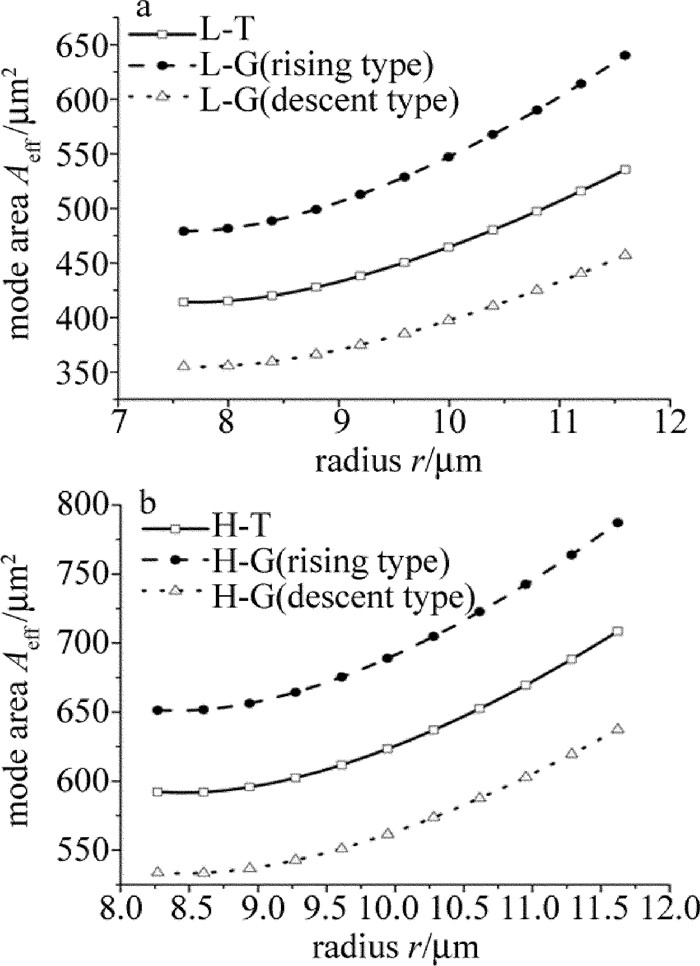
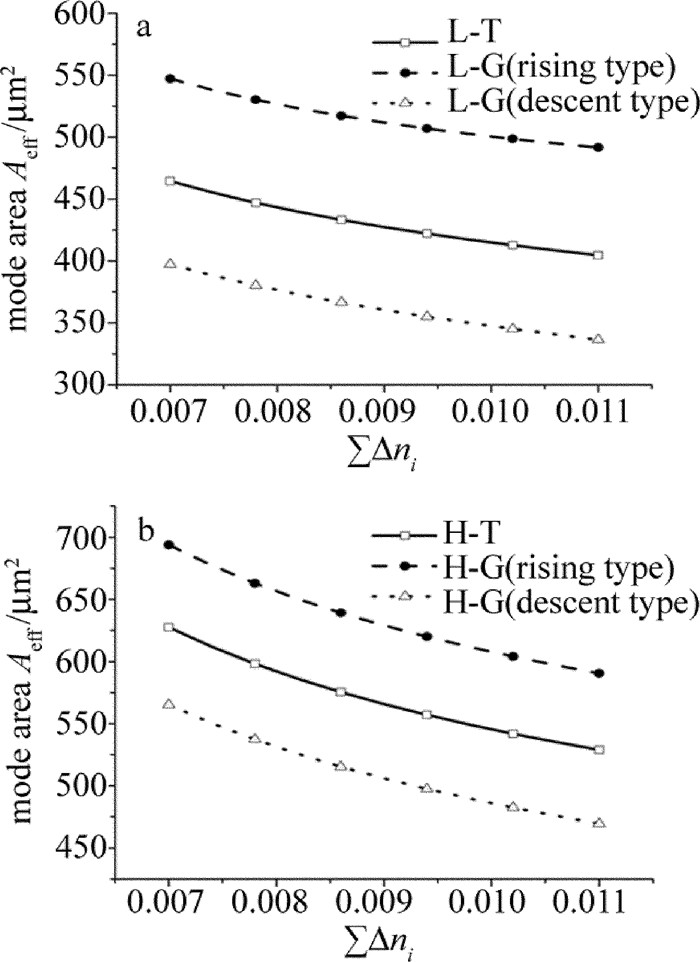
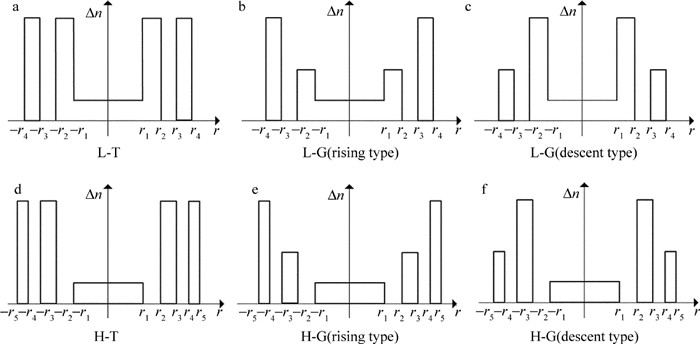
Table 1 Parameters used in structure simulation with r of 10μm
model structure ri/μm Δni L-T (5，7.07，8.66，9.995) (0.001，0.003，0，0.003) L-G(rising type) (5，7.07，8.66，9.995) (0.001，0.002，0，0.004) L-G(descent type) (5，7.07，8.66，9.995) (0.001，0.004，0，0.002) H-T (4.5，6.36，7.79，8.99，10.0) (0.001，0，0.003，0，0.003) H-G(rising type) (4.5，6.36，7.79，8.99，10.0) (0.001，0，0.002，0，0.004) H-G(descent type) (4.5，6.36，7.79，8.99，10.0) (0.001，0，0.004，0，0.002) 
下载: 导出CSV
表 2 Simulation parameters of fiber amplifier
parameter value λp 793nm b 62.5μm σα(λs) 1×10-26m2 σe(λs) 2.5×10-25m2 αs 0.0023m-1 τ1 334.7μs g0 4.0×1011m/W k1013 2.4×10-24m-3·s-1 β30 0.14 νS 34.7GHz λs 2000nm σα(λp) 5.0×10-25m2 σe(λp) 2.18×10-25m2 αp 0.012m-1 N 4.0×1025m-3 τ3 14.2μs ΔνS 58MHz k3101 3×10-23m-3·s-1 β31 0.72 ν0 16.3GHz
下载: 导出CSV
-
[1] GLYBOCHKO P, ALTSHULER G, VINAROV A, et al. Comparison between the possibilities of holmium and thulium laser in lithotripsy in vitro[J]. European Urology Supplements, 2017, 16(3):e391-e392. DOI: 10.1016/S1569-9056(17)30292-0
[2] SENER T E, BUTTICÉ S, MACCHIONE L, et al. Thulium laser vaporesection of the prostate:Can we operate without interrupting oral antiplatelet/anticoagulant therapy?[J]. Investigative & Clinical Urology, 2017, 58(3):192-199. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC5419103/
[3] SCHOLLE K, LAMRINI S, KOOPMANN P, et al. 2μm laser sources and their possible applications[M]. Vukovar, Croatia:Frontiers in Guided Wave Optics and Optoelectronics, 2010:494-495.
[4] ZHANG M, YAN F P, LIU Sh, et al. Research of stimulated brillouin scattering effect in high-power Tm3+-doped fiber amplifiers[J]. Ch-inese Journal of Lasers, 2015, 42(4):0405009(in Chinese). DOI: 10.3788/CJL
[5] LIU J, LIU Ch, SHI H X, et al. 342W narrow-linewidth continuous-wave thulium-doped all-fiber laser. Acta Physica Sinica, 2016, 65(19):194209(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/wlxb201619016
[6] CHANG L P, FAN W, WANG L, et al. Amplification performance of large-and small-mode-area ytterbium-doped double-clad fiber amplifier[J]. Chinese Journal of Lasers, 2007, 34(11):1492-1497(in Ch-inese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgjg200711007
[7] ZHOU D Ch, BAI X M, ZHOU H. Preparation of the large-mode-area ytterbium-doped microstructure fibre and laser performance[J]. Chinese Journal of Lasers, 2014, 41(12):1205006. DOI: 10.3788/CJL
[8] ZHENG J J. Design and fabrication of large-mode-area single mode erbium doped irregular bragg fibers and related devices[D].Beijing: Beijing Jiaotong University, 2011: 73-77(in Chinese).
[9] CAO Zh Q. Transfer matrix method in guided wave optics[M].Shanghai:Profile of Shanghai Jiao Tong University Press, 2000:71-96(in Chinese).
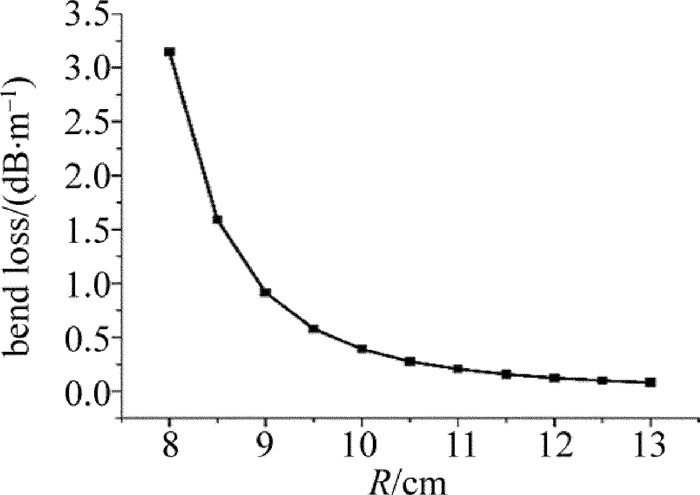
[10] BAGGETT J C, MONRO T M, FURUSAWA K, et al. Understanding bending losses in holey optical fibers[J]. Optics Communications, 2003, 227(4):317-335. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ025163925/
[11] ZHENG S, REN G, LIN Z, et al. Design and analysis of novel multilayer-core fiber with large mode area and low bending loss[J]. Optics Communications, 2014, 315(sC):317-323. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0494ac7f2d2b0d2230a8e7174ef54662
[12] LIN Zh, ZHENG S W, REN G B, et al. Characterization and comparison of 7-core and 19-core large-mode-area few-mode fibers[J]. Acta Physica Sinica, 2013, 62(6):064214(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wlxb201306040
[13] ZHANG W, ZHANG W Y, WU W D, et al. Research progress of high power continuous-wave Tm-doped fiber laser[J]. Infrared, 2017, 38(5):1-7(in Chinese). http://www.en.cnki.com.cn/Article_en/CJFDTotal-HWAI201705001.htm
[14] LONG J Y, BAI J T, REN Z Y, et al. Pumping efficiency analysis and progress of 2μm Tm~(3+) doped silica fiber lasers[J]. Laser Journal, 2009, 30(4):1-3(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgzz200904001
[15] PETERKA P, KASIK I, DHAR A, et al. Theoretical modeling of fiber laser at 810nm based on thulium-doped silica fibers with enhanced 3H4 level lifetime[J]. Optics Express, 2011, 19(3):2773-2781. DOI: 10.1364/OE.19.002773
[16] SMITH A V, SMITH J J. Mode instability thresholds for Tm-doped fiber amplifiers pumped at 790nm[J]. Optics Express, 2016, 24(2):975-992. DOI: 10.1364/OE.24.000975
[17] DONG Sh F, CHENG G F, ZHAO Sh H, et al. Theoretical study on the 1180nm laser pumped Tm, Ho co-doped silica fiber laser[J].Laser Technology, 2006, 30(2):138-141(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs200602009
[18] LI D J, DU G G, YAN P G. Numerical analysis of Tm-doped silica fiber lasers pumped by LD[J]. Journal of Applied Optics, 2007, 28(4):439-444(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yygx200704013
[19] LENG J Y. Theoretical and experimental research on narrow-linewidth fiber amplifiers[D].Changsha: National University of Defense Technology, 2011: 24-26(in Chinese).
[20] WANG Ch C, ZHANG F, LU Y Ch, et al. Study of stimulated brillouin scattering effect in high-power single-frequency fiber amplifiers[J]. Chinese Journal of Lasers, 2006, 33(12):1630-1635(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JJZZ200612011.htm
计量
- 文章访问数: 7
- HTML全文浏览量: 0
- PDF下载量: 6