Line-width measurement of DFB laser based on frequency shift delay self-heterodyning method
-
摘要: 为了测量分布反馈(DFB)单模半导体激光器线宽,采用一种新颖的基于马赫-曾德尔干涉结构的光纤自外差测量方案,设计了一套全光纤延时自外差法测量系统,并进行了理论分析。在此基础上搭建了延时光纤长度分别为900m,3000m和6000m的窄带线宽测量系统,对实验室一台中心波长为1550nm、标称线宽值为800kHz的DFB单模半导体激光器光源进行了测试,测得激光器线宽值分别为951.566kHz,832.471kHz和802.221kHz,并对所设计的方案进行了模拟仿真验证。结果表明,与模拟仿真结果作对比,延时光纤长度为6000m时的窄带线宽测量系统最优,其误差在3%之内,证明了所用自外差干涉原理的合理性和准确性。全光纤移频延时自外差法对测量DFB激光器线宽具有优越性和重要的实用价值。Abstract: In order to measure the line-width of distributed feedback(DFB) diode single mode semiconductor laser, novel optical fiber self-heterodyne measurement scheme based on Mach-Zehnder interference structure was adopted and a set of all fiber time-delay self-heterodyne measurement system was designed. After theoretical analysis, narrow band line-width measurement system with time-delay fiber length of 900m, 3000m and 6000m was set up. A DFB single mode laser source with center wavelength of 1550nm and nominal line-width of 800kHz was tested. The measured line-width values of laser were 951.566kHz, 832.471kHz and 802.221kHz respectively. The designed scheme is verified by simulation. The results show that, compared with the simulation results, narrowband line-width measurement system with the length of 6000m is optimal, and its error is within 3%, which proves the rationality and accuracy of self-heterodyne interference principle. All fiber frequency shift delay self-heterodyne method has advantages and practical value for measuring the line-width of DFB lasers.
-
Keywords:
- laser technique /
- line-width measurement /
- delay self-heterodyne /
- simulation
-
引言
随着激光技术的发展,分布反馈(distributed feedback,DFB)半导体激光器在光学通信[1]、光纤传感技术、信号解调、制导系统和医学等领域有着非常重要的作用,对激光器线宽有着非常高的要求[2]。在如今的许多测试测量系统中,窄线宽的DFB激光器是非常关键的器件。激光器性能的强弱往往是通过对激光器的线宽值的测量来评定的,对于激光器线宽的精确测量,特别是在较窄线宽激光器线宽的测量就尤为重要。
对较窄线宽激光器线宽的测量方法一般是法布里-珀罗干涉仪法与外差法等。如今激光器的线宽已经达到千赫兹量级,对于现有的较窄线宽的激光器线宽参量,上述的法布里-珀罗干涉仪法已经远远无法满足精度要求[3]。光谱线宽的测量方法大致有3种:光谱仪测量法、法布里-珀罗干涉法、拍频法[4]。光谱仪的最小可测带宽为100GHz,法布里-珀罗干涉法的最小带宽为100MHz,而拍频法的最小带宽则已达到100kHz。拍频法中有零差法和外差法,其中最常用的方法是延时外差法,此方法最早是由东京大学的OKOSHI等人最先提出的。外差法是把参考光与信号光干涉后产生拍频信号,由频谱仪测量拍频信号宽度,得出激光器线宽为半峰全宽(full width at half maximum,FWHM)的一半[5]。在国内,由北京邮电大学的REN等其他学者发明制造出第一长波长红外扫描干涉仪[6]。使用此干涉仪用来测量DFB激光器的线宽,在测量激光器线宽时,此干涉仪的腔长会发生变化,从而腔长相应的产生改变,这样就会形成相长干涉,产生两条干涉条纹。把腔长范围变化依次记录下,根据中心波长的值,可以得出半导体激光器的线宽值。运用此测量方法可以很精确地测量出DFB激光器的光谱线宽。但是,对于线宽值低于1MHz的DFB激光器,上述方法不能够完成对于线宽值的测量。
1990年,TSUCHIDA等学者采用循环增益补偿延时外差法的新方法。一般用来测量DFB激光器线宽大小所使用的延迟外差法,通常会与光纤延迟线的长短密切关联,DFB激光器的线宽越窄,所需要的光纤延迟线就越长。在这种状况下,由上述分析可知,要测量出较窄激光器的线宽,需要使用的光纤延迟线需要100km以上的长度才能实现,很难实现实验装置集成。假如测量量级在10kHz以上的激光器的线宽,则需要的光纤延迟线的长度需几十公里。如果待测激光器的线宽值的测量量级更高,那么光纤延迟线的长度就要达到几百千米甚至上千千米才能实现测量[7]。然而在实际测量中非常麻烦,因为使用的光纤延迟线特长,测量过程中存在着损耗和色散等问题,测量结果不精确,存在很大的误差。
本文中以光纤延时外差法为理论依据,在外差法的基础上采取延时自外差法,在装置上不使用参考激光器,简化了装置,降低成本。和零差法相比,在光路中使用了声光移频器(acousto optic modulator,AOM)。声光移频器使频谱的中心频率从零频移到中高频,避免了低频对DFB激光器线宽和功率谱密度函数关系的干扰,然后对实验数据仿真,使窄线宽的测量成为可能。
1. 移频延时自外差法理论分析
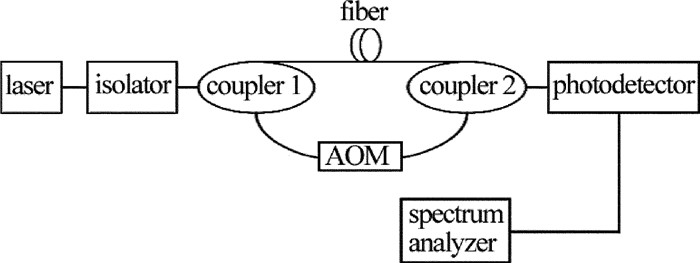
光纤延时自外差法的基本原理是根据全光纤马赫-曾德尔(Mach-Zehnder,M-Z)干涉仪原理,采取不等臂的结构,建立光纤延时外差法的测量系统。延时外差法的原理框架如图 1所示。这是把光的频率噪声转换成强度噪声。先将DFB激光器的输出的光先经过一个光纤隔离器[8]进入1×2光纤耦合分束器,1×2光纤耦合分束器将光大分为两路:一路作为信号光连接光纤延时线,一路作为参考光连接声光移频器(AOM)。参考光和信号光在光纤合束器上互相干涉后得到拍频信号,拍频信号经光电探测器将光信号转换为电信号,最后在频谱仪上展现出功率谱,从而来确定DFB激光器的线宽。延时外差法测量激光器线宽要求延迟时间要大于激光器的相干时间,延迟时间一般情况需大于6倍的相干时间。这样就可以保证整个测量系统的稳定性。
对于理想单色光光源,单纵模激光是一个存在相位扰动和振幅稳定的准单色电磁场[9-10],即:
E(t)=E0exp{j[ω0t+φ(t)]} (1) 式中,E0为光扰动振幅,ω0为电磁场的中心频率,φ(t)为光扰动相位的随机波动,谱线展宽由它导致。采取光纤延时外差法来表示其合成场强[11],即:
Er(t)=E(t)+aE(t+τ0) (2) 式中,a为两束光之间的分光振幅比例,τ0为光纤延时线产生的延时时间,下标r表示电荷到观察点的距离。因为光电探测器的平方率原因,它的强度噪声是由相位的随机波动转换而成,反映的变化就是光电流的频谱展宽[12]。这里,引入光电流自相关函数R1(τ)把单纵模激光线宽和光电流的频谱联系起来,光电流自相关函数是由(2)式所控制的总合成场的强度相关函数来决定的[13],即:
R1(τ)=eσGET(2)(0)δ(τ)+σ2GET(2)(τ) (3) 式中,e是电子电荷,σ是光电探测器的灵敏度,δ是δ函数,GET(2)(τ)是第1阶的光电流强度函数,上标(2)表示原函数的2阶导数,ET表示电场强度,下标T为磁通量密度,此函数的相关函数定义,即:
GET(2)(τ)=ET(t)ET∗(t)ET(t+τ)ET∗(t+τ) (4) 式中,ET*(t)是取共轭。将(2)式代入(4)式中进行简化,即:
Δφ(t,τ)=φ(t+τ)−φ(t) (5) 式中,Δφ(t, τ)是相位随机变化的值,在很多情况下,此相位的随机变化是可以假设成为平稳的高斯随机过程[14],即:
exp[±jΔφ(t,τ)]=exp[−12Δφ2(t)] (6) 同时,相位的相关性可以改写,即:
⟨φ2(τ)⟩=2γ|τ| (7) 式中,2γ是激光器输出谱线的半峰全宽。定义τ=2γτ,τ0=2γτ0,以及θ=ω0τ0= ω0τ0表明了两束光之间的相位差别,ω0为电磁场中心频率的偏移量,τ0为光纤延时时间的偏移量。经过推导可以得到:
GET(2)E40=[(1+a2)+2acosθexp(−¯τ02)]2,(−∞<ˉτ<∞) (8) GET(2)(ˉτ)E40=−4a2exp(−¯τ0)×{sinh(|ˉτ|−¯τ0)+cos2θ[1−exp(|ˉτ|−¯τ0)]},(0<ˉτ<¯τ0) (9) 由著名的维纳-辛钦(Wiener-Khintchine)公式可知,根据把光电流的自相关函数进行傅里叶变换,就可以得出光电流谱密度函数。所以根据(3)式、(8)式和(9)式可以得出:
\begin{array}{*{20}{c}} {\frac{{{S_1}\left( \omega \right)}}{{{\sigma ^2}E_0^4}} = {{\left[ {1 + {a^2} + 2a\cos \theta \exp } \right]}^2}\delta \left( {\bar \omega } \right) + }\\ {4{a^2}\exp \left( { - \overline {{\tau _0}} } \right)\frac{1}{{{\rm{ \mathsf{ π} }}\left( {1 + {{\bar \omega }^2}} \right)}} \cdot }\\ {\left\{ {{\rm{ch}}\overline {{\tau _0}} - \cos \left( {\overline \omega \overline {{\tau _0}} } \right) + {{\cos }^2}\theta \times } \right.}\\ {\left. {\left[ {\cos \left( {\overline \omega \overline {{\tau _0}} } \right) - \frac{{\sin \left( {\overline \omega \overline {{\tau _0}} } \right)}}{{\bar \omega }} - \exp \left( { - \overline {{\tau _0}} } \right)} \right]} \right\}} \end{array} (10) 式中,ch为双曲函数中的双曲余弦,ω为被测信号角速度偏移量。从上式可知,当延迟时间变小时,能量向显示相干性的第1项δ函数集中,该光路系统就会退化成M-Z干涉仪;当延时线变长时,能量就向体现相干性的第2项转移,它的半峰全宽是4γ,是被测激光器线宽的2倍[15],光的相拍特征就由光的相干性转化而来。
考虑声光移频器exp(±jΩt)移频影响,可以得出:
{E_T}\left( t \right) = E\left( T \right) + aE\left( {t + {\tau _0}} \right)\exp \left( {{\rm{j}}\mathit{\Omega }t} \right) (11) 将(11)式带入(4)式中,并作上述相同的简化可得到:
\begin{array}{*{20}{c}} {\frac{{{S_1}\left( \omega \right)}}{{{\sigma ^2}E_0^4}} = {{\left( {1 + {a^2}} \right)}^2}\delta \left( {\bar \omega } \right) + {a^2}\exp \left( { - \overline {{\tau _0}} } \right)\delta \left( {\bar \omega - \mathit{\bar \Omega }} \right) + }\\ {{a^2}\exp \left( { - \overline {{\tau _0}} } \right)\frac{1}{{{\rm{ \mathsf{ π} }}\left[ {1 + {{\left( {\bar \omega - \mathit{\bar \Omega }} \right)}^2}} \right]}} \cdot }\\ {\left\{ {\exp \left( {\overline {{\tau _0}} } \right) - \frac{{\sin \left[ {\left( {\bar \omega - \mathit{\bar \Omega }} \right)\overline {{\tau _0}} } \right]}}{{\bar \omega - \mathit{\bar \Omega }}} - } \right.}\\ {\left. {\cos \left[ {\left( {\bar \omega - \mathit{\bar \Omega }} \right)\overline {{\tau _0}} } \right]} \right\}} \end{array} (12) 式中,Ω是声光移频器带有的移频频率,Ω为声光移频器移频频率的偏移量,a是两束光之间的分光振幅之比。光电流谱密度图中的半峰全宽的1/2就是所测激光器的线宽值。所以本文中可以通过测量拍频谱的半峰全宽得到激光器的实际线宽[16]。
2. 延时自外差法仿真及实验对比
由上述分析延时外差法的原理可得到光电流功率谱密度的函数表达式。考虑对硬件条件的要求,实验中采用短光纤法来测量激光器线宽,这样对数据处理可能不方便,但对硬件设备要求不会很苛刻,不需要外置的保偏器件,减少了长光纤带来的损耗,测量数据也能灵活处理。
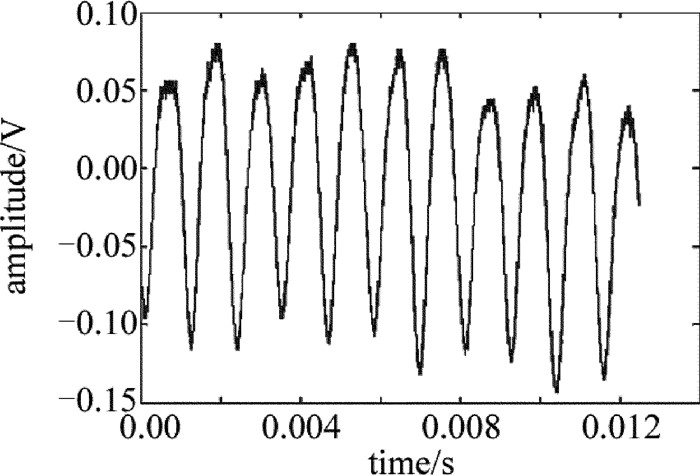
假设待测DFB半导体激光器的中心波长λ=1550nm,线宽Δν=800kHz,则依照前面的分析,该信号在时域内表现为受随机相位调制的余弦曲线,不妨设该光源的光场分布为:
E\left( t \right) = \cos \left[ {2{\rm{ \mathsf{ π} }}{\nu _0} + \varphi \left( t \right)} \right] (13) 式中,ν0=c/λ=1.9355×1014Hz,为待测线宽的光源输出固定频率;φ(t)均匀分布在[-π, π]区间内。
在时域中,因为相位φ(t)是一个随机的变量,因此它的光场分布也有随机性。单色光的时域图像如图 2所示。只有把此信号从时域中转换到频域中,才能得到所需的性能特性[17-18]。
由上述原理分析可以知道,光源功率谱密度曲线应为标准的洛伦兹型分布曲线。它的半峰全宽就是此线宽的2倍,而且此光谱带中心就是光频。
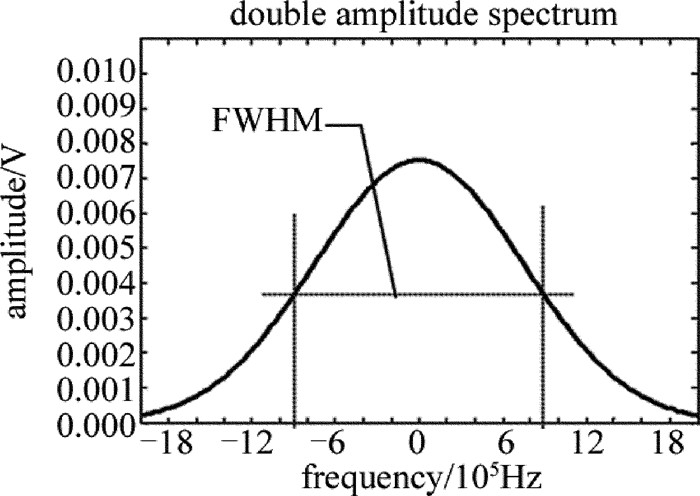
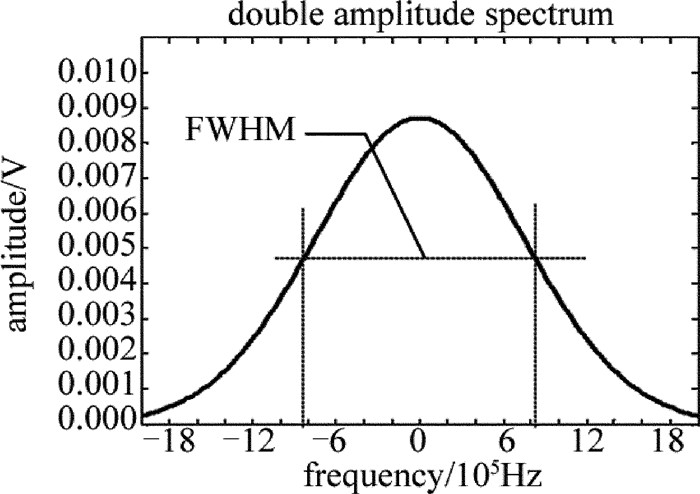
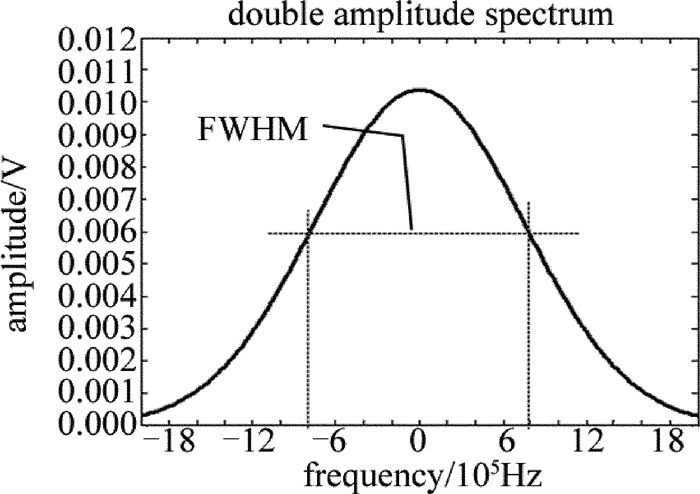
本文中待测光源线宽Δν=800kHz,以300m光纤延迟线为开始,采用上述的原理方法获得光功率谱密度曲线, 得到DFB激光器线宽的测量值ν′,然后每间隔300m记录一组频谱数据,共测量了20组。通过得到的光功率谱密度曲线,得到每一组长度下的测量线宽数值,得到不同光纤延迟线长度下的线宽测量值与DFB激光器线宽实际值之间的关系,如表 1所示。可见,每当光纤延迟线长度增加300m时,DFB激光器的线宽测量值就越接近实际值,当光纤延迟线长度在6000m附近时,测量值与实际值十分接近。
Table 1. Linewidth measurement of light source with linewidth 800kHz at different delay fiber lengthsL/m 300 600 900 1200 1500 ν′/kHz 1414.325 1136.122 951.566 926.318 903.231 L/m 1800 2100 2400 2700 3000 ν′/kHz 883.316 868.719 856.506 844.209 832.471 L/m 3300 3600 3900 4200 4500 ν′/kHz 828.440 820.274 817.669 812.663 809.812 L/m 4800 5100 5400 5700 6000 ν′/kHz 806.375 805.228 804.879 803.849 802.221 从理论解析知,当系统所用光纤延迟线非常短时,则干涉的光程差就非常小,干涉因素对光电流谱密度曲线就有很大影响,使光电流谱密度线型和光源光谱线的偏差就非常大。本文中在20组测量数据中选择长度分别为900m, 3000m和6000m的光纤延迟线作为典型数据,仿真出的光电流谱密度曲线图分别为图 3、图 4和图 5所示。
通过计算可以知道,此时的测量值分别是951.566kHz, 832.471kHz和802.221kHz。由图 3~图 5的功率谱密度曲线变化趋势和计算结果可以很清晰地看出, 当延时光纤的长度在1000m左右时, 所得光源的功率谱密度曲线的线型与理想光源的功率谱密度曲线线型偏差很大, 并且在该长度范围内, 光电流功率谱密度的半峰全宽值随光纤长度的变化极其不稳定。
随着光纤延迟线的延长,测量的线宽与理论线宽值很接近。另外在处理数据的过程中,作者使用的方法非常的简便清晰,产生的误差相对来说也比较小。另一面,延时光纤的长度的变化会对测量有着很大的影响,对于出现不稳定的测量区域应该去除掉。测量时的延时光纤的长度至少要在1000m以上,才能确保测量数据有着相对稳定性和准确性。理论分析中可以得知,使用的延时光纤的长度在6000m左右时,得到的光电流功率谱密度的线性非常接近标准的洛伦兹型曲线,此使得到的激光器的线宽更接近真实值。
3. 结论
本文中建立了光纤延时自外差法的数学模型,测量了DFB激光器线宽,得出功率谱的表达式, 从理论分析与实验验证仿真中得到结果,当光纤延时线足够时,得到的光电流谱密度曲线近似为标准的洛伦兹线型曲线。通过数学工具MATLAB对文中所得到的结果进行了仿真,验证了实验原理和所用方法的正确性。随着激光器产品的迅速发展,所使用的方法也会存在着很多不足。为了能够减少误差而使激光器线宽的测量更加准确,在现有的测量基础上,仍需不断改善测量系统的框架结构,提高测量的精确度。
-
Table 1 Linewidth measurement of light source with linewidth 800kHz at different delay fiber lengths
L/m 300 600 900 1200 1500 ν′/kHz 1414.325 1136.122 951.566 926.318 903.231 L/m 1800 2100 2400 2700 3000 ν′/kHz 883.316 868.719 856.506 844.209 832.471 L/m 3300 3600 3900 4200 4500 ν′/kHz 828.440 820.274 817.669 812.663 809.812 L/m 4800 5100 5400 5700 6000 ν′/kHz 806.375 805.228 804.879 803.849 802.221 -
[1] WANG H X, CHEN J D, CHANG T Y, et al. Research of modulation characteristics of distributed feedback laser[J]. Laser Technology, 2017, 41(6):836-840(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS201706014.htm
[2] WEI Zh P. Narrow linewidth laser spectral width measurement based on time delay self-heterodyne method[J]. Optics and Optoelectronics Technology, 2015, 13(3):38-40(in Chinese).
[3] JIA Y D, OU P, YANG Y H, et al. Short fiber delay self heterodyne method to measure linewidth of narrow linewidth laser[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5):568-571(in Chinese).
[4] PENG J X. Research on narrow linewidth laser linewidth measurement system[D].Beijing: Beijing University of Posts and Telecommunications, 2015: 2-3(in Chinese).
[5] OKOSHI T, KIKUCHI K, NAKAYAMA A. Novel method for high resolution measurement of laser output spectrum[J]. Electron Lett-ers, 1980, 16(16):630-631. DOI: 10.1049/el:19800437
[6] WU T, HUI R Q, ZHANG J P, et al. Full-fiber dual-window high-resolution delay self-heterodyne measurement system[J]. Journal of Beijing University of Posts and Telecommunications, 1990, 13(2):1-6(in Chinese).
[7] XIE D H, DENG D P, GUO L, et al. Narrow line width laser line width measurement method[J]. Laser & Optoelectronics Progress, 2013, 50(1):10006(in Chinese). http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC029715747/
[8] HU J B, LI M P. Design of novel tunable semiconductor lasers in optical fiber communication systems[J]. Laser Technology, 2016, 40(2):280-283(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201602027
[9] FENG S Ch. Multiwavelength single longitudinal mode fiber laser[D]. Beijing: Beijing Jiaotong University, 2010: 111-116(in Chin-ese).
[10] HAN M, WANG A. Analysis of los-compensated recirculating delayed self-heterodyne interferometer for laser linewidth measurement[J]. Applied Physics, 2005, B81(23):53-58. DOI: 10.1007/s00340-005-1871-9
[11] YU B L, YANG J R, YANG Y H, et al. Zero-beat measurement of narrow linewidth laser[J]. Chinese Journal of Lasers, 2001, 28(4):351-354(in Chinese).
[12] DONG Y B. Study of related quantumeffect induced by electromagnetic induced coherent medium[D]. Taiyuan: Shanxi University, 2006: 39-45(in Chinese).
[13] SUN X H. Single longitudinal mode fiber laser and its linewidth measurement[D]. Beijing: Beijing Jiaotong University, 2008: 40-52(in Chinese).
[14] CAO Ch Y, YAO Q, RAO W, et al. Measurement of linewidth of unbalanced fiber interferometer with narrow linewidth laser[J]. Chinese Journal of Lasers, 2011, 38(5):508005(in Chinese). DOI: 10.3788/CJL
[15] ZHOU W, CHONG K M, GUO H. Linewidth measurement of Littrow structure semiconductor laser with improved methods[J]. Physics Letters, 2008, A372(23):4327-4332. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2029e1ff971c96f6c2504e0f8aa150fd
[16] XIAO H J, WANG X, MA Y, et al. Linewidth measurement of na-rrow-linewidth fiber laser based on DSHI[J].Opto-Electronics Engineering, 2010, 37(8):57-61(in Chinese).
[17] LIU J W, DU Zh H, GAO D Y, et al. Research on the dynamic characteristics of semiconductor laser tuning[J]. Laser Journal, 2012, 32(6):6-10(in Chinese).
[18] GAO D Y. Research and instrument development of quasi-continuous tuning laser absorption spectroscopy[D]. Tianjin: Tianjin University, 2011: 21-25(in Chinese).
-
期刊类型引用(8)
1. 陈东升. 基于可见光通信及RFID技术的智能车联网系统设计. 激光杂志. 2023(01): 179-183 .  百度学术
百度学术
2. 崔明斌,黄俊刚,杨修伦. 激光线宽测量方法的研究综述. 激光与光电子学进展. 2021(09): 70-97 .  百度学术
百度学术
3. 宋华峣,王辉林,曹泉泉,张守宇,秦正健. 传递函数快速相关法的激光测速技术研究. 激光技术. 2020(01): 61-65 .  本站查看
本站查看
4. 王翀,磨建业,王景华,杜欢,王璐. X波段光纤延迟线光纤分系统的设计与实现. 光电子·激光. 2020(08): 794-799 .  百度学术
百度学术
5. 王峙清,芦立华. 虚拟现实技术在平面广告视觉优化中的应用研究. 现代电子技术. 2020(24): 149-151+155 .  百度学术
百度学术
6. 蒋金宏,李勇奇,吕欢祝,金琪,张克非. 基于DFB激光器的楔形截顶光纤微透镜耦合结构. 激光技术. 2019(05): 65-69 .  本站查看
本站查看
7. 王晓冬,吴来磊,邢满荣,纪春明. 沥青混凝土中激光加热控制技术. 激光杂志. 2019(10): 117-121 .  百度学术
百度学术
8. 杜雨潇,宋凯利. 基于大数据分析的无线多媒体传输系统设计. 自动化与仪器仪表. 2019(10): 34-37+42 .  百度学术
百度学术
其他类型引用(10)



 下载:
下载: