Study on characteristics of neutral strontium atoms based on laser cooling technique
-
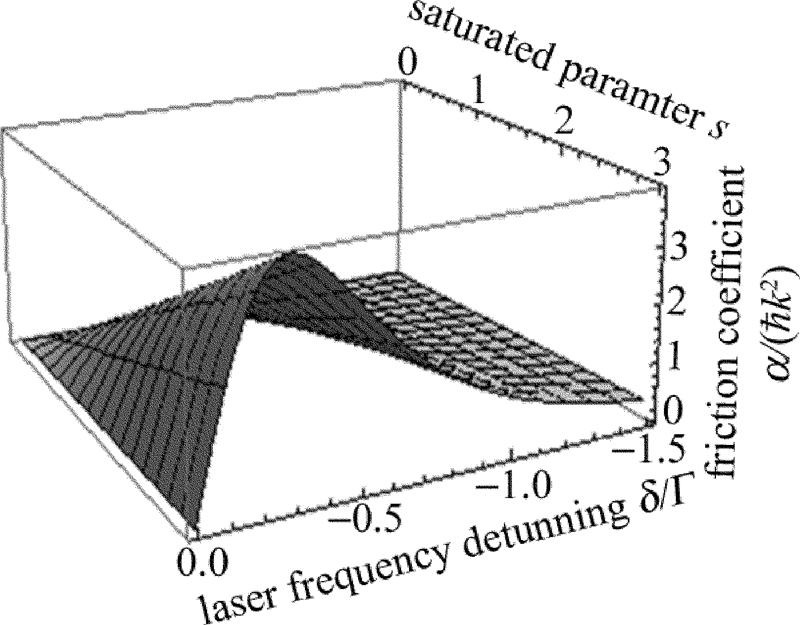
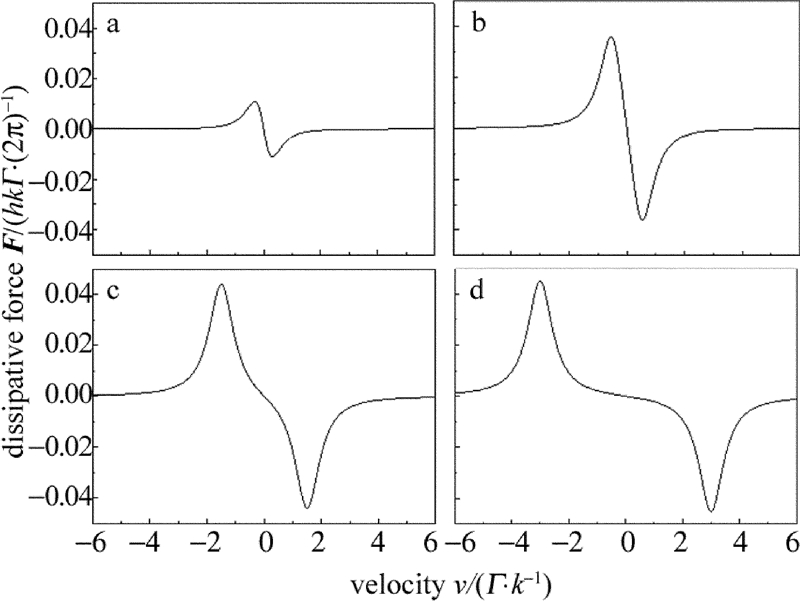
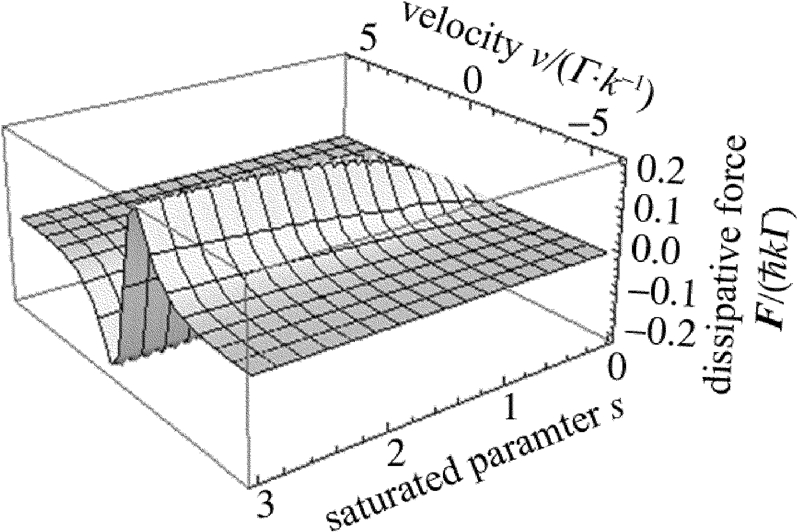
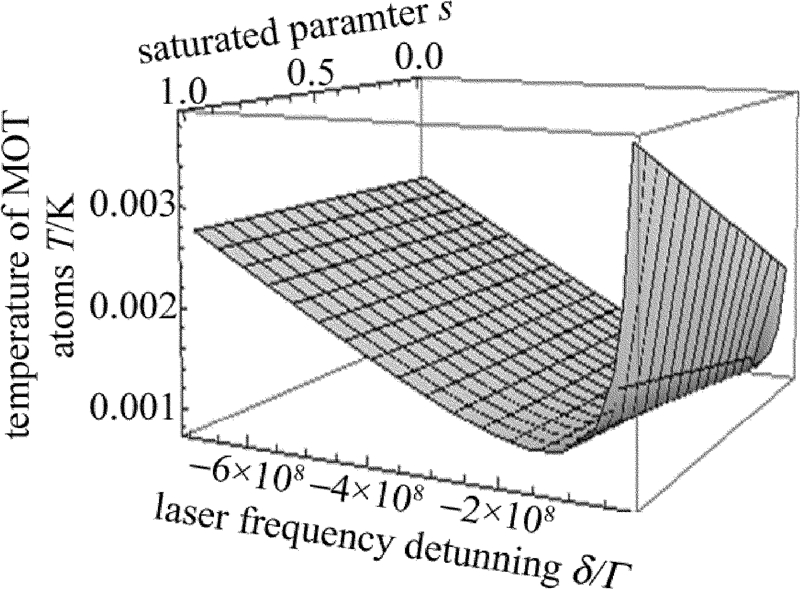
摘要: 为了研究碱土金属类的中性锶原子在多普勒冷却激光场中的冷却特性，从Heisenberg方程出发，采用激光冷却理论分析得到锶原子在能级跃迁（5s2）1S0~（5s5p）1P1 1维驻波激光光场和3维磁光阱中冷却效果与激光强度、失谐量等冷却激光场参量的关系。结果表明，当锶原子处在1维驻波激光光场中且在弱激光光场、频率小失谐条件下，锶原子所受耗散力与这两个参量呈线性关系，但当两个参量增长至一定程度时耗散力呈现饱和现象；当锶原子在3维磁光阱中且当阱中激光光场的频率失谐为-16MHz时，碱土金属锶原子有最低冷却温度，约为0.76mK。对多普勒冷却光场中性锶原子特性的分析为其它碱土金属类原子的冷却研究提供了一定的理论指导。Abstract: In order to study cooling characteristics of neutral Sr of alkaline-earth metal in a Doppler cooling laser field, the relationship between the cooling results of strontium atomic in 1-D laser standing wave light field with energy level transition (5s2)1S0~(5s5p)1P1 and 3-D magneto-optical trap and laser parameters, including laser intensity and frequency detuning, was obtained by using the theory of laser cooling based on Heisenberg equations. The results show that, when the strontium atoms are in 1-D standing wave laser field and under the condition of weak laser field and frequency detuning, the dissipation force of strontium atoms is linearly related to the two parameters. But when the two parameters increase to a certain degree, the dissipative force is saturated. When strontium atoms are in 3-D magneto-optical trap and frequency detuning of laser light field in the traps is -16MHz, alkaline-earth metal strontium atoms have the lowest cooling temperature of 0.76mK. The characteristics analysis of neutral strontium atoms in Doppler cooling field provides some theoretical guidance for cooling study on other alkaline-earth metal atoms.
-
-
![]()
Figure 1. Relationship between dissipative force of 1-D laser standing wave and atomic velocity
![]()
Figure 3. Relationship between dissipative force and velocity under different laser frequency detuning
![]()
Figure 4. Relationship between dissipative force and velocity under different laser intensities
-
[1] HANSCH T W, SCHAWLOW A L. Cooling of gases by laser radiation[J]. Optics Communications, 1975, 13(1):68-69. DOI: 10.1016/0030-4018(75)90159-5
[2] CHRISTENSEN B T R, HENRIKSEN M R, SCHAFFER S A, et al. Non-linear spectroscopy of Sr atoms in an optical cavity for laser stabilization[J]. Physical Review, 2015, A92(5):053820. http://arxiv.org/abs/1507.05757
[3] DAREAU A, SCHOLL M, BEAUFILS Q, et al. Doppler spectroscopy of an ytterbium bose-einstein condensate on the clock transition[J]. Physical Review, 2015, A91(2):023626.
[4] GERTIS J, FRIESDORF M, RIOFRIO C A, et al. Estimating strong correlations in optical lattices[J]. Physical Review, 2016, A94(5):053628. http://arxiv.org/abs/1606.01913
[5] WEINER J, BAGNATO V, ZILIO S, et al. Experiments and theory in cold and ultracold collisions[J]. Reviews of Modern Physics, 1999, 71(1):1-85. DOI: 10.1103-RevModPhys.71.1/
[6] USHIJIMA I, TAKAMOTO M, DAS M, et al. Cryogenic optical lattice clocks[J]. Nature Photonics, 2015, 9:185-189. DOI: 10.1038/nphoton.2015.5
[7] LI Y Q, XIONG X M, ZHANG W T. 3-D analysis of laser-cooling Cr atoms[J]. Laser Technology, 2012, 36(6):788-792(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS201206018.htm
[8] WILLIAM D P. Laser cooling and trapping of neutral atoms[J]. Reviews of Modern Physics, 1998, 70(3):721-741. DOI: 10.1103/RevModPhys.70.721
[9] WANG Y Q. Laser cooling and trapping of atoms[M]. Beijing:Peking University Press, 2007:336-383(in Chinese).
[10] BALYKIN V I, LETOKHOV V S, MUSHIN V I. Observation of the cooling of free sodium atoms in a resonance laser field with a scanning frequency[J]. JETP Letters, 1979, 29(10):560-564.
[11] CHU S, HOLLBERG L, BJORKHOLM J E, et al. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure[J]. Physical Review Letters, 1985, 55(1):48-51. DOI: 10.1103/PhysRevLett.55.48
[12] IAN N. Laser cooling and trapping of neutral calcium atoms[D]. Glasgow, UK: University of Strathclyde, 2009: 9-23.
[13] ZHOU M, XU X Y. Advances in the precision spectroscopy of cold ytterbium atoms[J]. Physcis, 2016, 45(7):431-440(in Ch-inese). http://www.en.cnki.com.cn/Article_en/CJFDTotal-WLZZ201607004.htm
[14] LIU H, GAO F, WANG Y B, et al. Precision frequency measurement of 1S0-3P1 intercombination lines of Sr isotopes[J]. Chinese Physics, 2015, B24(1):013201. http://www.cqvip.com/QK/85823A/201501/663382092.html
[15] SORRENTION F, FERRARI G, POLI N, et al. Laser cooling and trapping of atomic strontium for ultracold atoms physics, high-precision spectroscopy and quantum sensors[J]. Modern Physics Letters, 2006, B20(21):1287-1320. DOI: 10.1142/S0217984906011682
[16] MICKELSON P G, MARTINEZ de ESCOBAR Y N, ANZEL P, et al. Repumping and spectroscopy of laser-cooled Sr atoms using the (5s5p)3P2-(5s4d)3D2 transition[J]. Journal of Physics, 2009, B42(23):235001. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0907.2270
[17] WANG S K, WANG Q, LIN Y G, et al. Cooling and Trapping 88Sr atoms with 461nm laser[J]. Chinese Physics Letters, 2009, 26(9):093202. DOI: 10.1088/0256-307X/26/9/093202
[18] TANNOUDJI C C, ODELIN D G. Advances in atomic physics[M]. Singapore City, Singapore:World Scientific Publishing Co.Pte.Ltd., 2011:243-267.
[19] THIERRY C, JEAN-LOUIS M, ROBIN K, et al. Extra-heating mechanism in Doppler cooling experiments[J]. Journal of the Optical Society of America, 2005, B22(9):1819-1828. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_physics%2f0412119
下载:
计量
- 文章访问数: 2
- HTML全文浏览量: 0
- PDF下载量: 6