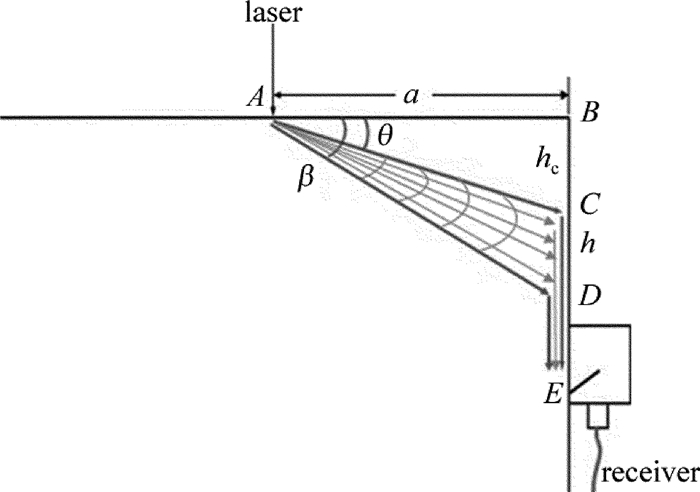
Mode conversion of laser-excited shear waves interaction with the side of vertical cracks
-
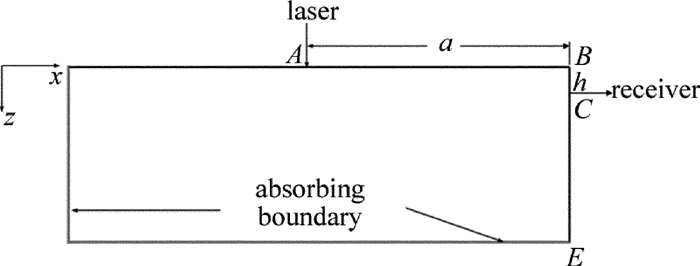
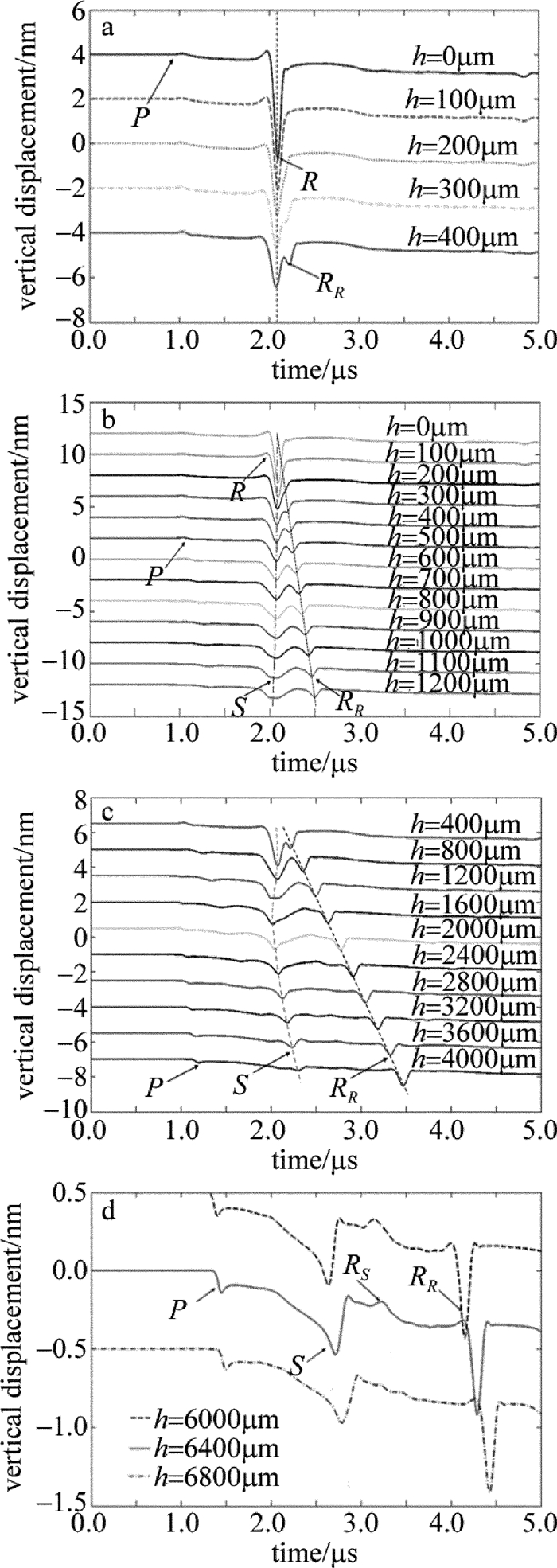
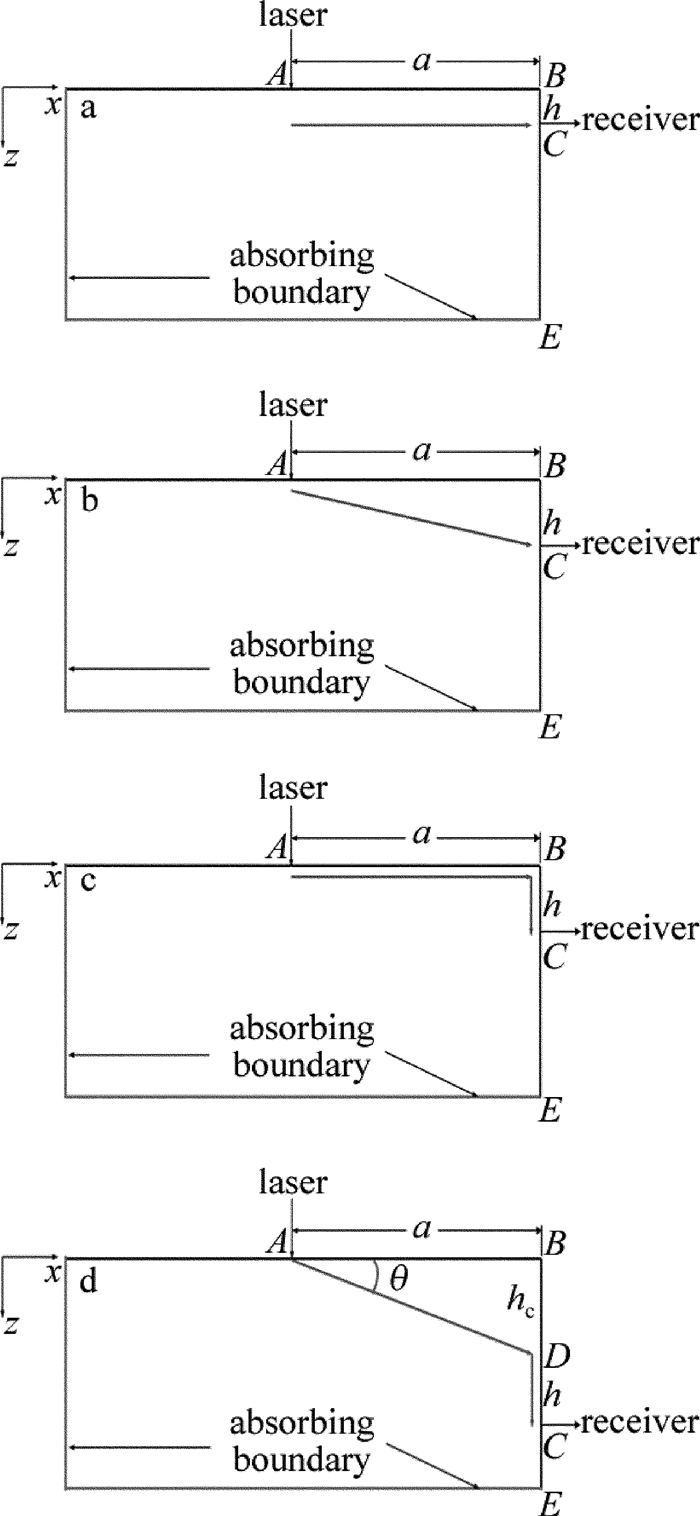
摘要: 为了研究激光激发横波与材料表面垂直裂纹侧面作用所发生模式转换现象，采用有限元法模拟了激光水平激发、垂直侧面接收的声传播及模式转换，并进行了相应的实验验证。分析激光激发超声波传播至垂直侧面时，侧面接收点在不同深度接收位移信号的变化情况。结果表明，当侧面接收点处于临界角对应深度以内时，出现激光激发表面波在拐角次生源处产生的表面波信号；而当侧面接收点处于临界角以外时，在此信号之前出现了经由激光激发横波作用垂直裂纹侧面所产生的模式转换，并形成新的表面波；且对于固定的激发位置，随着接收点位置下移，两种信号之间的到达时差逐渐增大。该结果可促进激光超声对垂直裂纹的检测研究。Abstract: In order to study mode conversion of laser-excited shear waves interaction with the side of vertical cracks, the laser-generated ultrasound propagating along the horizontal surface and received on the vertical surface was simulated by means of finite element method. After experiments, the change of displacement signals received by side receiving point at different depths was analyzed when laser-excited ultrasonic was transmitted to the vertical side. The results show that, when the side receiving point is within the corresponding depth of the critical angle, the surface wave signal generated by laser-excited surface wave at the secondary source of the corner appears. When the side receiving point is outside the critical angle, there is a mode transformation generated by laser-induced shear wave acting on the side of the vertical crack, and a new surface wave is formed. Furthermore, when the excitation position is fixed, time difference of arrival between both signals increases gradually with the downward receiving position. The results can promote the detection of vertical cracks by laser ultrasound.
-
-
![]()
Figure 1. Analysis of reflection characteristics of shear wave at oblique incidence to vacuum interface in solid materials
![]()
Figure 2. Finite element model of waves generated on the horizontal surface and received on the vertical side
![]()
Figure 6. Side reception of surface wave piezoelectric probe corresponding to laser-excited ultrasonic at different positions
![]()
Figure 7. Side reception of surface wave piezoelectric probe corresponding to laser-induced transverse wave at critical angle
Table 1 Material parameters of aluminum for finite element model
Young modulus/GPa Poisson’sratio density/(kg·m-3) specific heat capacity/(J·kg-1·K-1) thermal conductivity/(W·m-1·K-1) thermal expansion coefficient/10-5K absorptivity 70 0.33 2700 900 160 2.3 0.05 
下载: 导出CSV
Table 2 Velocity of waves in aluminum material
vS/(km·s-1) vL/(km·s-1) vR/(km·s-1) 3.080 6.260 2.910
下载: 导出CSV
Table 3 Position of laser excitation and signal reception
laser excitation x/mm critical angle θ/(°) critical depth xtanθ/mm probe position y/mm 30 30 17.3 4.8 40 23.1 10.6 50 28.9 16.4 60 34.6 22.1
下载: 导出CSV
Table 4 Experimental calculation of critical angle of aluminum materials
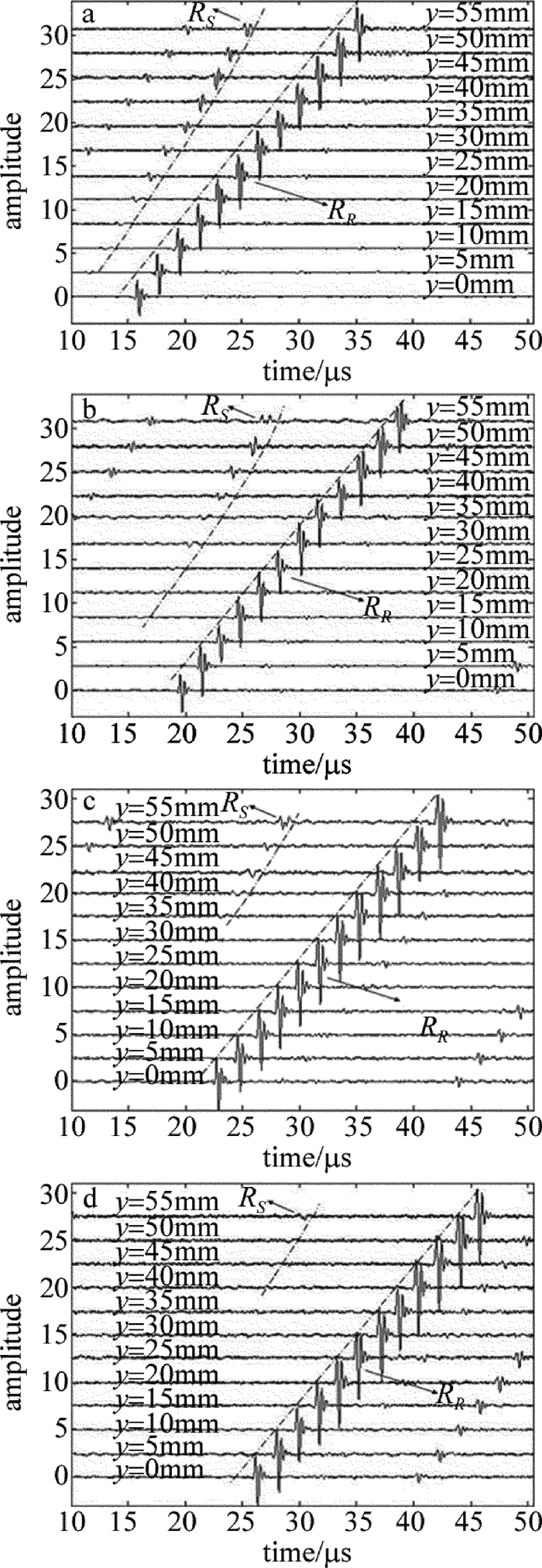
laser excitation x/mm probe position for the first signal RS y/mm critical depth y/mm critical angle θ/(°) 30 5 17.5 30.2 40 15 27.5 34.5 50 30 42.5 40.4 60 40 52.5 41.2
下载: 导出CSV
-
[1] GUAN J F, SHEN Zh H, XU B Q, et al. Spectral analysis of the scattering waveform of the laser-generated ultrasonic waves for detecting the crack in the material[J]. Laser Technology, 2005, 29(3):287-290(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs200503012
[2] WANG W, ZHONG Zh, PAN Y D. Scattered echo of surface defect in the far field of Rayleigh wave generated by laser[J]. Laser Technology, 2015, 39(2):157-165(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201502003
[3] JIAN X, DIXON S, GUO N, et al. Rayleigh wave interaction with surface-breaking cracks[J]. Journal of Applied Physics, 2007, 101(6):064906. DOI: 10.1063/1.2435803
[4] ZHOU Zh G, ZHANG K Sh, ZHOU J H, et al. Application of laser ultrasonic technique for non-contact detection of structural surface-breaking cracks[J]. Optics & Laser Technology, 2015, 73:173-178. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8c971328706d1dc9f74e4fd903ed2f3a
[5] GUAN J F. Numerical study on signal enhancement of the Rayleigh wave in the near-field of surface defects[J]. Japanese Journal of Applied Physics, 2014, 49(6):1212-1219. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10bcb65fbb91bab01013392481edf31f
[6] ZENG W, WANG H T, TIAN G Y, et al. Research on the oscillation effect of near-surface metal defect based on laser-generated acoustic surface wave[J]. Acta Physica Sinica, 2015, 64(13):134302(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/wlxb201513025
[7] GUAN J F, SHEN Zh H, XU B Q, et al. Numerical simulation of laser ultrasonics for detecting subsurface lateral defects[J].Proceedings of the SPIE, 2005, 5629:457-465. DOI: 10.1117/12.572869
[8] LI Y L. Research on laser ultrasonic testing of internal defects in metal materials based on reflected shear wave[D]. Nanjing: Nanjing University of Science and Technology, 2014: 29-39(in Chinese).
[9] LI M. A study on ultrasonic inspection of tyres by transverse waves[J]. Nondestructive Testing, 2000, 22(4):162-164(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wsjc200004005
[10] XU Ch G, LI H X, WANG J F, et al. Ultrasonic shear and longitudinal wave testing method of residual stress[J]. Acta Acustica, 2017, 42(2):195-204(in Chinese).
[11] GUAN J F, SHEN Zh H, NI X W, et al. Numerical analysis of the surface notch inspection by laser generated Rayleigh waves on aluminum plate[J]. Journal of Test and Measurement Technology, 2006, 20(5):390-396(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hbgxycsjsxb200605003
[12] JIAN X, DIXON S, GUO N, et al. Rayleigh wave interaction with surface-breaking cracks[J]. Journal of Applied Physics, 2007, 101(6):064907. DOI: 10.1063/1.2712159
[13] COOPER J A, CROSBIE R A, DEWHURST R J, et al. Surface acoustic wave interactions with cracks and slots:a noncontacting study using lasers[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 1986, 33(5):462-470. http://europepmc.org/abstract/MED/18291810
[14] COOPER J A, DEWHURST R J, PALMER S B, et al. Characterization of surface-breaking defects in metals with the se of laser-generated ultrasound[J]. Philosophical Transactions of the Royal Society of London, 1986, A320(1554):319-328. http://www.jstor.org/stable/37920
[15] ROSE J L. Ultrasonic waves in solid media[M]. Beijing:Science Press, 2004:36-40(in Chinese).
[16] ZHAN Y, XUE J Zh, LIU Ch Sh. Numerical simulation of laser ultrasonic elastic constant measurement based on Abaqus[J]. Chinese Journal of Lasers, 2015, 42(5):0508002(in Chinese). DOI: 10.3788/CJL
[17] JIN L, WANG W, PAN Y D. Theoretical study of the interaction of laser excited surface acoustic waves with subsurface deffects[J]. Chinese Journal of Solid Mechanics, 2017, 38(2):170-179(in Chinese). http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-GTLX201702006.htm
[18] WANG M Y, ZHOU Y J, GUO Ch. Numerical simulation of laser ultrasonic detection of surface micro-crack depth[J]. Laser Technology, 2017, 41(2):178-181(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201702006
[19] LI X X, ZHAO J F, PAN Y D. On the measurement method of material constants based on laser ultrasonic field testing system[J]. Journal of Experimental Mechanics, 2016, 31(3):352-360(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/sylx201603009
计量
- 文章访问数: 5
- HTML全文浏览量: 0
- PDF下载量: 6