High intensity attosecond pulse generated by the improved multi-cycle polarization gating technology
-
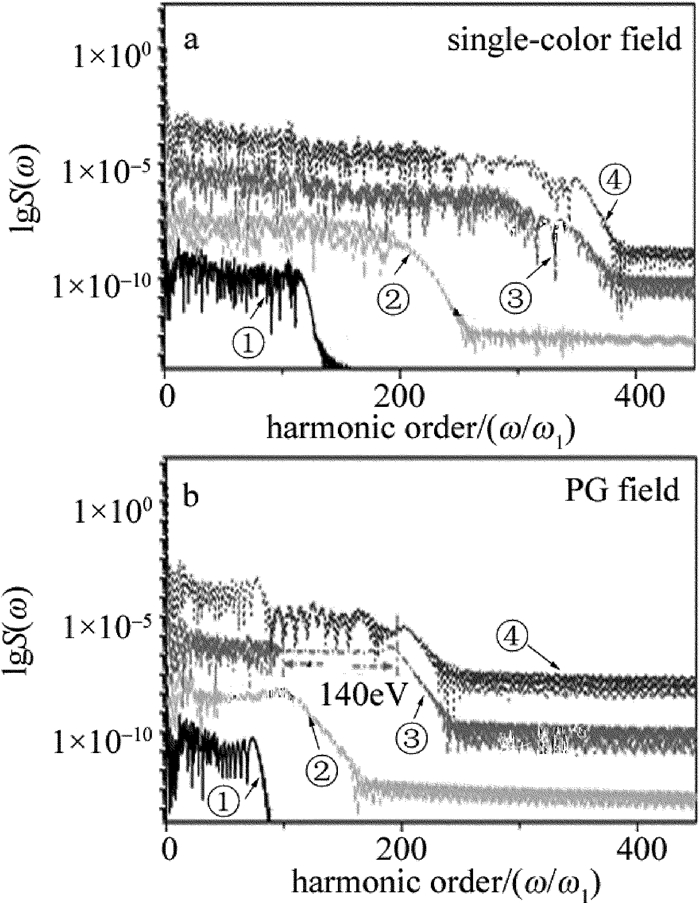
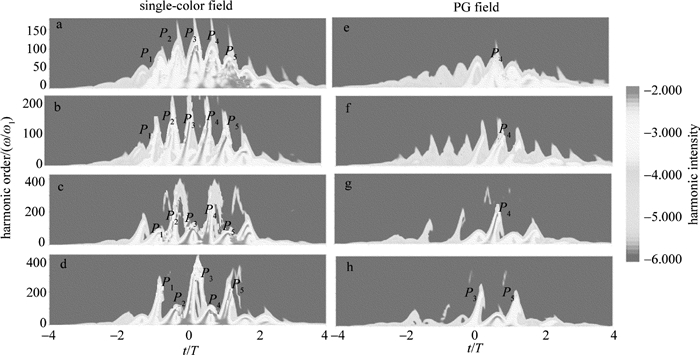
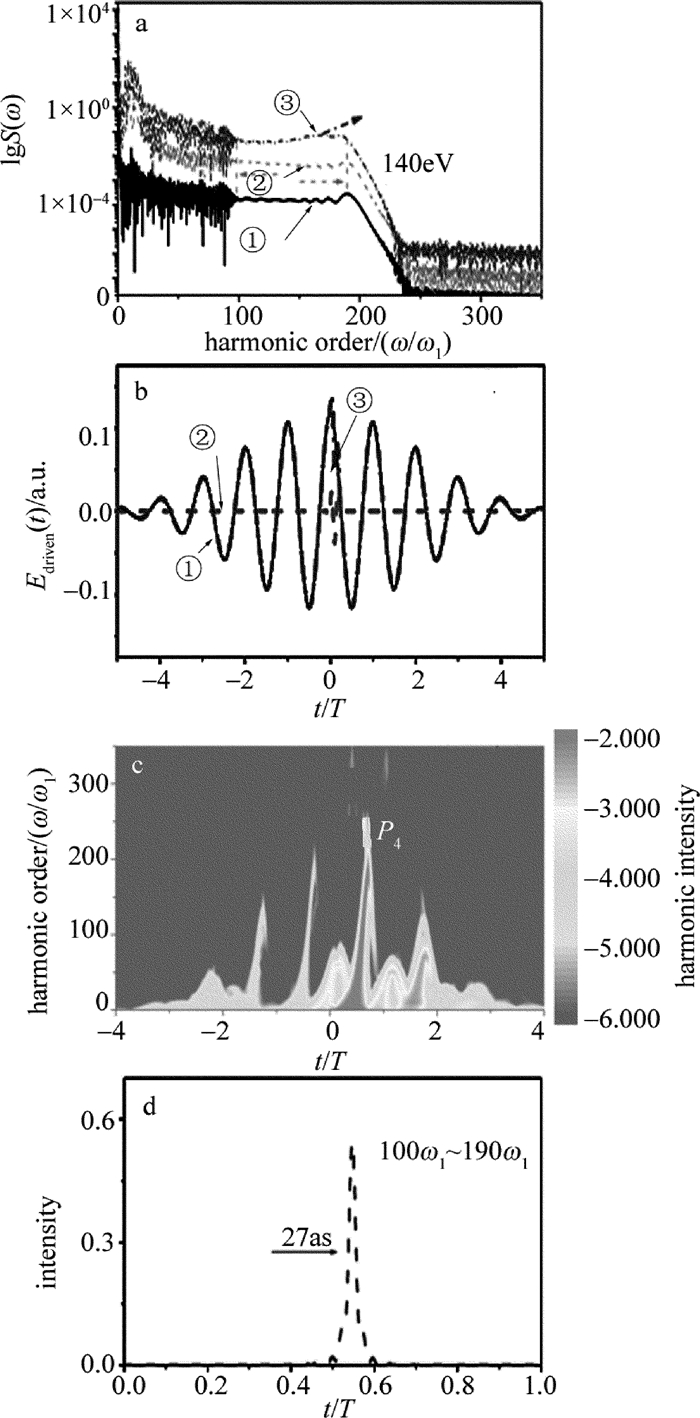
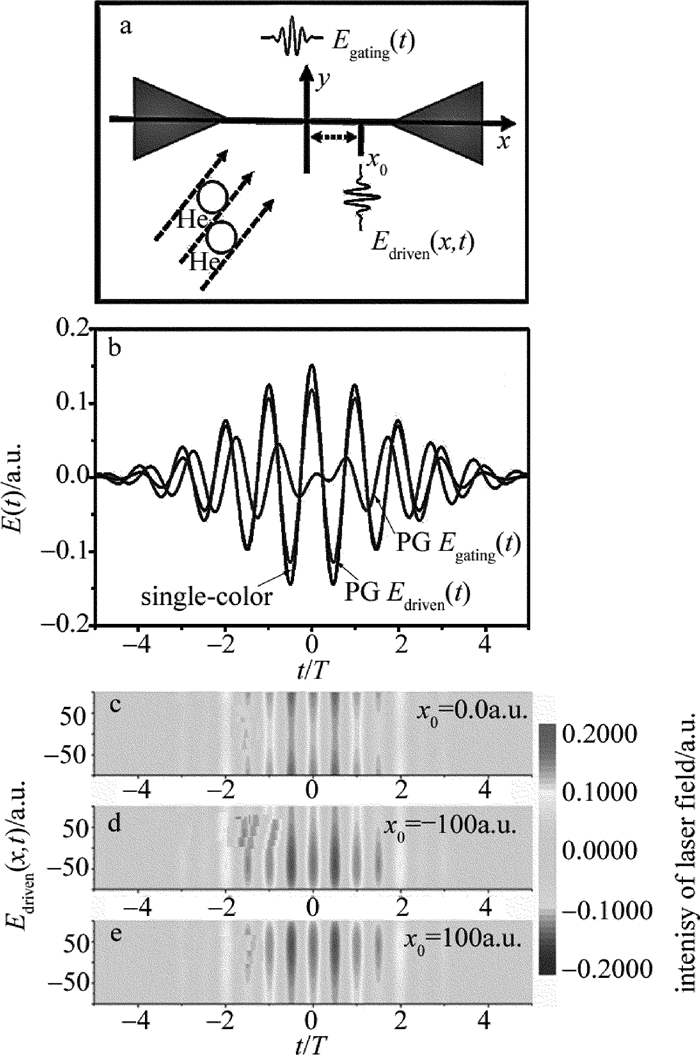
摘要: 为了产生高强度单个阿秒脉冲，采用多周期极化门方案，利用空间非均匀极化门调控谐波辐射，在蝴蝶型纳米结构下产生高强度阿秒脉冲。结果表明，由于纳米结构表面的等离子共振增强现象，激光强度在空间呈非均匀性，导致高次谐波截止能量得到延伸，长量子路径对谐波的贡献被减弱；在极化门控制下，谐波平台区的贡献只来源于单一的谐波辐射能量峰，形成一个140eV的平台区；适当引入一束超短紫外光源，谐波强度增强2个数量级；通过叠加平台区的谐波，可获得一个持续时间在27as的超短脉冲，该脉冲强度比利用单一极化门方案获得的脉冲强度增强2个数量级。该研究对阿秒脉冲的产生以及阿秒科学的发展是有帮助的。Abstract: In order to produce high-intensity single attosecond pulse (SAP), an improved multi-cycle polarization gating (PG) technology was proposed and the inhomogeneous PG scheme was used to control harmonic emission and to produce the SAP in the bowtie-shaped nanostructure. After theoretical analysis and experimental verification, it is found that, due to the enhancement of plasma resonance on the surface of nanostructures, not only the extension of the harmonic cutoff can be found, but also the contribution of the harmonics from the long quantum path can be reduced. Further, with the control of PG technology, the contribution of supercontinuum is only from single harmonic emission peak, forming the platform area with the bandwidth of 140eV. By properly adding an ultrashort ultraviolet pulse, the harmonic yield can be enhanced by 2 orders of magnitude. By superposing this supercontinuum, a SAP with the full width at half maximum of 27as can be obtained. Moreover, the intensity of this SAP is 2 orders of magnitude higher than that produced from single PG scheme. The investigation is helpful to produce the high-intensity SAP and to advance the development of the attosecond science.
-
-
![]()
图 1 a—harmonic radiation mechanism under nanostructure b—laser field waveforms with td=0.0fs and td=6.0fs c~e—distribution of drive field intime and spale under polarization gate with x0=0.0a.u., x0=-100a.u.and x0=100a.u
![]()
图 2 Harmonic spectra from He atom driven by the spatial homogeneous and inhomogeneous single-color field and PG field(①—s=0;②—s=1, x0=0.0a.u.; ③—s=1, x0=-100a.u.; ④—s=1, x0=100a.u.)
-
[1] DRESCHER M, HENTSCHE M, KIENBERGER R, et al. Time-resolved atomic inner-shell spectroscopy[J]. Nature, 2002, 419(6909):803-807. DOI: 10.1038/nature01143
[2] UIBERACKER M, UPHUES T, SCHULTZE M, et al. Attosecond real-time observation of electron tunnelling in atoms[J]. Nature, 2007, 446(7136):627-632. DOI: 10.1038/nature05648
[3] FENG L Q, LIU H, LIU H. Spatial distribution of harmonic spectra from H2+ in the presence of spatial homogeneous and inhomogeneous field[J]. Laser Technology, 2017, 41(4):467-472(in Chinese).
[4] LIU H, FENG L Q. Mid-infrared field phase measurement and attosecond pulse generation[J]. Laser Technology, 2017, 41(2):151-158(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jgjs201702001
[5] LIU H, LI Y, YAO Z, FENG L Q. Chirp pulse control on harmonic cutoff and harmonic intensity[J]. Laser Technology, 2017, 41(5):708-711(in Chinese).
[6] ZENG Z, CHENG Y, SONG X, et al. Generation of an extreme ultraviolet supercontinuum in a two-color laser field[J]. Physical Review Letters, 2007, 98(20):203901. DOI: 10.1103/PhysRevLett.98.203901
[7] CORKUM P B. Plasma perspective on strong field multiphoton ionization[J]. Physical Review Letters, 1993, 71(13):1994-1997. DOI: 10.1103/PhysRevLett.71.1994
[8] MAIRESSE Y, BOHAN A D, FRASINSKI L J, et al. Attosecond synchronization of high-harmonic soft x-rays[J]. Science, 2003, 302(5650):1540-1543. DOI: 10.1126/science.1090277
[9] GOULIELMAKIS E, SCHULTZE M, HOFSTETTER M, et al. Single-cycle nonlinear optics[J]. Science, 2008, 320(5883):1614-1617. DOI: 10.1126/science.1157846
[10] FENG L Q, CHU T S. Generation of an isolated sub-40as pulse using two-color laser pulses:Combined chirp effects[J]. Physical Review, 2011, A84(5):053853. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=VIRT05000010000012000183000001&idtype=cvips&gifs=Yes
[11] FENG L Q, CHU T S. High-order harmonics extension and isolated attosecond pulse generation in three-color field:Controlling factors[J]. Physical Letters, 2011, A375(41):3641-3648. http://www.sciencedirect.com/science/article/pii/S0375960111010280
[12] SANSONE G, BENEDETTI E, CALEGARI F, et al. Isolated single-cycle attosecond pulses[J]. Science, 2006, 314(5798):443-446. DOI: 10.1126/science.1132838
[13] DU H C, HU B T. Broadband supercontinuum generation method combining mid-infrared chirped-pulse modulation and generalized polarization gating[J]. Optics Express, 2010, 18(25):25958-25966. DOI: 10.1364/OE.18.025958
[14] ZHANG Q B, LU P X, LAN P F, et al. Multi-cycle laser-driven broadband supercontinuum with a modulated polarization gating[J]. Optics Express, 2008, 16(13):9795-9803. DOI: 10.1364/OE.16.009795
[15] FENG L Q. Improved polarization gating scheme on attosecond source generation[J]. Spectroscopy Letters, 2016, 49(5):367-374. DOI: 10.1080/00387010.2016.1168452
[16] ZHAO K, ZHANG Q, CHINI M, et al. Tailoring a 67 attosecond pulse through advantageous phase mismatch[J]. Optics Letters, 2012, 37(18):3891-3893. DOI: 10.1364/OL.37.003891
[17] KIM S, JIN J, KIM Y J, et al. High-harmonic generation by resonant plasmon field enhancement[J]. Nature, 2008, 453(7196):757-760. DOI: 10.1038/nature07012
[18] YAVUZ I. Gas population effects in harmonic emission by plasmonic fields[J]. Physical Review, 2013, A87(5):053815. http://adsabs.harvard.edu/abs/2013PhRvA..87e3815Y
[19] FENG L Q. Molecular harmonic extension and enhancement from H2+ ions in the presence of spatially inhomogeneous fields[J]. Physical Review, 2015, A92(5):053832. DOI: 10.1103/PhysRevA.92.053832
[20] CAO X, JIANG S C, YU C, et al. Generation of isolated sub-10 attosecond pulses in spatially inhomogenous two-color fields[J]. Optics Express, 2014, 22(21):26153-26161. DOI: 10.1364/OE.22.026153
[21] LU R F, ZHANG P Y, HAN K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields[J]. Physical Review, 2008, E77(6):066701. DOI: 10.1103-PhysRevE.77.066701/
[22] HU J, HAN K L, HE G Z. Correlation quantum dynamics between an electron and D2+ molecule with attosecond resolution[J]. Physical Review Letters, 2005, 95(12):123001. DOI: 10.1103/PhysRevLett.95.123001
[23] XUE S, DU H C, XIA Y, et al. Generation of isolated attosecond pulses in bowtie-shaped nanostructure with three-color spatially inhomogeneous fields[J]. Chinese Physics, 2015, B24(5):054210. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGWL201505049.htm
[24] ANTOINE P, PIRAUX B, MAQUET A. Time profile of harmonics generated by a single atom in a strong electromagnetic field[J]. Physical Review, 1995, A51(3):R1750-R1753. http://www.ncbi.nlm.nih.gov/pubmed/9911899
[25] FENG L Q, CHU T S. Intensity enhancement in attosecond pulse generation[J]. IEEE Journal of Quantum Electronics, 2012, 48(11):1462-1466. DOI: 10.1109/JQE.2012.2207948
下载:
计量
- 文章访问数: 4
- HTML全文浏览量: 0
- PDF下载量: 6