Amplification characteristics of multiwavelength erbium-doped fiber laser amplifiers
-
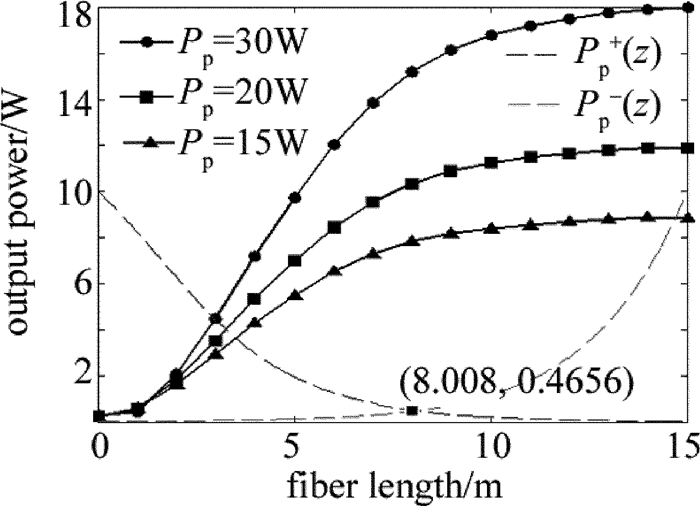
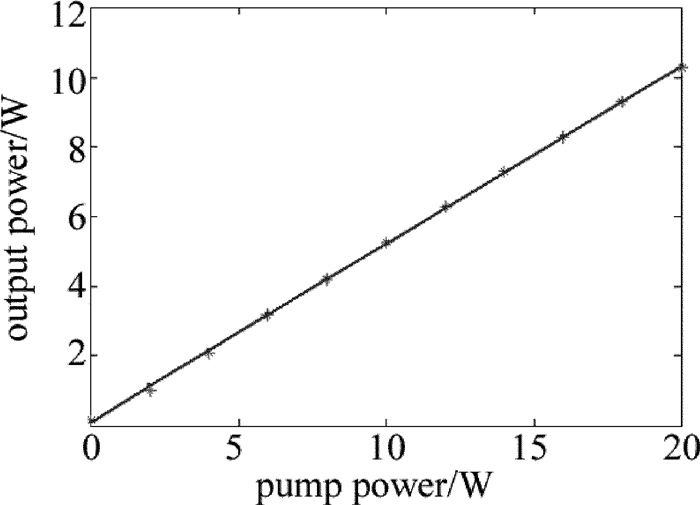
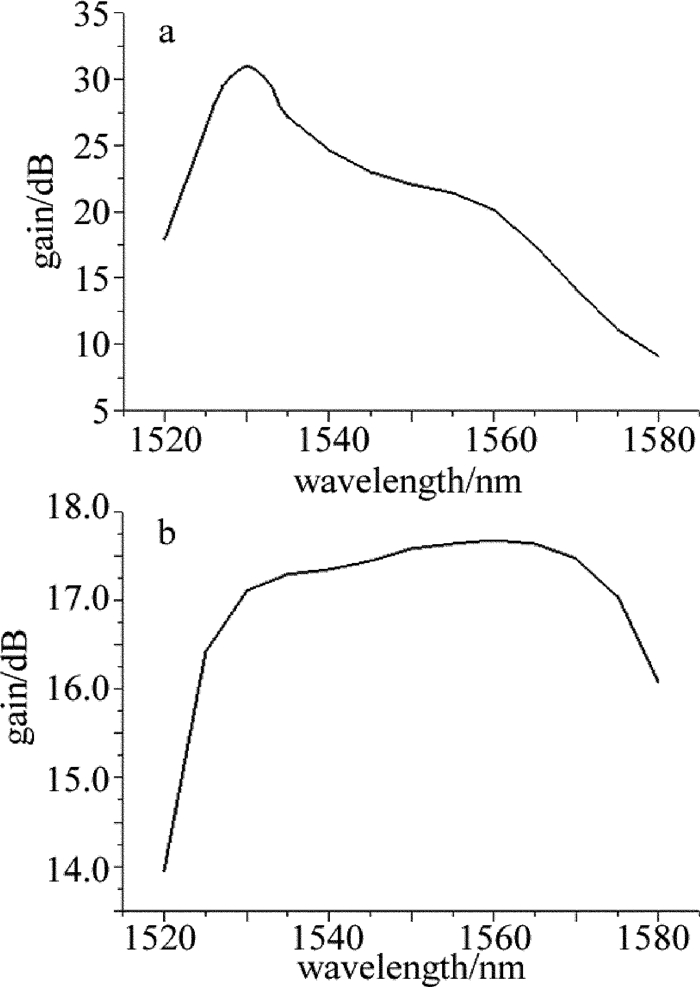
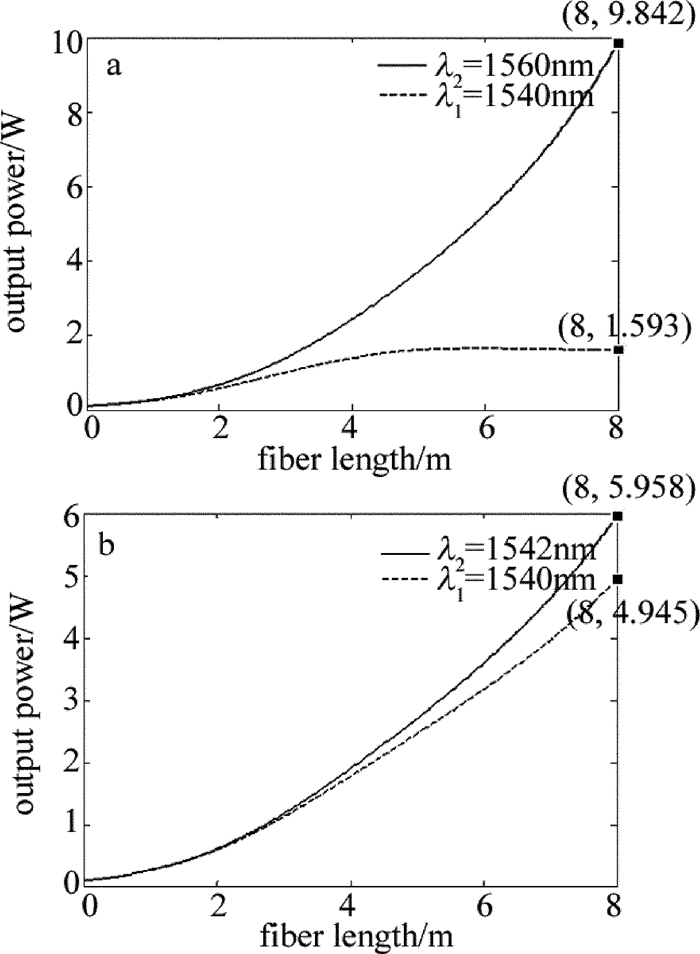
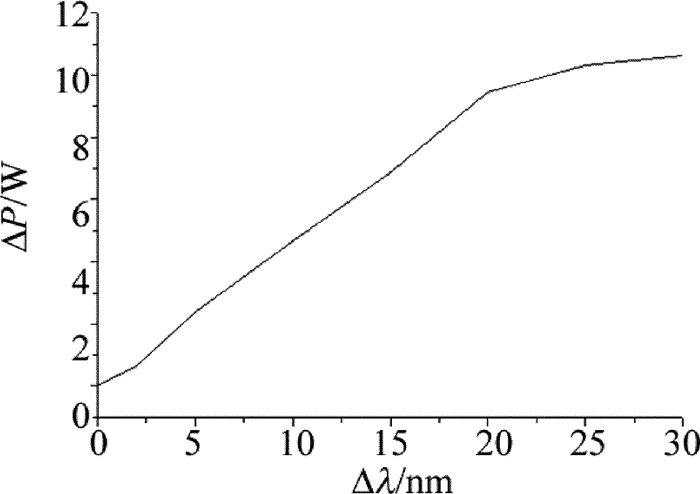
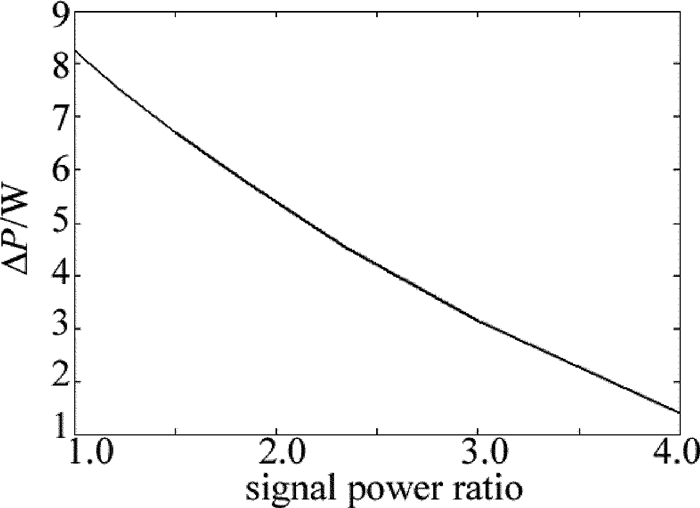
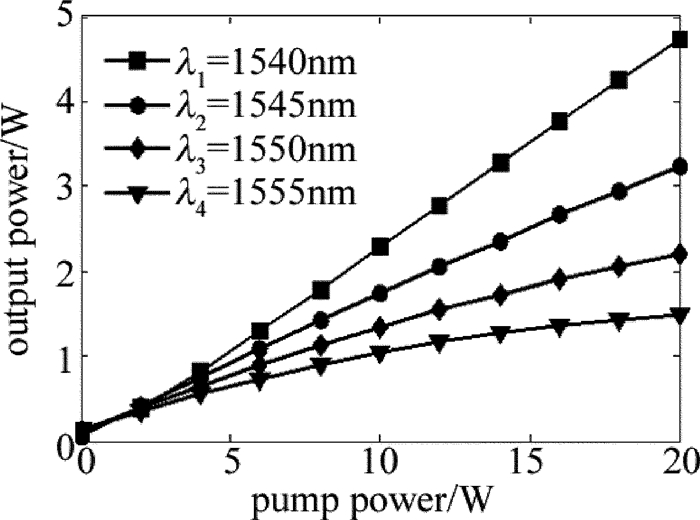
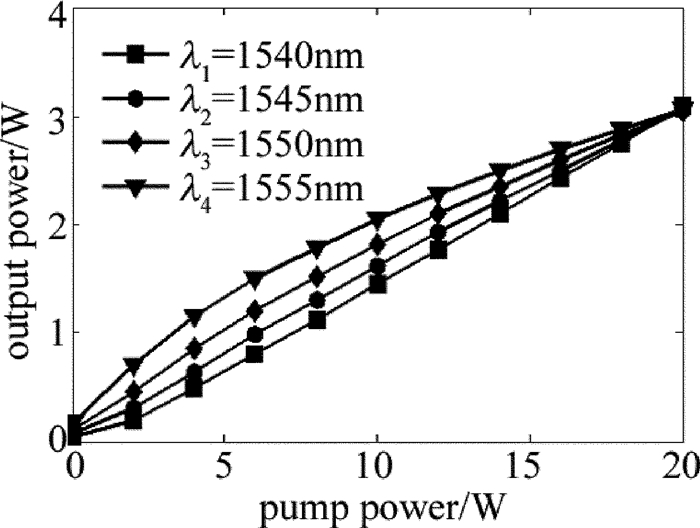
摘要: 为了研究多波长掺铒光纤激光放大器的放大特性，在单频放大器的基础上，忽略放大自发辐射，推导了描述多波长掺铒双包层光纤放大器的稳态速率方程组，建立了多波长掺铒光纤放大器的理论模型。利用该模型对单波长放大、双波长放大、四波长放大的特性，进行了数值模拟和理论分析；以四波长的激光信号放大为例，对多波长掺铒光纤放大器的放大特性，均衡增益特性进行了研究。结果表明，在单波长注入情况下，光纤放大器的掺杂光纤存在最佳光纤长度为8m；与小信号放大不同，大功率掺铒光纤放大器在1530nm~1560nm之间增益谱趋于平坦；双波长放大输出功率差随着波长间隔的增加线性增大波长间隔为20nm时，通过调节输入信号功率比可以实现最大功率差6.855W的功率均衡补偿；四波长放大时，通过信号功率配比之后的四波长激光输出功率最大偏差为0.28W，在一定范围内实现了均衡增益。这一结果对于掺铒光纤激光的多波长激光输出以及在激光多普勒测风雷达中的应用具有一定帮助。
-
关键词:
- 光纤放大器 /
- 多波长掺铒光纤放大器 /
- 功率均衡调制 /
- 波长间隔 /
- 增益谱
Abstract: In order to study amplification characteristics of a multi-wavelength erbium-doped fiber amplifier (EDFA), steady rate equation for a multi-wavelength Er-doped double cladding fiber amplifier was deduced based on a single frequency amplifier and ignoring the amplified spontaneous emission (ASE). A theoretical model of EDFA was set up. The amplification characteristics of single wavelength amplification, dual wavelength amplification and four-wavelength amplification were numerically simulated and analyzed theoretically by using this model. The results indicate that, the optimum fiber length of the doped fiber amplifier is 8m in case of single wavelength injection. Unlike small signal amplification, the gain spectrum of a high-power EDFA tends to be flat in the range of 1530nm~1560nm. The difference of output power increases linearly with the increase of wavelength interval when double-wavelength signal laser is amplified by EDFA. While wavelength interval is 20nm, the maximum power difference of power balance compensation is 6.855W by adjusting the input signal power ratio. The minimum deviation of output power is 0.28W by adjusting the wavelength interval and power ratio parameter when four-wavelength signal laser is amplified by EDFA. And the gain equalization can be easily achieved within a certain range. The study will be helpful for multi-wavelength Er-doped fiber lasers and their application in laser Doppler radars. -
-
![]()
Figure 5. Gain spectra of EDFA under different input conditions
a—Pp=150mW, Ps=1μW b—Pp=20W, Ps=100mW
![]()
Figure 6. Signal distribution along the fiber of dual-wavelength amplification
a—Δλ=20nm(λ1=1540nm, λ2=1560nm) b—Δλ=2nm(λ1=1540nm, λ2=1542nm)
![]()
Figure 9. Four wavelength amplification characteristics with the same input signal power
![]()
Figure 10. Four wavelength amplification characteristics with different input signal powers
Table 1 Physical parameters for theoretical calculations of amplifiers[19]
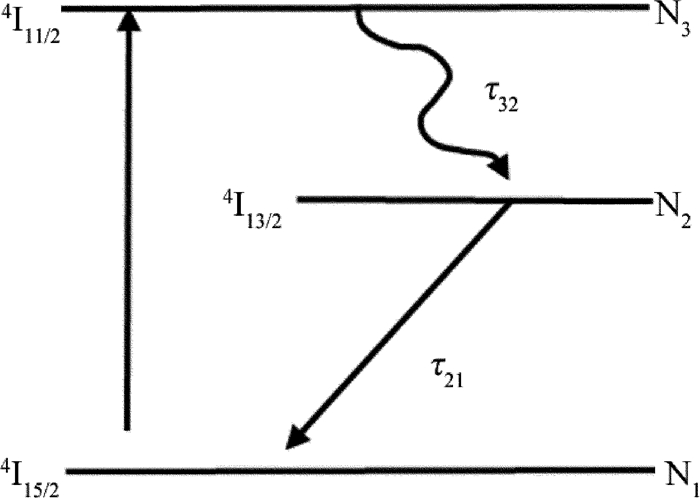
symbol definition value N erbium concentration 1.0×1025m-3 τ upper-level particle lifetime 10.8×10-3s δe, p(λi) pump emission cross-section 1.75×10-25m2 δe, s(λi) signal emission cross-section 6.5×10-25m2 δa, s signal aborsoption cross-section 7×10-25m2 A fiber core area 5.8×10-10m2 αs signal fiberattenuation coefficient 2×10-3m-1 αp pump fiber attenuation coefficient 4×10-4m-1 Γp pump filling factor 0.811 Γs signal filling factor 0.6 
下载: 导出CSV
-
[1] MARAN J, LAROCHELLE S, BESNARD P, et al.C-band multi-wavelength frequency-shifted erbium doped fiber laser[J].Optics Communications, 2003, 218(1):81-86. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ024966575/
[2] BELLEMARE A, KARASEK M, ROCHETTE M, et al. Room temperature multi-frequency erbium-doped fiber lasers anchored on the ITU frequency gdd[J].Journal of Lightwave Technology, 2000, 18(6):825-831. DOI: 10.1109/50.848393
[3] KIM S K, CHU M J, LEE J H, et al. Wideband multi-wavelength erbium-doped fiber ring laser with frequency shifted feedback[J].Optics Communications, 2001, 190(1):291-302. http://www.sciencedirect.com/science/article/pii/S0030401801010732
[4] WANG R, WENG D, LI K, et al.Multi-wavelength Erbium-doped fiber laser based on four wave mixing effect in single mode fiber and high nonlinear fiber[J].Optics Express, 2013, 21(10):12570-12578. DOI: 10.1364/OE.21.012570
[5] XIAO P P, DENG M L, HU H W. Multi-wavelength and single longitudinal mode brillouinfiber lasers based on passive cavities[J].Laser Technology, 2016, 40(5):727-729(in Chinese). http://www.jgjs.net.cn/EN/Y2016/V40/I5/727
[6] SHAHABUDDIN N S, AHMAD H, YUSOFF Z, et al. Spacing-switchable multi-wavelength fiber laser based on nonlinear polarization rotation and brillouinscatteringin photonic crystal fiber[J].IEEE Photonics Journal, 2012, 4(1):34-38. DOI: 10.1109/JPHOT.2011.2178400
[7] YAO B, TONG Zh R, YANG X F, et al .Tunable multiwavelength fiber laser based on stimulated brillouin scattering[J]. Infrared and Laser Engineering, 2012, 41(4):919-923(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-HWYJ201204016.htm
[8] WANG R G, ZHAO L, ZHANG X P. Research of tunable multi-wavelength laser based on amplification effect of stimulated brillouin scattering[J].Journal of Optoelectronics·Laser, 2015, 26(6):1025-1029(in Chinese).
[9] LI Y, FENG X H, SUN L, et al. Dual-wavelength fiber laser based on polarization hole-burning effect at room temperature[J].Acta Photonica Sinica, 2005, 34(2):173-175(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-GZXB200502003.htm
[10] DONG F J, YANG X F, CAO Y, et al. Dual-wavelength Er-doped fiber laser based on polarization hole burning of multi-mode fiber[J].Journal of Optoelectronics·Laser, 2011, 22(6):841-844(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GDZJ201106009.htm
[11] ZHANG Ch F, SUN J, JIAN Sh Sh, et al. A new mechanism to suppress the homogeneous gain broadening for stable multi-wavelength erbium-doped fiber laser[J].Optics Communications, 2013, 288(2):97-100. http://www.sciencedirect.com/science/article/pii/S0030401812010863
[12] DONG J L, SUN J Q.Multiwavelength erbium-doped fiber laser based on frequency shift and polarization hole burning[J].Laser Technology, 2008, 32(2):210-214(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs200802020
[13] HE X K, HOU H, FENG L T, et al. Experimental study of 1550nm single frequency pulsed fiber laser amplifier[J]. Laser Technology, 2011, 35(2):146-151(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS201102002.htm
[14] ZHANG X, LIU Y, HE Y, et al.Characteristics of eye-safe high repetition frequency narrow pulse width single mode all fiber laser[J].Infrared and Laser Engineering, 2015, 44(4):1105-1109(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hwyjggc201504001
[15] SHINIZU M, HORIGUCHI M, YAMADA M, et al.Highly efficient integrated optical fiber amplifier module pumped by a 0.98nm laser diode[J].Electronics Letters, 1990, 26(8):498-501. DOI: 10.1049/el:19900324
[16] DU G G, CHEN G F, LIU D F. Theoretical Studies on the distribution of pump power for 980nm pumped erbium-doped fiber amplifier[J].Acta Photonica Sinica, 2000, 20(2):175-180(in Chinese). http://en.cnki.com.cn/article_en/cjfdtotal-gxxb200002004.htm
[17] ZHAO Zh Y. Theoretical and experimental study on high power photonics crystal fiber amplifier[D].Xi'an: Xi'an Institute of Optics and Precision Mechanics, Chinese Academy of Science, 2009: 18-22(in Chinese).
[18] LENG J Y. Theoretical and experimental study of narrow linewidth fiber amplifier[D]. Changsha: National University of Defense Technology, 2011: 59-62(in Chinese).
[19] XU H B, CHEN L. Studies on the out put characteristic of erbium-doped fiber laser[J].Acta Photonica Sinica, 2004, 33(7):777-781(in Chinese).
[20] ZHOU Y X, NIE Q H, ZHOU Y, et al. Numerical Simulations on gain saturation characteristics of erbium-doped tellurite-based optical fiber amplifier.[J]Acta Photonica Sinica, 2003, 32(6):679-682(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GZXB200306010.htm
[21] JIANG Ch, ZHOU Y X, NIE Q H, et al.Numerical simulations on gain equalization of erbium-doped tellurite-based optical fiber amplifier[J]. Chinese Journal of Quantum Electronics, 2006, 23(4):542-545(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lzdzxb200604021
计量
- 文章访问数: 5
- HTML全文浏览量: 1
- PDF下载量: 7