网站地图
下载:
-
随着偏光技术以及激光应用的快速发展，各种偏光分束器件得到了越来越广泛的应用，其中Wollaston棱镜是最典型的也是目前应用和研究较广泛的偏光分束棱镜[1-4]。由于Wollaston棱镜被分束的o光、e光均发生偏折，具有较大的分束角[5-7]，因此在航空、医疗以及环境监测等领域都有着重要应用[8-12]。传统Wollaston棱镜由光轴相互正交的冰洲石晶体组成。研究表明，传统Wollaston棱镜分束角并不具有完全的对称性，且随着结构角的增大，分束角的不对称性越来越明显[13-15]。但在某些特殊的偏光技术应用中，要求分束角严格对称[16]，这是传统Wollaston棱镜所不能满足的。ZHANG等人提出了一种修正式Wollaston对称分束棱镜[17]，此棱镜不仅结构简单，而且可以实现对称分束。本文中针对这种对称分束棱镜，讨论了其出射的o光、e光分束角与棱镜结构角和修正角的关系、光强分束比随结构角的变化以及入射角变化对棱镜分束角和出射光对称性的影响，为该棱镜的设计和应用提供了理论指导。
-
Wollaston式对称分束棱镜结构以及分光光路图如图 1所示。图中，1、2、3分别表示光线经过棱镜时的3个界面，S为棱镜的结构角；双箭头以及圆点表示晶轴的方向；θ1和θ2分别为第2块方解石晶体中o光和e光与水平方向的夹角；φ1和φ2分别是o光和e光与水平方向的夹角。为了实现对称分束，在传统Wo-llaston棱镜结构的基础上，对棱镜的出射端面3进行角度为Δφ的修正，使得φ1=φ2。这里，把Δφ称为修正角，φ1和φ2分别称为o光分束角和e光分束角。这种设计既保证了棱镜的对称分束，同时也保证了棱镜有较大的分束角。
Figure 1. Schematic of optical path of Wollaston-type symmetric beam-splitting prism
-
如图 1所示，由于入射光垂直入射到界面1，光轴和入射光垂直，因此o光、e光将以不同的相速度沿入射光方向同向传播。其中，o光和e光分别垂直于主截面(纸面)和平行于主截面振动。光线进入第2块晶体时，由于光轴方向垂直于纸面，因此在通过界面2后，第1块晶体中的o光、e光将分别变为e光、o光。最后，在界面3处，o光、e光分别以φ1+Δφ和φ2-Δφ的折射角出射。
根据折射定律，在修正面3处有：
$ \left\{ \begin{array}{l} {\varphi _1} = \arcsin \left[ {{n_{\rm{o}}}\sin \left( {{\theta _1} + \Delta \varphi } \right)} \right] - \Delta \varphi \\ {\varphi _2} = \arcsin \left[ {{n_{\rm{e}}}\sin \left( {{\theta _2} - \Delta \varphi } \right)} \right] + \Delta \varphi \end{array} \right. $
(1) 其中：
$ \left\{ \begin{array}{l} {\theta _1} = S - \arcsin \left( {\frac{{{n_{\rm{e}}}}}{{{n_{\rm{o}}}}}\sin S} \right)\\ {\theta _2} = \arcsin \left( {\frac{{{n_{\rm{o}}}}}{{{n_{\rm{e}}}}}\sin S} \right) - S \end{array} \right. $
(2) 式中，no, ne分别为o光和e光在晶体中的主折射率。作者选取入射光波长λ=632.8nm，no=1.658，ne=1.486。将(2)式分别带入(1)式可得到o光、e光分束角关于结构角S和修正角Δφ的关系，如图 2所示。
Figure 2. Relationship among splitting angle of o light and e light, structure angle and deviation angle
由图 2可知，当修正角Δφ=0时为传统Wollaston棱镜，此时φ2和φ1随棱镜结构角的增大而增大，且总有φ2>φ1。在棱镜结构角大于20°以后，φ1和φ2的差值逐渐变大，棱镜的对称分束性能也越来越差。图 2中两曲面重合曲线表示当实现对称分束，即φ1=φ2时，修正角随结构角的变化关系，可见当实现对称分束时，随着棱镜结构角增大，修正角也要增大。通常情况下一般选取Wollaston棱镜的结构角在20°~40°之间，相应的修正角在0.05°~0.97°之间变化。
-
由图 1可知，出射的o光和e光分别经过了界面1、界面2和界面3，把第1块棱镜中的o光称为第1束光，第1块棱镜中的e光称为第2束光。
其中第1束光振动方向垂直于入射面为s振动，根据菲涅耳公式，其在各界面的强度反射系数为：
$ {R_{s,1}} = {\left( {\frac{{n - {n_{\rm{o}}}}}{{n + {n_{\rm{o}}}}}} \right)^2} $
(3) $ {R_{s,i}} = \frac{{{{\sin }^2}\left( {{A_i} - {B_i}} \right)}}{{{{\sin }^2}\left( {{A_i} + {B_i}} \right)}} $
(4) 式中，当i=2时, 第1束光在第2个界面对应的折射角和反射角分别为A2=θs,2,B2=S; 当i=3时，第1束光在第3个界面对应的折射角和反射角分别为A3=φ2-Δφ, B3=θ2-Δφ; θs,2和n分别为第1束光在界面2处的折射角和空气折射率。
设入射自然光光强I，Wollaston式对称分束棱镜的e光透射光强为：
$ {I_{\rm{e}}} = \frac{I}{2}\left( {1 - {R_{s,1}}} \right)\left( {1 - {R_{s,2}}} \right)\left( {1 - {R_{s,3}}} \right) $
(5) 对于第2束光其振动方向在入射面内为p振动，同理可得：
$ {I_{\rm{o}}} = \frac{I}{2}\left( {1 - {R_{p,1}}} \right)\left( {1 - {R_{p,2}}} \right)\left( {1 - {R_{p,3}}} \right) $
(6) $ {R_{p,1}} = {\left( {\frac{{{n_{\rm{e}}} - n}}{{n + {n_{\rm{e}}}}}} \right)^2} $
(7) $ {R_{p,i}} = \frac{{{{\tan }^2}\left( {{C_i} - {D_i}} \right)}}{{{{\tan }^2}\left( {{C_i} + {D_i}} \right)}} $
(8) 式中，当i=2时，第2束光在第2个界面对应的反射角和折射角分别为C2=S, D2=θp,2; 当i=3时，第2束光在第3个界面对应的反射角和折射角分别为C3=θ1+Δφ, D3=φ1+Δφ; θp,2为第2束光通过界面2的折射角。
结合折射公式可得e光、o光的光强分束比F=Ie/Io，F随结构角变化的曲线如图 3所示。由图可见：在实现对称分束时，棱镜的光强分束比在0.98以上，且分束比随结构角的变化幅度不明显。
图 3 Relationship between intensity radio and structure angle
-
图 4中S是棱镜结构角，α, β分别为光线在界面1处的入射角和o光折射角，i2, γ为o光在界面2处的入射角和折射角，i3, φ2－Δφ为e光在出射端面3处的入射角和折射角。当第1束光线入射到棱镜后，在界面1、界面2、界面3处，利用折射定律可得到下列关系式：
$ \left\{ \begin{array}{l} n\sin \alpha = {n_{\rm{o}}}\sin \beta \\ {i_2} = S + \beta \\ {i_3} = \gamma - S - \Delta \varphi \\ {n_{\rm{o}}}\sin {i_2} = {n_{\rm{e}}}\sin \gamma \\ {n_{\rm{e}}}\sin {i_3} = n\sin \left( {{\varphi _2} - \Delta \varphi } \right) \end{array} \right. $
(9) 
Figure 4. Optical path of the first light beam under non-vertical incidence
联立(9)式，可得到第1束光即出射光e光分束角φ2与结构角S和入射角α的关系。
-
如图 5所示建立空间坐标系，以第1块晶体的光轴方向为y轴正方向，以第2块晶体光轴方向为x轴正方向，z轴沿水平方向。其中α为光线入射角；ek, es分别代表e光波波矢方向单位矢量和e光线方向单位矢量；θk为e光波波矢方向与界面1法线的夹角；θk,s为离散角，即e光波波矢ek和e光线es的夹角；θ2,e, θ2,o分别为e光波在界面2处的入射角和折射角；θ3,o, φ1+Δφ分别为o光在出射端面3处的入射角和折射角。
Figure 5. Optical path of the second light beam under non-vertical incidence
由于第1块晶体中的主截面和入射面重合，此时e光波和e光线都在主截面内[18]。方解石为负单轴晶体，因此e光线较其波法线远离光轴[19-20]。若$ {\mathit{\boldsymbol{\hat e}}_x}, {\mathit{\boldsymbol{\hat e}}_y}, {\mathit{\boldsymbol{\hat e}}_z}$分别代表x, y, z方向的单位矢量，则光轴方向可表示为:
$ {\mathit{\boldsymbol{e}}_p} = {{\mathit{\boldsymbol{\hat e}}}_y} $
(10) e光波矢可表示为：
$ {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{k}}} = - \sin {\theta _\mathit{\boldsymbol{k}}}{{\mathit{\boldsymbol{\hat e}}}_y} + \cos {\theta _\mathit{\boldsymbol{k}}}{{\mathit{\boldsymbol{\hat e}}}_z} $
(11) 对于e光，其折射率大小与波矢量和光轴夹角θk,p有关，即:
$ {n_{\rm{e}}}^\prime = \frac{{{n_{\rm{o}}}{n_{\rm{e}}}}}{{\sqrt {n_{\rm{o}}^2{{\sin }^2}{\theta _{\mathit{\boldsymbol{k}},p}} + n_{\rm{e}}^2{{\cos }^2}{\theta _{\mathit{\boldsymbol{k}},p}}} }} $
(12) 在界面1处根据折射定律有：
$ n\sin \alpha = \frac{{{n_{\rm{o}}}{n_{\rm{e}}}}}{{\sqrt {n_{\rm{o}}^2{{\sin }^2}{\theta _{\mathit{\boldsymbol{k}},p}} + n_{\rm{e}}^2{{\cos }^2}{\theta _{\mathit{\boldsymbol{k}},p}}} }}\sin {\theta _\mathit{\boldsymbol{k}}} $
(13) 联立(10)式、(11)式可得:
$ \cos {\theta _{\mathit{\boldsymbol{k}},p}} = {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{k}}} \cdot {\mathit{\boldsymbol{e}}_p} = - \sin {\theta _\mathit{\boldsymbol{k}}} $
(14) 将(14)式代入(13)式中，可得：
$ \tan {\theta _\mathit{\boldsymbol{k}}} = \frac{{{n_{\rm{o}}} \cdot n\sin \alpha }}{{{n_{\rm{e}}}\sqrt {n_{\rm{o}}^2 - {n^2}{{\sin }^2}\alpha } }} $
(15) 由图 5可知，e光波在界面2处和界面3处的入射角分别为θ2,e=θk+S和θ3,o=S－θ2,o+Δφ，在界面2和界面3处，由折射定律可得：
$ {{n'}_{\rm{e}}}\sin {\theta _{2,{\rm{e}}}} = {n_{\rm{o}}}\sin {\theta _{2,{\rm{o}}}} $
(16) $ {n_{\rm{o}}}\sin {\theta _{3,{\rm{o}}}} = n\sin \left( {{\varphi _1} + \Delta \varphi } \right) $
(17) 结合(14)式~(17)式，可得o光分束角φ1与结构角S和入射角α的关系。
-
定义m=|φ1－φ2|为出射光束的不对称度，φ=φ1+φ2为棱镜分束角，则m越大表示棱镜对称分束性能越差，φ越大表示棱镜分束性能越好。结合(12)式~(17)式，可得棱镜分束角φ、出射光线不对称度m随结构角S和入射角α的变化关系，如图 6所示。
Figure 6. a—relationship among splitting angle, structure angle and incident angle b—relationship among asymmetry degree, structure angle and incident angle
由图 6可知：修正式Wollaston棱镜分束角随棱镜结构角的增大而增大，但随入射角的变化不明显。当棱镜结构角S=30°，光线入射角从-3°~+3°变化时，棱镜分束角变化约为0.01°，可见入射角的轻微变动对分束角的影响可以忽略；相反，棱镜两出射光线的不对称度m受入射角变化影响较大，但随结构角的变化很小。可以看出，光线分别以正角度和负角度入射时，不对称度的变化近似关于入射角为零时对称，当入射角在-3°~+3°之间变化时，两出射光线的不对称度小于6°。
-
基于折射定律和菲涅耳公式，对一种修正式Wollaston对称分束棱镜的分束特性进行了研究。理论分析表明：棱镜出射的o光、e光与水平方向夹角主要取决于棱镜结构角，受棱镜修正角影响较小；当棱镜结构角在20°~45°之间时，相应的修正角在0.05°~0.97°之间变化，棱镜的光强分束比保持在0.98以上，且分束比随结构角的变化幅度很小；以小角度入射时，入射角主要影响出射光束对称性，当入射角在-3°~3°之间变化时，两出射光线的不对称度小于6°，可以保证较好的对称分束效果。
一种Wollaston式偏光棱镜分束特性的研究
Analysis of beam-splitting characteristics of Wollaston-type polarizing prisms
-
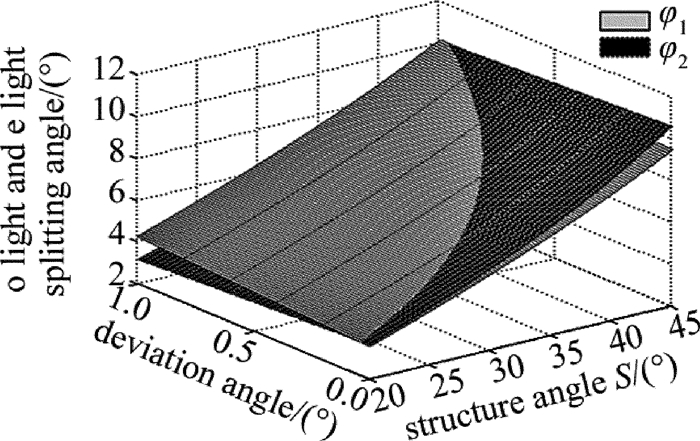
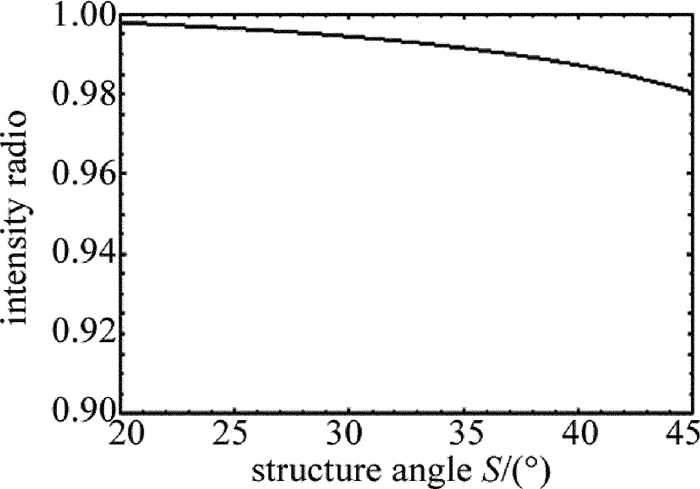
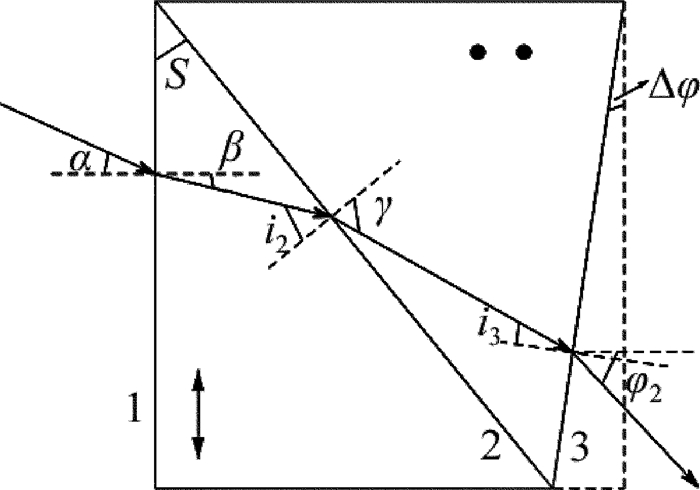
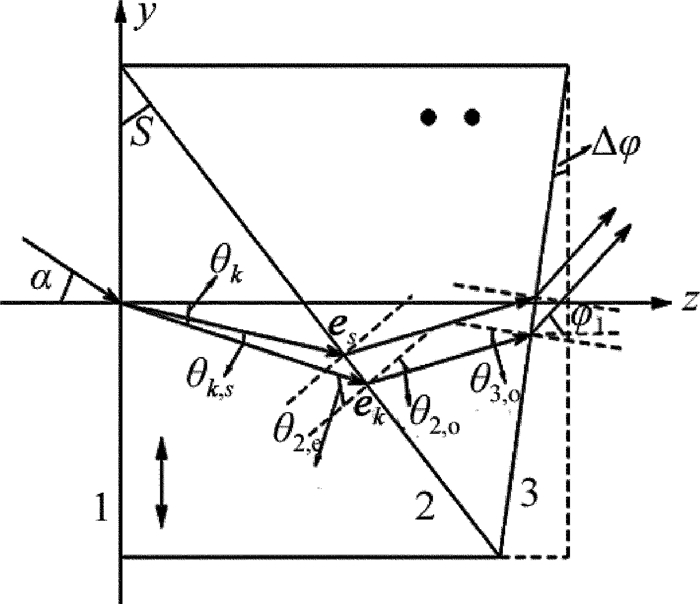
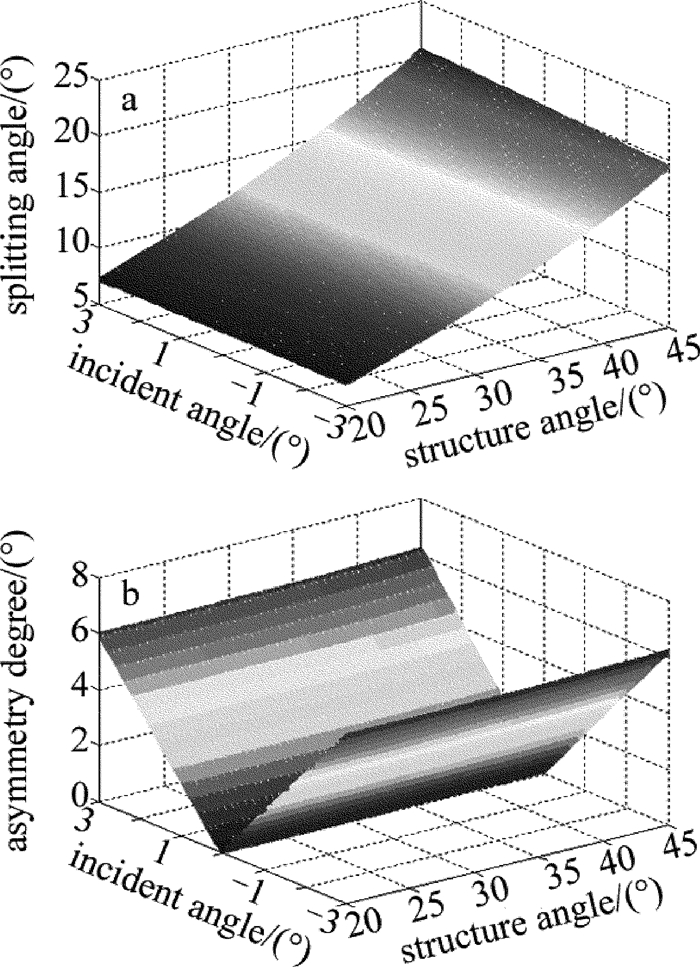
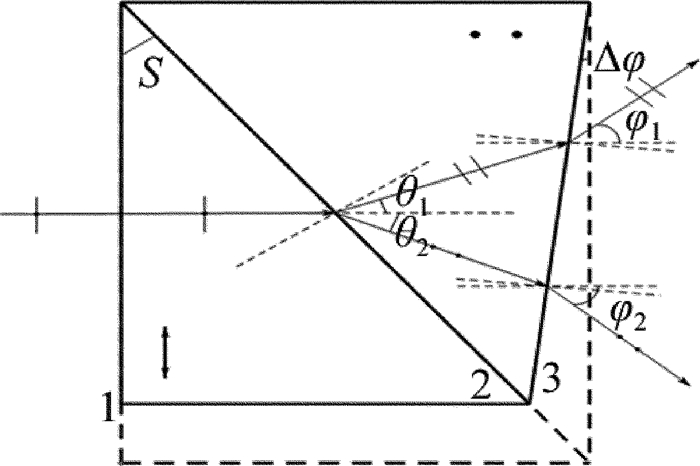
摘要: 为了对一种修正式对称分束Wollaston棱镜的分束特性进行系统分析，利用折射定律和菲涅耳公式，以632.8nm波长为例，给出了出射光与水平方向的夹角随修正角、结构角之间的变化关系曲线、光强分束比随结构角的变化关系以及入射角对棱镜分束角和出射光束对称性的影响曲线。结果表明，通过对出射端面的修正可以实现Wollaston棱镜的严格对称分束；o光、e光分束角主要取决于棱镜结构角，受棱镜修正角影响较小；光强分束比随结构角的增大变化幅度较小；当光线以小角度入射时，入射角主要影响棱镜分束角对称性；入射角在-3°~3°之间变化时，两出射光线的不对称度小于6°，可以保证较好的对称分束效果。该研究为该棱镜的设计和应用提供了理论指导。Abstract: In order to analysis systematically the splitting characteristics of a Wollaston-type symmetric beam-splitting prism, by using refractive formula and Fresnel formula and taking 632.8nm for example, relationship curve among the angle of emergent light to the horizontal direction, deviation angle and structure angle, relationship curve between intensity splitting beam ratio and structure angle, relationship curve among incident angle, splitting beam angle of the prism and emerging light symmetry were gotten. The results show that, strict symmetric beam can be achieved through the correction of output face of Wollaston prism. Splitting angles of o light and e light mainly depend on the prism structure angle. The effect of deviation angle is smaller. The changing magnification of beam splitting ratio with the increase of structure angle is small. When the incident angle is small, it has main effect on the symmetry of prism splitting angle. When incident angle changes between-3ånd+3°, the asymmetry degree of two beam is less than 6°, which can guarantee good effect of symmetry beam splitting. The study provides a theoretical guidance for design and application of the prism.
-
Key words:
- optical devices /
- Wollaston prism /
- incident angle /
- structure angle /
- beam-splitting angle /
- beam-splitting radio
-
Figure 2. Relationship among splitting angle of o light and e light, structure angle and deviation angle
-
[1] YAO H T, LI G H, PENG H D, et al. The splitting angle and light intensity ratio of Wollaston prism within its viewing field angle[J]. Journal of Qufu Normal University, 2008, 34(2):51-54(in Chinese). [2] MA L L, SONG L K, WU F Q. Design of parallel and symmetric beam splitting prism based on Wollaston prism[J]. Optical Technique, 2003, 29(5):602-603(in Chinese). [3] ZHU H F, SONG L K, WANG X M. Study about splitting intensity ratio of a prism with variable beam splitting angle[J]. Optical Technique, 2003, 29(5):614-616(in Chinese). [4] ZHU H F, HAN R F, GUO W T, et al. Analysis of optical properties of Wollaston-type parallel-splitting prism[J]. Acta Photonica Sinica, 2013, 42(9):1118-1122(in Chinese). doi: 10.3788/gzxb [5] ZHAO K H, ZHONG X H. Optics(Ⅱ)[M]. Beijing:Peking University Press, 1984:182-183(in Chinese). [6] DENG H Y, WU F Q, TANG H J. The spectral properties of the splitting angle for Wollaston prism[J]. Laser Journal, 2005, 26(4):42-43(in Chinese). [7] ZHANG Ch M. Interference imaging spectroscopy[M]. Beijing:Science Press, 2010:47-49(in Chinese). [8] ZHANG Ch M, ZHAO B Ch, XIANG L B, et al. Wide-field-of-view polarization interference imaging spectrometer[J]. Applied Optics, 2004, 43(33):6090-6094. doi: 10.1364/AO.43.006090 [9] LIU J, JIN W Q, WANG Y H, et al. Design of simultaneous imaging polarimetry with double separate Wollaston prism[J]. Acta Optica Sinica, 2015, 35(5):0511001(in Chinese). doi: 10.3788/AOS [10] LIN X, ZHOU F, LI H, et al. Static Fourier-transform spectrometer based on Wollaston prism[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(14):3482-3484. doi: 10.1016/j.ijleo.2014.01.062 [11] KUDENOV M W, MISKIEWICZ M, SANDERS N, et al. Achromatic Wollaston prism beam splitter using polarization gratings[J]. Optics Letters, 2016, 41(19):4461-4463. doi: 10.1364/OL.41.004461 [12] WU H Y, ZHANG Ch M, ZHAO B Ch. Theoretial analysis on extending the field-of-view of the imaging spectrometer based on combined Wollaston prisms[J]. Acta Physica Sinica, 2009, 58(2):930-935(in Chinese). [13] HUANG J Y, WU F Q, LI G H. Symmetry of beam splitting angle for uniaxial crystal prism[J]. Laser Technology, 1996, 20(2):104-107(in Chinese). [14] HUANG J Y, WU F Q. The study about design and measure of uniaxial crystal prism with excellecent symmetry of the beam splitting angle[J]. Journal of Optoelectronics·Laser, 1995, 6(4):211-215(in Chinese). [15] LI G H, WU F Q, YU D H. Study of asymmetry of beam splitting angle for polarization beam splitting prism[J]. Journal of Applied Optics, 1991, 12(4):21-25(in Chinese). [16] MENG F H, SONG L K, KONG F Zh, et al. A new symmetric beam-splitting polarization prism[J]. Laser Technology, 2006, 30(6):670-672(in Chinese). [17] ZHANG X, WU F Q, PENG H D, et al. Symmetric beam splitting prism based on Wollaston prism[J]. Laser Journal, 2008, 29(1):21-22(in Chinese). [18] SHEN W M, SHAO Zh X. Dispersion between ordinary ray and extraordinary ray in unisxial crystals for any orientation of optical axis[J]. Acta Optica Sinica, 2002, 22(6):765-768(in Chinese). [19] WU L, ZHANG Ch M, YUAN Y, et al. Exact calculation of the lateral displacement and optical path difference of savart polariscopes[J]. Acta Optica Sinica, 2005, 25(7):886-889(in Chinese). [20] LIAO Y B. Polarization optics[M]. Beijing:Science Press, 2003:71-79(in Chinese). -
点击查看大图
图(6)
计量
- 文章访问数: 7695
- HTML全文浏览量: 5492
- PDF下载量: 282
- 被引次数: 0
