Improvement of system tunability for Fano resonance by graphene-dielectric stack
-
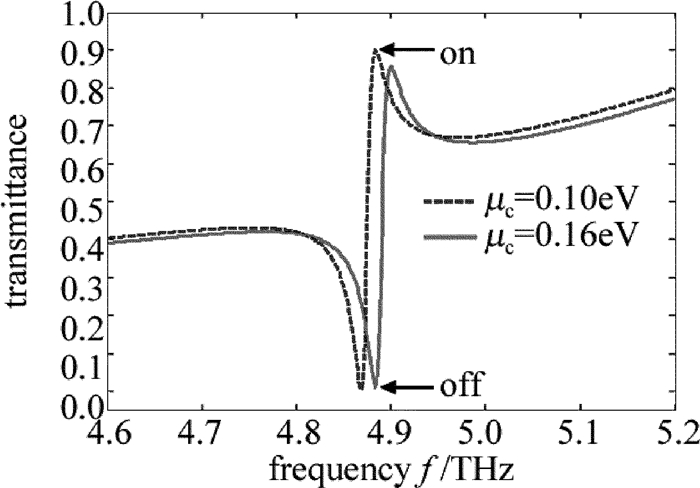
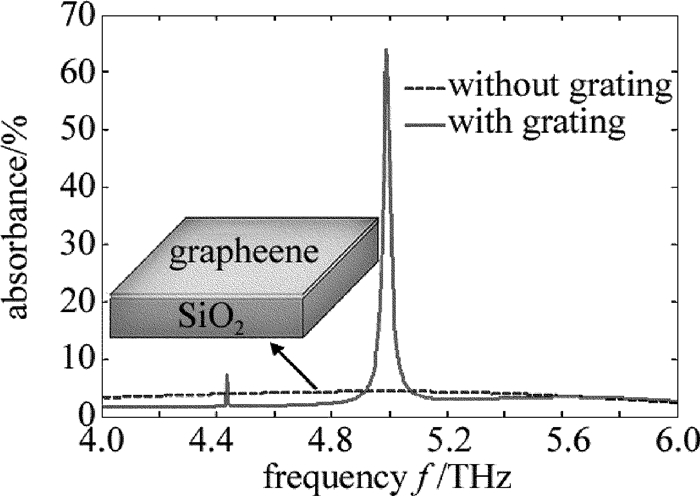
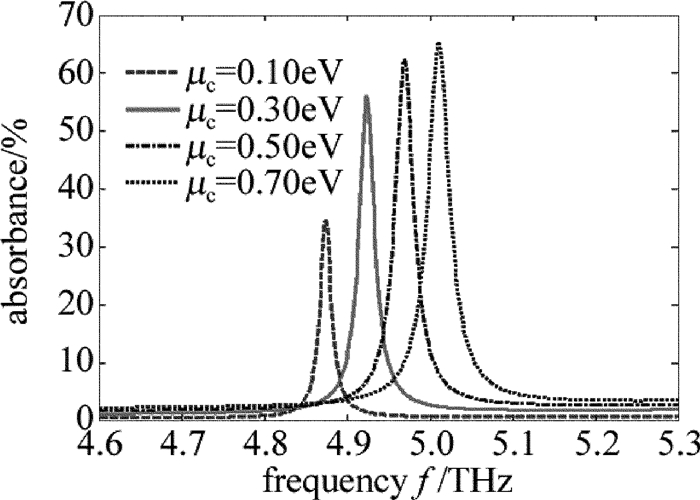
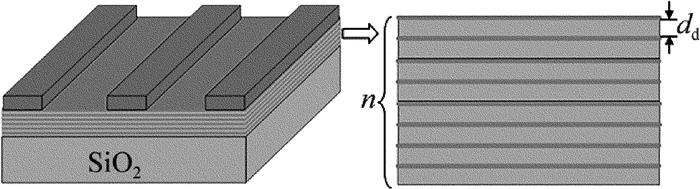
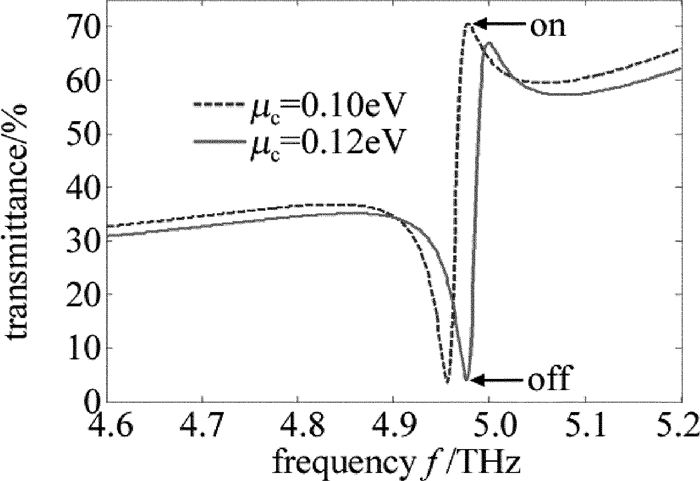
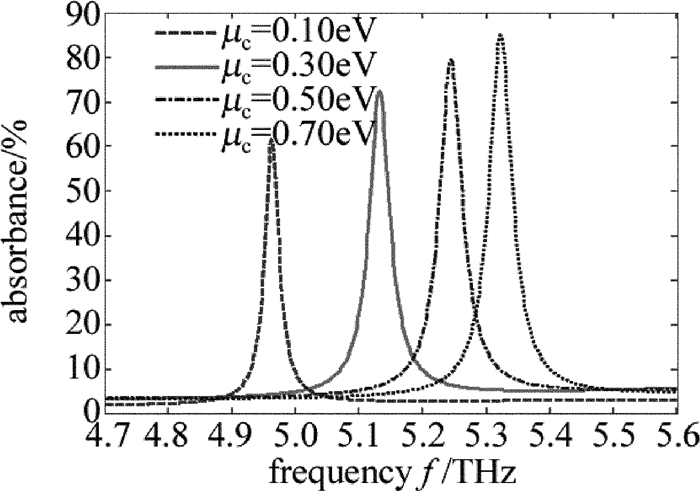
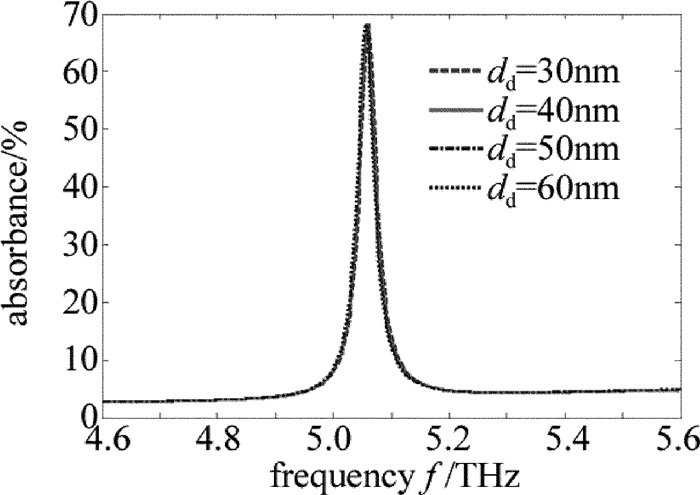
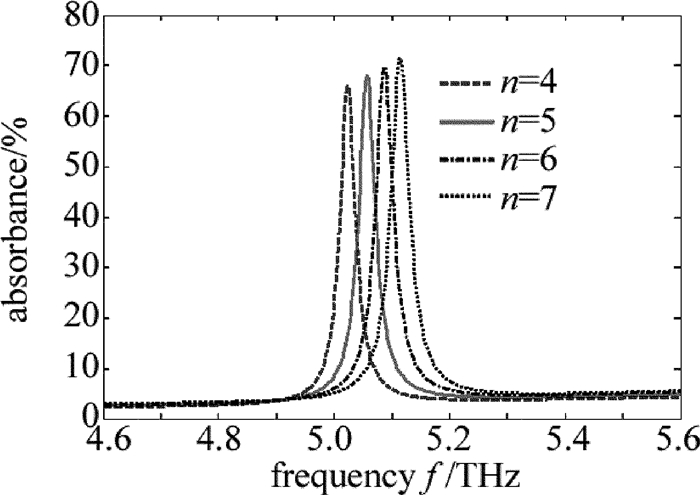
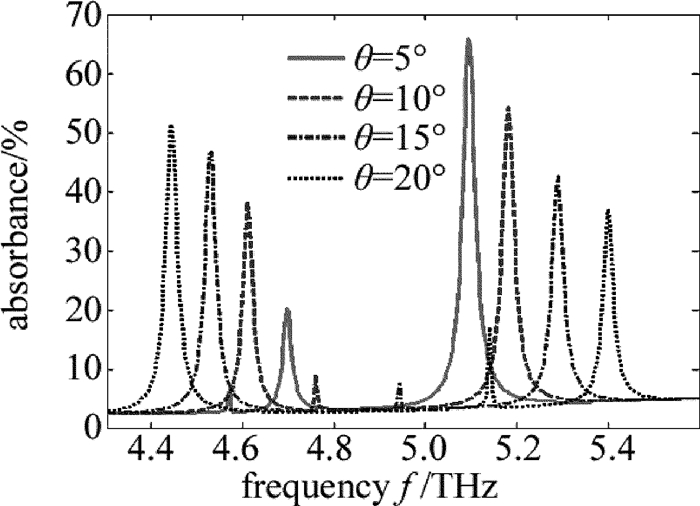
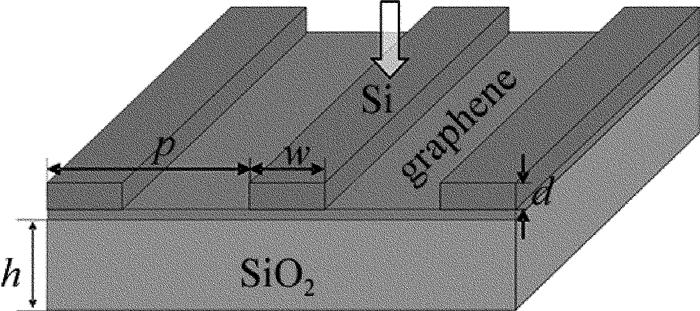
摘要: 为了更加有效地利用亚波长光栅/介质波导结构调控Fano共振，使用石墨烯介质堆栈代替石墨烯单层作为缓冲层，采用严格耦合波分析方法仿真改进后的结构，研究了堆栈单元中纳米级介质厚度增强石墨烯电导率的变化对整个堆栈结构等效介电常数的影响。结果表明，若系统作为高效光开关使用，则所需的石墨烯化学势改变由原来的0.06eV减小到了0.02eV，且开关调制深度高达94%；若系统作为可调谐吸波体使用，则其频率调制深度由原来的0.14THz增加到了0.36THz，大大扩展了吸收谱的调节范围。改进的结构提高了系统调控Fano的能力。Abstract: To enhance the tunability of subwavelength grating/waveguide structure for Fano resonance, the embedded graphene monolayer was replaced by graphene-dielectric stack as a buffer layer. The improved structure was simulated by using the method of rigorous coupled-wave analysis. Nanoscale dielectric thickness in each stack cell can strengthen the effects of the alteration of graphene's conductivity on the equivalent permittivity of stack structure. The results show that, if the system is exploited as an efficient photoswitch, the demanded change of chemical potential of grapheme decreases from original 0.06eV down to 0.02eV and the modulation depth of the switch is up to 94%. If the system is employed as a tunable absorber, the frequency modulation depth of absorption spectrum is raised from 0.14THz to 0.36THz and the tuning range is extended greatly. The improved structure strengthens the tunability of system for Fano resonance.
-
-
![]()
Figure 2. Relationship between transmittance and frequency with different graphene chemical potentials
![]()
Figure 4. Normalized field profiles at the frequency of 4.99THz
a—without grating b—with grating
![]()
Figure 5. Relationship between absorbance and frequency with grating under different chemical potentials
-
[1] HE M D, WANG K J, WANG L, et al.Graphene-based terahertz tunable plasmonics directional coupler[J]. Applied Physics Letters, 2014, 105(8):081903. http://d.old.wanfangdata.com.cn/Periodical/wlxb201714028
[2] DONGY F, LIUP G, YU D W, et al. Dual-band reconfigurable terahertz patch antenna with graphene-stack-based backing cavity[J]. IEEE Antennas & Wireless Propagation Letters, 2016, 15:1541-1544. http://ieeexplore.ieee.org/document/7415987/
[3] ANDRYIEUSKI A, LAVRINENKO A V.Graphenemetamaterials based tunable terahertz absorber:effective surface conductivity approach[J]. Optics Express, 2013, 21(7):9144-9155. http://www.ncbi.nlm.nih.gov/pubmed/23572003
[4] GUO C C, ZHU Z H, YUAN X D, et al. Experimental demonstration of total absorption over 99% in the near infrared for monolayer-graphene-based subwavelength structures[J]. Advanced Optical Materials, 2016, 4(2):1955-1960. DOI: 10.1002/adom.201600481/pdf
[5] ZHOU W D, ZHAO D Y, SHUAI Y C, et al.Progress in 2-D photonic crystal Fano resonance photonics[J]. Progress in Quantum Electronics, 2014, 38(1):1-74. DOI: 10.1016/j.pquantelec.2014.01.001
[6] ZHENG H Y, HU F R. Design of narrowband guided-mode resonance filters in visible wavelength region[J]. Laser Technology, 2016, 40(1):118-121(in Chinese). http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS201601027.htm
[7] WANG Q, ZHANG D W, CHEN J B, et al. Recent progress of guided-mode resonance filters[J]. Laser Technology, 2010, 34(1):71-74(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201001001
[8] GRANDE M, VINCENTI M A, STOMEO T, et al. Graphene-based perfect optical absorbers harnessing guided mode resonances[J]. Optics Express, 2015, 23(16):21032-21042. http://europepmc.org/abstract/MED/26367955
[9] MIZUTANI A, KIKUTA H, LWATA K. Numerical study on an asymmetric guided-mode resonant grating with a Kerr medium for optical switching[J]. Journal of the Optical Society of America, 2005, A22(2):355-360. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b8de1eb87d9a160edd48f0ef4a454ca3
[10] FARHAT M, ROCKSTUHL C, BAGCI H. A 3-D tunable and multi-frequency grapheme plasmonic cloak[J]. Optics Express, 2013, 21(10):12592-12603. http://www.ncbi.nlm.nih.gov/pubmed/23736478
[11] MOHARAM M G, GRANN E B, POMMET D A.Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J]. Journal of the Optical Society of America, 1995, A12(5):1068-1076. http://www.tandfonline.com/servlet/linkout?suffix=CIT0013&dbid=16&doi=10.1080%2F09500340408230413&key=10.1364%2FJOSAA.12.001068
[12] JONES M H, JONES S H. The general properties of Si, Ge, SiGe, SiO2 and Si3N4[EB/OL].[2017-03-24]. http://www.virginiasemi.com/pdf/generalpropertiessi62002.pdf.
[13] PIPER J R, LIU V, FAN S H. Total absorption by degenerate critical coupling[J]. Applied Physics Letters, 2014, 104(25):251110. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e815173e62026af075918cf6ace613ca
[14] EI-NAGGAR S A. Tunable terahertz omnidirectional photonic gap in one dimensional graphene-based photonic crystal[J]. Optical and Quantum Electronics, 2015, 47(7):1627-1636. DOI: 10.1007/s11082-014-0021-1
[15] WANG S S, MAGNUSSON R.Theory and applications of guided-mode resonance filters[J]. Applied Optics, 1993, 32(14):2608-2613. DOI: 10.1364-AO.32.002606/
[16] SANG T, WANG Zh S, WU Y G, et al. Research on guided-mode resonance for sub-wavelength dielectric grating[J]. Acta Photonica Sinica, 2006, 35(5):641-645(in Chinese).
下载:
计量
- 文章访问数: 4
- HTML全文浏览量: 0
- PDF下载量: 4