网站地图
下载:
-
多波长激光在激光光谱学、激光遥感遥测、光电对抗、激光显示、非线性光学频率变换以及激光医学等领域具有广泛的应用，实现双波长激光输出在光纤激光器、固体激光器和二极管激光器领域均有报道[1-5]。二极管激光器不仅具有较宽的波长范围和较高的转换效率，它在体积和重量方面也具有较为出色的表现，并且它的制作成本也相对较低。近年来，基于体布喇格光栅(volume Bragg grating, VBG)的外腔二极管激光器受到关注，它具有输出波长稳定、光谱线窄、结构简单等一系列优点，这主要受益于一种新型的体布喇格光栅[6-8]，这种光栅使用了一种吸收系数非常小的光致热敏材料，这种材料在大功率激光照射情况下仍具有很好的热稳定性和较高的可靠性，这种特性使它在高功率激光系统中被广泛应用。另外，相移体布喇格光栅、多重体布喇格光栅、纵向啁啾体布喇格光栅和横向啁啾体布喇格光栅(transversely chirped volume Bragg grating, TCVBG)等新型体布喇格光栅的特性正在逐步被拓展应用到新的领域[9-12]。其中，横向啁啾体布喇格光栅的中心衍射波长可以根据横向位置的变化实现线性的连续的调节，它不仅具有体布喇格光栅的优点，如可以根据特定的需求设计衍射波长和衍射效率等，它还可以实现不同啁啾波长范围的定制，并且仅仅通过调节光束在横向啁啾体布喇格光栅上的照射位置，就能够非常容易地获取所需波长的衍射，这些优良的特性使其在波长线性且连续可调的应用领域具有非常好的前景[13-16]。
为了研究双体布喇格光栅外腔二极管激光器对输出光谱的影响，作者提出使用横向啁啾体布喇格光栅对其进行了实验验证，首先分析了体布喇格光栅及横向啁啾体布喇格光栅的衍射特性；然后，使用基于光致热敏材料的反射型体布喇格光栅和横向啁啾体布喇格光栅共同外腔二极管激光器实现双波长的输出，通过横向移动其中的一块横向啁啾体布喇格光栅，实验研究横向啁啾体布喇格光栅在不同横向位置时，双体布喇格光栅外腔二极管激光器的输出光谱特性和功率稳定情况。
-
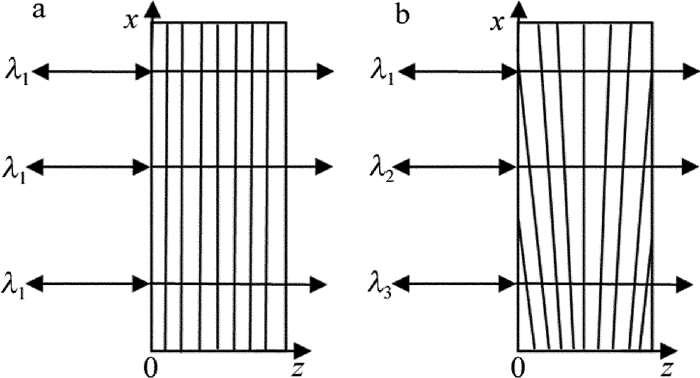
图 1中给出了体布喇格光栅与横向啁啾体布喇格光栅的结构示意图及其对不同波长入射光的衍射特性，两种光栅的折射率分布均可表示为[17]:
$ n = {n_0} + \Delta n{\rm{cos}}\left[ {\frac{{2{\rm{ \mathsf{ π} }}}}{{\mathit{\Lambda }\left( \mathit{x} \right)}}\vec e \cdot \vec z + \varphi } \right] $
(1) 
Figure 1. Diffraction scheme of gratings
式中，n0为光栅的背景折射率，Δn为折射率调制的幅度，φ为余弦函数的相位，Λ(x)为光栅的折射率调制周期，${\vec e} $为光栅矢量，方向垂直于体布喇格光栅的z=0表平面，在图 1中，对于普通的体布喇格光栅，它是一个常数，而由于横向啁啾体布喇格光栅的折射率调制周期Λ和它的横向位置有关，因此，对于横向啁啾体布喇格光栅来说，它是一个关于x的函数。由布喇格条件λ=2n0Λ(x)cosθ可知，在光栅的背景折射率n0和布喇格角θ不变的情况下，对于体布喇格光栅来说，由于它的折射率调制周期与x无关而保持不变，它的布喇格波长也将保持不变，但是横向啁啾体布喇格光栅的布喇格波长λ在光栅的横向方向x轴上呈线性的变化。
体布喇格光栅的衍射效率可以通过KOGELNIK的理论[17]求解，当一束光以满足布喇格条件入射时，它的衍射效率可表示为[18]:
$ \eta (\Delta \lambda ) = {\left\{ {1 + \frac{{1 - {{\left( {\frac{{{\lambda _0}{f^2}\Delta \lambda }}{{2{n_0}\Delta n}}} \right)}^2}}}{{{\rm{sin}}{{\rm{h}}^2}{{\left[ {{{\left( {\frac{{2{\rm{ \mathsf{ π} }}{n_0}t\Delta n}}{{{\lambda _0}^2f}}} \right)}^2} - {{\left( {\frac{{{\rm{ \mathsf{ π} }}ft\Delta \lambda }}{{{\lambda _0}}}} \right)}^2}} \right]}^{1/2}}}}} \right\}^{ - 1}} $
(2) 式中，t是体布喇格光栅的厚度，f是体布喇格光栅的空间频率，f=1/Λ，Δλ为入射光的波长与体布喇格光栅中心波长λ0的偏差。
当Δλ=0时，可得衍射效率的最大值[18]:
$ {\eta _0} = {\rm{tan}}{{\rm{h}}^2}\left( {\frac{{{\rm{ \mathsf{ π} }}t\Delta n}}{{{\lambda _0}\left| {{\rm{cos}}\theta } \right|}}} \right) $
(3) 由于横向啁啾体布喇格光栅的折射率调制周期和它的横向位置有关，具有一定光斑大小和功率分布的光束照射到光栅表面，横向啁啾体布喇格光栅对它的衍射效率应该是不同位置的衍射效率的积分[19]，它的衍射效率可表示为:
$ R = {\int {\left| {\frac{{B\left( {x, y, z = 0} \right)}}{{A(x, y, z = 0)}}} \right|} ^2}{\rm{d}}x{\rm{d}}y $
(4) 式中，A(x, y)和B(x, y)分别是在z=0平面上的入射光场分布和衍射光场分布。
对于体布喇格光栅与横向啁啾体布喇格光栅组成的双光栅而言，由于两块光栅的吸收系数非常小，可以忽略不计，且横向啁啾体布喇格光栅与体布喇格光栅的距离及二者的参量很难满足相移光栅的条件，因此，两块体布喇格光栅组成双体光栅后的衍射效率可表示为:
$ \begin{array}{l} \;\eta \left( \lambda \right) = {\eta _{{\rm{VBG}},1}}(\lambda ) + \\ \frac{{{{\left[ {1 - {\eta _{{\rm{VBG}},1}}(\lambda )} \right]}^2}{\eta _{{\rm{VBG}},2}}\left( \lambda \right)}}{{1 - {\eta _{{\rm{VBG}},1}}(\lambda ){\eta _{{\rm{VBG,2}}}}(\lambda )}} \end{array} $
(5) 式中，ηVBG, 1(λ)是体布喇格光栅的衍射效率，ηVBG, 2(λ)是横向啁啾体布喇格光栅的衍射效率。
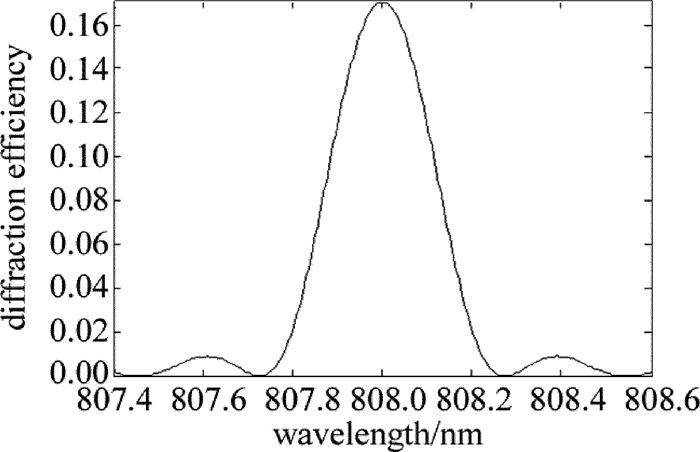
使用波长为808nm的光束为例分析体布喇格光栅的光谱衍射特性，当光栅厚度为0.6mm、折射率调制幅值为229×10-6、调制周期为220nm时，体布喇格光栅的光谱衍射特性曲线如图 2所示。其峰值衍射效率约为17%，光谱选择宽度为0.30nm。
Figure 2. Diffraction curves of volume Bragg grating with central wavelength of 808nm
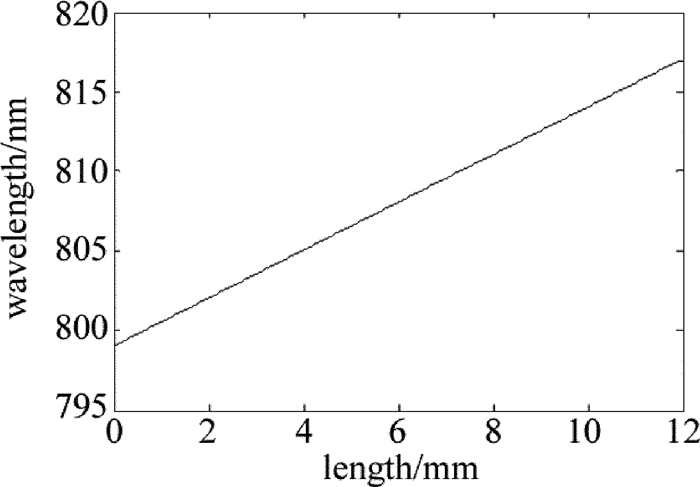
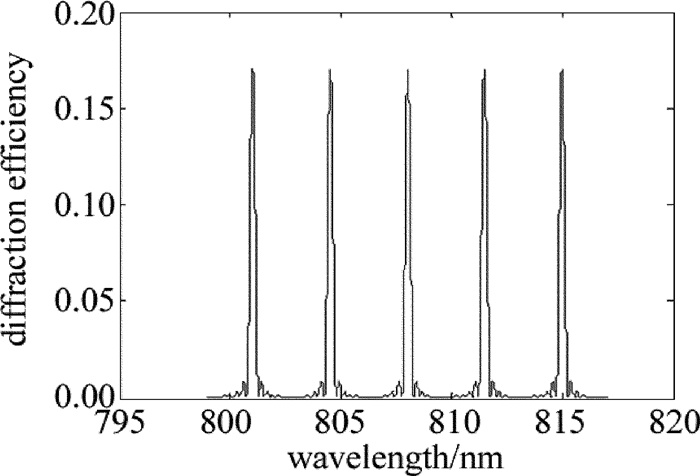
使用波长啁啾系数为1.5nm/mm、啁啾波长位于799nm~817nm之间的横向啁啾体布喇格光栅为研究对象分析横向啁啾体布喇格光栅的衍射特性，当栅厚度为0.69mm、背景折射率为1.4891、折射率调制系数为165×10-6时，图 3中给出了它的横向位置与中心波长的关系，图 4中给出了它在799nm~817nm之间的几个衍射曲线。由理论计算可知，线性啁啾范围内的几条衍射曲线特性几乎没有差别。
Figure 3. Relationship between lateral position and central wavelength of transverse volume Bragg grating
Figure 4. Relationship between diffraction efficiency and central wavelength of transverse chirp Bragg grating
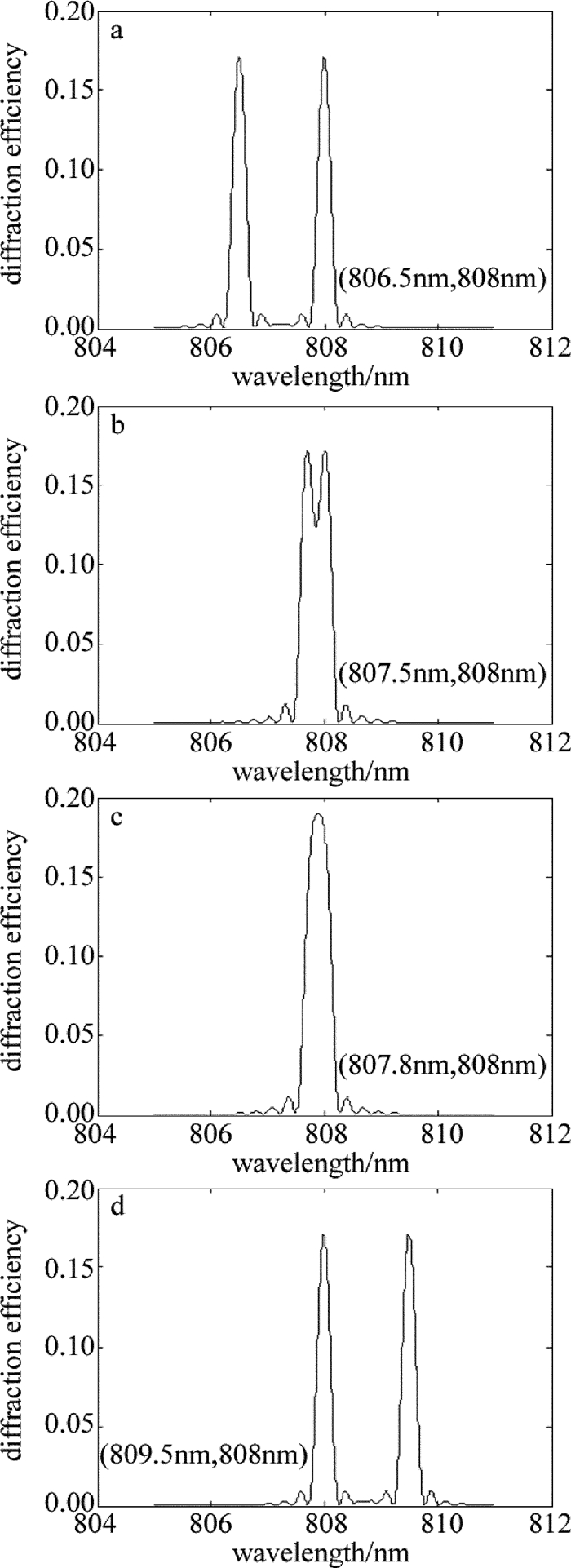
假设体布喇格光栅和横向啁啾体布喇格光栅组成双光栅，通过横向移动横向啁啾体布喇格光栅，计算双光栅在体布喇格光栅一侧的衍射特性，其中，体布喇格光栅和横向啁啾体布喇格光栅的峰值衍射效率均为17%，光谱选择宽度均为0.3nm。当体布喇格光栅和横向啁啾体布喇格光栅组成双光栅后，通过横向移动横向啁啾体布喇格光栅，由(5)式所计算出的在体布喇格光栅一侧的衍射效率如图 5所示。在图 5中，当两块光栅的衍射曲线的主瓣没有重叠时，由(5)式可知，横向啁啾体布喇格光栅的衍射特性基本没有受体布喇格光栅的影响，它们的峰值衍射效率和光谱选择宽度没有变化，如图 5a和图 5d所示；当两个光栅的主瓣存在重叠，且中心波长的差值大于它们的光谱宽度0.3nm时，衍射曲线是一个具有双峰的光谱，如图 5b所示，它的光谱宽度大于0.3nm，随着两个中心波长的差值向0.3nm靠近，光谱宽度逐步减小，并且双峰也会慢慢靠近并消失变为一个峰值；当两个光栅的中心波长差值小于它们的光谱宽度0.3nm时，衍射曲线变成了具有一个峰值的光谱，如图 5c所示，在光谱宽度减小的同时，单峰的衍射效率随着中心波长差值的减小而升高，当它们的中心波长一样时，峰值衍射效率达到了29%。
Figure 5. Relationship between diffraction efficiency and wavelength difference of dual volume Bragg gratings
-
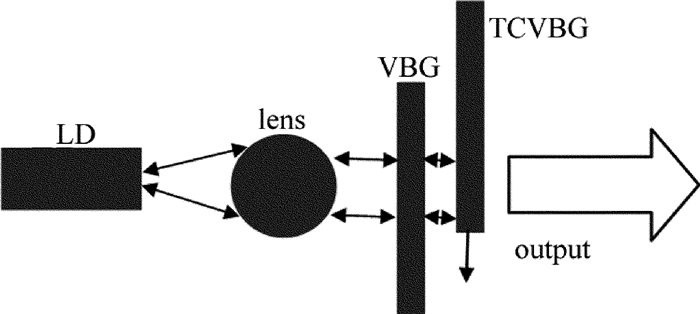
由体布喇格光栅和横向啁啾体布喇格光栅组成的双体布喇格光栅外腔二极管激光器结构包括：一块由半导体致冷器(thermo electric cooler, TEC)进行致冷控温的条宽为200μm且镀有增透膜的二极管激光器(前腔面透过率大于95%)、直径为120μm的圆柱形快轴准直透镜(可将90%的能量集中于8mrad以内)、一块尺寸为0.6mm×1.5mm×12mm的反射式体布喇格光栅(峰值衍射效率约为15%，光谱选择宽度约为0.3nm)和一块尺寸为1.6mm×1.5mm×12mm的横向啁啾体布喇格光栅(啁啾系数为1.5nm/mm，起始啁啾波长为799nm，终止啁啾波长为817nm，峰值衍射效率约为17%，光谱选择宽度约为0.3nm)，如图 6所示。其中，二极管激光器的封装模式为C-Mount封装。两块体布喇格光栅紧贴后体布喇格光栅一侧紧靠二极管激光器，并垂直于输出激光放置。使用两块体布喇格光栅同时反馈时，可同时输出双波长。当横向移动啁啾体布喇格光栅时，可以实现其中一路波长的连续调谐。
Figure 6. Structure diagram of experimental setup
-
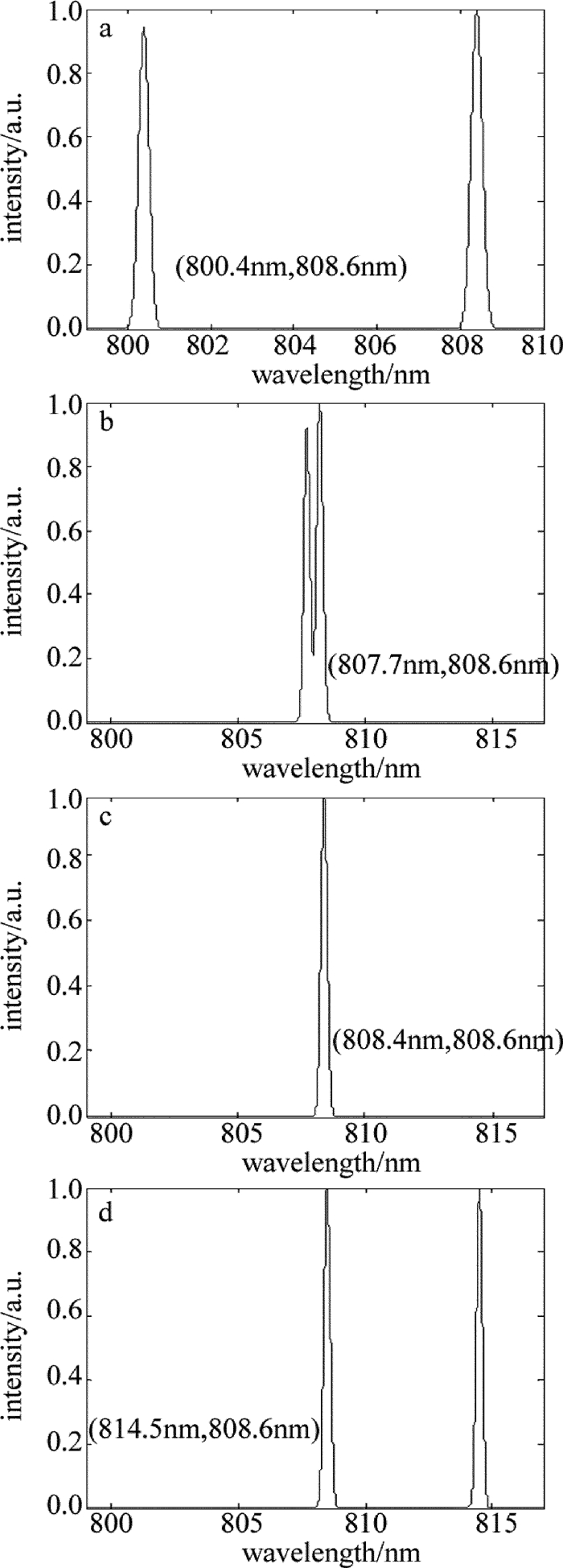
图 7中给出了二极管激光器的温度控制在25℃、驱动电流为3A时，双体布喇格光栅外腔二极管激光器在不同情况下的光谱曲线。实验中采用的光谱仪型号为Avaspec-3648, 其分辨率优于0.10nm。当移动横向啁啾体布喇格光栅，使之光谱选择的中心波长从800nm~815nm变化时，输出波长中的一个波长保持808.6nm附近，另一个中心波长随之从800nm~815nm变化。当横向啁啾体布喇格光栅的光谱选择中心波长为800.4nm时，输出激光的光谱包含800.4nm和808.6nm两个光谱，如图 7a所示，其中800.4nm的谱宽约为0.29nm，中心波长为808.6nm的谱宽约为0.28nm；移动横向啁啾体布喇格光栅的中心波长，使之接近体布喇格光栅的中心波长时，输出波长呈双峰输出，如图 7b所示，此时，由横向啁啾体布喇格光栅稳定的中心波长为807.7nm，由体布喇格光栅稳定的中心波长为808.6nm，由于两个光谱存在重叠部分，输出谱宽较宽；继续移动横向啁啾体布喇格光栅，使之中心波长与体布喇格光栅的中心波长完全重合时，双波长输出变为单波长输出，在中心波长为808.6nm处的输出谱宽约为0.20nm，如图 7c所示，这主要是由于二者的布喇格波长一致时，增强了808.6nm的反馈强度；横向啁啾体布喇格光栅的中心波长向长波长方向继续移动到814.5nm时，中心波长为814.5nm的谱宽约为0.3nm，而由体布喇格光栅稳定的中心波长为808.6nm，其谱宽保持在0.3nm，如图 7d所示。从图中可以看出，双体布喇格光栅二极管激光器中，在保持体布喇格光栅不动的情况下，横向啁啾体布喇格光栅仍可以实现第2个中心波长的连续调谐，且在横向啁啾体布喇格光栅的调谐过程中，并未对体布喇格光栅的中心波长和谱宽造成较大影响。
Figure 7. Relationship between intensity and wavelength difference of external cavity diode laser based on double volume Bragg gratings
值得说明的是，由于横向啁啾体布喇格光栅的厚度(1.6mm)比体布喇格光栅的厚度(0.6mm)大，若将其放置在二极管激光器和体布喇格光栅之间时，加大了体布喇格光栅外腔的腔长，此时，不太容易实现体布喇格光栅对中心波长为808.6nm的光谱锁定，需要多次调整两块光栅的角度，才能实现稳定的双波长输出。另外，当驱动电流为3A时，双体布喇格光栅外腔二极管激光器的输出功率基本维持在1.9W以上，外腔效率约为75%以上，从图 7可以看出，二者的功率比基本控制一个较好的范围内，最差为中心波长分别为800.4nm和808.6nm时，功率比P(800.4nm)/P(808.6nm)≈ 0.945，但是在实验中，降低驱动电流至2.5A，在移动横向啁啾体布喇格光栅的过程中，功率比会出现相差很大的情况，继续降低驱动电流，会出现双波长不易被锁定的情况。
-
利用一块常规体布喇格光栅与一块横向啁啾体布喇格光栅共同作为反馈元件，研究了双体布喇格光栅外腔二极管激光器的光谱特性，当移动横向啁啾体布喇格光栅时，其中一个波长保持不变，而另一个波长可实现800nm~815nm线性可调。在需要同时输出两个波长时，可以采用两块横向啁啾体布喇格光栅作为外腔来实现。
双体光栅外腔二极管激光器光谱特性研究
Study on spectral characteristics of external cavity diode lasers based on dual volume Bragg gratings
-
摘要: 为了研究双体布喇格光栅外腔二极管激光器的衍射特性，采用一块体布喇格光栅与一块横向啁啾体布喇格光栅组成双体布喇格光栅，理论分析了组合前后体布喇格光栅的衍射特性，实验研究了双体布喇格光栅外腔二极管激光器的输出光谱特性。结果表明，在双体布喇格光栅外腔反馈的作用下，可以实现双波长同时输出，通过横向移动横向啁啾体布喇格光栅，可以在保持其中一个中心波长不变的情况下，使另外的一个波长在800nm~815nm的范围内线性调谐。此研究为基于双体布喇格光栅实现双波长输出的大功率二极管激光器提供了实验指导。
-
关键词:
- 激光器 /
- 横向啁啾体布喇格光栅 /
- 双波长 /
- 波长调谐 /
- 外腔
Abstract: In order to study diffraction characteristics of an external cavity diode laser based on dual volume Bragg gratings, a Bragg grating and a transversely chirped Bragg grating were used to compose the dual volume Bragg gratings. The diffraction characteristics of the volume Bragg gratings before and after the combination were analyzed theoretically. The output spectral characteristics of the external cavity diode laser based on dual volume Bragg gratings were studied. The experimental results show that, under the action of the external cavity feedback of the dual volume Bragg gratings, the dual wavelengths can be output simultaneously. By moving the transversely chirped Bragg grating in the lateral direction, it is possible to keep the other one wavelength tuning linearly in the range of 800nm~815nm. This study provides experimental guidance for high-power diode lasers based on dual volume Bragg gratings for dual wavelength output.-
Key words:
- lasers /
- transverse chirped Bragg grating /
- dual wavelength /
- tunable wavelength /
- external cavity
-
Figure 1. Diffraction scheme of gratings
a—volume Bragg grating b—transverse chirped volume Bragg grating
Figure 3. Relationship between lateral position and central wavelength of transverse volume Bragg grating
Figure 4. Relationship between diffraction efficiency and central wavelength of transverse chirp Bragg grating
Figure 5. Relationship between diffraction efficiency and wavelength difference of dual volume Bragg gratings
-
[1] BAI Y B, XIANG W H, ZU P, et al. Tunable two wavelengths linear-cavity Yb-doped fiber laser based on volume grating[J]. Chinese Journal of Lasers, 2011, 38(11):1102004(in Chinese). doi: 10.3788/CJL [2] XU P, HU Zh L, MA L N, et al. Output power stability of dual-wavelength erbium-doped fiber ring laser[J]. Chinese Journal of Lasers, 2009, 36(6):1347-1351(in Chinese). doi: 10.3788/JCL [3] LIU Y G, FENG X H, DONG X Y. Progress in room-temperature stable multi-wavelength fiber laser technologies[J]. Chinese Journal Lasers, 2007, 34(7):883-894(in Chinese). [4] MA J Sh. 3-wavelength operation of an external cavity laser diode with cascaded fiber bragg gratings[J]. Acta Photonica Sinica, 2008, 37(7):1305-1308(in Chinese). [5] CHENG Y, LU Ch Y, LIU X, et al. Dual-wavelength switchable solid state laser[J]. Chinese Journal Lasers, 2010, 37(9):2299-2302(in Chinese). doi: 10.3788/CJL [6] CIAPURIN I V, GLEBOV L B, SMIRNOV V. Spectral combining of high-power fiber laser beams using Bragg grating in PTR glass[J]. Proceedigs of the SPIE, 2004, 5335:116-124. doi: 10.1117/12.533740 [7] ANDRUSYAK O, SMIRNOV V, VENUS G, et al. Beam combining of lasers with high spectral density using volume Bragg gratings[J]. Optics Communications, 2009, 282(13):2560-2563. doi: 10.1016/j.optcom.2009.03.019 [8] ZHAN S B, ZHAO S H, CHU X C, et al. Spectral beam combining of fiber lasers based on a transmitting volume Bragg gratings[J]. Optics & Laser Technology, 2010, 42(2):308-312. [9] JULIEN L, VADIM S, LEODNID B G. Phase-shifted volume Bragg gratings in photo-thermo-refractive glass[J]. Proceedigs of the SPIE, 2008, 6890:68900A. [10] ZOLOTOVSKAYA S A, SMIRNOV V I, VENUS G B, et al. Two-color output from InGaAs laser with multiplexed reflective Bragg mirror[J]. IEEE Photoonics Technology Letters, 2009, 21(10):1093-1095. [11] WANG J Zh, WANG Y F, BAI H J. Diffraction characteristics of longitudinal chirped volume grating based on transfer matrix algorithm[J]. Laser Technology, 2015, 39(1):61-64(in Chinese). [12] WANG J Zh, WANG Y F, BAI H J. A kind of narrow line width external cavity laser diode with wavelength stability and continuous tuning[J]. Chinese Journal of Lasers, 2014, 41(12):1202002(in Chinese). doi: 10.3788/CJL [13] SEGER K, JACOBSSON B, PASISKEVICIUS V, et al. Tunable Yb:KYW laser using a transversely chirped volume Bragg grating[J]. Optics Express, 2009, 17(4):2341-2347. doi: 10.1364/OE.17.002341 [14] JACOBSSON B, PASISKEVICIUS V, LAURELL F, et al. Tunable narrowband optical parametric oscillator using a transversely chirped Bragg grating[J]. Optics Letters, 2009, 34(4):449-451. doi: 10.1364/OL.34.000449 [15] ZEIL P, PASISKENVICIUS V, LAURELL F. Efficient spectral control and tuning of a high power narrow-linewidth Yb-doped fiber laser using a transversely chirped volume Bragg grating[J]. Optics Express, 2013, 21(4):4027-4035. doi: 10.1364/OE.21.004027 [16] CHANN B, GOYAL A K, FAN T Y, et al. Efficient high-brightness wavelength-beam-combined commercial off-the-shelf diode stacks achieved by use of a wavelength-chirped volume Bragg grating[J]. Optics Letters, 2006, 31(9):1253-1255. doi: 10.1364/OL.31.001253 [17] KOGELNIK H. Coupled wave theory for thick hologram gratings[J]. The Bell System Technical Journal, 1969, 48(9):2909-2945. doi: 10.1002/bltj.1969.48.issue-9 [18] CIAPURIN I V, GLEBOV L B, SMIRNOV V I. Modeling of Gaussian beam diffraction on volume Bragg gratings in PTR glass[J]. Proceedigs of the SPIE, 2005, 5742:183-193. doi: 10.1117/12.591215 [19] WANG J Zh, WANG Y F, YU X F, et al. Study of spectral characteristics of external cavity diode laser using transversely chirped volume Bragg grating[J]. Chinese Journal of Lasers, 2015, 42(5):0515002(in Chinese). doi: 10.3788/CJL -
点击查看大图
图(7)
计量
- 文章访问数: 8239
- HTML全文浏览量: 6106
- PDF下载量: 152
- 被引次数: 0
