Optimization of fast image encryption algorithm based on chaotic mapping
-
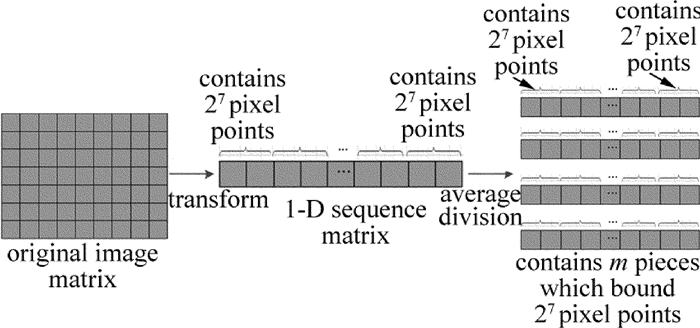
摘要: 为了解决现有图像加密算法存在随图像尺寸变大导致加密时间迅速增加的问题，采用基于logistic和Arnold映射的改进加密算法实现了快速图像加密算法的优化。该算法基于两种混沌映射对原文图像进行像素置乱和灰度值替代，像素置乱是按图像大小选择以H个相邻像素为单位进行，通过适当调整H的取值实现加密时间优化；灰度值替代是利用Arnold映射产生混沌序列对置乱图像进行操作而得到密文图像。结果表明，对于256×256的Lena标准图像，加密时间降低到0.0817s。该算法具有密钥空间大和加密速度快等优点，能有效抵抗穷举、统计和差分等方式的攻击。Abstract: In order to solve the rapid increase of the encryption time because of the increasing image size in the existing image encryption algorithm, the optimized encryption algorithm based on logistic and Arnold mapping was used to achieve the optimization of the fast image encryption algorithm. The algorithm was based on two kinds of chaotic maps to the original image, pixel scrambling and gray value substitution. Pixel scrambling was to select the H adjacent pixels according to the image size, appropriately adjust the H value and realize the encryption time optimization. Gray value substitution is to generate chaotic sequences by Arnold mapping, operate the scrambling image and get the cipher image. The results show that, for 256×256 Lena standard images, the encryption time is reduced to 0.0817s. The algorithm has advantages of large key space and fast encryption speed, and can effectively resist the attack of exhaustive, statistical, and differential means.
-
Keywords:
- image processing /
- image encryption /
- chaotic mapping /
- Lena image
-
-
![]()
Figure 4. Encryption and decryption results
a—original image b—cipher image c—decryption image d—the decryption image by the wrong key with x0+10-12
![]()
Figure 7. Correlation between adjacent pixels of the original and encrypted image
a—horizontal of original image b—horizontal of encrypted image c—vertical of original image d—vertical of encrypted image e—diagonal direction of original image f—diagonal direction of encrypted image
![]()
Table 1 Information entropy of different images
Lena.tiff Baboon.tiff Peppers.tiff original image 7.4451 7.3583 7.5937 cipher image 7.9973 7.9972 7.9973 
下载: 导出CSV
Table 2 Average value of NPCR and UACI in different encrypted images
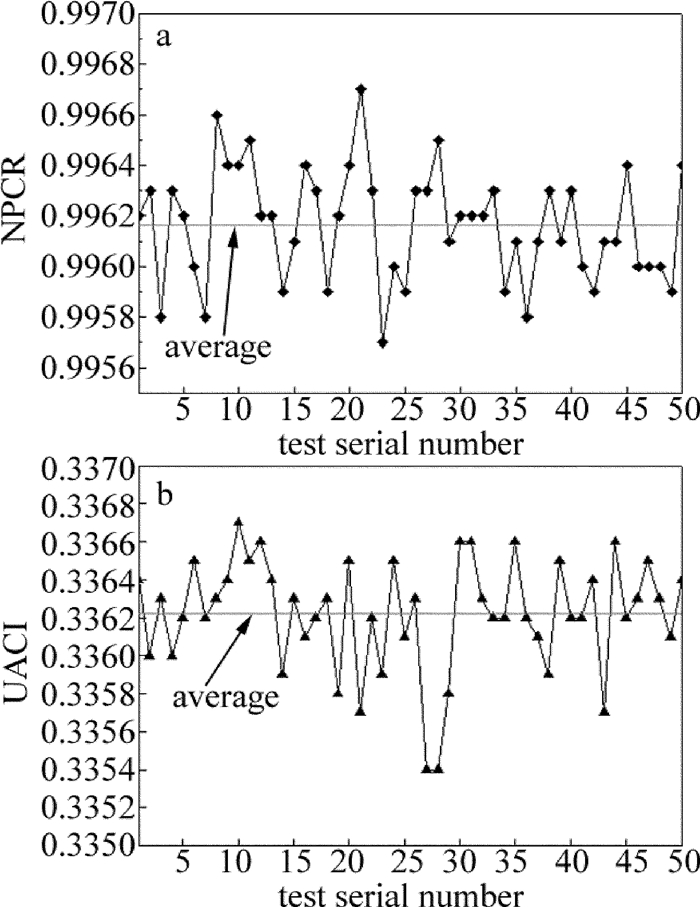
Lena.tiff Baboon.tiff Peppers.tiff Airplane.tiff ¯NNPCR 0.9962 0.9961 0.9960 0.9961 ¯UUACI 0.3362 0.3349 0.3357 0.3351
下载: 导出CSV
Table 3 Comparison of the correlation coefficients between the algorithm with the adjacent pixels and the other algorithms
下载: 导出CSV
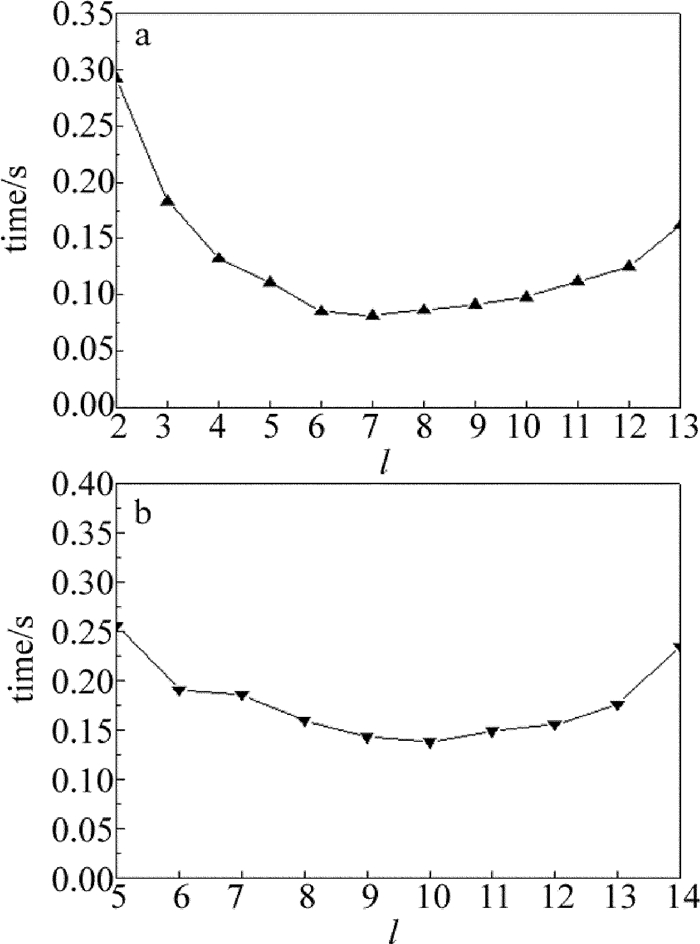
Table 5 Performance parameters for different l values
l information entropy NPCR UACI vertical horizontal diagonal encryption speeds/s 2 7.9975 0.9962 0.3345 -0.0027 0.0050 8.9480×10-4 0.2979 3 7.9975 0.9960 0.3344 0.0021 0.0013 0.0045 0.1964 4 7.9973 0.9965 0.3350 -0.9782×10-4 0.0025 0.0026 0.1318 5 7.9973 0.9961 0.3342 -0.0048 -0.0023 -0.0027 0.1127 6 7.9968 0.9961 0.3351 0.0052 -9.5974×10-4 0.0042 0.0828 7 7.9973 0.9962 0.3362 -0.0028 0.0054 -4.4027×10-4 0.0817 8 7.9975 0.9962 0.3346 -0.0020 0.0037 1.3699×10-4 0.0832 9 7.9970 09961 0.3345 1.9570×10-4 0.0088 0.0048 0.0843 10 7.9964 0.9961 0.3342 0.0013 0.0028 -0.0040 0.0896 11 7.9970 0.9962 0.3353 5.3722×10-4 -0.0079 0.0046 0.1097 12 7.9972 0.9962 0.3355 -0.0044 -0.0010 8.4257×10-4 0.1295 13 7.9972 0.9963 0.3353 -0.0025 6.8750×10-4 -9.7786×10-4 0.1591
下载: 导出CSV
-
[1] XU G X, XU Sh Q, GUO X J, et al. Image compression-encryption algorithm combined DCT transform with DNA operation[J]. Laser Technology, 2015, 39(6):806-810 (in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201506016
[2] ZHU C X, SUN K H. Encryption algorithm for a class of hyper chaotic image encryption algorithm and its improvement[J]. Acta Physica Sinica, 2012, 61(12):120503(in Chinese).
[3] WANG X Y, LIU L T, ZHANG Y Q. A novel chaotic block image encryption algorithm based on dynamic random growth technique[J]. Optics & Lasers in Engineering, 2015, 66(66):10-18. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3e1db2d845601c172f5016209669d772
[4] ZHANG W, YU H, ZHAO Z L, et al. Image encryption based on three-dimensional bit matrix permutation[J]. Signal Processing, 2016, 118(3): 36-50. http://www.sciencedirect.com/science/article/pii/S0165168415002078
[5] ZHOU Y C, BAO L, CHEN P C L. A new 1-D chaotic system for image encryption [J].Signal Processing, 2014, 97(7): 172-182. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=950941f486c31664f98529f5c8abf9c3
[6] REN X K, MA Ch. Improvement and implementation of 3D color image encryption[J].Microellectronics & Computer, 2015, 32(1): 96-99(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/wdzxyjsj201501021
[7] WANG L Y, SONG H J, LIU P. A novel hybrid color image encryption algorithm using two complex chaotic systems[J]. Optics and Lasers in Engineering, 2016, 77(15): 118-125. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7b3c5a841680aa50669a2e503d29b1cd
[8] LI F Y, XU J F. Image encryption algorithm based on Hash function and multi chaotic system[J].Computer Engineering and Design, 2010, 31(1): 141-144(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-SJSJ201001039.htm
[9] ZHENG H Y, LI W J, XIAO D. Novel image blocking encryption algorithm based on spatiotemporal chaos system[J].Journal of Computer Application, 2011, 31(11): 3053-3055(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjyy201111047
[10] WANG Ch L, WU X J. Fractional order chaotic color image encryption algorithm based on block scrambling and diffusion[J].Journal of Henan University(Natural Science Edition), 2014, 44(6): 715-724(in Chinese).
[11] LIU P, YAN Ch, HUANG X G. Improved generation method of chaotic spread spectrum sequence based on Logistic map[J]. Journal of Communication, 2007, 28(2):134-140(in Chinese).
[12] GU G S, LING J. A fast image encryption method by using chaotic 3-D cat maps[J]. Optik—International Journal for Light and Electron Optics, 2014, 124(17):4700-4705. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2b112bf121c764bb9cb43a66a3fcfa17
[13] WANG X Y, LIU L T, ZHANG Y Q. A novel chaotic block image encryption algorithm based on dynamic random growth technique[J]. Optics & Lasers in Engineering, 2015, 66(3):10-18. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3e1db2d845601c172f5016209669d772
[14] ZHAO J F, WANG S Y, CHANG Y X, et al. A novel image encryption scheme based on an improper fractional-order chaotic system[J]. Nonlinear Dynamics, 2015, 80(4):1721-1729. DOI: 10.1007/s11071-015-1911-x
[15] WU Y. NPCR and UACI randomness tests for image encryption [J]. Cyber Journals: Journal of Selected Areas in Telecommunications, 2011, 4(1):1-8.
[16] PATIDAR V, PAREEK N K, SUD K K. A new substitution-diffusion based image cipher using chaotic standard and logistic maps[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14 (7): 3056-3075. DOI: 10.1016/j.cnsns.2008.11.005
[17] WANG X Y, WANG Q. A novel image encryption algorithm based on dynamic S-boxes constructed by chaos[J].Nonlinear Dynamics, 2014, 75(3):567-576. DOI: 10.1007/s11071-013-1086-2
[18] LI L, WANG W N, LI J J. Security improvement for image encryption algorithm based on hyper-chaotic system[J]. Application Research of Computer, 2011, 28(11): 4335-4337(in Chinese).
[19] YE R S. A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism [J]. Optics Communications, 2011, 284(22): 5290-5298. DOI: 10.1016/j.optcom.2011.07.070
计量
- 文章访问数: 9
- HTML全文浏览量: 0
- PDF下载量: 3