网站地图
下载:
-
弹幕武器通常采用多管形式的小口径转管炮。由于射频快，射击时前后的冲击振动相互影响，复杂的炮口振动是影响弹幕武器弹丸散布的重要原因之一。不同身管之间射击的振动情况交叉影响且不易安装辅助测量设备，其炮口振动情况比常规火炮更为复杂，振动信号的时域波形比较复杂，例如低频率的扰动只有几十赫兹，而身管壁的弹性振动，尤其是身管应力波的频率可达千赫兹量级，这种信号要求测试系统具有频响宽、动态范围大、分辨率高、适应复杂环境的测试特点[1-5]。现有测试方法如接触式传感器的测量，其原理简单、操作简便，但会改变炮口振动状态，且对于转管火炮而言，接触式传感器安装难度大；非接触式测量方法如光电位移跟随器、电涡流传感器、相位敏感探测器(phase sensitive detector, PSD)三角位移测量、电荷耦合器件(charge coupled device, CCD)位移传感器、高速摄影等，主要存在测量距离过近、易被身管后坐或炮口冲击损坏、测量精度低、需要在身管上加装辅助测量设备等问题，难以完成弹幕武器炮口振动测试。
激光散斑计量技术是在多学科基础上发展起来的现代光学测量方法。激光散斑计量技术不仅具有传统光学测量方法高精度、高灵敏度等特点[6-9]，而且对测量环境的要求低、无需在身管上安装辅助测量设备、能够实现远距离测量，在解决弹幕武器炮口振动中具有很大的应用前景。
本文中基于雪崩光电二极管(avalanche photo diode, APD)弱信号检测和线激光技术，研究基于线激光散斑光电检测技术的弹幕武器炮口振动测量方法，旨在实现在无需辅助测量设备情况下的复杂时域炮口振动信号测试问题。
-
线激光器照射炮口效果如图 1所示。将点激光整形成线激光后[10-13]，照射到测量位置，线激光光斑的长度大于身管直径，因此在测试过程中，身管能够一直处于线激光的覆盖范围，避免了光斑脱离身管或者需要加装辅助测量装置的影响。
Figure 1. Muzzle imaging irradiated by 650nm line laser
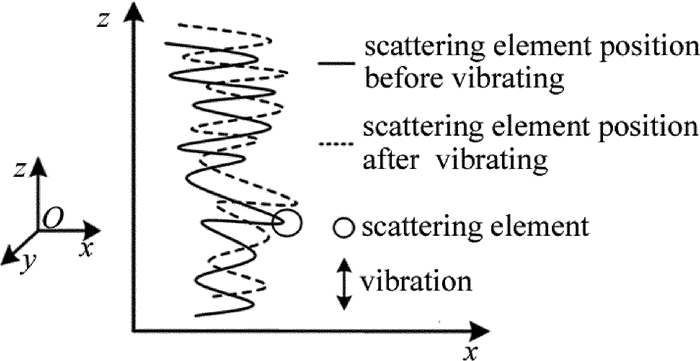
图 2为目标物做面内振动时，物体表面在微尺度上的一个典型截面示意图。这些表面散射基元的随机性对物体表面粗糙度有着决定性影响。此时，振动引起物体散射基元沿振动方向发生位移，引起被照射表面区域的一部分早先散射基元运动到照射区域之外，同时一些新的散射基元移进来代替它们，造成被照射表面区域的表面高度标准差发生变化，使被照射区域的表面粗糙度发生变化，经由粗糙表面上不同基元反射回来的光波发生变化，导致其干涉产生的散斑也发生变化，如图 3所示，具体表现为散斑场内部的斑点运动。
Figure 2. Schematic diagram of surface profile when the object is in plane vibration
Figure 3. Diagram of speckle frequency shift
若目标物做离面振动，同样引起物体散射基元沿振动方向发生位移，造成由散射基元反射回来的光波发生变化，导致其干涉产生的散斑也发生变化，具体表现为散斑场内部的斑点频移(即斑点的运动)。总体来说，振动会引起散斑场变化，散斑斑点的频移中携带有目标的振动特性信息。
-
在图 3中，假设经振动体表面漫反射后，激光散斑的频移为Δνd，偏振方向相同的参考光和测量光垂直照射在光电检测器件的光敏面上，其光电场Er(t)和Em(t)分别为[14-15]：
$ {{E}_{\text{r}}}(t)={{E}_{\text{r}, 0}}\text{cos}(2\text{ }\!\!\pi\!\!\text{ }\nu t+{{\varphi }_{\text{r}}}) $
(1) $ {{E}_{\text{m}}}(t)={{E}_{\text{m}, 0}}\text{cos}[2\text{ }\!\!\pi\!\!\text{ }(\nu +\Delta {{\nu }_{\text{d}}})t+{{\varphi }_{\text{m}}}]~ $
(2) 式中，φr和φm分别表示参考光和测量光的散斑移动相位，可得光电检测器的输出电流ip(t)为：
$ {{i}_{\text{p}}}\left( t \right)=\alpha {{\left[ {{E}_{\text{m}}}\left( t \right)+{{E}_{\text{r}}}\left( t \right) \right]}^{2}}~ $
(3) 代入(1)式和(2)式得出[4]：
$ \begin{align} &{{i}_{\text{p}}}\left( t \right)=\alpha \{{{E}_{\text{r}, 0}}^{2}\text{co}{{\text{s}}^{2}}(2\text{ }\!\!\pi\!\!\text{ }\nu t+{{\varphi }_{r}})+ \\ &~{{E}_{\text{m}, 0}}^{2}\text{co}{{\text{s}}^{2}}[2\text{ }\!\!\pi\!\!\text{ }(\nu +\Delta {{\nu }_{\text{d}}})t+{{\varphi }_{\text{m}}}]+~ \\ &{{E}_{\text{r, }0}}{{E}_{\text{m}, 0}}\text{cos}[2\text{ }\!\!\pi\!\!\text{ }(2\nu +\Delta {{\nu }_{\text{d}}})t+{{\varphi }_{\text{r}}}+{{\varphi }_{\text{m}}}]+~ \\ &{{E}_{\text{r}, 0}}{{E}_{\text{m}, 0}}\text{cos}[2\text{ }\!\!\pi\!\!\text{ }\Delta {{\nu }_{\text{d}}}t+{{\varphi }_{\text{r}}}-{{\varphi }_{\text{m}}}]\}~ \\ \end{align} $
(4) 式中，α=eη/(hν)为光电转换系数，e为电子电量, hν为光子能量，η为探测器的量子效率。
由于光电探测器件的响应速率有限，对于光频信号，只能检测其平均值。因此(4)式中的前3项均为直流分量，第4项为差频项。经直流滤波后，探测器输出的瞬时电流信号为：
$ i\left( t \right)=\alpha {{E}_{\text{r}, 0}}{{E}_{\text{m}, 0}}\text{cos}\left( 2\text{ }\!\!\pi\!\!\text{ }\Delta {{\nu }_{\text{d}}}t+{{\varphi }_{\text{r}}}-{{\varphi }_{\text{m}}} \right)~ $
(5) 假设测量目标的瞬时振动函数可表示为V(t), 则瞬时散斑频移可表示为[5]：
$ \Delta {{\nu }_{\text{d}}}=2vV\left( t \right)/c $
(6) 又设λ为激光波长，s(t)为振动目标的瞬时振动位移，令参考光与测量光的初始相位差φ0=φm-φr，则可得探测器输出的瞬时电流信号为：
$ i\left( t \right)=\alpha {{E}_{\text{r},0}}{{E}_{\text{m},0}}\text{cos}\left[ \frac{4\text{ }\text{ }\!\!\pi\!\!\text{ }\text{ }}{\lambda }s\left( t \right)+{{\varphi }_{0}} \right]~ $
(7) 式中，αEr, 0Em, 0可视为一常数。由式中可以看出，i(t)与s(t)存在频率对应关系，振动信号s(t)与光电流i(t)的角频率呈对应关系，相当于振动信号对光电流信号的频率调制。
因此，可以采用频率解调的方法进行测量，通过对散斑斑点的光电检测，从光电流i(t)的频率变化中解调出被测目标表面相关的振动信号。
-
在对散斑斑点信号进行光电检测的过程中，由于漫反射方向的球面特性，散斑场反馈回检测器件的光强非常弱，信号检测困难，微弱信号检测放大电路设计中必须重点考虑电路的噪声抑制能力。
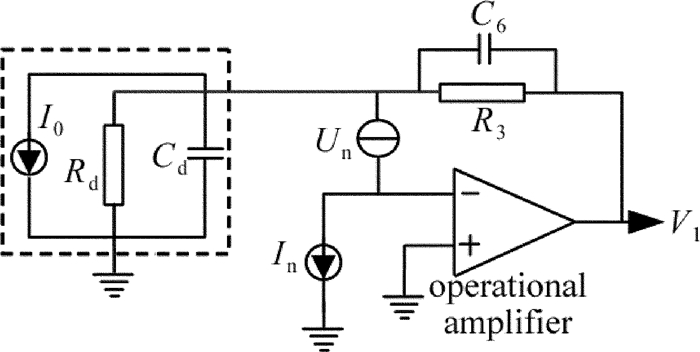
图 4为光电检测电路的噪声源模型，虚线框内为APD的等效电路。Cd为结电容; Rd为等效电阻; In为运放的输入噪声电流, 当偏置电流为皮安量级的超低偏置电流运放时，对一般实用的反馈电阻，该噪声分量可忽略不计[16]; Un为运放的输入噪声电压; C6为消除振动的反馈电容; I0为信号电流; R3为反馈电阻；ω为通用系数。忽略In的影响，则可推导出运放的输出电压为：
$ {{V}_{1}}=\frac{{{R}_{3}}{{I}_{0}}}{1+j\omega {{R}_{3}}{{C}_{6}}}+\left( 1+\frac{{{R}_{3}}}{{{R}_{\text{d}}}}\frac{1+j\omega {{R}_{\text{d}}}{{C}_{\text{d}}}}{1+j\omega {{R}_{3}}{{C}_{6}}} \right){{U}_{\text{n}}} $
(8) 
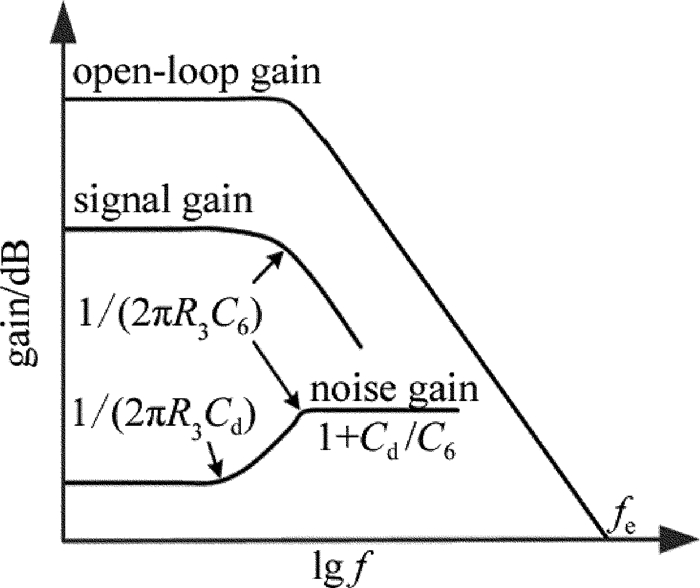
Figure 4. Noise source model of photoelectric detection circuit
根据(8)式给出电路信号增益与噪声增益的幅频特性曲线如图 5所示，其中fe为理论上增益为零时的截止频率。信号电流I0为直流或较低频率时，增益系数的值等于电阻值R3, 随着信号频率的增加，电容C6的影响逐渐增大；频率从1/(2πR3C6)开始，电路放大倍数开始下降，噪声增益开始增加。噪声电压与信号电流的幅频特性则相反：在直流段或较低频率时，增益为1+R3/Rd；随着频率的增加，电路噪声增益由于电容Cd的作用开始升高，直到由于电容C6的作用而停止(转折频率为1/(2πR3C6))，噪声增益限定在1+Cd/C6。
Figure 5. Amplitude frequency characteristics of photoelectric detection circuit
可见，加入C6可以限制高频段的噪声增益，同时也会降低高频段的信号增益。为使保证电流放大电路获得足够的响应频带，需降低电阻R3的阻值，C6也只能取小电容。
对于光电检测器件，其内部噪声主要来源于热噪声和散粒噪声。热噪声电压UT均方值取决于材料的温度，并有如下关系[17-19]：
$ {{U}_{T}}^{2}=4kTR\int_{{{f}_{1}}}^{{{f}_{2}}}{R\left( f \right)\text{d}f}~ $
(9) 式中，k为玻尔兹曼常数，T为温度，f为频率，f1和f2分别表示放大电路的通频带的上限频率和下限频率。在通常温度范围内，热噪声和散粒噪声的频谱均可看作是平直的白噪声。电阻R与频率无关，热噪声的输出取决于检测电路的实际通频带Δf=f2-f1，此时(9)式变为：
$ {{U}_{T}}^{2}=4kTR\Delta f~ $
(10) 由此可见，带宽越大，噪声也越大。所以，需要损失一定的高增益带宽来降低噪声。同时，除运放带入噪声外，反馈电阻R3也是一个重要的噪声源，电阻的热噪声输出取决于检测电路的实际通频带Δf。而且UT与R3成正比，因此R3也不能过大。
-
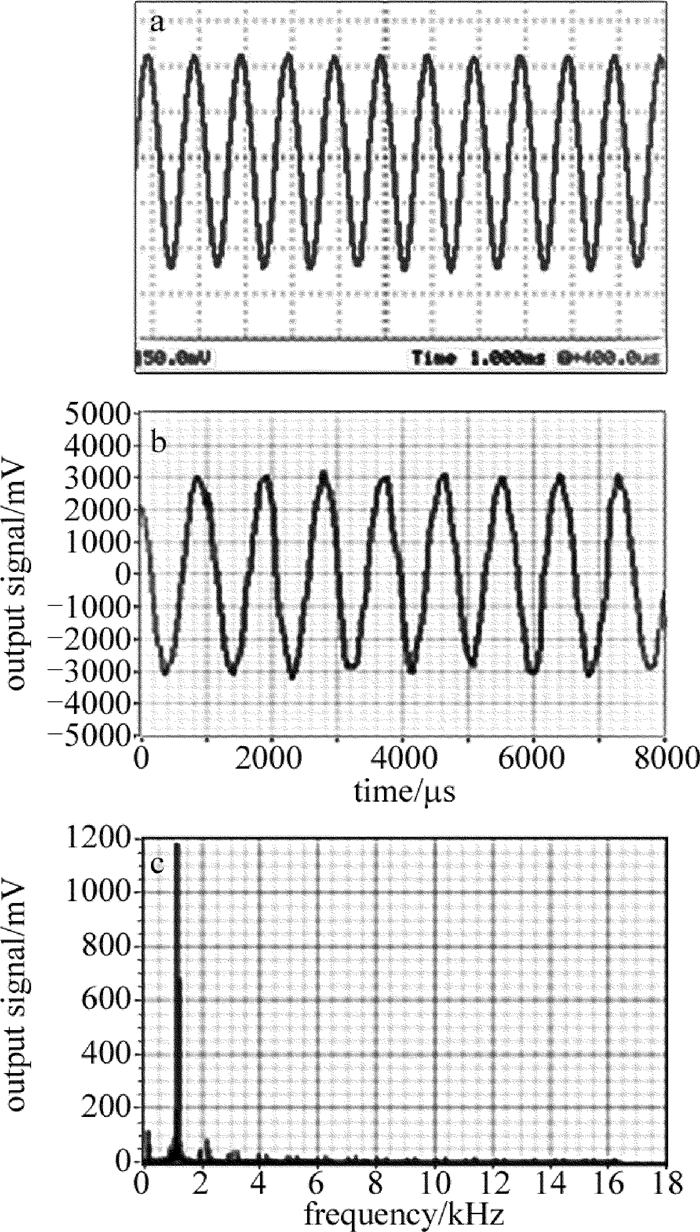
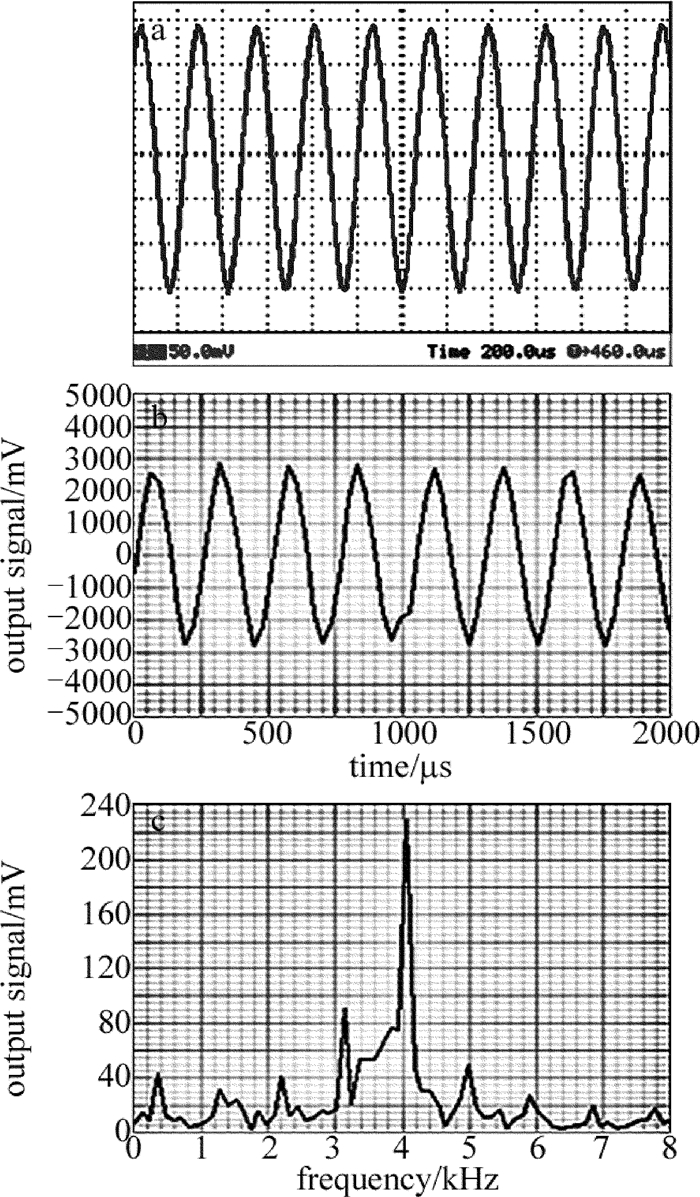
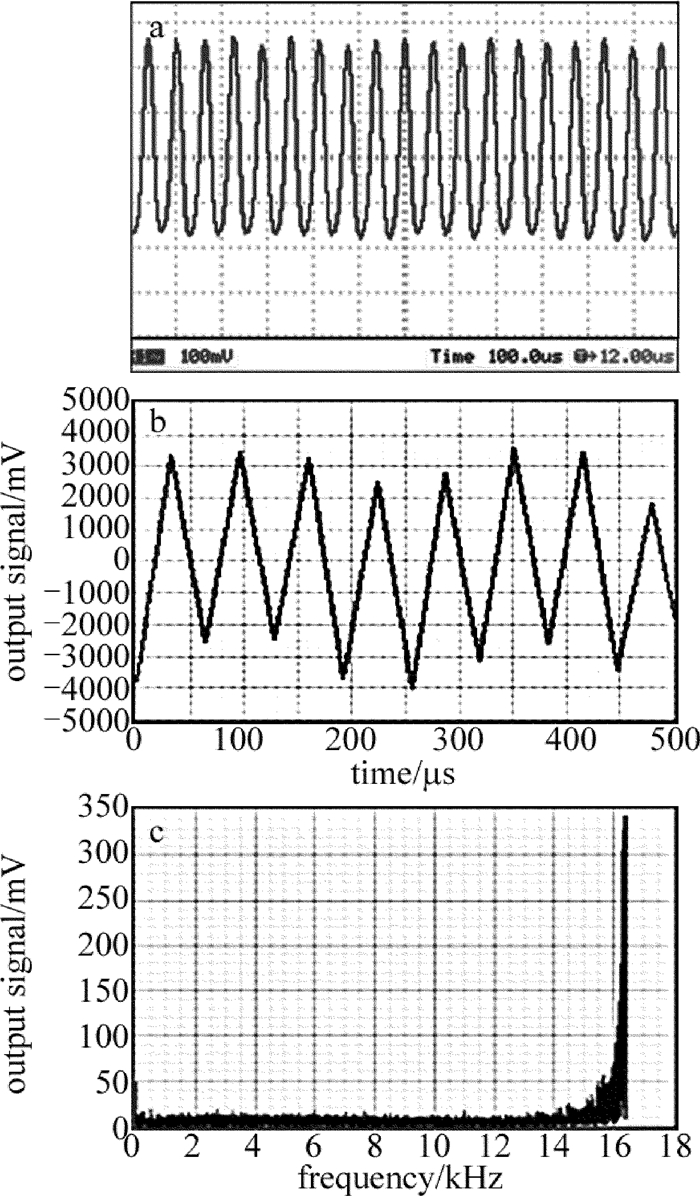
在距离目标较远的距离上开展测量，可以有效避免火炮射击时剧烈振动对测量装置的干扰。实验过程中，测量目标在距测量装置25m远处，通过音频设备对金属面进行激振，激励信号频率在50Hz~16kHz之间，振幅在微米量级。取其中激励信号频率为1kHz, 4kHz, 16kHz时的输出波形和幅频特性如图 6、图 7、图 8所示。从图中可以看出，测量所得的输出信号与激励信号的频率相同，检测电路的信噪比高，具有很好的幅频特性，这实现了对被测目标振动信号的检测。基于线激光散斑检测的炮口振动测量方法具有较好的频率响应特性，能够实现复杂频率振动信号的检测。
Figure 6. Sine wave of excitation signal at 1kHz
Figure 7. Sine wave of excitation signal at 4kHz
Figure 8. Sine wave of excitation signal at 16kHz
-
基于线激光散斑检测的火炮炮口振动测量方法具有对测量环境要求低、无需安装辅助测量设备、可以实现远测量距离等优点，采用线激光取代点激光可以有效克服采用点激光测量时，激光束脱离火炮身管范围导致测量失败的缺点。文中给出的宽幅频特性、高噪声抑制比的APD检测电路在克服火炮发射过程的身管振动所处的恶劣环境，解决复杂频域炮口振动信号测试等问题上具有一定的优势。
线激光散斑检测弹幕武器炮口振动测量方法
Method for measuring muzzle vibration of barrage weapons based on line laser speckle detection
-
摘要: 为了解决在弹幕武器射击时的恶劣环境下，频域分布复杂的炮口振动信号测试难题，采用线激光散斑场光电检测方法，研究了振动信号与输出电流数学关系，分析了基于雪崩光电二极管的光电检测电路噪声与幅频特性，提出了一种基于身管表面线激光散斑效应的炮口振动测量的方法，并进行了25m远处的振幅在微米级、频率为50Hz~16kHz振动信号的检测实验。结果表明，线激光散斑检测炮口振动振幅在微米量级。该测量方法具有频率响应范围宽、测量距离远、灵敏度高等优点，实现了远距离、宽频域振动信号的检测。Abstract: In order to solve the testing problem of muzzle vibration signal with complex frequency distribution under the abominable circumstances with the shooting of barrage weapons, the photoelectric detection method based on line laser speckle field was used. The mathematical relationship between the vibration signal and output current was studied, and the noise and amplitude frequency characteristics of photoelectric detection circuit based on avalanche photo diode were analyzed. A method of muzzle vibration measurement based on laser speckle effect of barrel surface was proposed. The detection experiment of vibration signal was carried out at distance of 25m, with amplitude of micron magnitude and frequency of 50Hz~16kHz. The results show that, the vibration amplitude of gun muzzle is μm magnitude. The measurement method has advantages of wide frequency response range, long measurement distance and high sensitivity. Vibration signal detection at long distance and wide frequency range is realized.
-
Key words:
- measurement and metrology /
- muzzle vibration /
- laser speckle /
- spots shift /
- photoelectric detection
-
Figure 6. Sine wave of excitation signal at 1kHz
a—excitation signal(t=1ms) b—output signal c—amplitude-frequency curve
Figure 7. Sine wave of excitation signal at 4kHz
a—excitation signal(t=250μs) b—output signal c—amplitude-frequency curve
-
[1] CHEN Y H, GUO M, HE Z Y, et al. Muzzle vibration test method and practice [J]. Journal of Gun Launch & Control, 2010, 26(1): 80-83 (in Chinese). [2] HE K P, XU D, LI H. High precision measurement for barrage weapon dispersion based on large area triangle composite light-screens [J]. Optical Precision Engineering, 2015, 23(6): 1523-1529 (in Chinese). doi: 10.3788/OPE. [3] SHI Y D, WANG D Sh. Study on vibration characteristics of barrel subjected to moving projectile considering inertia effect [J]. Acta Armamentarii, 2011, 32(4): 414-420 (in Chinese). [4] ZHU Y H, HE F T, PENG X L. Research of characteristics of laser speckle of plastic optical fiber [J]. Laser Technology, 2016, 40(1): 122-125 (in Chinese). [5] SHI H, ZHU H, WU J, et al. Research on the technique of vibration frequency remote detection based on speckle pattern[J]. Laser Technology, 2016, 40(6): 801-805(in Chinese). [6] HE K P, XU D, LI H. Modularized parallel signal acquisition system design of massive channels for laser screen target [J]. Laser Technology, 2016, 40(6): 810-813 (in Chinese). [7] AYALA G, RIVERA A L, DÁVILA A, et al. Analysis of mechanical vibrations through speckle interferometry: A phase-space approach [J]. Optik, 2010, 28(5): 2028-2035. [8] CAO Y, HE K P, SHAO S J, et al. Anti-saturation design of photoelectric detection circuit in laser simulation resistance system [J]. Laser & Infrared, 2012, 36(8): 925-927 (in Chinese). [9] ZHANG D B, SONG Y H, WANG Q Sh, et al. Error analysis of laser divergence angle measurement [J]. Laser Technology, 2016, 40(6): 926-929 (in Chinese). [10] MOULDER M J, QIAN J, BEDELL H E. Motion deblurring during pursuit tracking improves spatial-interval acuity [J]. Vision Research, 2013, 81(2): 6-11. [11] GENG T Q, NIU Y X, ZHANG Y, et al. Analysis of detection capability of active laser detection systems [J]. Laser Technology, 2015, 39(6): 509-512 (in Chinese). [12] CHEN Ch, GUO X M, MA J, et al. Measurement of surface roughness based on laser angular-speckle correlation method [J]. Laser Technology, 2015, 39(4): 497-500 (in Chinese). [13] SHI Zh H, LIN G Y, WANG Sh R, et al. Numerical analysis of small particle measurement based on the theory of laser scattering [J]. Infrared and Laser Engineering, 2015, 44(7): 2189-2194 (in Chinese). [14] WANG Y H, FENG J Y, WANG X, et al. Shearing speckle interferometry based on slit aperture for dynamic measurement [J]. Optics and Precision Engineering, 2015, 23(3): 645-651 (in Chinese). doi: 10.3788/OPE. [15] CHEN S T, ZHANG Y, HU H F. Surface roughness measurement based on fractal dimension of laser speckle [J]. Chinese Journal of Lasers, 2015, 42(4): 0408002 (in Chinese). doi: 10.3788/CJL [16] WANG B T. Research on zero differential laser vibration technology[D].Chengdu: University of Electronic Science and Technology of China, 2011: 36-38 (in Chinese). [17] LIU H Y, ZHANG Y G, AI Y, et al. Research of balanced detection techniques for high speed weak optical signal [J]. Laser Technology, 2015, 39(2): 182-184 (in Chinese). [18] HUANG L, ZHANG L Ch, YAN R. Application of high-performance GPU computing in digital speckle pattern recognition algorithms [J]. Journal of Applied Optics, 2015, 36(5): 762-767 (in Chinese). doi: 10.5768/JAO201536.0502006 [19] WANG J F, LIU J Y, ZHAO H, et al. An improved sub-pixel positioning method of laser spot center [J]. Laser Technology, 2016, 39(4): 476-479(in Chinese). -
点击查看大图
图(8)
计量
- 文章访问数: 9201
- HTML全文浏览量: 6813
- PDF下载量: 147
- 被引次数: 0
