Numerical study on output characteristics of single-pulse mode-locked fiber lasers
-
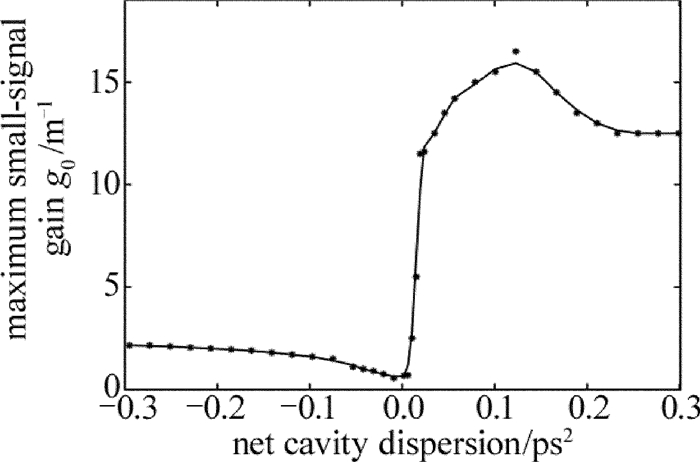
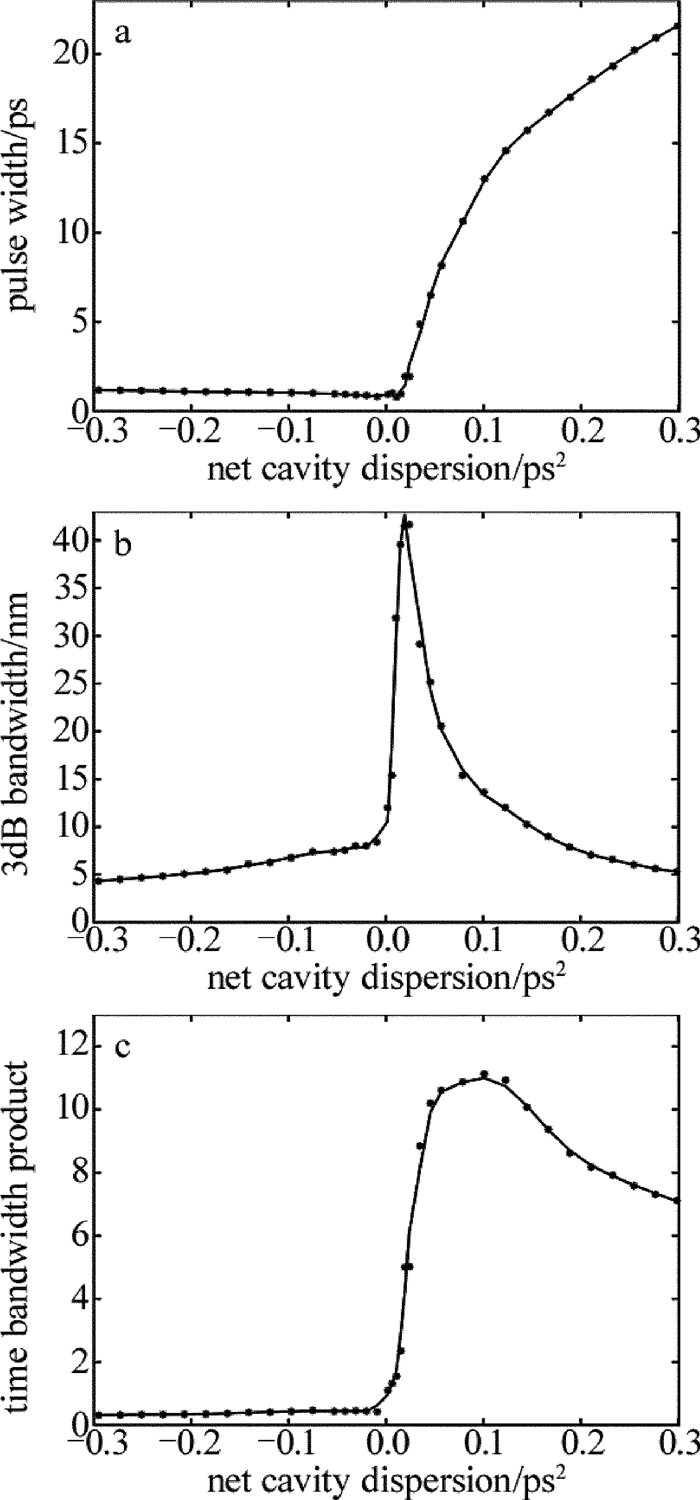
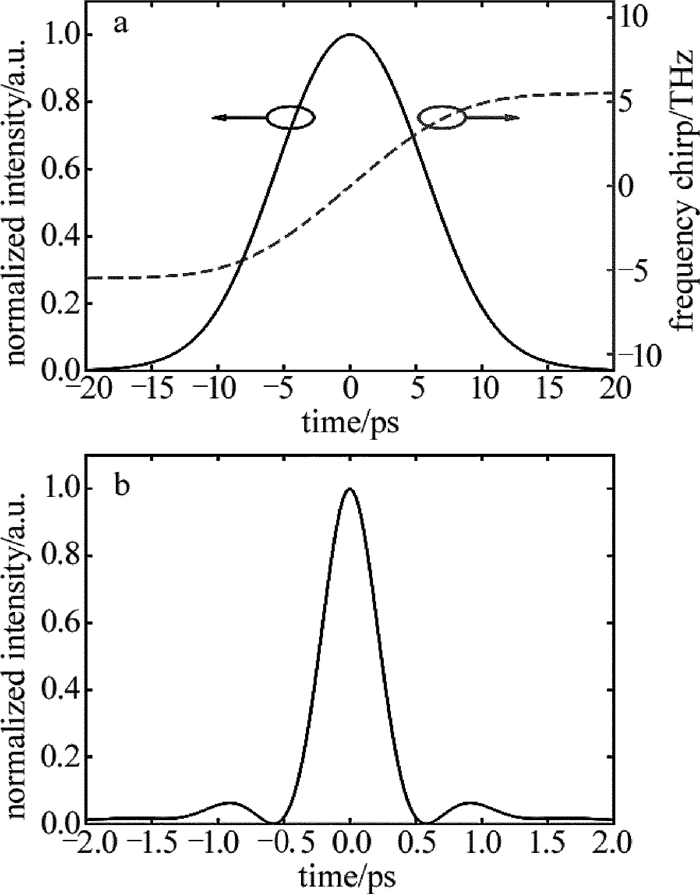
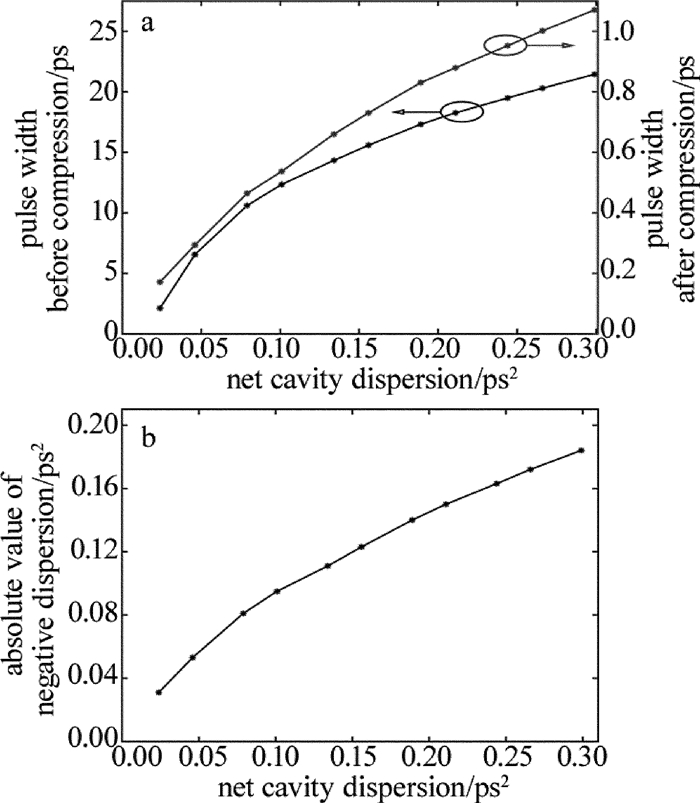
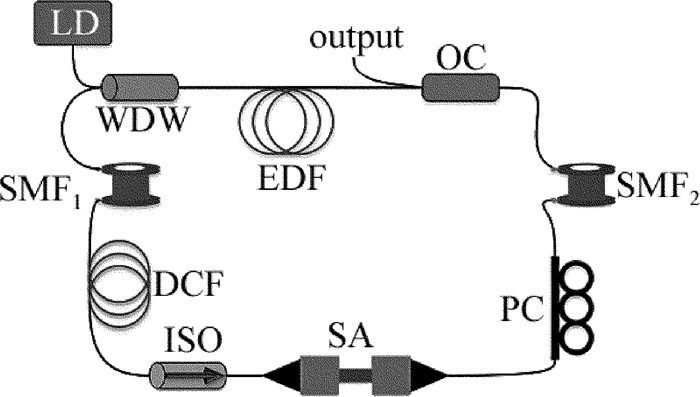
摘要: 为了研究不同腔内净色散下单脉冲被动锁模光纤激光器的输出特性，采用以非线性薛定谔方程为数学模型和分步傅里叶的方法，对激光脉冲在腔内的演化进行了理论分析。获得了在保持单脉冲稳定输出时激光器一些参量与腔内净色散的变化关系，并针对净色散为正的情况，对输出脉冲进行了腔外解啁啾压缩，压缩比达到10倍以上，分析了压缩所需的负色散值以及压缩后脉宽的情况。结果表明，小信号增益系数最大值与净腔色散大体上成正比关系，且当小信号增益系数达到最大值时，输出脉冲的脉宽以及相应的时间带宽积呈现逐渐增加的趋势，3dB带宽则呈现出先增加后减少的趋势。该研究结果为优化被动锁模光纤激光器提供了参考。Abstract: In order to analyze the output characteristics in single-pulse mode-locked fiber lasers with different net cavity dispersion, a numerical model based on the nonlinear Schr dinger equation is conducted to analyze the pulse evolution in the cavity by using the split-step Fourier method. According to the numerical simulation, the relationship between some parameters in fiber lasers and the net cavity dispersion is proven theoretically, and in the case that the net cavity dispersion is positive, the output pulse is compressed outside the cavity numerically and the compression ratio reaches up to ten times. Then the values of the required dispersion and the pulse width after compression are calculated. The results show that the maximum small-signal gain coefficient is proportional to the net cavity dispersion in general. And when the small-signal gain coefficient reaches the maximum value, the pulse width and the time-bandwidth product(TBP) increase gradually, and the 3dB bandwidth increases first and then decreases with the increase of the net cavity dispersion. The conclusion can provide reference for optimizing passively mode-locked fiber lasers.
-
Keywords:
- lasers /
- nonlinear Schr dinger equation /
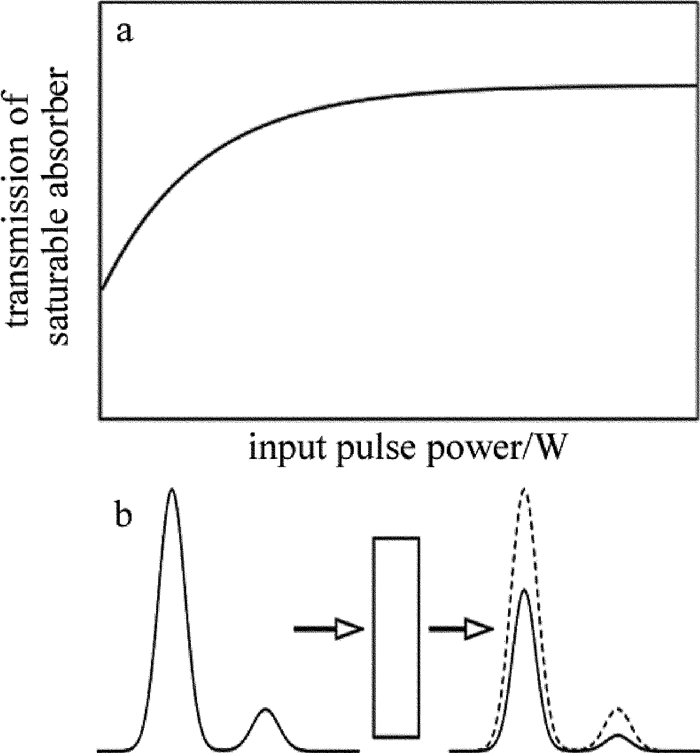
- saturable absorber /
- single pulse /
- chirp
-
-
![]()
Figure 2. a—transmission of saturable absorber b—effect of saturable absorber on pulse
![]()
Figure 6. Temporal shape and chirp information
a—before compression b—after compression
![]()
Figure 7. a—pulse width before compression and after compression b—the required net dispersion outside the cavity with different net cavity dispersions
-
[1] FERMANN M E, HARTL I. Ultrafast fiber laser technology[J].IEEE Journal of Selected Topics in Quantum Electronics, 2009, 15(1):191-206. DOI: 10.1109/JSTQE.2008.2010246
[2] SIBBETT W, LAGATSKY A A, BROWN C T. The development and application of femtosecond laser systems[J]. Optics Express, 2012, 20(7):6989-7001. DOI: 10.1364/OE.20.006989
[3] KALISKY Y. Cr4+:YAG as passive Q-switch and Brewster plate in a pulsed Nd:YAG laser[J]. IEEE Journal of Quantum Electronics, 1995, 31(10):1738-1741. DOI: 10.1109/3.466043
[4] DEMARIA A J, STETSER D A, HEYNAU H. Self mode-locking of lasers with saturable absorbers [J]. Applied Physics Letters, 1966, 8(7):174-176. DOI: 10.1063/1.1754541
[5] ZHAO Y, LIU Y Zh, ZHAO D Sh, et al. Evolution of mode-locked technology of fiber lasers[J]. Laser Technology, 2009, 33(2):162-165(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-JGJS200902017.htm
[6] CABASSE A, MARTEL G, OUDAR J L. High power dissipative soliton in an Erbium-doped fiber laser mode-locked with a high modulation depth saturable absorber mirror[J]. Optics Express, 2009, 17(12):9537-9542. DOI: 10.1364/OE.17.009537
[7] TANG D Y, ZHAO L M. Generation of 47fs pulses directly from an erbium-doped fiber laser[J]. Optics Letters, 2007, 32(1):41-43. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7cc4b6b6cd1e433daa4d29f97e63ce0b
[8] SAKAKIBARA Y, TATSUURA S, KATAURA H, et al. Near-infrared saturable absorption of single-wall carbon nanotubes prepared by laser ablation method[J]. Japanese Journal of Applied Physics, 2003, 42(5A):L494-L496. http://adsabs.harvard.edu/abs/2003JaJAP..42L.494S
[9] SUN Z, HASAN T, TORRISI F, et al. Graphene mode-locked ultrafast laser[J]. ACS Nano, 2009, 4(2):803-810. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0229716118/
[10] XIA H D, LI H P, WANG Z G, et al. Nanosecond pulse generation in a graphene mode-locked erbium-doped fiber laser[J]. Optics Communications, 2014, 330:147-150. DOI: 10.1016/j.optcom.2014.05.048
[11] WANG J, CAI Z, XU P, et al. Pulse dynamics in carbon nanotube mode-locked fiber lasers near zero cavity dispersion[J]. Optics Express, 2015, 23(8):9947-9958. DOI: 10.1364/OE.23.009947
[12] LU H T, WANG F, DENG T. Study of the self-similar evolution for optical pulse in nonlinearity-increasing fibers[J]. Laser Technology, 2010, 34(2):218-220(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201002012
[13] JEON J, LEE J, JU H L. Numerical study on the minimum modulation depth of a saturable absorber for, stable fiber laser mode locking[J]. Journal of the Optical Society of America, 2015, B32(1):31-37. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=efa9a04f1b58df5d7c2e0134a7be2063
[14] AGRAWAL G P. Nonlinear fiber optics[M]. 3th ed. San Diego, California, USA: Academic Press, 2001:39-51.
[15] WISE F W, CHONG A, RENNINGER W H. High-energy femtosecond fiber lasers based on pulse propagation at normal dispersion[J]. Laser & Photonics Reviews, 2008, 2(1/2):58-73. DOI: 10.1002/lpor.200710041/full
-
期刊类型引用(2)
1. 杜鹃, 熊胗婷, 佘敏, 张娇娇, 刘思敏, 张祖兴. 可调谐被动锁模掺铥光纤激光器. 激光技术. 2019(01): 11-14 . 
本站查看
2. 王宁, 冯芳, 赵琳, 沈花玉. 实验室X射线激光输出特性分析与研究. 激光杂志. 2019(09): 177-181 . 百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 6
- HTML全文浏览量: 0
- PDF下载量: 8
- 被引次数: 2