Numerical analysis of thermal effect of the combined laser on single crystal silicon
-
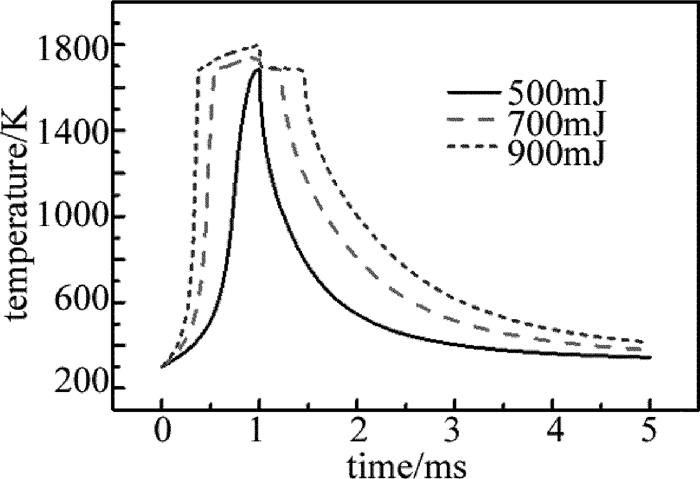
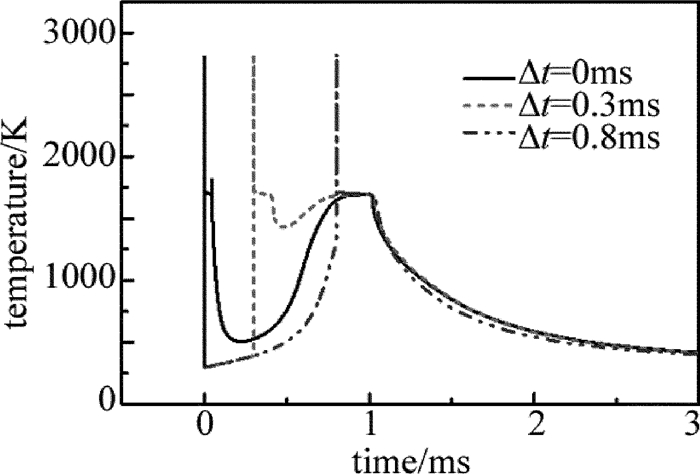
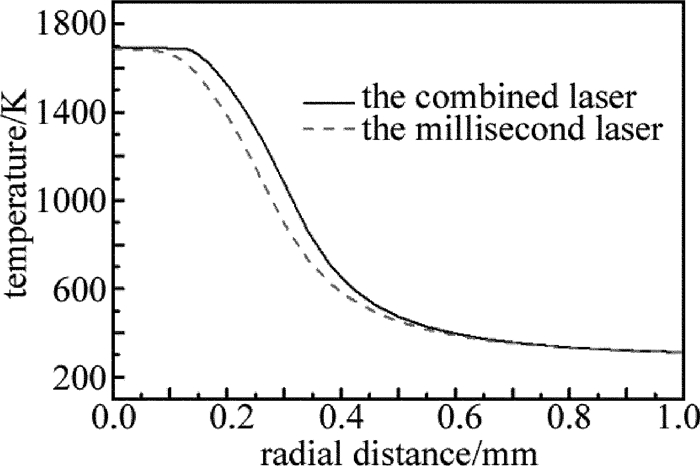
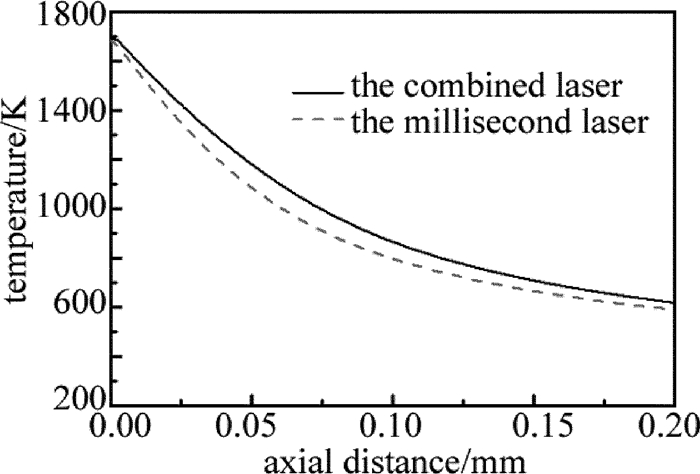
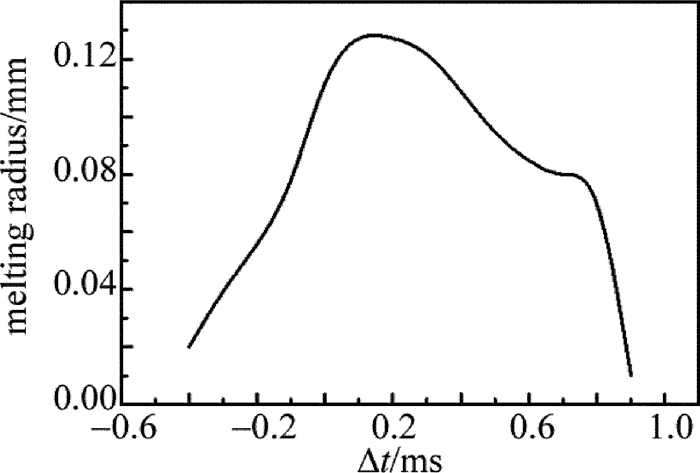
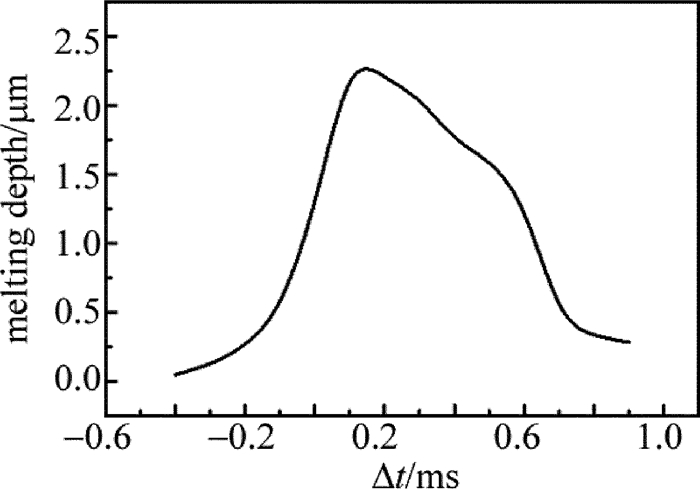
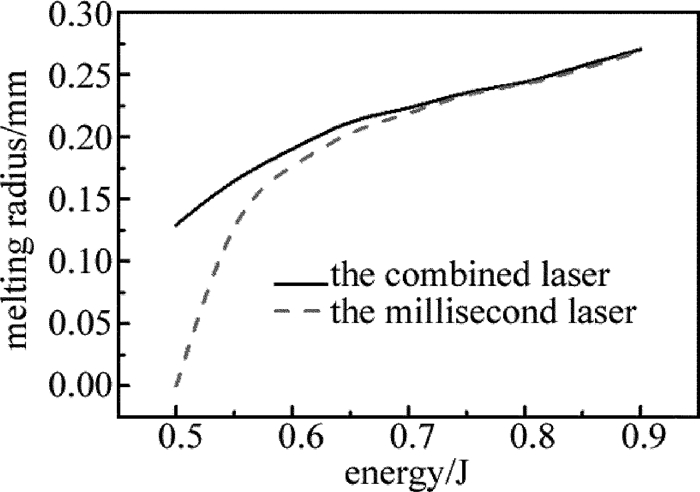
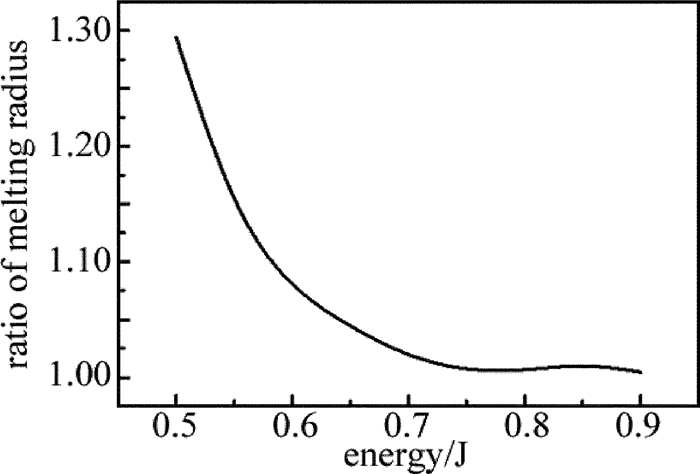
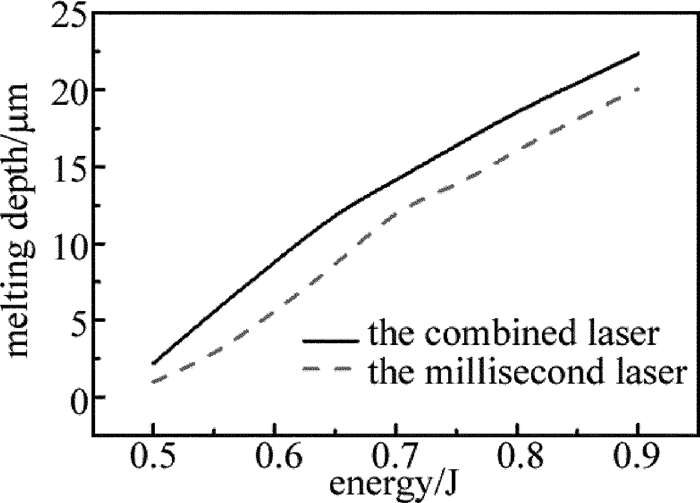
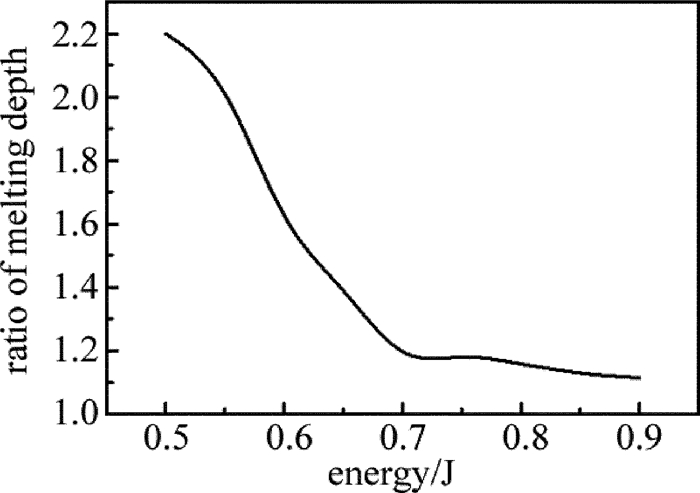
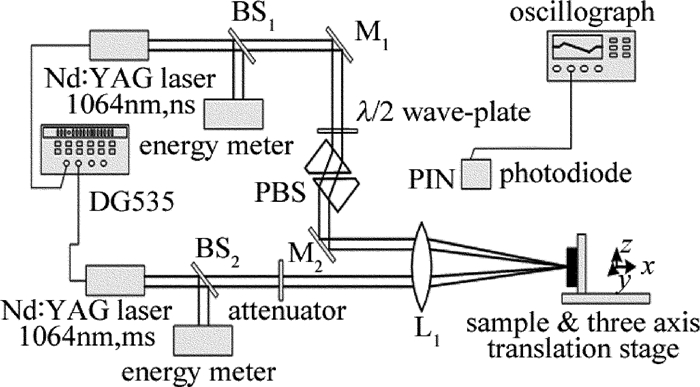
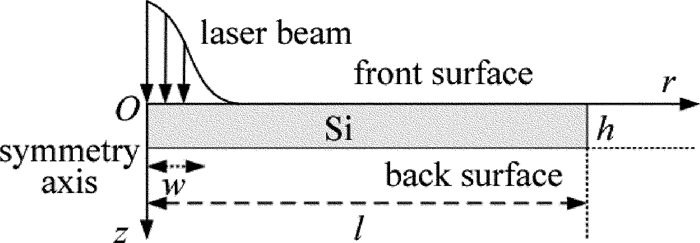
摘要: 为了提高激光加工中单晶硅材料对激光能量的耦合效率，采用一个短脉冲激光和一个长脉冲激光形成组合激光辐照单晶硅，使用COMSOL软件对该过程进行模拟，得到了组合激光长短脉冲间的延迟时间和长脉冲激光能量密度的变化对作用效果的影响，并与总能量相等的毫秒激光单独作用的效果进行比较；实验测量得到的不同能量密度的激光作用单晶硅后损伤形貌，与数值计算结果的趋势吻合。结果表明，组合激光能提高材料对激光的耦合效率；不同的延迟时间会影响组合激光的作用效果，最佳延迟时间为0.1ms；组合激光中毫秒激光能量密度占比较低时，作用效能较明显，随着毫秒激光能量密度占比的提高，对作用效果的提升相对变缓。该研究结果可以为组合激光的应用提供理论和实验依据。Abstract: In order to improve coupling efficiency of laser energy of monocrystalline silicon in laser processing, a short laser pulse and a long laser pulse were used to form a combined pulse to irradiate the monocrystalline silicon. The process was simulated by using COMSOL software. The influences of the delay time of combination laser and the laser energy density of long pulse on the process effect were obtained. The effect was compared with that of individual action millisecond laser under the equal total energy. The measured damage morphologies of monocrystalline silicon irradiated by lasers with different power intensities were in agreement with the trend of numerical results. The results show that the combined laser can improve the coupling efficiency of laser. The different delay time would affect the process effect of the combined laser. The optimum delay time is 0.1ms. When the ratio of the millisecond laser energy density in the combined laser is relatively low, the effect is obvious. With the increase of the ratio of the millisecond laser energy density, the enhancement of the effect is relatively slow. The research results can provide theoretical and experimental basis for the application of combined laser.
-
-
![]()
Figure 2. Relationship between temperature of the center induced by the millisecond laser and time with different energies
![]()
Figure 3. Relationship between temperature of the center induced by the combined laser and Δt with different dalay times
![]()
Figure 4. Relationship between temperature and radial distance after laser irradiation
![]()
Figure 13. Damage morphology
a, c, e, g, i, k—the millisecond laser b, d, f, h, j, l—the combined laser
parameter solid liquid ρ/(kg·m-3) 2330-2.19×10-2T 2540-2.19× 10-2T- 1.21×10-5T2 c/(J·kg-1· K-1) 352.43+1.78T- 2.21×10-3T2+1.3×10-6T3- 2.83×10-10T4 1021.84 κ/(W·m-1· K-1) 299/(T-99) 0.62 R(1064nm) 0.33 0.72 α/m-1 1023×(T/T0)4 8.6×107 
下载: 导出CSV
-
[1] PAN Y, ZHANG H, CHEN J, et al. Millisecond laser machining of transparent materials assisted by nanosecond laser[J]. Optics Express, 2015, 23(2):765-775. DOI: 10.1364/OE.23.000765
[2] LI L Q, CHEN Y B, TAO W. Reserch on dual-beam welding characteristics of aluminum alloy[J]. Chinese Journal of Lasers, 2008, 35(11):1783-1788(in Chinese) DOI: 10.3788/JCL
[3] FORSMAN A C, BANKS P S, PERRY M D, et al. Doublepulse machining as a techniques for the enhancement of material removal rates in laser machining of metals[J]. Journal of Appllied Physics, 2005, 98(3):033302. DOI: 10.1063/1.1996834
[4] WANG X D, MICHALOWSKI A, WALTER D, et al. Laser drilling of stainless steel with nanosecond double-pulse[J]. Optics & Laser Technology, 2009, 41(2):148-153. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0575573f2556b5c2e233f68f5ca24d80
[5] LEHANE C, KWOK H S. Enhanced drilling using a dual-pulse Nd:YAG laser[J]. Applied Physics, 2001, A73(1):45-48. DOI: 10.1007/s003390100819
[6] JIAO L G, ZHAO G M, CHEN M S. Simulation of temperature rise of 45# steel target irradiated by combined laser in the two dimensional cases[J]. Infrared and Laser Engineering, 2010, 39(1):42-46(in Chinese). http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_0dacf8c87c09067a5d11e8082ca8cbb5
[7] JIAO L G, ZHAO G M, CHEN M S. Investigation on the irradiation effects of Q235 steel targets by combined laser[J]. Infrared and Laser Engineering, 2011, 40(5):848-852(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hwyjggc201105015
[8] XIAO Q, HE H X, XIA H J. Stress simulation on aluminium alloy irradiated by long pulsed laser and continuous wave laser[J].Chinese Journal of Lasers, 2012, 39(11):1103002(in Chinese). DOI: 10.3788/CJL
[9] XIAO Q, HE H X, XIA H J.Temprature flied simulation on aluminium alloy irradiated by long pulsed laser and continuous wave laser[J].Chinese Journal of Lasers, 2013, 40(8):0803009(in Chinese). DOI: 10.3788/CJL
[10] WANG X, QIN Y, WANG B, et al. Numerical and experimental study of the thermal stress of silicon induced by a millisecond laser[J]. Applied Optics, 2011, 50(21):3725-3732. DOI: 10.1364/AO.50.003725
[11] LIM D J, KI H, MAZUMDER J. Mass removal modes in the laser ablation of silicon by a Q-switched diode-pumped solid-state laser (DPSSL)[J]. Journal of Physics, 2006, D39(12):2624-2635. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=de0fb6683a5303815108b2bcabe3ea61
[12] MASOLIN A, BOUCHARD P O, MARTINI R, et al. Thermo-mechanical and fracture properties in single-crystal silicon[J]. Journal of Materials Science, 2013, 48(3):979-988. DOI: 10.1007/s10853-012-6713-7
[13] TAO S, WU B X, ZHOU Y, et al. Thermal modeling and experimental study of infrared nanosecond laser ablation of silicon[J]. Journal of Applied Physics, 2009, 106(12):123507. DOI: 10.1063/1.3271413
[14] YAMAGUCHI K, ITAGAKI K. Measurement of high temperature heat content of silicon by drop calorimetry[J]. Journal of Thermal Analysis and Calorimetry, 2002, 69(3):1059-1066. DOI: 10.1023/A:1020609517891
[15] WANG X. The thermal and mechanical effects during pulsed laser interaction with semiconductor materials and the application of laser scribing on the CIGS thin film solar cell[D].Nanjing: Nanjing University of Science and Technology, 2013: 49-50(in Chinese).
计量
- 文章访问数: 4
- HTML全文浏览量: 0
- PDF下载量: 5