Optimized design of grating coupling packaging structure on silicon substrate
-
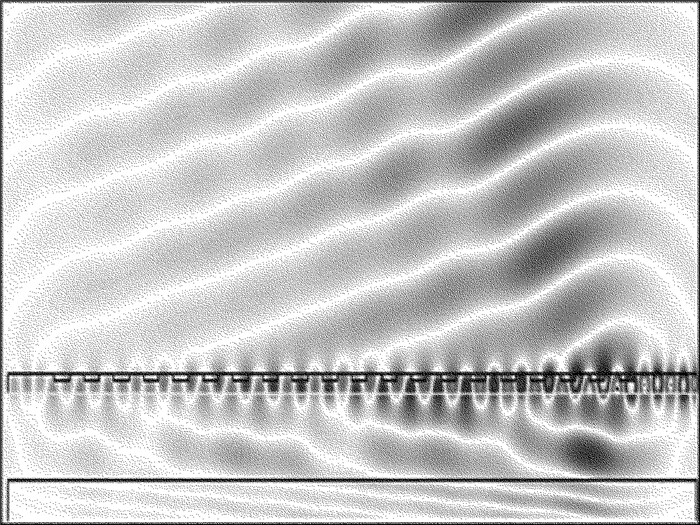
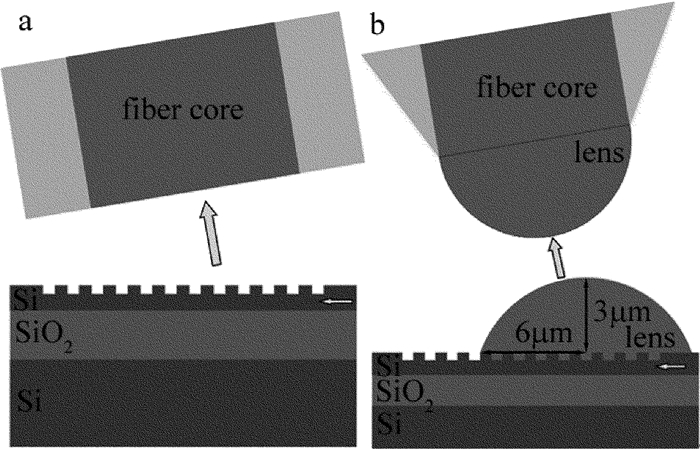
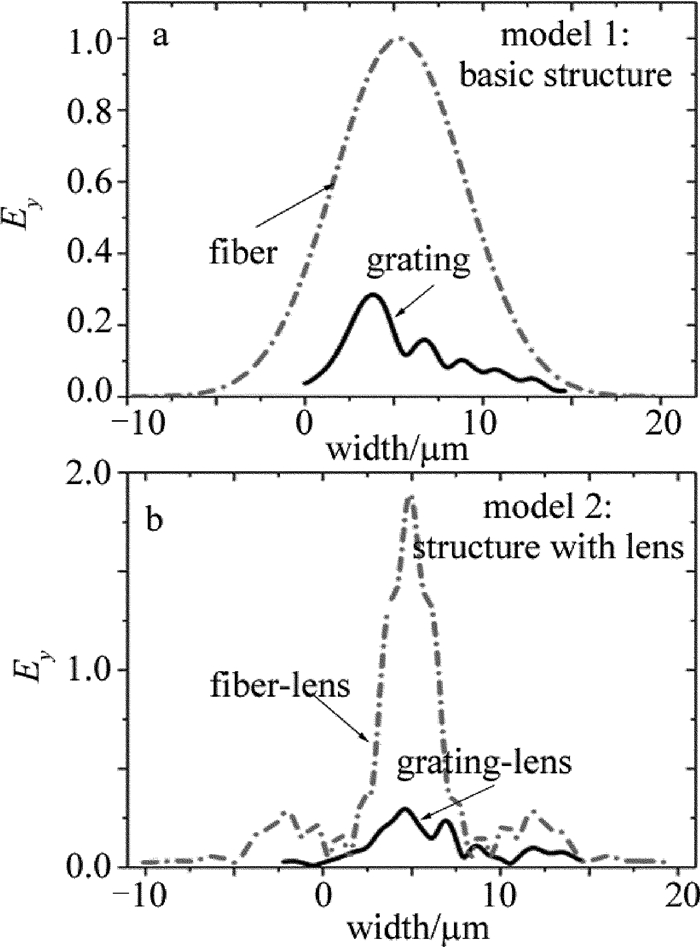
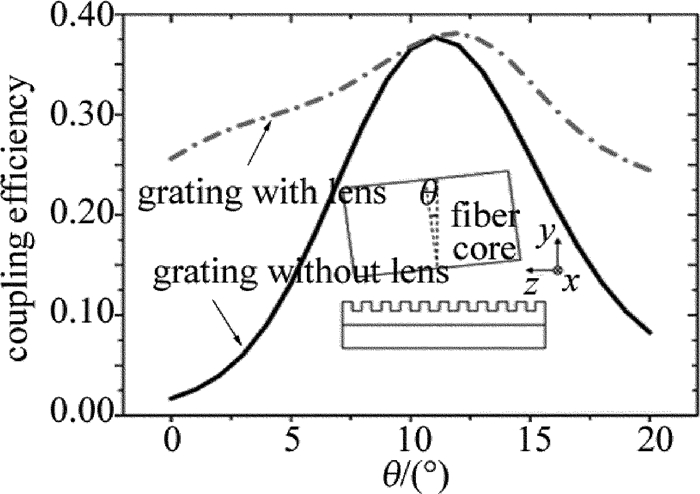
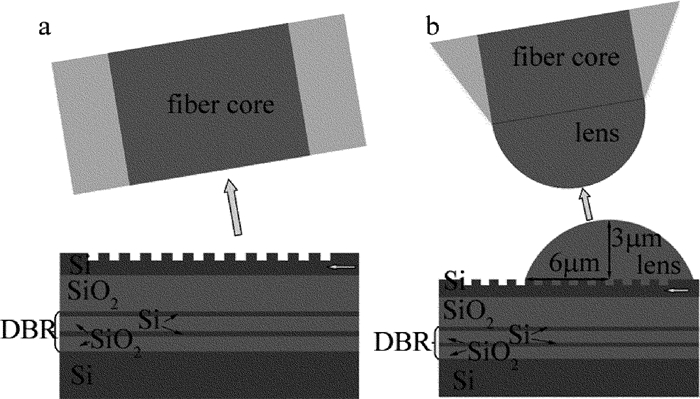
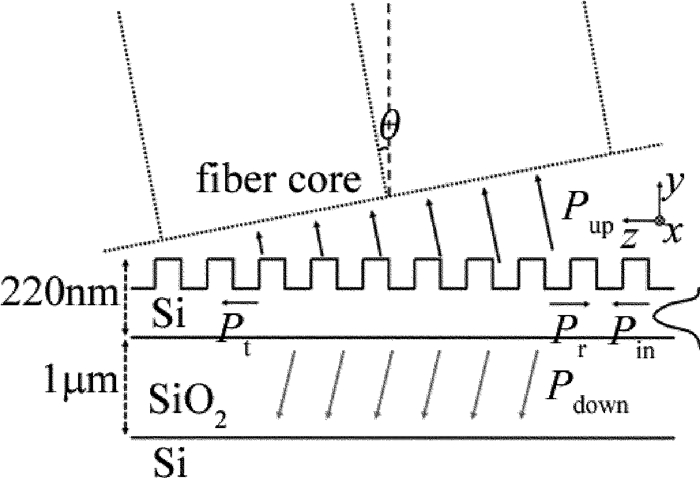
摘要: 为了提高硅基光栅耦合封装结构的耦合效率、增大容差范围，对光栅耦合的结构特性进行了理论分析，并采用时域有限差分法完成了仿真验证，在不改变光栅参量的基础上，对光栅耦合封装结构进行了改进，仿真建立了一款光栅上方和光纤端面分别增加透镜的优化结构，研究了影响耦合效率的因素。结果表明，增加透镜后，耦合效率有所增加，角度容差和带宽都有一定的优化；在衬底增加反射镜后，对波长1550nm的光耦合效率提高至73.809%。该研究结果可为光栅耦合的封装结构设计提供参考依据。Abstract: In order to improve the coupling efficiency and increase the tolerance range of grating coupling packaging structure on silicon substrate, the characteristics of grating coupling structure were analyzed theoretically and verified by simulation based on finite-difference time-domain method. After studying the main influence factors of the coupling efficiency, the basic grating coupling structure was improved without changing the parameters of the grating. A grating coupling structure with lenses was proposed. The results show that, after the lenses are added, coupling efficiency, angle tolerance and bandwidth are optimized through simulation. The coupling efficiency is increased to 73.809% with an incident wavelength in 1550nm when adding the reflectors on the substrate. The analysis results provide a reference for the design of the packaging structure of the grating coupling.
-
Keywords:
- gratings /
- packaging structure /
- finite-difference time-domain method /
- coupling efficiency /
- lens
-
-
![]()
Figure 5. Comparison of two grating coupling structures
a—model 1:basic structure b—model 2: structure with lens
![]()
Figure 7. Relationship between coupling efficiency and tolerance angle of model 1 and model 2
![]()
Figure 8. Relationship between coupling efficiency and wavelength of model 1 and model 2
![]()
Figure 9. Comparison of two grating coupling structures
a—model 3:basic structure+DBR b—model 4:structure with lens+DBR
![]()
Figure 10. Relationship between coupling efficiency and tolerance angle of model 3 and model 4
![]()
Figure 11. Relationship between coupling efficiency and wavelength of model 3 and model 4
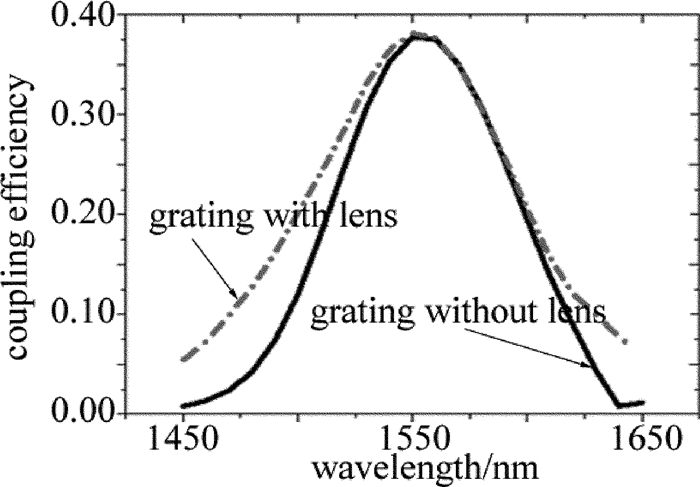
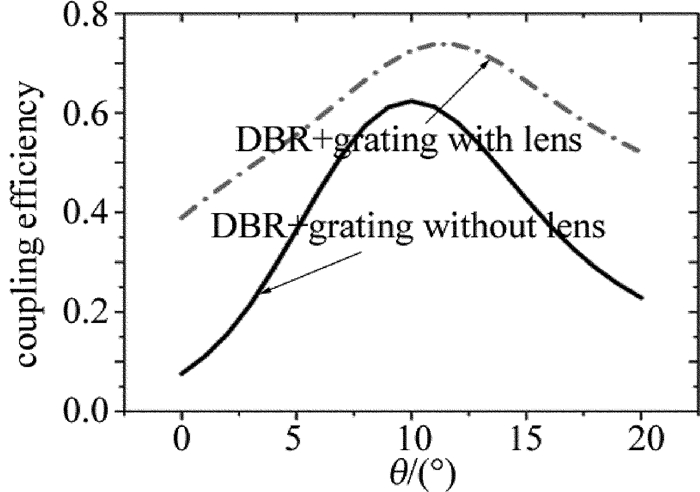
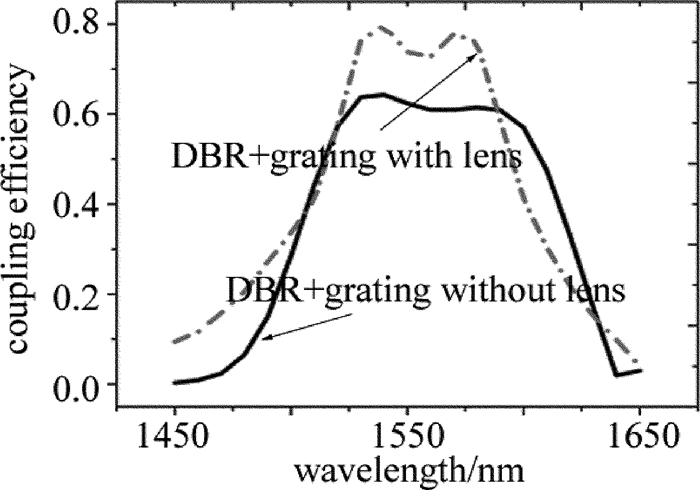
Table 1 Optimal angle and coupling efficiency of different grating coupling structures at working wavelength of 1550nm
model comments best angle/
(°)best coupling efficiency/% 1 grating without lenses(basic structure) 11 37.729 2 grating with lenses 12 38.126 3 grating without lenses + DBR 10 62.365 4 grating with lenses + DBR 11 73.809 
下载: 导出CSV
-
[1] KRISHNAMOORTHY A V, HO R, ZHENG X, et al.Computer systems based on silicon photonic interconnects[J]. Proceedings of the IEEE, 2009, 97(7): 1337-1361. DOI: 10.1109/JPROC.2009.2020712
[2] MILLER D A B. Rationale and challenges for optical interconnects to electronic chips[J]. Proceedings of the IEEE, 2000, 88(6): 728-749. DOI: 10.1109/5.867687
[3] JALALI B, FATHPOUR S. Silicon photonics[J]. Journal of Lightwave Technology, 2006, 24(12): 4600-4615. DOI: 10.1109/JLT.2006.885782
[4] MILLER D A B. Physical reasons for optical interconnection[J]. Optoelectron, 1997, 11(3):155-168.
[5] YANG B, LI Zh Y, XIAO X, et al. The progress of silicon-based grating couplers[J]. Acta Physica Sinica, 2013, 62(18): 184214(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/wlxb201318037
[6] BOLTEN J, HOFRICHTER J, MOLL N, et al. CMOS compatible cost-efficient fabrication of SOI grating couplers[J]. Microelectron Engineering, 2009, 86(4/6):1114-1116. http://dl.acm.org/citation.cfm?id=1540654.1540702
[7] LAERE F V, ROELKENS G, AYRE M, et al. Compact and highly efficient grating couplers between optical fiber and nanophotonicwaveguides [J]. Journal of Lightwave Technology, 2007, 25(1): 151-156. DOI: 10.1109/JLT.2006.888164
[8] BERND S, PETROV A, EICH M. Optimized grating coupler with fully etched slots[J]. Optics Express, 2009, 17(13):11066-11076. http://www.ncbi.nlm.nih.gov/pubmed/19550506
[9] LI C, ZHANG H, YU M, et al.CMOS-compatible high efficiency double-etched apodized waveguide grating coupler[J].Optics Express, 2013, 21(7):7868-7874. DOI: 10.1364/OE.21.007868
[10] LI C, CHEE K S, TAO J, et al.Silicon photonics packaging with lateral fiber coupling to apodized grating coupler embedded circuit[J]. Optics Express, 2014, 22(20):24235-24240. DOI: 10.1364/OE.22.024235
[11] TAILLAERT D, LAERE F V, AYRE M. Grating couplers for coupling between optical fibers and nanophotonicwaveguides[J]. Japanese Journal of Applied Physics, 2006, 45(45):6071-6077. http://adsabs.harvard.edu/abs/2006jajap..45.6071t
[12] TAILLAERT D, BIENSTMAN P, BAETS R. Compact efficient broadban grating coupler for silicon-on-insulator waveguides[J].Optics Letters, 2004, 29(23):2749-2751. DOI: 10.1364/OL.29.002749
[13] ROELKENS G, VERMEULEN D, SELVARAJA S, et al. Grating-based optical fiber interfaces for silicon-on-insulator photonic integrated circuits[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2011, 17(3):571-580. DOI: 10.1109/JSTQE.2010.2069087
[14] VERMEULEN D, SELVARAJA S, VERHEYEN P, et al. High-efficiency fiber-to-chip grating couplers realized using an advanced CMOS-compatible Silicon-On-Insulator platform[J]. Optics Express, 2010, 18(17):18278-18283. DOI: 10.1364/OE.18.018278
[15] OROBTCHOUK R, LAYADI A, GUALOUS H, et al. High-efficiency light coupling in a submicrometricsilicon-on-insulator waveguide[J].Applied Optics, 2000, 39(31):5773-5777. DOI: 10.1364/AO.39.005773
[16] YEE K S, CHEN J S. The finite-difference time-domain(FDTD) and the finite-volume time-domain(FVTD) methods in solving Maxwell's equations[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3):354-363. DOI: 10.1109/8.558651
[17] BIENSTMAN P, DERUDDER H, BESTS R, et al. Analysis of cylindrical waveguide discontinuities using vectorialeigenmodes and perfectly matched layers[J]. IEEE Transaction on Microwave Theory and Techniques, 2001, 49(2):349-354. DOI: 10.1109/22.903096
[18] FAN Sh W, ZHOU Q H. Analysis of diffraction characteristics of blazed gratings[J]. Laser Technology, 2010, 34(1):41-44 (in Chinese). http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201712005
[19] CHOU B C, VIS W, KHAN B, et al. Design and demonstration of micro-mirrors and lenses for low loss and low cost single-mode fiber coupling in 3-D glass photonic interposers[C]// IEEE Electronic Components & Technology Conference. New York, USA: IEEE, 2016: 497-503.
[20] LU W L, ZHENG Y, ZHAO W L, et al. Analysis coupling between a laser and a single-mode fiber with a ball lens based on Monte Carlo method[J]. Laser Technology, 2012, 36(3):338-341(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201203014.htm
[21] URA S, MURATA S, AWATSUJI Y, et al. Design of resonance grating coupler[J].Optics Express, 2008, 16(16):12207-12213. DOI: 10.1364/OE.16.012207
[22] SHEPPARD C J R. Approximate calculation of the reflection coefficient from a stratified medium[J]. Pure & Applied Optics Journal of the European Optical Society, 1995, A4(5):665-669. http://www.ingentaconnect.com/content/iop/pao/1995/00000004/00000005/art00018
-
期刊类型引用(6)
1. 杨伟业. 方形织构对压裂泵柱塞密封橡胶摩擦学性能研究. 装备制造技术. 2023(10): 56-59 . 
百度学术
2. 莫丽，贾杜平，何军，王国荣. 考虑橡胶弹性变形及织构直径对压裂泵柱塞密封摩擦学性能研究. 机械设计与研究. 2019(02): 91-95+100 . 百度学术
3. 刘衍聪，张本华，束宁凯，高喜龙，尹晓丽，金延朝. 激光表面织构对磨角度对40Cr干摩擦特性的影响. 应用激光. 2019(06): 941-948 . 百度学术
4. 王振，王兆强，罗一平，胡山，杨俭. 混合排列织构化滑动轴承承载力数值研究. 轻工机械. 2018(01): 35-40 . 百度学术
5. 符永宏，李进，符昊，张航成，潘彩云. 45~#钢光纤激光毛化数值模拟及实验研究. 激光技术. 2017(06): 909-915 . 本站查看
6. 刘强，林乃明，邹娇娟，谢瑞珍，王振霞，马永，王志华，唐宾. 改善钢铁材料摩擦学行为的表面织构研究现状. 表面技术. 2016(05): 41-50 . 百度学术
其他类型引用(18)
计量
- 文章访问数: 7
- HTML全文浏览量: 2
- PDF下载量: 2
- 被引次数: 24