Experimental study about improving the quality of in-focus image by means of optical scanning holography
-
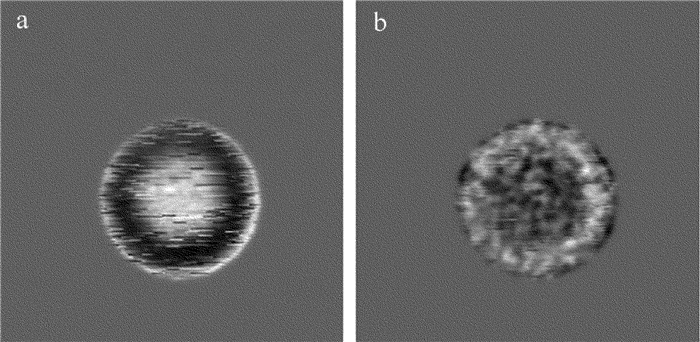
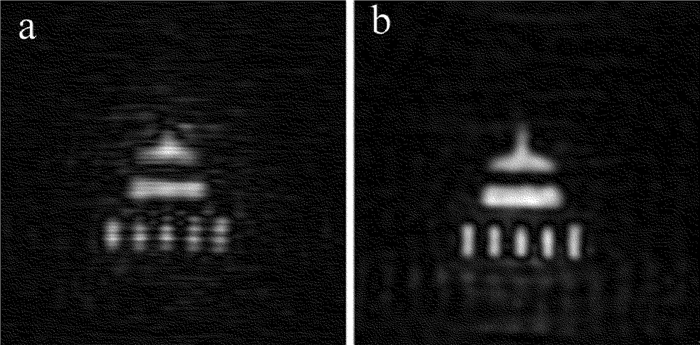
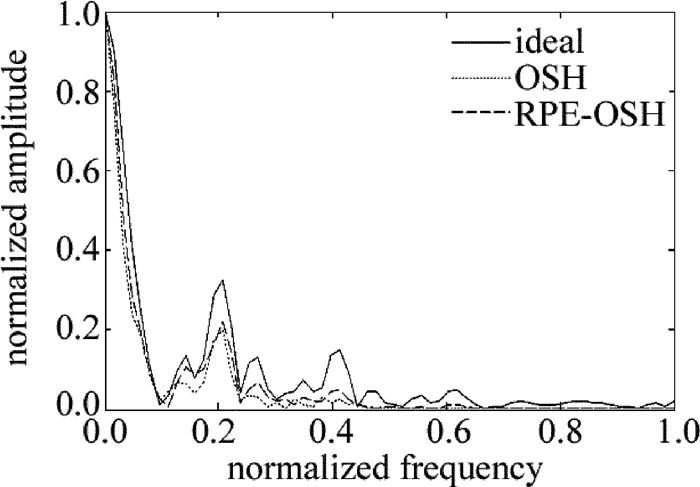
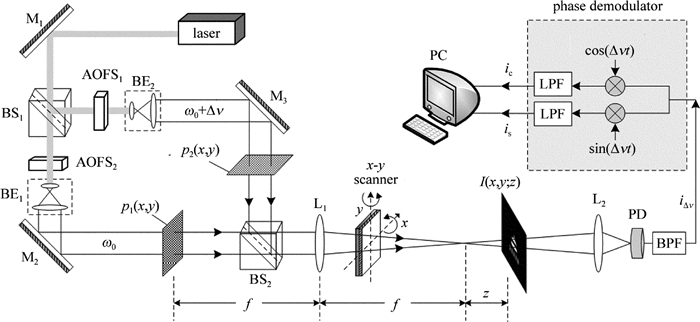
摘要: 为了改善光学扫描全息系统聚焦层重建图像的效果，采用随机相位光瞳替代传统针孔光瞳的方法，进行了理论的分析和实验验证，分别得到了传统光学扫描全息和基于随机相位编码的光学扫描全息系统下重建图像和原图像之间的信噪比、相关系数以及频谱分布比较结果。结果表明，在实验条件相同的情况下，基于随机相位编码的光学扫描全息系统重建的图像具有更高的信噪比和相关系数，且其图像频谱和原图像频谱曲线的变化趋势更相似，因而更接近于原图像。Abstract: In order to improve the quality of in-focus reconstructed images, random phase pupil was used to replace the pinhole in optical scanning holography system. After theoretical analysis and experimental verification, the comparison of signal to noise ratio, correlation coefficient and frequency spectrum distribution between the original and reconstructed images in the optical scanning holography system and the system based on random phase pupil was gotten respectively. The results show that under the same experimental condition, the reconstructed image from optical scanning holography based on random phase encoding has higher signal-to-noise ratio and correlation coefficient. The change trend of the reconstructed image spectrum is similar to that of the original image.
-
-
![]()
Figure 7. Relationship between amplitude and frequency of the original image and the reconstructed image
-
[1] DUNCAN B D, POON T C. Gaussian beam analysis of optical scanning holography[J]. Journal of the Optical Society of America, 1992, A9(2): 229-236. DOI: 10.1364-JOSAA.9.000229/
[2] LAM E Y, ZHANG X, VO H, et al. Three-dimensional microscopy and sectional image reconstruction using optical scanning holography[J]. Applied Optics, 2009, 48(34): 113-119. DOI: 10.1364/AO.48.00H113
[3] POON T C, KIM T. Optical image recognition of three-dimensional objects[J]. Applied Optics, 1999, 38(2): 370-381. DOI: 10.1364/AO.38.000370
[4] KIM T, POON T C, INDEBETOUW G. Depth detection and image recovery in remote sensing by optical scanning holography[J]. Optical Engineering, 2002, 41(6): 1331-1338. DOI: 10.1117/1.1476939
[5] POON T C. Three-dimensional television using optical scanning holography[J]. Journal of Information Display, 2002, 3(3): 12-16. DOI: 10.1080/15980316.2002.9651895
[6] POON T C, KIM T, DOH K. Optical scanning cryptography for secure wireless transmission[J]. Applied Optics, 2003, 42(32): 6496-6503. DOI: 10.1364/AO.42.006496
[7] LIN Ch, SHEN X J, DU Sh, et al. Characteristic analysis of encryption and decryption in random polarization optical encryption algorithm[J].Laser Technology, 2014, 38(4):515-521(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201404016
[8] KE J, POON T C, LAM E Y. Depth resolution enhancement in optical scanning holography with a dual-wavelength laser source[J]. Applied Optics, 2011, 50(34): 285-296. DOI: 10.1364/AO.50.00H285
[9] INDEBETOUW G, TADA Y, ROSEN J, et al. Scanning holographic microscopy with resolution exceeding the Rayleigh limit of the objective by superposition of off-axis holograms[J]. Applied Optics, 2007, 46(6): 993-1000. DOI: 10.1364/AO.46.000993
[10] KATZ B, ROSEN J. Super-resolution in incoherent optical imaging using synthetic aperture with Fresnel elements[J]. Optics Express, 2010, 18(2): 962-972. DOI: 10.1364/OE.18.000962
[11] LINFOOT E H, WOLF E. Diffraction images in systems with an annular aperture[J]. Proceedings of the Physical Society, 1953, B66(2): 145-149. http://adsabs.harvard.edu/abs/1953PPSB...66..145L
[12] ZHOU X, DOBSON K, SHINODA Y, et al. Sectional image reconstruction in optical scanning holography using a random-phase pupil[J]. Optics Letters, 2010, 35(17): 2934-2936. DOI: 10.1364/OL.35.002934
[13] WANG Y, HU J P, YUAN S, et al. Analysis on the lateral resolution of optical scanning holography system based on random phase encoding using restricted pupils[J]. Journal of Modern Optics, 2014, 61(9): 721-727. DOI: 10.1080/09500340.2014.909957
[14] JIANG Y F, ZHOU X, WANG Y, et al. Optical scanning holography based on a binary phase pupil[J]. Laser Technology, 2013, 37(6):723-727(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201306004
[15] POON T C. Optical scanning holography with MATLAB[M]. New York, USA: Springer, 2007:65-96.
[16] WANG Y. Analysis on the lateral resolution of optical scanning holography system based on random phase encoding[D]. Chengdu: Sichuan University, 2014: 39-47(in Chinese).
-
期刊类型引用(4)
1. 曾胜财，甘亮勤. 编码法制彩色动态全息. 激光技术. 2021(02): 229-232 . 
本站查看
2. 李凯勇. 机器学习的光照不均图像边缘检测系统. 激光杂志. 2021(03): 130-134 . 百度学术
3. 于琳琳. 基于激光全息技术的漆画无损修复研究. 激光杂志. 2021(12): 207-211 . 百度学术
4. 张源峰，程恩. 光学图像信息多标记特征分层识别系统设计. 激光杂志. 2020(07): 209-212 . 百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 3
- HTML全文浏览量: 0
- PDF下载量: 7
- 被引次数: 4