Mid-infrared field phase measurement and attosecond pulse generation
-
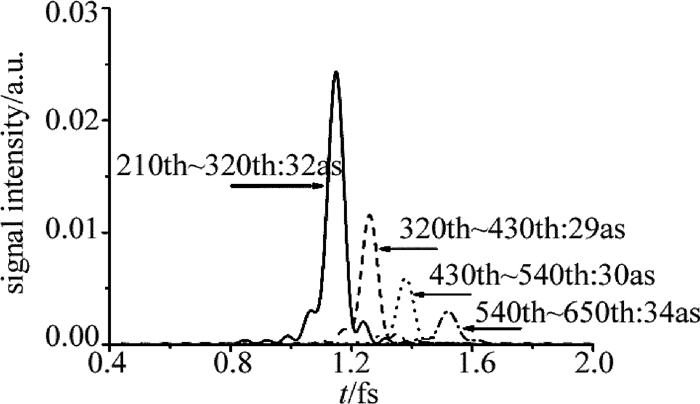
摘要: 为了测量中红外激光相位及获得阿秒脉冲，采用高次谐波截止能量随激光相位改变而变化的方法，进行了中红外激光相位测量及阿秒脉冲输出的研究。引入一束少周期激光场后，组合场相位对谐波发射截止能量的影响要比单独中红外激光场相位对谐波截止能量的影响明显很多。因此，提出了一种利用谐波截止能量与相位角的对应关系测量多周期中红外激光相位的方法。同时理论研究了3束中红外激光场下发射高次谐波及阿秒脉冲的特点。结果表明，适当调节3束激光场的延迟时间和相位角，不仅谐波发射的截止能量得到了延伸，而且单一的量子路径也被选择出来对谐波发射起作用，形成了一个272eV的平台区；通过叠加谐波谱上的谐波，可获得一系列脉宽为34as的X射线光源。该研究对中红外激光相位测量及阿秒脉冲的输出是有帮助的。Abstract: In order to measure the phase of mid-infrared field and to obtain the attosecond pulse, the investigation on mid-infrared field phase measurement and attosecond pulse generation has been presented by using the relationship between phase and harmonic cutoff energy. With the introduction of a few-cycle pulse to mid-infrared field, the effect of phase of the combined field on harmonic cutoff energy became much more distinct in comparison with the single field. One new method of phase measurement was gotten. Further, harmonic extension spectra and attosecond pulse generation of the three-color mid-infrared field were numerically investigated. The results show that by properly adjusting the delay times and phases of three pulses, not only harmonic cutoff energy is extended, but also single quantum path is selected to contribute to the harmonic generation, resulting in supercontinuum with bandwidth of 272eV. Finally, by superposing the properly selected harmonics in supercontinuum region, a series of X-ray pulses with pulsewidth of 34as can be obtained. The investigation is helpful for phase measurement of mid-infrared field and attosecond pulse generation.
-
-
![]()
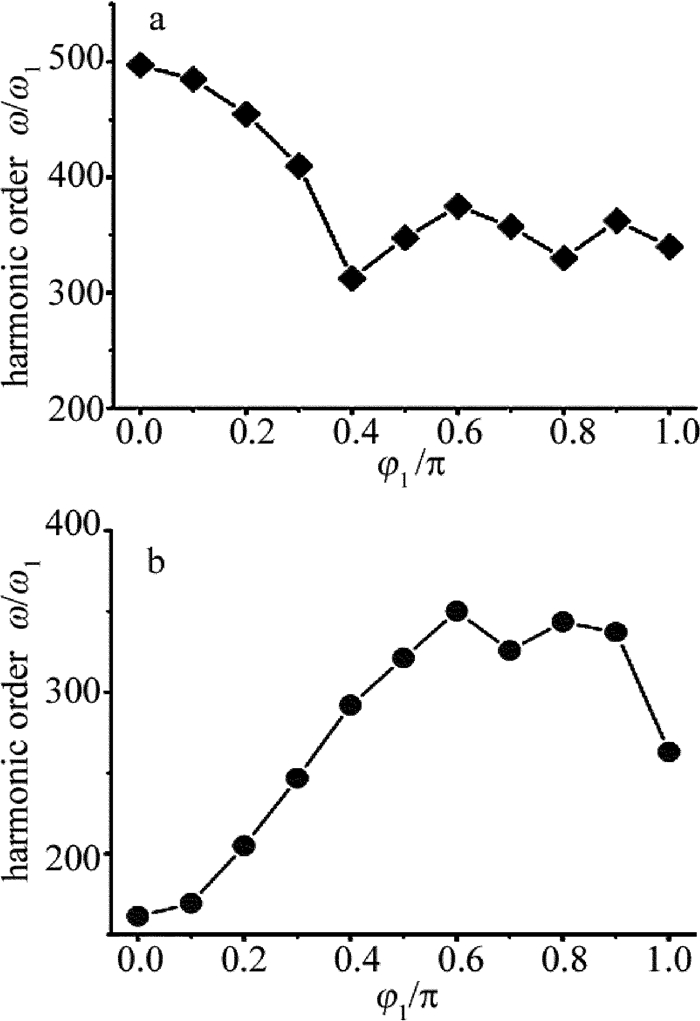
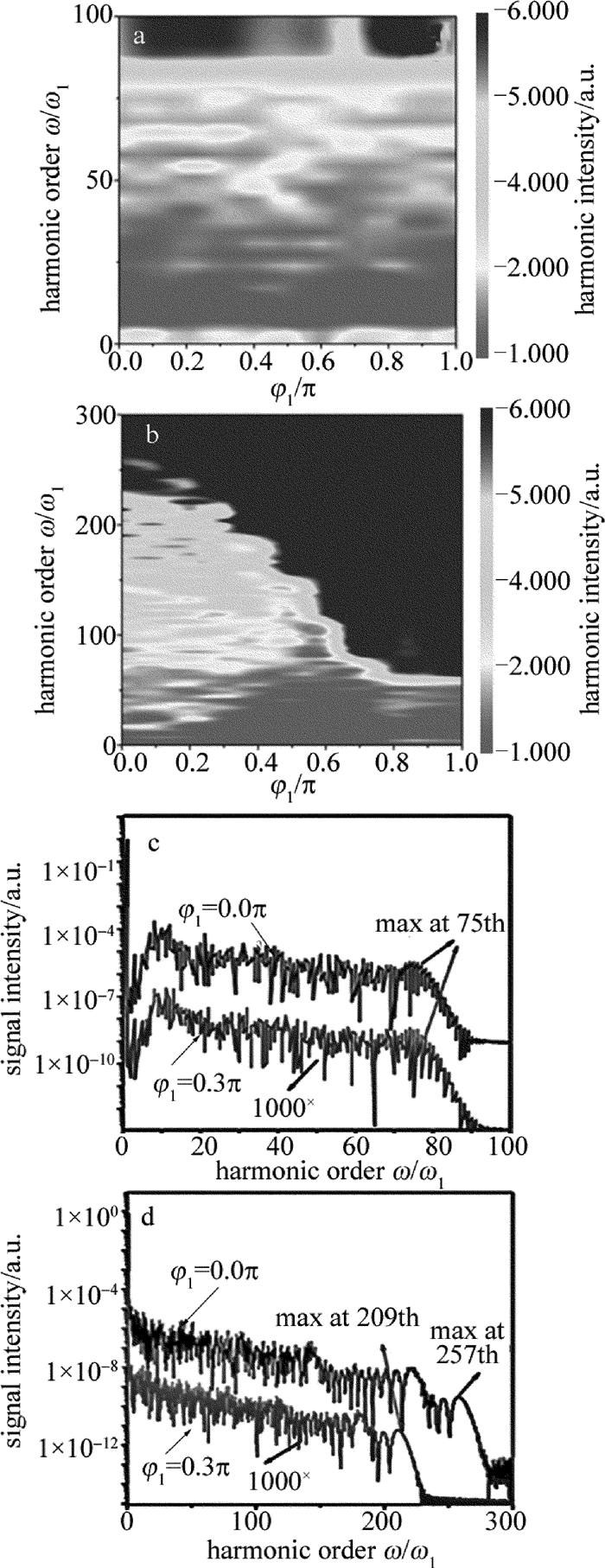
Figure 1. a—relationship between harmonic order ω/ω1 and phase angle φ1 of the single field (20fs/800nm) b—relationship between harmonic order ω/ω1 and phase angle φ1 of the combined field (20fs/800nm+5fs/800nm) c—relationship between signal intensity and harmonic order ω/ω1 of the single field (20fs/800nm) d—relationship between signal intensity and harmonic order ω/ω1 of the combined field (20fs/800nm+5fs/800nm)
![]()
Figure 2. a—relationship between E(t) and t of the single field (20fs/800nm) b—kinetic energies on ionization and recombination of the single field (20fs/800nm) from A to B c—kinetic energies on ionization and recombination of the single field (20fs/800nm) from B to C d—relationship between E(t) and t of the combined field (20fs/800nm+5fs/800nm) e—kinetic energies on ionization and recombination of the combined field (20fs/800nm+5fs/800nm) from A to B f—kinetic energies on ionization and recombination of the combined field (20fs/800nm+5fs/800nm) from B to C
![]()
Figure 3. Relationship between harmonic order ω/ω1 and t
a—the single field (20fs/800nm), φ1=0.0π b—the single field (20fs/800nm), φ1=0.3π c—the combined field (20fs/800nm+5fs/800nm), φ1=0.0π, φ2=0.0π d—the combined field (20fs/800nm+5fs/800nm), φ1=0.3π, φ2=0.0π
![]()
Figure 4. Relationship between harmonic order ω/ω1 and phase angle φ1
a—the single field (20fs/2000nm) b—the combined field (20fs/2000nm+5fs/800nm)
![]()
Figure 5. Relationship between harmonic order ω/ω1 and phase angle φ1 of the combined field (20fs/2000nm+5fs/800nm)
a—τ12=0.0π, φ2=0.0π, I2=7.0×1014W/cm2 b—τ12=0.25π, φ2=0.5π, I2=5.0×1014W/cm2
![]()
Figure 6. Relationship driven by the three-color field (20fs/2000nm+5fs/800nm+20fs/800nm~2000nm)
a—between signal intensity and harmonic order ω/ω1 b—between E(t) and t when λ3=1200nm and λ3=2000nm c—between harmonic order ω/ω1 and t when λ3=1200nm d—between harmonic order ω/ω1 and t when λ3=2000nm
![]()
Figure 7. Relationship between signal intensity and harmonic order ω/ω1 driven by the three-color field (20fs/2000nm+5fs/800nm+20fs/1200nm)
a—with different φ1 b—with different φ2 c—with different φ3 d—with different φ1, φ2 and φ3
![]()
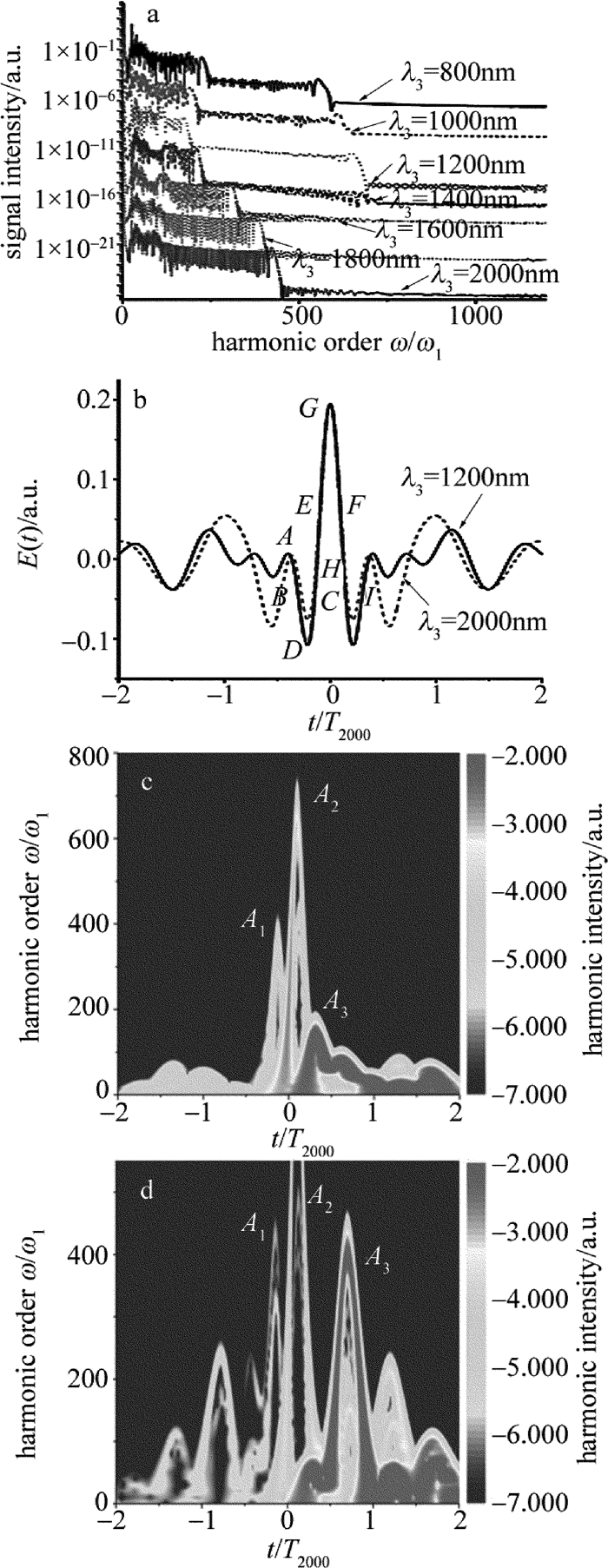
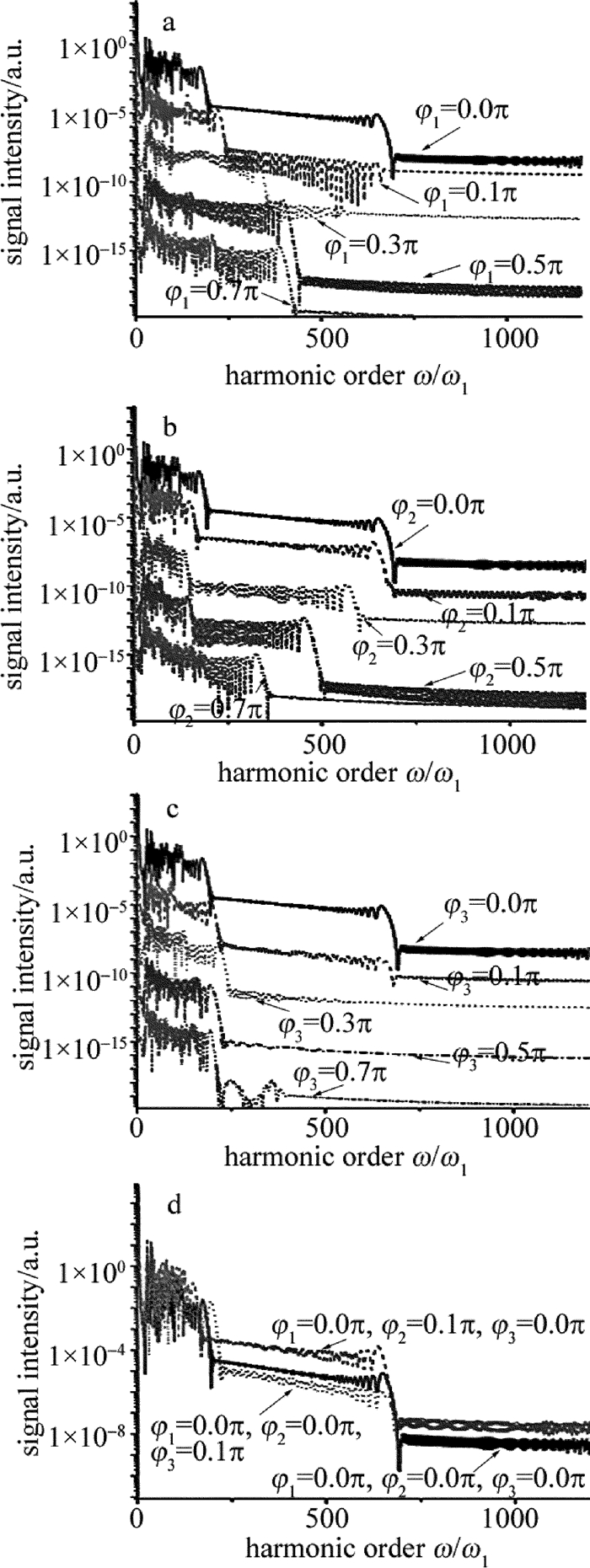
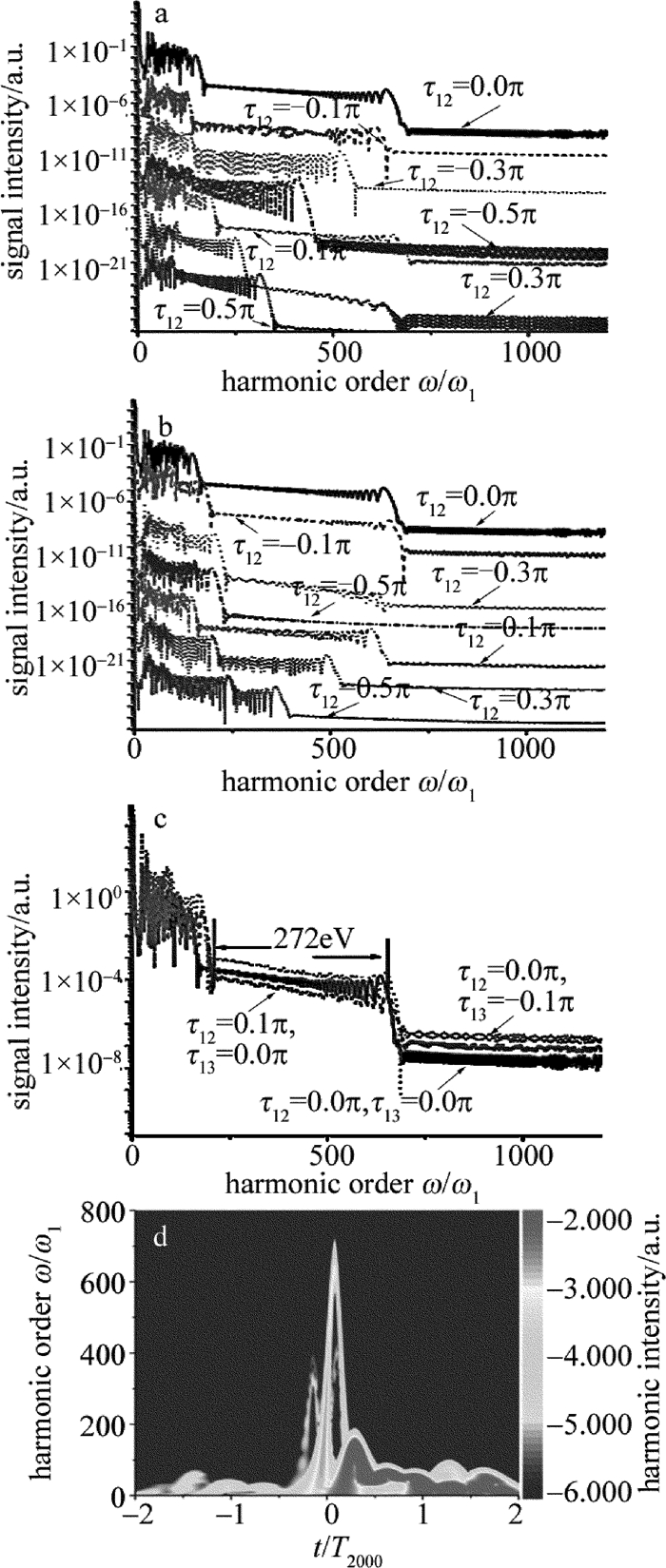
Figure 8. Relationship between signal intensity and harmonic order ω/ω1 driven by the three-color field(20fs/2000nm+5fs/800nm+20fs/1200nm)
a—with different τ12 b—with different τ13 c—with different τ12 and τ13) d—between harmonic order ω/ω1 and t driven by three-color laser field(20fs/2000nm+5fs/800nm+20fs/1200nm)
![]()
Figure 9. Temporal profiles of attosecond pulses by superposing the optimal three-color field(20fs/2000nm+5fs/800nm+20fs/1200nm, φ2=0.1π, τ12=0.0π, τ13=-0.1π)
Table 1 Relationship between phase angle φ1 and harmonic order ω/ω1 of the combined field (20fs/800nm+5fs/800nm) when τ12=0.0π, φ2=0.0π
φ1/π 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 harmonic order ω/ω1 257 250 238 209 179 141 105 75 59 54 50 
下载: 导出CSV
Table 2 Relationship between the maximum harmonic order ω/ω1 and phase angle φ1 of the combined field (20fs/2000nm+5fs/800nm) when τ12=0.0π, φ2=0.0π
φ1/π 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 harmonic order ω/ω1 403 384 330 293 264 287 300 295 316 309 305
下载: 导出CSV
-
[1] DRESCHER M, HENTSCHE M, KIENBERGER R, et al. Time-resolved atomic inner-shell spectroscopy[J].Nature, 2002, 419(6909):803-807. DOI: 10.1038/nature01143
[2] UIBERACKER M, UPHUES T, SCHULTZE M, et al. Attosecond real-time observation of electron tunnelling in atoms[J].Nature, 2007, 446(7136):627-632. DOI: 10.1038/nature05648
[3] HE F, RUIZ C, BECKER A. Control of electron excitation and localization in the dissociation of H2+ and its isotopes using two sequential ultrashort laser pulses[J].Physical Review Letters, 2007, 99(8):083002. DOI: 10.1103/PhysRevLett.99.083002
[4] SANSONE G, KELKENSBERG F, PEREZ-TORRES J F, et al. Electron localization following attosecond molecular photoionization[J]. Nature, 2010, 465(7299):763-U3. DOI: 10.1038/nature09084
[5] KLING M F, SIEDSCHLAG C, VERHOEF A J, et al. Control of electron localization in molecular dissociation[J].Science, 2006, 312(5771):246-248. DOI: 10.1126/science.1126259
[6] YUAN K J, BANDRAUK A D. Single circularly polarized attosecond pulse generation by intense few cycle elliptically polarized laser pulses and terahertz fields from molecular media[J].Physical Review Letters, 2013, 110(2):023003. DOI: 10.1103/PhysRevLett.110.023003
[7] GOULIELMAKIS E, SCHULTZE M, HOFSTETTER M, et al. Single-cycle nonlinear optics[J].Science, 2008, 320(5883):1614-1617. DOI: 10.1126/science.1157846
[8] WANG C, LIU H L, TIAN J S, et al. Analysis of intrinsic atomic phase in process of extreme ultraviolet attosecond pulse generation[J].Laser Technology, 2012, 36(3):342-345(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201203015.htm
[9] WANG C, KANG Y F, TIAN J S, et al. Analysis of phase dependence of the two single-attosecond-pulse generation techniques[J].Laser Technology, 2012, 36(4):516-519(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201204022.htm
[10] CORKUM P B. Plasma perspective on strong field multiphoton ionization[J].Physical Review Letters, 1993, 71(13):1994-1997. DOI: 10.1103/PhysRevLett.71.1994
[11] FENG L Q, CHU T S. High-order harmonics extension and isolated attosecond pulse generation in three-color field:Controlling factors[J].Physical Letters, 2011, A375(41):3641-3648. http://www.sciencedirect.com/science/article/pii/S0375960111010280
[12] LU R F, HE H X, GUO Y H, et al. Theoretical study of single attosecond pulse generation with a three-colour laser field[J].Journal of Physics, 2009, B42(22):225601. DOI: 10.1088-0953-4075-42-22-225601/
[13] ZENG Z N, CHENG Y, SONG X H, et al. Generation of an extreme ultraviolet supercontinuum in a two-color laser field[J]. Physical Review Letters, 2007, 98(20):203901. DOI: 10.1103/PhysRevLett.98.203901
[14] FENG L Q, CHU T S. Generation of an isolated sub-40-as pulse u-sing two-color laser pulses:Combined chirp effects[J].Physical Review, 2011, A84(5):053853. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=VIRT05000010000012000183000001&idtype=cvips&gifs=Yes
[15] FENG L Q, CHU T S. Nuclear signatures on the molecular harmonic emission and the attosecond pulse generation[J]. The Journal of Chemical Physics, 2012, 136(5):054102. DOI: 10.1063/1.3681165
[16] LI P C, ZHOU X X, WANG G L, et al. Isolated sub-30-as pulse generation of an He+ ion by an intense few-cycle chirped laser and its high-order harmonic pulses[J].Physical Review, 2009, A80(5):053825. http://adsabs.harvard.edu/abs/2009PhRvA..80e3825L
[17] CHANG Z H. Chirp of the single attosecond pulse generated by a polarization gating[J].Physical Review, 2005, A71(2):023813. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PLRAAN000071000002023813000001&idtype=cvips&gifs=Yes
[18] DU H C, HU B T. Broadband supercontinuum generation method combining mid-infrared chirped-pulse modulation and generalized polarization gating[J].Optics Express, 2010, 18(25):25958-25966. DOI: 10.1364/OE.18.025958
[19] ZHANG Q B, LU P X, LAN P F, et al. Multi-cycle laser-driven broadband supercontinuum with a modulated polarization gating[J].Optics Express, 2008, 16(13):9795-9803. DOI: 10.1364/OE.16.009795
[20] CHOU Y, LI P C, HO T S, et al. Optimal control of high-order harmonics for the generation of an isolated ultrashort attosecond pulse with two-color midinfrared laser fields[J].Physical Review, 2015, A91(6):063408. DOI: 10.1103/PhysRevA.91.063408
[21] LI P C, LAUGHLIN C, CHU S I. Generation of isolated sub-20-attosecond pulses from He atoms by two-color midinfrared laser fields[J].Physical Review, 2014, A89(2):023431. DOI: 10.1103/PhysRevA.89.023431
[22] FENG L Q, LIU H. Generation of the ultrabroad bandwidth with keV by three-color low intense mid-infrared inhomogeneous pulse[J].Optics & Laser Technology, 2016, 81:7-13. http://www.sciencedirect.com/science/article/pii/S0030399215302991
[23] LU R F, ZHANG P Y, HAN K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields[J].Physical Review, 2008, E77(6):066701. DOI: 10.1103-PhysRevE.77.066701/
[24] FENG L Q, LIU H. Attosecond extreme ultraviolet generation in cluster by using spatially inhomogeneous field[J].Physics of Plasmas, 2015, 22(1):013107. DOI: 10.1063/1.4905861
[25] FENG L Q, DUAN Y B, CHU T S. Harmonic extension and attosecond pulse generation by using the modified three-color chirped pulse[J].Annalen der Physik, 2013, 525(12):915-920. DOI: 10.1002/andp.v525.12
[26] MIAO X Y, DU H N. Theoretical study of high-order-harmonic generation from asymmetric diatomic molecules[J].Physical Review, 2013, A87(5):053404. http://d.old.wanfangdata.com.cn/Conference/8690370
[27] HU J, HAN K L, HE G Z. Correlation quantum dynamics between an electron and D2+ molecule with attosecond resolution[J].Physical Review Letters, 2005, 95(12):123001. DOI: 10.1103/PhysRevLett.95.123001
[28] BURNETT K, REED V C, COOPER J, et al. Calculation of the background emitted during high-harmonic generation[J].Physical Review, 1992, A45(5):3347-3349. DOI: 10.1103-PhysRevA.45.3347/
[29] FENG L Q, CHU T S. High-order harmonic generation spectra and isolated attosecond pulse generation with a two-color time delayed pulse[J].Journal of Electron Spectroscopy and Related Phenomena, 2012, 185(1/2):39-46. http://www.sciencedirect.com/science/article/pii/S0368204811001289
[30] ANTOINE P, PIRAUX B, MAQUET A. Time profile of harmonics generated by a single atom in a strong electromagnetic field[J].Physical Review, 1995, A51(3):R1750-R1753. http://europepmc.org/abstract/MED/9911899
[31] MAIRESSE Y, BOHAN A D, FRASINSKI L J, et al. Attosecond synchronization of high-harmonic soft X-rays[J]. Science, 2003, 302(5650):1540-1543. DOI: 10.1126/science.1090277
计量
- 文章访问数: 5
- HTML全文浏览量: 0
- PDF下载量: 13