网站地图
-
随着视觉技术的进步，机器人视觉伺服有了较大的发展，视觉伺服应用于选择顺应性装配机器手臂(selective compliance assembly robot arm，SCARA)的研究备受关注。而高质量装配的前提是高精度的定位。当前决定机器人性能指标分别是：机器人的重复定位精度、系统的绝对定位精度。许多SCARA机器人本体重复定位精度为20μm左右，但系统的绝对定位精度一般为1mm~3mm。
SCARA机器人模型的不精准会影响其平面定位精度，而SCARA机器人1轴和2轴的强耦合串联机械结构与平面定位精度直接相关。现有提高SCARA机器人平面绝对定位精度方法也称为机器人标定。机器人标定可以分为机器人运动学标定[1-4]和机器人非运动学标定[5]。运动学标定一般分为4个步骤：建模、测量[6-8]、参量辨识和误差补偿[9]。传统的运动学标定侧重建立复杂的运动学模型并注重模型几何参量改变带来的影响。对运动学标定的误差补偿关注较少，误差补偿即当辨识出运动学参量后，需要附加一定的控制算法或者修改机器人原有的控制系统参量来提高机器人的绝对定位精度。传统误差补偿方法可以分为如下几类：基于神经网络补偿法、基于插补思想补偿法、微分误差补偿法、关节空间补偿法。
参考文献[10]中提出基于空间网格的机器人精度补偿方法，通过空间插补方式对目标期望点定位预测，但最小空间网格划分的精度会直接影响补偿的效果。参考文献[11]中基于分析空间网格相邻两点之间内在关联，提出了定位误差相似度的概念，采用反距离加权法进行插值优化网格步长，但未考虑温度发生变化时带来的误差。参考文献[12]中基于空间网格精度补偿的基础，采用粒子群优化神经网络的机器人精度补偿方法，降低环境因素变化对补偿效果的影响，但训练神经网络的采样样本数量偏大。参考文献[13]中提出基于模型控制方法和智能计算相结合的方法，以面向小样本原理的支持向量机回归算法预测位置误差, 有利于减少位姿测量的点数，但基于小样本原理构建的模型应用范围有一定的限制。参考文献[14]中提出基于距离误差的机器人误差补偿模型，避免了测量系统坐标系与机器人基础坐标系之间的转换误差，但模型的建立需要测量几何参量的微小偏差，对仪器的精度要求较高。参考文献[15]中提出基于网格线自主定位系统，通过采集加速度与角速度信息计算移动偏差来提高定位精度，但此方法受限于传感器的本身精度。
针对以上问题，本文中提出一种新的机器人精确定位补偿方法，该方法运用基于网格模型原理结合最小距离误差逼近原则提高SCARA机器平面绝对定位精度，并将补偿效果与数据进行了细化的分析，发现此方法很大程度上弥补了因模型不精准而造成的平面定位精度不高的现象。
-
SCARA机器人的系统定位精度直观上表现为1轴和2轴平面定位精度与3轴确定的垂直定位精度的总和。SCARA机器人的1轴和2轴具有强耦合性，3轴和4轴分别确定机器人的垂直定位精度和旋转定位精度。在分析机器人的平面定位精度补偿时，只需考虑1轴和2轴的共同作用。SCARA机器人机械结构如图 1所示。图中θi(i=1, 2, 3, 4)代表SCARA机器人第i轴的旋转角度; l1, l2代表决定SCARA机器人平面定位的第1轴和第2轴的轴长; ri(i=1, 2, 3, 4)代表SCARA机器人的每个轴的坐标系。
Figure 1. Mechanical structure of SCARA
SCARA机器人在平面上的定位取决于1轴θ1、2轴θ2的共同作用，定位精度的控制量是关节角度(θ1, θ2):
$ {\theta _1} = m{\Delta _1},{\theta _2} = n{\Delta _2} $
(1) 式中, m, n为系数，Δ1, Δ2为电机1、电机2的指令单位关节度数。SCARA机器人平面定位简化模型如图 2所示。
Figure 2. Model diagram of SCARA robot
SCARA机器人通过视觉传感器得到期望点的笛卡尔空间坐标，通过运动学正解求得关节空间角度:
$ \left( {x,y} \right) = f\left( {{\theta _1},{\theta _2}} \right) $
(2) 同样易知：
$ {\left( {{\rm{d}}x,{\rm{d}}y} \right)^{\rm{T}}} = \mathit{\boldsymbol{J}}\left[ {{\theta _1},{\theta _2}} \right] \times {\left[ {{\rm{d}}{\theta _1},{\rm{d}}{\theta _2}} \right]^{\rm{T}}} $
(3) 式中, J是雅克比矩阵。
由图 2可知, SCARA机器人正运动学的表达式为：
$ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_1}\cos {\theta _1} + {l_2}\cos \left( {{\theta _1} + {\theta _2}} \right)}\\ {{l_1}\sin {\theta _1} + {l_2}\sin \left( {{\theta _1} + {\theta _2}} \right)} \end{array}} \right] $
(4) 且由：
$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\rm{d}}x}\\ {{\rm{d}}y} \end{array}} \right] = \mathit{\boldsymbol{J}} \cdot \left[ {{\rm{d}}\theta } \right] = }\\ {\left[ {\begin{array}{*{20}{c}} { - {l_1}\sin {\theta _1} - {l_2}\sin \left( {{\theta _1} + {\theta _2}} \right)}&{ - {l_2}\sin \left( {{\theta _1} + {\theta _2}} \right)}\\ {{l_1}\cos {\theta _1} + {l_2}\cos \left( {{\theta _2} + {\theta _2}} \right)}&{{l_2}\cos \left( {{\theta _1} + {\theta _2}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{d}}{\theta _1}}\\ {{\rm{d}}{\theta _2}} \end{array}} \right]} \end{array} $
(5) 对比(3)式、(5)式得到雅克比矩阵:
$ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{l_1}\sin {\theta _1}{l_2}\sin \left( {{\theta _1} + {\theta _2}} \right)}&{{l_2}\sin \left( {{\theta _1} + {\theta _2}} \right)}\\ {{l_1}\cos {\theta _1} + {l_2}\cos \left( {{\theta _2} + {\theta _2}} \right)}&{{l_2}\cos \left( {{\theta _1} + {\theta _2}} \right)} \end{array}} \right] $
(6) -
传统的网格模型构建把机器人末端工作区域按照指定步长划分成正交网格线组成的平面。网格的构建并没有考虑电机的运动特性，在微小距离的驱动过程中不能明确电机的移动增量, 且平面的定位精度与设定的网格步长紧密相关。改进后的网格模型从机器人关节空间构建模型，由粒度点、重复定位精度、电机指令单位关节度数三部分组成。网格模型有4个粒度点，每个粒度点代表机器人末端关节空间位置点，即网格的每个端点是真正意义上可达的。由于重复定位精度的影响，机器人重复多次到达同一个粒度点，多次到达的实际点分布情况会形成以粒度点为圆心的一个近似圆，圆的半径为重复定位精度。每个粒度点之间关节空间的间距分别是kΔ1或kΔ2，k是一个可以设定的整数(k=1, 2, …, n)。且每个设置的粒度点同时也是以此SCARA机器人的重复定位精度为半径的近似圆的圆心点，其网格模型结构如图 3所示。图 3中Ei代表机器人末端进入到的圆形区域范围，Pi代表设置的粒度点，Di代表Ei的半径，Di的大小为机器人的重复定位精度, 1≤i≤4，Ω是由P1, P2, P3 3点确定的外接圆圆心，P0是期望点, S1代表粒度点P1运动到点的方向矢量; S2代表粒度点P2运动到P4点的方向矢量。
Figure 3. Structure of grid model
根据(5)式可知：
$ {\mathit{\boldsymbol{S}}_1} = \mathit{\boldsymbol{J}}\left( {{P_0}} \right) \times {\left[ {k{\Delta _1},0} \right]^{\rm{T}}} $
(7) $ {\mathit{\boldsymbol{S}}_2} = \mathit{\boldsymbol{J}}\left( {{P_0}} \right) \times {\left[ {0,k{\Delta _2}} \right]^{\rm{T}}} $
(8) 通过视觉传感器得到期望点图像坐标，由坐标变换得到期望点的笛卡尔坐标P0(x0, y0)，再通过相应的坐标变换得到期望点的关节空间坐标P0(θ1, 0, θ2, 0)，驱动机器人前往期望点，分析机器人末端第1次到达的实际位置点P1(x0′, y0′)与期望点P0(x0, y0)位置的距离偏差，构建改进后的起始网格模型，使期望点处于构建的网格模型区域内，各粒度点的关节空间位置分别为：P1(θ1, θ2)简写为P1; P2(θ1+kΔ1, θ2)简写为P2; P3(θ1, θ2+kΔ2)简写为P3; P4(θ1+kΔ1, θ2+kΔ2)简写为P4。
由于模型粒度点在关节空间之间间距分别是kΔ1或kΔ2，这样构建的网格模型在关节空间中呈现的是一个矩形形状。而在笛卡尔空间中呈现的是一个近似矩形的平行四边形。
驱动机器人第1次运动指令的关节度数为P0(θ1, 0, θ2, 0)，由于相机坐标与机器人坐标转换过程中的误差累计，实际机器人的末端位置P1(x0′, y0′)与期望点P0(x0, y0)有距离偏差，但是P1(x0′, y0′)的关节空间坐标位置P1(θ1, θ2)就是P0(x0, y0)推导出的关节控制位置P0(θ1, 0, θ2, 0)，因此把P1(θ1, θ2)设定为网格模型的起始点。
机器人运动到起始目标关节位置后，计算各设定的粒度点与期望点距离误差，选择距离误差最小值的粒度点作为驱动机器人从起始目标关节运动到下一个关节位置点。
-
分析第1次机器人末端到达实际位置点与期望点的坐标位置关系，为了保证期望点处于构建的网格模型区域范围内，且构建网格模型的粒度点之间的间距符合1mm~3mm的机器人平面绝对定位精度指标，取k=16。其补偿策略演示图如图 4所示。
Figure 4. Control strategy of compensation
-
(1) 求最大距离误差的最小值。机器人末端到达P1点后，计算E1, E2, E3, E4与P0的距离误差，并选择最小距离误差的粒度点为下一次移动选择点，公式如下：
$ {\varepsilon _i}\left( {{P_0}} \right) = \min \left\{ {d\left( {{P_0};{P_1}} \right),i \in N} \right\} + {\rm{rad}}\left( {{D_i}} \right) $
(9) $ d\left( {{P_0};{P_i}} \right) = \sqrt {{{\left( {{x_i} - {x_0}} \right)}^2} + {{\left( {{y_i} - {y_0}} \right)}^2}} $
(10) 式中，εi(P0)(1≤i≤20)代表期望点与机器人末端进入到的圆形区域εi之间最大距离误差的最小值; d(P0; Pi)代表P0与设置的粒度点Pi两点之间的距离; rad(Di)代表圆形区域εi的半径Di，通过结果对比得到εi(P0)的最小值。
(2) 确定粒度点的收敛方向。得出最小εi(P0)代表的粒度点的关节空间位置，与机器人实际末端关节位置对比分析，沿着设定的网格模型网格边线的运动矢量驱动机器人运动。若计算的结果表明粒度点P2离期望点的距离最近，机器人末端运动则由P1点移动到P2点, 其运动方向与矢量S1的方向一致。若当期望点P0与构建的网格模型4个粒度点之间的距离依然是机器人末端实际位置点最小，保持机器人末端位置不动，以此时机器人末端的粒度点作为下一步构建网格模型的起始点。
(3) 调整粒度点之间的间距大小。若步骤(1)计算得到粒度点P2离期望点P0的距离误差最小, 选择P2作为网格模型的起始点，调整起始网格模型粒度点间距大小。由于构建网格模型的粒度点间距在关节空间与笛卡尔空间中存在着等比列缩放映射关系，在笛卡尔空间中，水平方向按照矢量S1大小选取‖S1‖/2，在竖直方向按照矢量S2大小选取‖S2‖/2缩小间距，则在关节空间中粒度点的间距按照此前粒度点间距的一半构建模型。
(4) 循环查找最小距离粒度点。重复上述步骤(1)~步骤(3)4次，直到最后一次构建的网格模型相邻粒度点关节空间的间距，在轴1上只相差一个指令单位关节度数Δ1，在轴2上只相差一个指令单位关节度数Δ2。再重复步骤(1)最后一次，计算得到的最小距离误差的粒度点，并驱动机器人到达此点。
(5) 对单一固定期望点多次重复上述步骤(1)~步骤(4), 记录机器末端分别在1轴和2轴累计偏移量，求取其平均值作为补偿量修改其原有控制系统的参量，从而提高系统的平面定位精度。
-
在上述方法中, 可能会出现两种特殊的情况：(1)当期望点P0处于由3个粒度P1, P3, P4组成外接圆的圆心Ω处; (2)当期望点P0处于构建的网格模型类似矩形的平行四边形中心。
这两种情况都不能再按照上述的方法进行构建模型，而是要做适当的调整。当期望点P0处于由3个粒度点P1, P3, P4组成外接圆圆心Ω处，如图 5所示。
$ {\varepsilon _{\min }}\left( {{P_0}} \right) = {\varepsilon _{\min }}\left( {{\mathit{\Omega }_0}} \right) = \mathit{\Omega }{P_i} + {\rm{rad}}\left( {{D_i}} \right) $
(11) 
Figure 5. Structure of desire point located in the center of circumcircle
由于‖P0-P1‖=‖P0-P3‖=‖P0-P4‖, 此时会牵扯出一个最短行程问题：由P2点在P1, P3, P4中确定下一个粒度点时，与P2最短距离的粒度点才是实际被选择点。如图 5可知，P2→P1和P2→P4的距离取决于平行四边形的边长长度，即运动矢量S1，S2模的大小所决定。并且很容易知道P2→P1的距离远比P2→P1→P3的距离小。
期望点P0处于确定的网格模型在笛卡尔空间组成的平行四边形的对角线交点处时，如图 6所示。
Figure 6. Structure of desire point located in the center of grid model
为了保证精度，此时一般情况下的步骤(2)不能采用，要做适当的改进。构建网格模型的粒度点在关节空间中间距大小为此前模型粒度点间距的3/4倍。
-
搭建的实验平台如图 7所示，相机1获取坐标位置，相机2记录末端移动轨迹，部件3是SCARA机器人本体结构。
Figure 7. Experiment system
SCARA机器人的物理参量如下：l1=500mm; l2=500mm; θ1=π/3;θ2=π/6;k=16;Δ1=0.01°=π/1800;Δ2=0.01°=π/1800。
对于给定的起始目标关节位置${P_1}\left( {\frac{{\rm{ \mathsf{ π} }}}{3}, \frac{{\rm{ \mathsf{ π} }}}{6}} \right)$，由视觉传感器得到的3组期望点的坐标分别是：(1)x0=247.8500mm; y0=933.4200mm; (2)x0=248.4800mm; y0=933.0750mm; (3)x0=249.8500mm; y0=933.0300mm。其仿真结果分别如图 8所示。
Figure 8. Simulation results of compensation strategy:relationships between desire point and set point
图 8a~图 8c分别表示SCARA机器人3个不同期望点位置在采用本文中方法的最终补偿策略效果图。由图 8可知，本方法能保证处于起始网格模型区域范围内的期望点最终皆收敛于以一个指令单位步长为间距的网格模型中，且在模型粒度点间距较大时实现了快速收敛，在模型粒度点间距较小时精准定位。
图 9a~图 9c分别表示选择的粒度点在x，y轴上变化曲线。整体上粒度点x，y轴坐标的变化趋势是越来越接近期望点的坐标。当模型粒度点间距较小时, 其重复定位精度对最大距离误差的最小值计算影响较大，多次针对同一个期望点，寻找最后一次构建的网格模型实际被选择的粒度点坐标位置会出现一定的变化。
Figure 9. Change curve of x, y coordinates data
表 1中的3组数据分别表示在不同期望点坐标下步骤(1)确定的粒度点坐标以及最后的最小距离误差。其中a组数据的第(2)步~第(3)步的数据变化表明, 机器末端只在竖直方向发生了变化，水平方向保持不变; 而第(3)步~第(4)步的数据变化表明, 机器末端在水平和竖直方向均发生移动; c组数据前3步的坐标数据一样，表明前3次构建的网格模型，此点位置均是离期望点最近粒度点位置。均符合步骤(2)设定的粒度点收敛方向。
Table 1. Coordinates of the specific steps and the minimum error
test group desire point/mm first step/mm second step/mm third step/mm last step/mm min-error/mm a 247.8500 247.3936 247.9989 247.9989 247.8476 0.0265 933.4200 933.7072 933.3594 933.3594 933.4464 b 248.4800 248.6037 248.6037 248.6037 248.4526 0.0358 933.0750 933.0108 933.0108 933.0108 933.0980 c 249.8500 250.0000 250.0000 250.0000 249.8255 0.0275 933.0300 933.0127 933.0127 933.0127 933.0127 由图 10b和图 10e中的机器末端与图 10a中期望点的距离大小明显可以发现，采用补偿后的机器末端离期望点的距离较未补偿之前的距离近。
Figure 10. Experiments of compensation strategy
通过对表 2中的数据分析可以得知，补偿后机械末端离期望点的距离较补偿前更近，最后的粒度点与期望点的平均绝对定位误差为0.081mm, 较现有的SCARA机器人绝对定位精度有较大提高，再次证明了方法的有效性。
Table 2. Measurement data and error data
group
numbergather
position/
mmbefore
compensation/
mmbehind
compensation/
mmerror/
mmfirst
group243.457 243.055 243.542 0.095 932.466 932.133 932.430 second
group253.335 252.985 253.305 0.089 940.273 940.013 940.194 third
group273.354 273.121 273.403 0.074 963.675 963.213 963.634 fourth
group275.383 274.985 275.343 0.065 967.467 967.153 967.455 -
针对SCARA机器人平面定位精度低的现象，提出了一种SCARA机器人平面定位误差补偿方法。通过在关节空间中构建网格模型并结合最小距离误差逼近，循环查找网格模型中最小距离粒度点，依次驱动机器人末端运动。实验结果表明，此方法只需要知道SCARA机器人平面定位简化模型，弥补了模型不精准的影响，不改变SCARA机器人本体的重复定位精度、但却能提高绝对定位精度, 且在绝对定位误差大的情况下实现快速收敛，在绝对定位误差小的情况下实现精准的定位。但是该方法的缺陷是最后走点的位置只是最接近期望点的位置，而不直接是期望点的位置。在空载情况下，其重复定位精度只对最后一步影响较大，缺少对负载情况下的深入探讨，下一步的工作重心将在研究负载情况下的重复定位精度对模型平面定位精度的影响。
视觉引导的装配机器人平面定位补偿方法
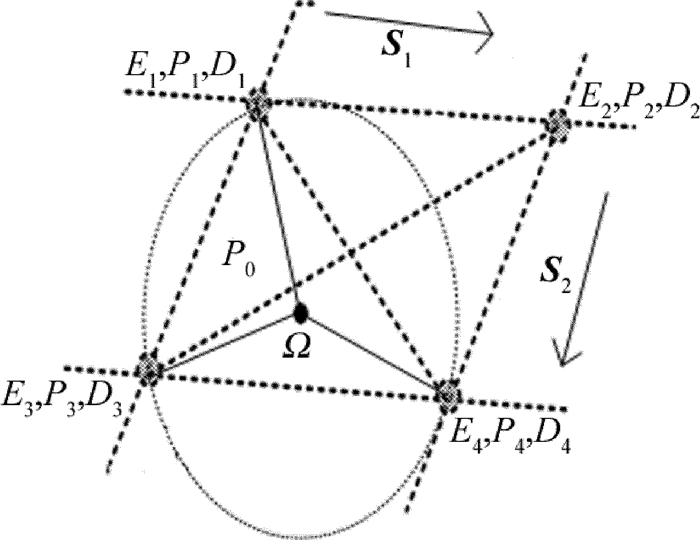
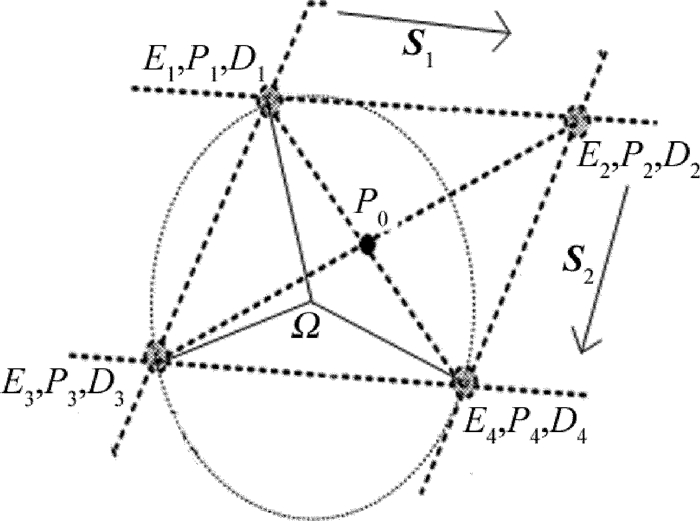
Plane positioning compensation method for assembly robot with visual guiding
-
摘要: 为了提高选择顺应性装配机器手臂（SCARA）机器人平面定位的精度，采用网格模型结合最小距离误差逼近的方法，首先构建SCARA机器人平面定位的简化模型，概述网格模型构建原理，然后通过视觉采集机器人末端第1次到达的实际点与期望点相对位置关系，构建可变参量的起始网格模型，再采用最小距离误差逼近，求解下一步构建可变参量网格模型起始点，最后由期望点在网格模型中位置分布情况决定模型粒度点的收敛更新方向。结果表明，视觉引导的定位补偿策略弥补了因模型不精准而造成的平面定位精度不高的现象；空间插值补偿法定位精度为1mm~3mm，平面定位补偿精度较之有较大提高。该方法调节的参量单一、机器末端移动次数明确、工业应用性强。Abstract: In order to improve the plane positioning accuracy of selective compliance assembly robot arm (SCARA) robot, the method combined compensation strategy based on grid model and the minimum error approximation principle was proposed. Firstly, a simplified model for SCARA robot was established and grid model principle was summarized. Secondly, an initial grid model was constructed by analyzing the location relationship between the first-time reached actual point and the desired point. The starting point of the variable parameter grid model in the next step was constructed by using the minimum distance error approximation method. Finally, the convergence and update direction were determined by the location of the desired point in grid model. The results show that the positioning compensation strategy of visual guidance makes up the phenomenon that the plane positioning accuracy is not high because of the inaccuracy of the model. The accuracy of the positioning compensation strategy is much better than 1mm~3mm of the spatial interpolation compensation method. The proposed method has brief parameter regulation, clearly mobile times and strong industrial application.
-
Figure 8. Simulation results of compensation strategy:relationships between desire point and set point
a—the first group b—the second group c—the third group
Figure 9. Change curve of x, y coordinates data
a—the first group b—the second group c—the third group
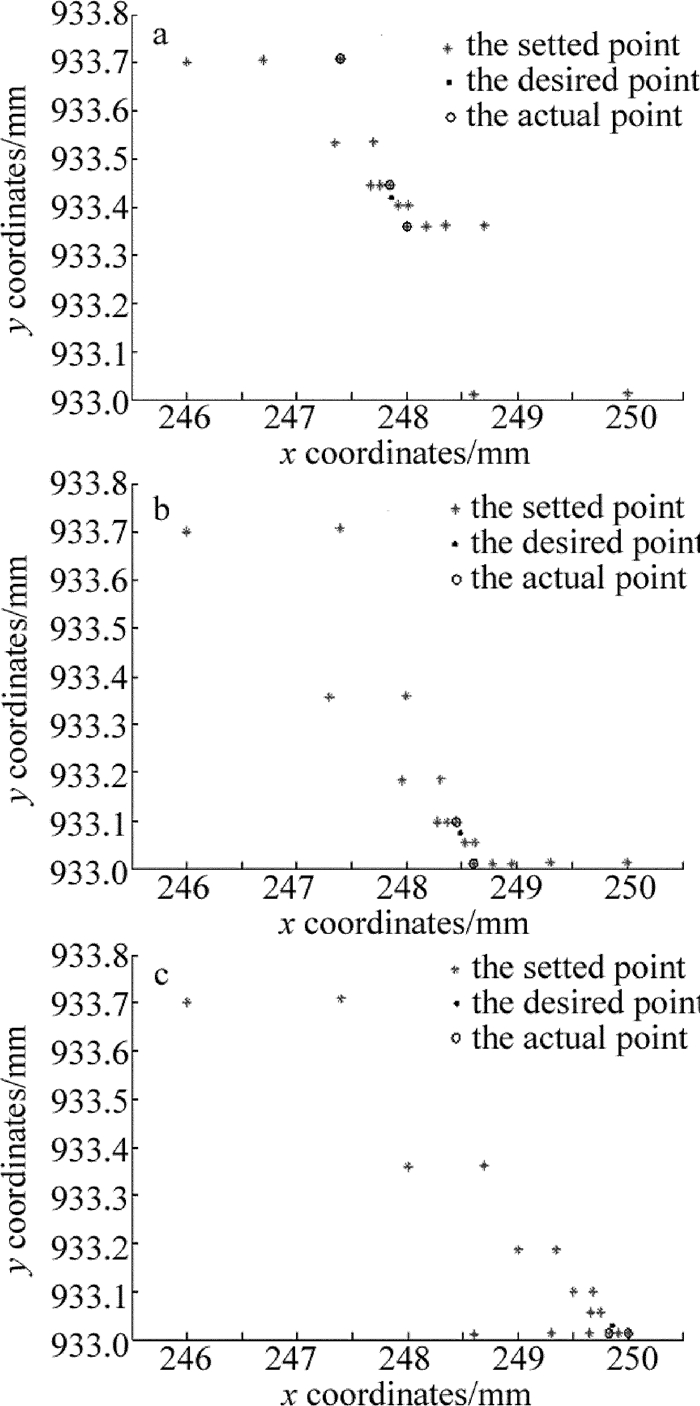
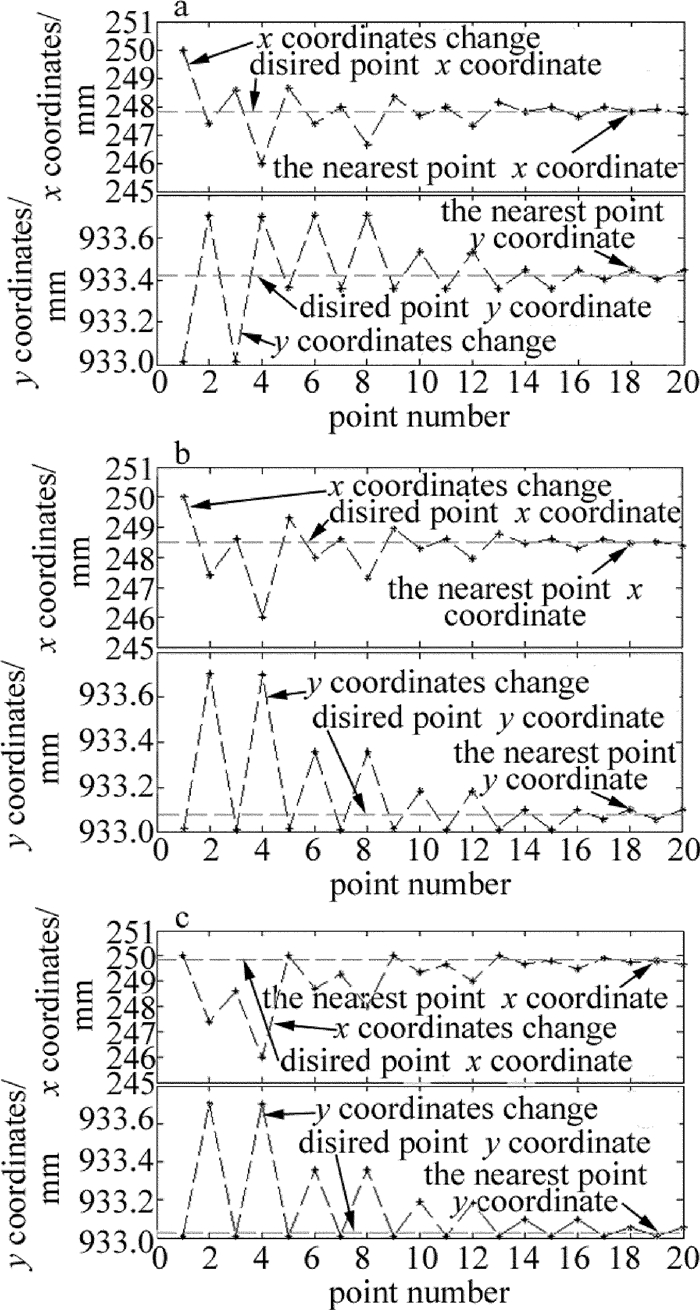
Table 1. Coordinates of the specific steps and the minimum error
test group desire point/mm first step/mm second step/mm third step/mm last step/mm min-error/mm a 247.8500 247.3936 247.9989 247.9989 247.8476 0.0265 933.4200 933.7072 933.3594 933.3594 933.4464 b 248.4800 248.6037 248.6037 248.6037 248.4526 0.0358 933.0750 933.0108 933.0108 933.0108 933.0980 c 249.8500 250.0000 250.0000 250.0000 249.8255 0.0275 933.0300 933.0127 933.0127 933.0127 933.0127 
下载: 导出CSV
Table 2. Measurement data and error data
group
numbergather
position/
mmbefore
compensation/
mmbehind
compensation/
mmerror/
mmfirst
group243.457 243.055 243.542 0.095 932.466 932.133 932.430 second
group253.335 252.985 253.305 0.089 940.273 940.013 940.194 third
group273.354 273.121 273.403 0.074 963.675 963.213 963.634 fourth
group275.383 274.985 275.343 0.065 967.467 967.153 967.455
下载: 导出CSV
-
[1] GINANI L, MOTTA J. Theoretical and practical aspects of robot calibration with experimental verification[J].Brazilian Society of Mechanical Sciences and Engineering, 2011, 8(4):15-21. [2] NUBIOIA A, BONEV I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J].Robotics and Computer-Integrated Manufacturing, 2013, 29(1):236-245. doi: 10.1016/j.rcim.2012.06.004 [3] ZHAO Y M, LIN Y, XI F, et al. Calibration-based iterative learning control for path tracking of industrial robots[J].IEEE Transactions on Industrial Electronics, 2015, 62(5):2921-2929. doi: 10.1109/TIE.2014.2364800 [4] ZHEN H W, HUI X, GUO D C, et al. A distance error based industrial robot kinematic calibration method[J]. Industrial Robot:An International Journal, 2014, 41(5):439-446. doi: 10.1108/IR-04-2014-0319 [5] JOUBAIR A, BONEV I A. Non-kinematic calibration of a six-axis serial robot using planar constraints[J]. Precision Engineering, 2015, 40:325-333. doi: 10.1016/j.precisioneng.2014.12.002 [6] WU B, SU X Y. A precise guiding method for automatic measurement with visual guiding theodolites[J]. Laser Technology, 2015, 39(4):453-457(in Chinese). [7] CHEN M L. Error analysis of thread measurement with machine vision[J]. Laser Technology, 2014, 38(1):109-113(in Chinese). [8] ZHANG H H, LI Y, ZHANG H Y, et al.Calibration of PMP system using virtual planes[J].Laser Technology, 2010, 34(5):600-602(in Chinese). [9] XU A Ch, CHEN J B, ZHANG P M, et al. Ocular aberrations measurement method combined with subjective visual compensation[J]. Laser Technology, 2010, 34(6):774-777(in Chinese). [10] ZHOU W, LIAO W H, TIAN W, et al. Robot accuracy compensation method of spatial grid for aircraft automatic assembly[J]. China Mechanical Engineering, 2012, 23(19):2306-2311(in Chinese). [11] ZHOU W, LIAO W H, TIAN W. Theory and experiment of industrial robot accuracy compensation method based on spatial interpolation[J]. Journal of Mechanical Engineering, 2013, 49(3):42-48(in Chinese). doi: 10.3901/JME.2013.03.042 [12] ZHOU W, LIAO W H, TIAN W, et al. Method of industrial robot accuracy compensation based on particle swarm optimization neural network[J]. China Mechanical Engineering, 2013, 24(2):174-179(in Chinese). [13] YIN X Y, YIN G F, HU X B, et al. Positioning accuracy of robot vision system based on support vector machine regression[J]. Journal of Mechanical Engineering, 2011, 47(1):48-54(in Chinese). doi: 10.3901/JME.2011.01.048 [14] ZHANG T, DAI X L. Kinematic calibration of robot based on distance error[J].Journal of South China University of Technology(Natural Science Edition), 2011, 39(11):98-102(in Chinese). [15] HU X K, SONG A G, ZHANG X R, et al. Design of location system for autonomous robot based on grid line[J]. Measurement Control Technology, 2010, 29(9):40-43(in Chinese). -
点击查看大图
图(10) / 表(2)
计量
- 文章访问数: 5573
- HTML全文浏览量: 3495
- PDF下载量: 264
- 被引次数: 0
