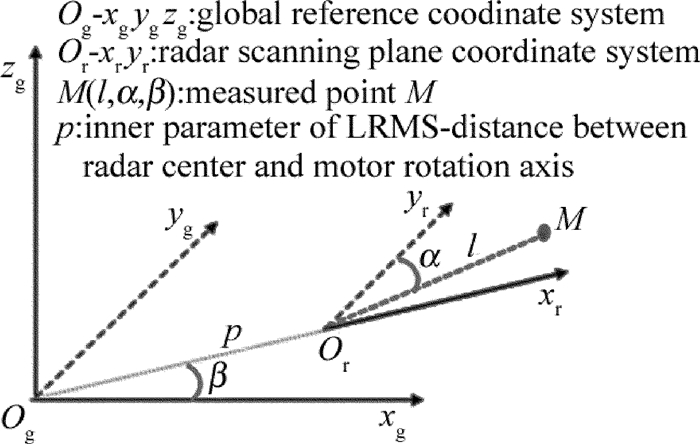
Uncertainty analysis of laser radar measurement system based on error ellipsoid theory
-
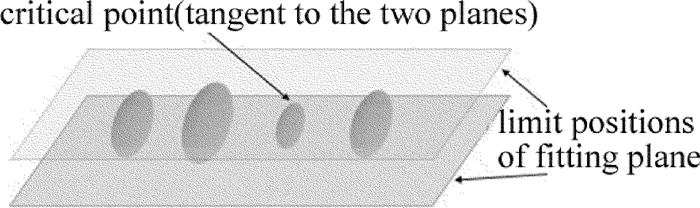
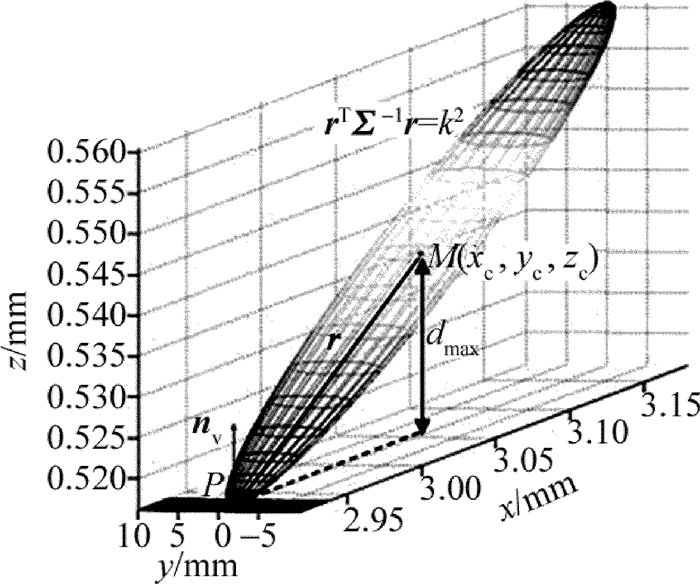
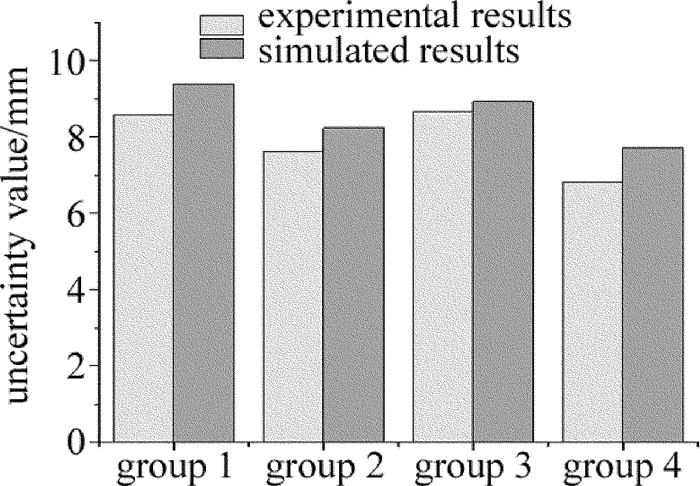
摘要: 为了对3维激光扫描技术的测量精度做出评估，以激光雷达测量系统为研究对象，基于误差椭球理论建立了测量系统的点位误差模型；依据点云平面误差椭球的分布特性，提出了点云拟合平面的不确定度模型，用于评估与拟合平面关联的尺寸测量精度；通过对箱体类物体高度的测量实验，获得了实际测量不确定度，并与模型仿真结果进行了对比。结果表明，该模型可较准确地估算出高度的测量不确定度，从而验证了其有效性及实际意义。Abstract: In order to provide measurement accuracy evaluation for 3-D laser scanning devices, a laser radar measurement system (LRMS) was choosed as the research object and uncertainty model of point cloud fitting plane was proposed. After experimental verification, a single-point error ellipsoid model for the LRMS based on error ellipsoid theory was established. According to the distribution characteristics of plane error ellipsoid of point cloud, uncertainty model of point cloud fitting plane was proposed to evaluate and fit the dimension measurement accuracy associated with plane. Verification experiments were performed by using the LRMS to measure the height of a cubic object, and the measurement accuracy results were evaluated and compared with the simulated results using the proposed uncertainty model. The results show that the model can accurately estimate the uncertainty of height measurement. The research has the validity and practical significance.
-
Keywords:
- measurement and metrology /
- uncertainty /
- error ellipsoid theory /
- laser radar /
- point cloud
-
-
![]()
Figure 2. Mapping relationship between global reference coordinate system and radar scanning plane coordinate system
-
[1] LIANG X L, KANKARE V, YU X W, et al. Automated stem curve measurement using terrestrial laser scanning[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3):1739-1748. DOI: 10.1109/TGRS.2013.2253783
[2] CHEN P. Study on three-dimensional measurement of rotary type workpieces[D].Nanjing: Dongnan University, 2015: 15-20(in Chinese).
[3] ANIL E B, TANG P B, AKINCI B, et al. Deviation analysis method for the assessment of the quality of the as-is building information models generated from point cloud data[J]. Automation in Construction, 2013, 35(1):507-516. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b29aaf179d5780955c87e13fed52372c
[4] JOSÉ-IGNACIO R, SANCHEZ A, GLEZ-DE-RIVERA G, et al. Environment mapping using a 3-D laser scanner for unmanned ground vehicles[J]. Microprocessors and Microsystems, 2015, 39(8):939-949. DOI: 10.1016/j.micpro.2015.10.003
[5] PONZ A, RODRÍGUEZ-GARAVITO C H, GARCÍA F, et al. Laser scanner and camera fusion for automatic obstacle classification in ADAS application[C]//Smart Cities, Green Technologies, and Intelligent Transport Systems: 4th International Conference, SMARTGREENS 2015, and 1st International Conference VEHITS 2015.Basel, Switzerland: Springer International Publishing, 2015: 237-249.
[6] ZHOU S, GUO Y C, GAO Ch, et al. Rapid length measuring system for mobile and large scale cylinder workpieces based on 3-D laser scanning[J]. Optical Precision Engineering, 2014, 22(6):1524-1530(in Chinese). DOI: 10.3788/OPE.
[7] ZHANG Y C, HAN J X, FU X B, et al. Measurement and control technology of the size for large hot forgings[J]. Measurement, 2014, 49(1):52-59. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c577b4fad27a3da507991cefd5658c35
[8] TIAN Zh S, GAO F, JIN Zh L, et al. Dimension measurement of hot large forgings with a novel time-of-flight system[J]. The International Journal of Advanced Manufacturing Technology, 2009, 44(1/2):125-132. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6b7cebd6c8bb5f1bb816ceb7a8b17af8
[9] HE J, GAO F, WU Sh F, et al. Measure dimension of rotating large hot steel shell using pulse laser on PRRR robot[J]. Measurement, 2012, 45(7):1814-1823. DOI: 10.1016/j.measurement.2012.04.001
[10] ZHENG D H, SHEN Y Zh, LIU Ch. 3-D laser scanner and its effect factor analysis of surveying error[J]. Engineering of Surveying and Mapping, 2005, 14(2):32-35(in Chinese). http://en.cnki.com.cn/article_en/cjfdtotal-chgc200502010.htm
[11] CANG Y, JOHANN B. Characterization of a 2-D laser scanner for mobile robot obstacle negotiation[C]//Proceedings of the 2002 IEEE International Conference on Robotics and Automation.New York, USA: IEEE, 2002: 2512-2518.
[12] PARK J H, SHIN Y D, BAE J H, et al. Spatial uncertainty model for visual features using a KinectTM sensor[J]. Sensors, 2012, 12(7):8640-8662. DOI: 10.3390/s120708640
[13] WEI Y F. Surface reconstruction and quality evaluation based on laser radar system[D]. Shanghai: Shanghai Jiaotong University, 2009: 35-60(in Chinese).
[14] SHI W Zh. Models and algorithms for three dimensional spatial information system[M].Beijing:Publishing House of Electronics Industry, 2007:227-230(in Chinese).
[15] DU Zh Ch, WEI Y F, YAO Zh Q. Accuracy analysis of laser radar measurement system based on error ellipsoid model[J]. Journal of Shanghai Jiaotong University, 2009, 43(12):1882-1885(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK200902690637
[16] WANG B, SHI W Zh, MIAO Z L. Confidence analysis of standard deviational ellipse and Its extension into higher dimensional euclidean space[J]. Public Library of Science, 2015, 10(3):1-17. http://pubmedcentralcanada.ca/pmcc/articles/PMC4358977/
[17] FISCHLER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM, 1981, 24(6):381-395. DOI: 10.1145/358669.358692
下载:
计量
- 文章访问数: 5
- HTML全文浏览量: 1
- PDF下载量: 26