Study on numerical simulation of residual stresses induced by laser shock processing
-
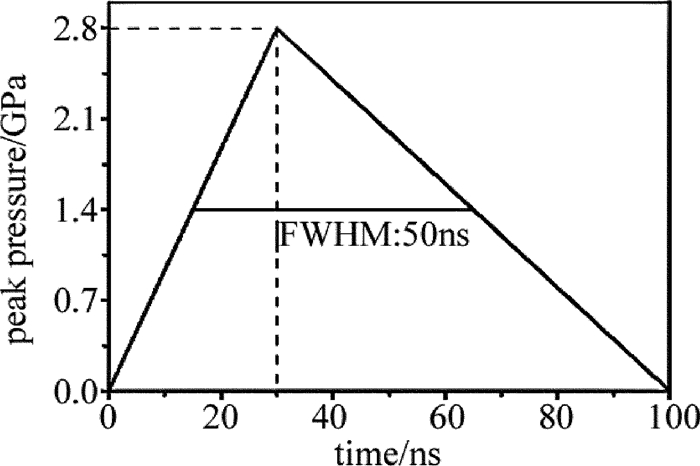
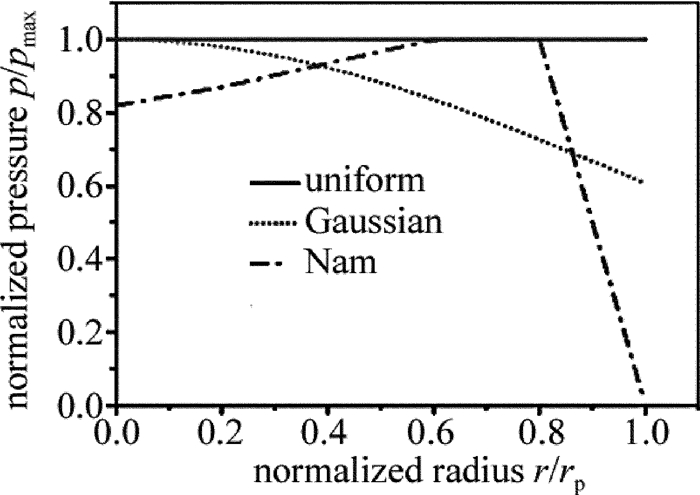
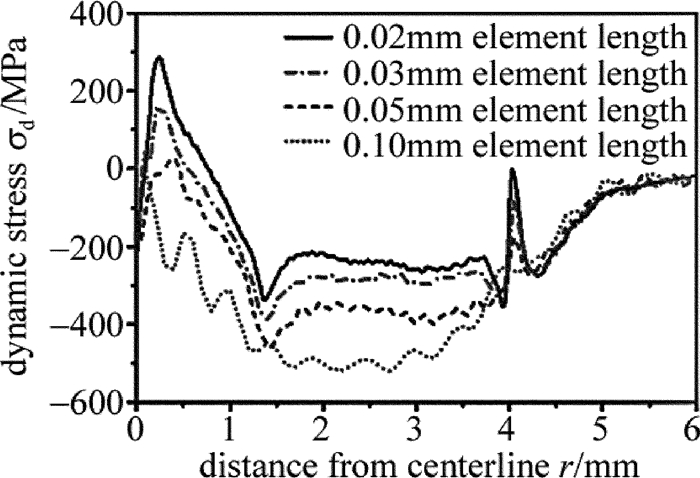
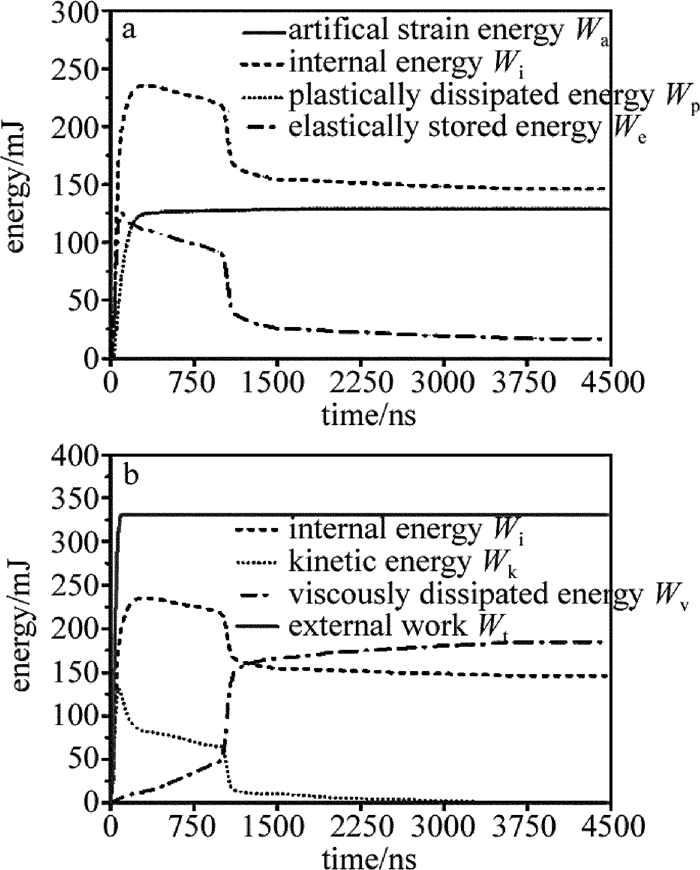
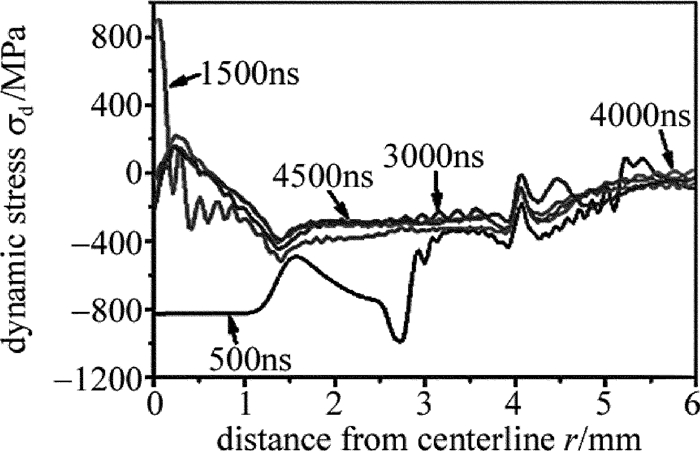
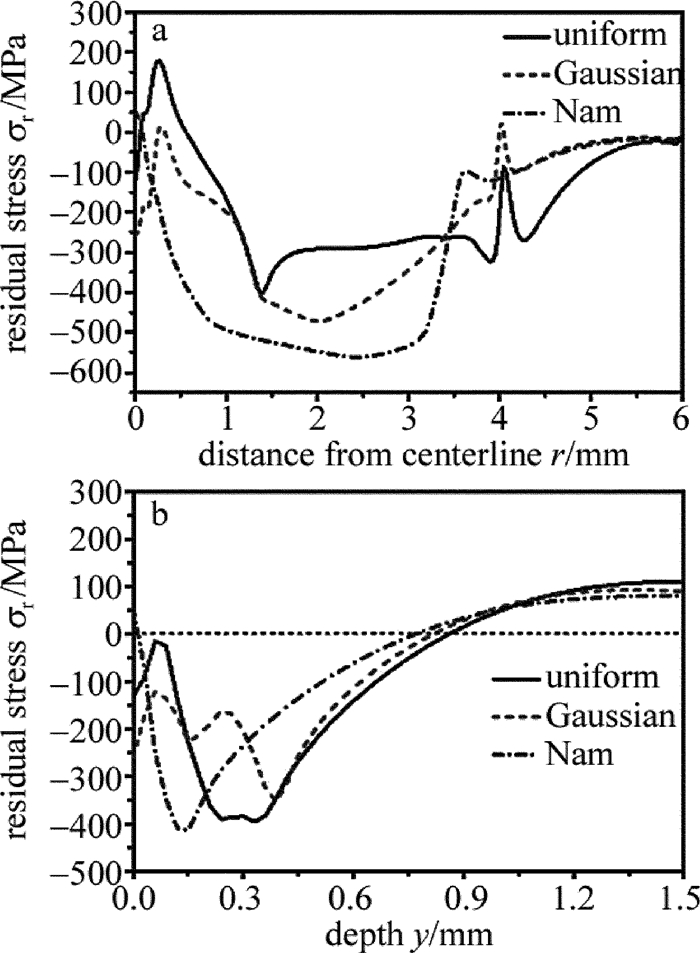
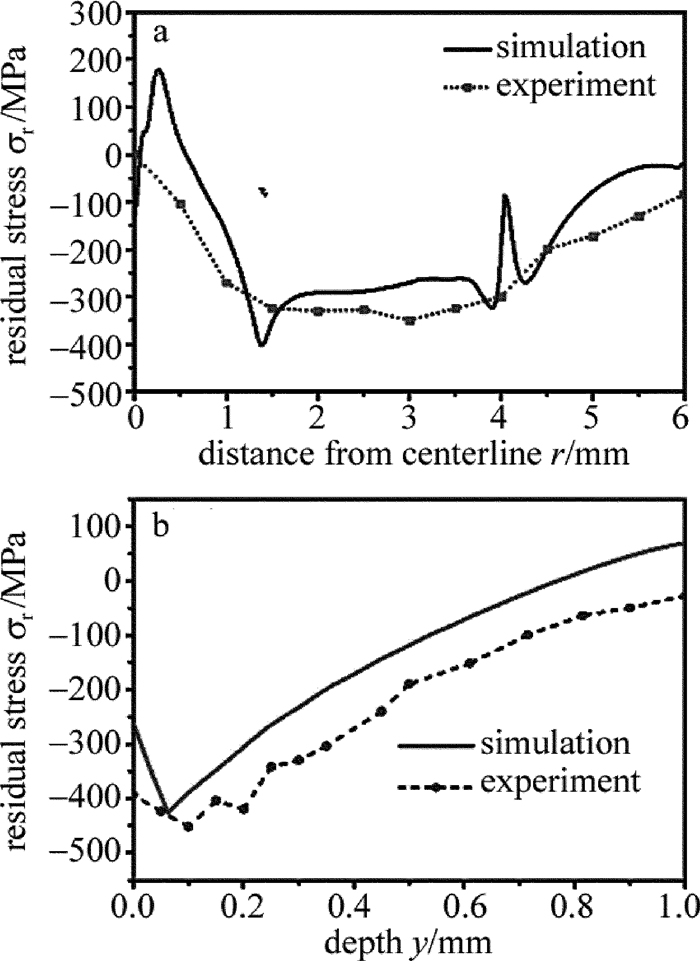
摘要: 为了获得激光冲击强化诱导的残余应力场，采用数值模拟的方法，建立了单次激光冲击强化35CD4合金钢厚板2维轴对称有限元模型，对激光冲击过程中材料内部的能量变化、表面动态应力进行了分析，验证了显式动态求解时间选取的合理性，并讨论了模型网格单元尺寸、冲击压力空间分布模型选取对残余应力模拟结果的影响。结果表明，为了得到收敛的模拟结果，选用的网格单元尺寸应为0.03mm左右。单次圆斑激光冲击的残余应力计算结果与已知的实验测量结果吻合得较好。Abstract: In order to obtain the residual stress field induced by laser shock processing(LSP), the numerical simulation method was used. A 2-D and axisymmetric finite element analysis(FEA)model of single laser shock processing on 35CD4 thick parts was established. History of the energies of material during dynamic analysis and surface dynamic stresses at different times were analyzed to validate the reasonability of the total time of dynamic analysis. The effect of mesh refinement and spatial distribution models of the loading on the simulation results were discussed. The results show that the element length should be around 0.03mm to get convergent results. The predicted results for single LSP with round laser spot are consistent with the available experimental data.
-
Keywords:
- laser technique /
- laser shock processing /
- numerical simulation /
- residual stresses
-
-
![]()
Figure 7. Distribution of residual stresses of different spatial distribution models of the loading
a—on the surface b—along the depth at the center of the laser spot
![]()
Figure 8. Residual stresses comparison between simulation and experiment
a—on the surface b—along the depth at a distance of 3.5mm from centerline
Table 1 Configurations of four meshed finite element models
finite element model finite element infinite element element length Le /mm mesh densityLe/rp A 60×60 2×60 0.10 2.5% B 120×120 2×120 0.05 1.25% C 200×200 2×200 0.03 0.75% D 300×300 2×300 0.02 0.5% 
下载: 导出CSV
-
[1] YANG X H, TANG X D, XUE M Q. Effect of laser shock on residual stress of diesel engine crankshaft chamfer[J]. Laser Technology, 2010, 34(5):596-599(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201005007.htm
[2] LI Y H. Laser shock processing theory and technology[M]. Beijing:Science Press, 2013:11-16(in Chinese).
[3] BRAISTED W, BROCKMAN R. Finite element simulation of laser shock peening[J]. International Journal of Fatigue, 1999, 21(7):719-724. DOI: 10.1016/S0142-1123(99)00035-3
[4] NAM T. Finite analysis of residual stress field induced by laser shock peening[D]. Columbus, USA: The Ohio State University, 2002: 54-76.
[5] HU Y, YAO Z, HU J. 3-D FEM simulation of laser shock processing[J]. Surface and Coatings Technology, 2006, 201(3):1426-1435. http://www.sciencedirect.com/science/article/pii/s0257897206001575
[6] BHAMARE S, RAMAKRISHNAN G, MANNAVA S R, et al. Simulation-based optimization of laser shock peening process for improved bending fatigue life of Ti-6Al-2Sn-4Zr-2Mo alloy[J]. Surface and Coatings Technology, 2013, 232(232):464-474. http://www.sciencedirect.com/science/article/pii/S0257897213004957
[7] ACHINTHA M, NOWELL D. Eigenstrain modelling of residual stresses generated by laser shock peening[J]. Journal of Materials Processing Technology, 2011, 211(6):1091-1101. DOI: 10.1016/j.jmatprotec.2011.01.011
[8] JIANG Y F, DING B, CHENG Zh J, et al. Effect of laser peening area on residual stress field in small-hole specimens[J]. Laser Technology, 2014, 38(2):201-204(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201402012.htm
[9] SHEN L D, CHEN J F, LI X Ch, et al. Finite element analysis on residual stress field for laser shock processing AM50 magnesium alloy[J]. Laser Technology, 2012, 36(1):45-49(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201201014.htm
[10] PEYRE P, FABBRO R, MERRIEN P, et al. Laser shock processing of aluminum alloys. Application to high cycle fatigue behavior[J]. Materials Science and Engineering, 1996, A210(1/2):102-113. http://www.sciencedirect.com/science/article/pii/0921509395100849
[11] WEI X L, LING X. Numerical modeling of residual stress induced by laser shock processing[J]. Applied Surface Science, 2014, 301(20):557-563. http://www.sciencedirect.com/science/article/pii/S0169433214004322
[12] BALLARD P. Residual stresses induced by rapid impact-applications of laser shocking[D]. Palaiseau, France: Ecole Polytechnique, 1991: 20-56.
[13] ZHANG W, YAO Y L, NOYAN I C. Microscale laser shock peening of thin films, part 1:experiment, modeling and simulation[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1):10-17. DOI: 10.1115/1.1645878
[14] KHAN A S, SUH Y S, KAZMI R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12):2233-2248. DOI: 10.1016/j.ijplas.2003.06.005
[15] ZERILLI F J. Dislocation mechanics-based constitutive equations[J]. Metallurgical and Materials Transactions, 2004, A35(9):2547-2555. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ024678004/
[16] JIANG Y F, LAI Y L, ZHANG L, et al. Investigation of residual stress hole on a metal surface by laser shock[J]. Chinese Journal of Lasers, 2010, 37(8):2073-2079(in Chinese). DOI: 10.3788/CJL
-
期刊类型引用(2)
1. 何小波，焦石. 基于相位调制技术的可见光通信系统码间干扰识别研究. 激光杂志. 2021(01): 144-148 . 
百度学术
2. 韩中达，赵黎，王栋，杨博瑞. 兼顾照明的可见光流媒体信息传输装置研究. 激光杂志. 2020(07): 128-132 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 7
- HTML全文浏览量: 2
- PDF下载量: 25
- 被引次数: 2