非相干叠加光束携带<i>C</i>点偶极子的演化特性

陈海涛; 李婷; 高曾辉

doi:10.7510/jgjs.issn.1001-3806.2022.05.019

非相干叠加光束携带C点偶极子的演化特性

1.
成都师范学院物理与工程技术学院, 成都 611130
2.
宜宾学院计算物理四川省高校重点实验室, 宜宾 610064

基金项目:

四川省教育厅自然科学基金资助项目 18ZA0081

国家自然科学基金资助项目 61275203

详细信息

作者简介:
陈海涛(1967-), 男, 博士, 教授, 现主要从事激光传输与控制的研究。E-mail: chqcht@sina.com

中图分类号: TN241
计量
- 文章访问数: 5
- HTML全文浏览量: 1
- PDF下载量: 5
出版历程
- 收稿日期: 2021-06-20
- 修回日期: 2021-08-29
- 发布日期: 2022-09-24

The evolution of C-dipole by incoherent superposition beams

1.
College of Physics and Engineering, Chengdu Normal University, Chengdu 611130, China
2.
Key Laboratory of Computational Physics, Yibin University, Yibin 644000, China

摘要

摘要: 为了探讨非相干叠加光束携带C点偶极子的演化特性, 推导了携带C点偶极子的高斯光束非相干叠加传输表达式, 并进行了数值模拟研究。结果表明, 构成C点偶极子的两个C点的位置和偏振度会随着相关参数的变化而改变; 在旁轴情形下, 没有C点产生和湮灭, 并且这两个C点连线的斜率随着传输距离的增加而单调增加; 在非旁轴情形下, 当光束传输到z= 0.01z_R时, 有多个C点偶极子产生, 在z=10.39z_R时又出现C点偶极子的湮灭; 在瑞利距离z_R处, 光腰半径增加到0.222μm和0.56μm时分别出现C点偶极子的产生和湮灭; 随着离轴距离和光束波长的变化, 也出现C点的产生和湮灭。研究结果对深入理解偏振奇点矢量光束和寻找奇点光学潜在应用具有一定参考价值。
- 激光光学 /
- 奇点光学 /
- 偏振奇点 /
- C点偶极子 /
- 传输
Abstract: The evolution of the incoherent superposition of two nonparaxial Gaussian beams carried a C-dipole was theoretically and numerically studied. The results show that the position and degree of polarization of two C-points may change with variation of the relevant parameters. The slope of the axis of the C-dipole increases monotonically with propagation. For the case of non-paraxial beams, creation and annihilation of C-dipoles occur as the beams propagate to 0.01z_R and 10.39z_R, respectively. At the plane z=z_R, the creation and annihilation of C-points respectively occurs when the waist width increases to 0.222μm and 0.56μm. Besides, the creation and annihilation of C-points may take place with variation of the off-axis parameter and the wavelength of the host nonparaxial beams. The results would be useful for deeply understanding singular optics and seeking for their potential applications.
- laser physics /
- singular optics /
- polarization singularities /
- C-dipole /
- propagation

HTML全文

引言

奇点光学主要对光场中出现的位相奇点或者偏振奇点进行研究，由于其在光操纵、原子捕获光干涉度量和显微检测等方面日益重要的应用而成为现代光学的一个重要分支。典型的位相奇点包括螺旋型位错(光涡旋)和刃型位错两种，而光涡旋偶极子被定义为带有相反拓扑电荷的一对光涡旋^[1]。INDEBETOUW研究发现, 构成光涡旋偶极子的两个光涡旋，因带有相反拓扑电荷而在空间传输中相互吸引并湮灭^[1]。FREUND的研究表明：传输过程中湮灭的光涡旋偶极子会在光传输过程中在远场重现^[2]。ROUX采用旁轴近似理论，分别讨论了光涡旋偶极子在自由空间和梯度折射率介质的传输轨迹^[3-4]。LV等人研究了光涡旋偶极子通过像散透镜和半屏衍射的演化特性^[5-6]。

矢量光束中存在的典型偏振奇点有两种: 一是光场中孤立的圆偏振点，定义为C点，从C点起偏振椭圆退化为圆；二是L线，线上点的偏振椭圆退化为线^[7]。实验上可以采用干涉或者衍射的方法，两束非均匀光束进行叠加来产生C点^[8-10]。此外, 偏振奇点也可以由两束单色光束非相干叠加产生^[11-12]。类似于光涡旋偶极子的定义。FREUND将C点偶极子定义为具有对称性并带相反指数I_C为+1/2和-1/2的一对C点，通过相干叠加的方法在光束束腰处嵌入预期的奇点结构，来浮现C点偶极子^[10]。跟光束相干的相干叠加相比，激光束非相干叠加对其相位和偏振没有严格要求，不需要控制光束的相位，结构简单而易于实现^[13]。

稳定激光腔输出的光束属于各类高斯光束，而非稳腔输出的基模光束准直后的远场光强度分布接近高斯分布，因此，高斯光束传输的研究在理论和在工程实践中都有重要意义^[14]。多数奇点光学的研究基于光束传输的旁轴近似理论对奇点的空间演化特性进行讨论。但是，对于拥有大发散角或者跟波长相比拟的小光斑尺寸的光束传输，采用旁轴理论得到结果并不准确，光束传输的非旁轴效应应该予以考虑^[15-18]。因此，作者拟对高斯光束进行非相干叠加得到C点偶极子，对旁轴和非旁轴两种情形下C点偶极子的演化进行理论分析和数值模拟研究，并将两种情形的演化特性进行对比。

1. 理论计算

1.1 旁轴情形

设初始单色矢量电场E由具有相同角频率ω的两束矢量光束E_{0, A}和E_{0, B}非相干叠加构成，它们可以表示为:

$\left\{\begin{array}{l} \boldsymbol{E}_{0, A}=\left(E_{0, A_x} \boldsymbol{i}+E_{0, A_y} \boldsymbol{j}\right) \exp (\mathrm{i} \omega t) \\ \boldsymbol{E}_{0, B}=\left(E_{0, B_x} \boldsymbol{i}+E_{0, B_y} \boldsymbol{j}\right) \exp (\mathrm{i} \omega t) \end{array}\right.$

(1)

式中, i和j分别表示x方向和y方向的单位矢量，t表示时间变量。

在非相干条件下，总电场的斯托克斯参数为各个非相干成分的斯托克斯参数之和^[12]:

$S_l=S_{l, A}+S_{l, B}, (l=0, 1, 2, 3)$

(2)

其中,

$\left\{\begin{array}{l} S_{0, g}=\left|E_{g_x}\right|^2+\left|E_{g_y}\right|^2 \\ S_{1, g}=\left|E_{g_x}\right|^2-\left|E_{g_y}\right|^2 \\ S_{2, g}=2 \operatorname{Re}\left(E_{g_x}^* E_{g_y}\right) \\ S_{3, g}=2 \operatorname{Im}\left(E_{g_x}^* E_{g_y}\right) \end{array}, (g=A, B)\right.$

(3)

式中，Re和Im表示相应函数的实数和虚数部分，*表示对相应函数取复共轭。

光场中的C点位置可以通过对应的斯托克斯标量场来描述^[19]：

$S_{1, 2}=S_1+\mathrm{i} S_2$

(4)

要采用非相干叠加光束在光场中得到C点偶极子，假定初始场成分E_{0, A}和E_{0, B}为：

$\left\{ \begin{array}{l} E_{0, A_x} &=\left(x_0+\mathrm{i} y_0\right) \exp \left[-\left(x_0^2+y_0^2\right) / w_0^2\right] \\ E_{0, A_y} &=\mathrm{i} \exp \left[-\left(x_0^2+y_0^2\right) / w_0^2\right] \\ &E_{0, B_x}=\left(i y_0-s\right) \exp \left[-\left(x_0^2+y_0^2\right) / w_0^2\right]\\ &E_{0, B_y}=\left(y_0-\mathrm{i} s\right) \exp \left[-\left(x_0^2+y_0^2\right) / w_0^2\right] \end{array} \right.$

(5)

式中, w₀为光腰半径, s为离轴距离。将(5)式代入(2)式~(4)式得：

$\begin{aligned} S_{1, 2}=&\left(x_0+s+\mathrm{i} y_0\right)\left(x_0-s-\mathrm{i} y_0\right) \times \\ & \exp \left[-\left(x_0^2+y_0^2\right) / w_0^2\right] \end{aligned}$

(6)

(6) 式表明, 初始平面光场含有奇点指数为±1/2的一对C点偶极子，这两个C点对称位于(-s, 0)和(s, 0)。

在旁轴近似下，采用菲涅耳衍射积分公式，得到平面传输距离z>0处的E_{A_x}, E_{A_y}, E_{B_x}和E_{B_y}为：

$\left\{\begin{array}{l} E_{A_x}=M\left(\frac{v_x+\mathrm{i} v_y}{u}\right) \\ E_{A_y}=\mathrm{i} M s \\ E_{B_x}=M\left(\frac{\mathrm{i} v_y}{u}-s\right) \\ E_{B_y}=M\left(\frac{v_y}{u}-\mathrm{i} s\right) \end{array}\right.$

(7)

其中,

$\left\{\begin{array}{l} M=\frac{-\mathrm{i} \pi}{u \lambda z} \exp \left[\frac{v_x^2+v_y^2}{u}-\frac{\mathrm{i} k}{2 z}\left(x^2+y^2\right)+\mathrm{i} k z\right] \\ u=\frac{1}{w_0{ }^2}+\frac{\mathrm{i} k}{2 z} \\ v_x=\frac{\mathrm{i} k x}{2 z} \\ v_y=\frac{\mathrm{i} k y}{2 z} \end{array}\right.$

(8)

式中，k为与背景光束波长λ有关的波数，k=2π/λ。

将(7)式和(8)式代入(2)式~(4)式, 得到z平面处C点的坐标：

$\left\{\begin{array}{l} x=\frac{-k w_0^2 y}{2 z} \\ y=\frac{-4 s z}{k w_0{ }^6\left(\frac{k^2}{4 z^2}+\frac{1}{w_0^4}\right)} \pm \frac{2 s z}{\sqrt{\frac{4}{w_0^4}+w_0^4}\left(\frac{k^2}{4 z^2}+\frac{1}{w_0^4}\right)} \times \\ \left\{\frac{k^2}{4 z^2}+\frac{1}{w_0^4}\right)^2 \end{array}\right.$

(9)

由(9)式可以看出：在旁轴近似下，虽然携带C点偶极子的两束非相干叠加光束中C点的位置跟传输距离z、光束波长λ、光腰半径w₀以及离轴距离s有关，但并没有出现C点产生和湮灭。这与携带C点偶极子的单一高斯光束的传输特性不同，后者在传输过程中，有新的C点产生和湮灭现象发生^[10]。

由(9)式可知，连接这两个C点的直线斜率可以表示为:

$m=2 z /\left(k w_0^2\right)$

(10)

(10) 式表明, 随着传输距离的增加，连接这两个C点直线的斜率是单调增加的。

1.2 非旁轴情形

在非旁轴情形下，将(5)式代入瑞利-索末菲衍射积分，得z>0平面处的光场为：

$\left\{\begin{array}{l} E_{A_x}= N\left[\frac{-\mathrm{i} k\left(v_x{ }^3+v_y{ }^3\right)}{2 u^3 r}+\frac{k v_x v_y\left(v_x-\mathrm{i} v_y\right)}{2 u^3 r}+\frac{\mathrm{i} k\left(v_x^2 x-\mathrm{i} v_y^2 y\right)}{u^2 r}-\frac{\mathrm{i} k\left(v_x+\mathrm{i} v_y\right)}{u^2 r}-\right.\\ \left.\frac{k v_x v_y(x-\mathrm{i} y)}{u^2 r}+\frac{\mathrm{i} k(x+\mathrm{i} y)}{2 u r}+\frac{v_x+\mathrm{i} v_y(\mathrm{i} k r-1)}{u}\right] \\ E_{A_y}=\mathrm{i} s N\left[\frac{-\mathrm{i} k\left(v_x^2+v_y^2\right)}{2 u^2 r}+\frac{\mathrm{i} k\left(v_x x+v_y y\right)}{u r}-\frac{\mathrm{i} k}{2 u r}+(\mathrm{i} k r-1)\right] \\ E_{B_x}= N\left[\frac{k v_y\left(v_x^2+v_y^2\right)}{2 u^3 r}+\frac{\mathrm{i} k s\left(v_x^2+v_y^2\right)}{2 u^2 r}-\frac{k v_y\left(v_x x+v_y y-1\right)}{u^2 r}-\right.\\ \left.\frac{\mathrm{i} k s\left(v_x x+v_y y\right)}{u r}+\frac{\mathrm{i} k(s+\mathrm{i} y)}{2 u r}+(r k+\mathrm{i})\left(\frac{v_y}{u}+\mathrm{i} s\right)\right] \\ E_{B_y}= N\left[\frac{-\mathrm{i} k v_y\left(v_x^2+v_y^2\right)}{2 u^3 r}-\frac{k s\left(v_x^2+v_y^2\right)}{2 u^2 r}+\frac{\mathrm{i} k v_y\left(v_x x+v_y y-1\right)}{u^2 r}+\right.\\ \left.\frac{k s\left(v_x x+v_y y\right)}{u r}+\frac{\mathrm{i} k(y+\mathrm{i} s)}{2 u r}+(r k+\mathrm{i})\left(\frac{\mathrm{i} v_y}{u}+s\right)\right] \end{array}\right.$

(11)

式中,

$\left\{\begin{array}{l} N=\frac{-z}{2 u r^3} \exp \left[\frac{v_x^2+v_y^2}{u}+\mathrm{i} k r\right] \\ u=\frac{1}{w_0^2}-\frac{\mathrm{i} k}{2 r} \\ v_x=-\frac{\mathrm{i} k x}{2 r} \\ v_y=-\frac{\mathrm{i} k y}{2 r} \\ r=\sqrt{x^2+y^2+z^2} \end{array}\right.$

(12)

比较(7)式和(11)式可以看出，携带C点偶极子的光束非旁轴情形下的传输表达式比旁轴情形复杂得多，并且也不容易得到光束传输过程中的C点位置坐标公式。

2. 数值模拟

2.1 旁轴情形

在数值计算时，C点的奇点指数可以根据符号法则来确定^[20]，其旋向性由斯托克斯参数S₃的正负来判定^[21]，偏振度由下式决定^[22] :

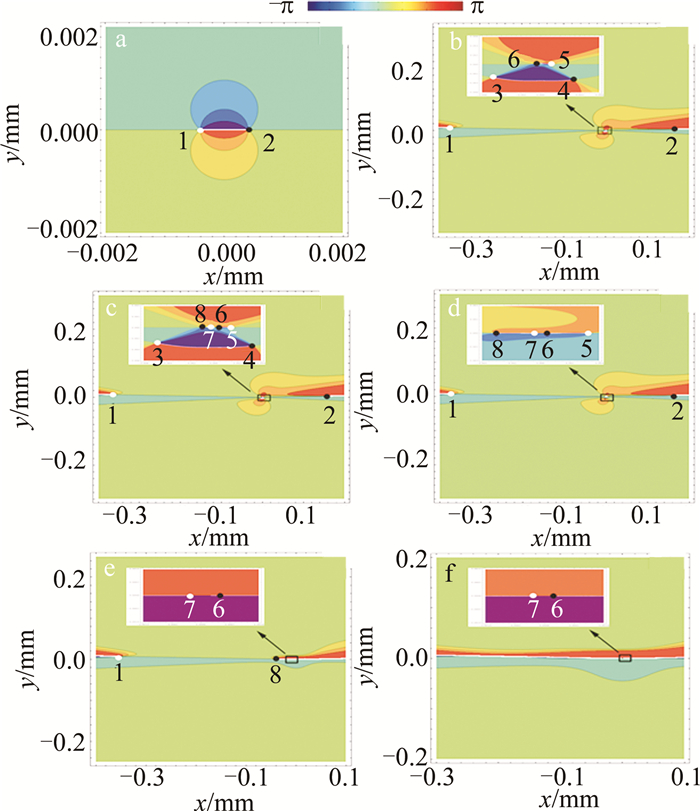
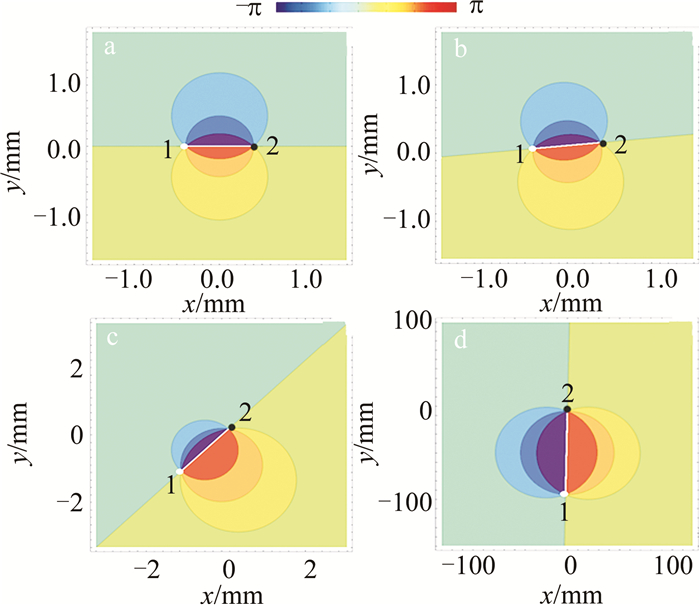
$P=\sqrt{S_1^2+S_2{ }^2+S_3{ }^2} / S_0$

(13)

图 1为旁轴情形下自由空间传输的C点偶极子光束的S_{1, 2}的等位相线图。其中计算参数λ=1050nm, w₀=2mm, s=0.2w₀, 图中用白色小圆点(黑色小圆点)表示奇点指数为+1/2或-1/2的C点。由图 1a可见，与(6)式一致，初始平面z=0出现了有由奇点指数为±1/2的C点1和2构成的C点偶极子，这两个C点对称的位于(-0.4mm, 0mm)和(0.4mm, 0mm), 其旋向性均为+1，偏振度都是1。由传输距离增加到z=0.001z_R(其中z_R=πw₀²/λ²)的图 1b可见，C点1和2移动到分别到位置(-0.41mm, 0.04mm)和(0.41mm, 0.04mm)处。虽然，这两个奇点的旋向性不变，但是它们的偏振度分别变为P=0.008和P=0.97。由图 1a~图 1d可以看出，随着传输距离的增加，连接两个C点的直线斜率不断增加，这与(9)式相一致。因此，随着传输距离的增加，由高斯光束非相干叠加形成的C点偶极子的位置和偏振度可能改变，但并没有新的C点产生。该结论与通过相干高斯光束产生的C点偶极子演化特性不同，后者随着传输距离的增加，会出现C点的产生和湮灭现象^[10]。

Figure 1. Contour lines of phase of S_{1, 2} of the paraxial beams carrying a C-dipole

a—z=0 b—z=0.1z_R c—z=z_R d—z=50z_R

下载: 全尺寸图片幻灯片

2.2 非旁轴情形

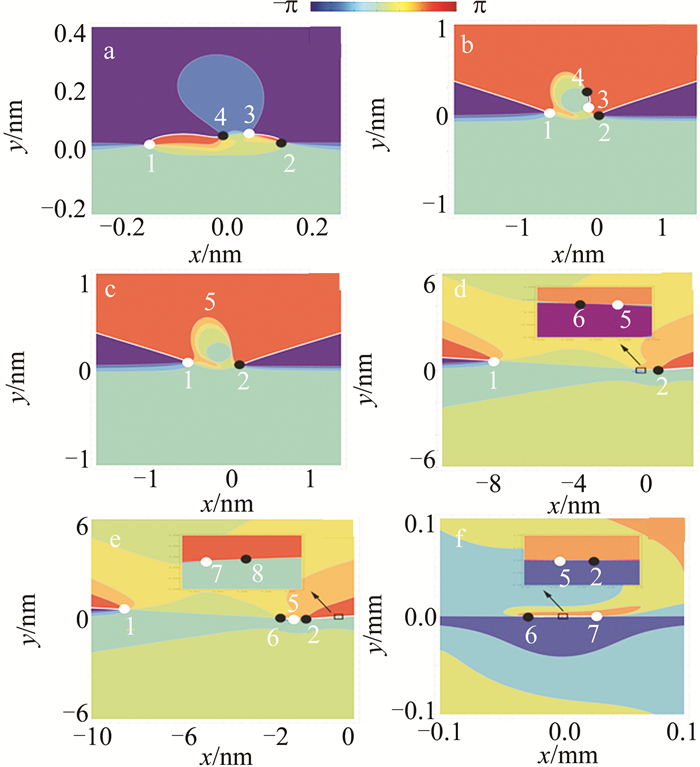
图 2为非旁轴旁轴情形下自由空间传输的C点偶极子光束的S_{1, 2}的等位相线图。为了满足瑞利衍射积分条件，背景高斯光束成分的光腰半径取作w₀=2μm，其它计算参数与图 1相同。当传输距离增加到z=0.01z_R(见图 2b)时，C点1和2分别移动到位置(-0.374mm, 0.008mm)和(0.161mm, 0.003mm)处, 它们的偏振度则由P均为1分别变为0.22和0.27。除了C点1和2之外，光场还出现了C点3, 4, 5和6，它们的奇点指数分别为+1/2, -1/2, +1/2, -1/2，偏振度分别为0.36, 0.35, 0.36, 0.67。当传输距离增加到z=0.042z_R(见图 2c)，光场中除了C点1~6之外，出现了新的C点7和8，这两个奇点的奇点指数分别为+1/2和-1/2，偏振度分别为0.65, 0.57。在此之后，C点3和4因其奇点指数相反和旋向性相同，随着传输距离的增加而相互靠近，直到z=0.5z_R时(见图 2d)最终结合而湮灭。同理，C点2和5在距离传输到z=4.9z_R时(见图 2e)湮灭，C点2和5在距离传输到z=10.39z_R时(见图 2f)湮灭。因此，随着传输距离的增加，非旁轴旁轴情形下C点偶极子光束在传输过程中出现了多对C点的产生和湮灭。这与旁轴情形C点偶极子光束传输特性不同，随着传输距离的增加，旁轴C点偶极子光束中没出现C点产生的产生和湮灭现象。

Figure 2. Contour lines of phase of S_{1, 2} of the nonparaxial beams carrying a C-dipole

a—z=0 b—z=0.01z_R c—z=0.042z_R d—z=0.5z_R e—z=4.9z_R f—z=10.39z_R

下载: 全尺寸图片幻灯片

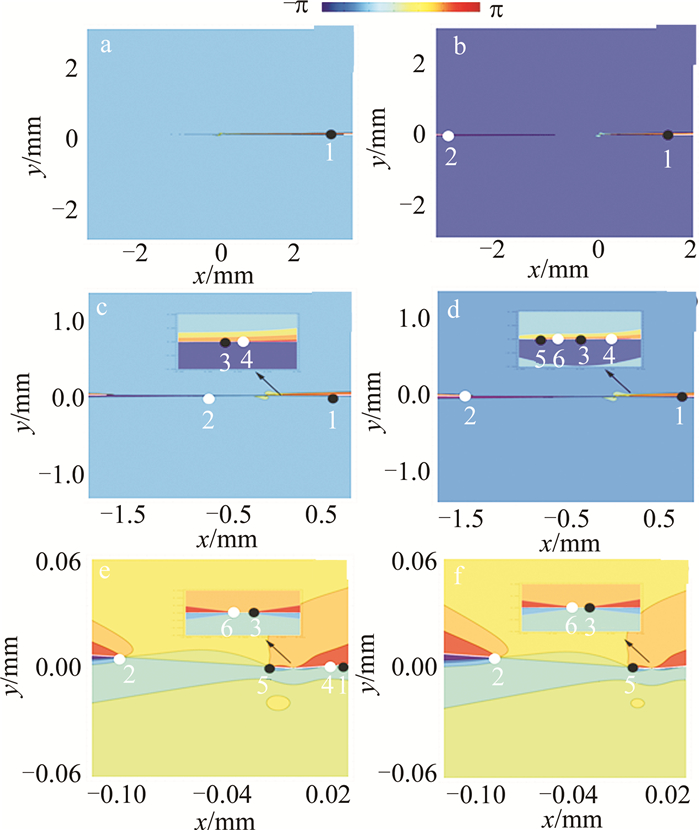
图 3是位置z=z_R处C点偶极子非旁轴光束的S_{1, 2}随其光腰半径w₀变化的等位相线图。其它的计算参数跟图 2相同。由w₀=0.1μm(见图 3a)可以看出，C点1, 2, 3和4出现在光场中，它们的奇点指数分别为+1/2, -1/2, +1/2, -1/2，偏振度分别为0.968, 0.968, 0.342, 0.168。随着w₀增加，C点3和4因带相反的奇点指数相互吸引而靠近(见图 3b)。在w₀增加到0.222μm(见图 3c)时，C点3和4湮灭。但当w₀增加到0.56μm(见图 3d)时，光场出现了一对新的C点5和6，它们带有相反奇点指数+1/2和-1/2，相同偏振度0.75。当w₀增加到0.597μm(见图 3e)时，光场又出现了带有相反奇点指数+1/2和-1/2，相同偏振度0.27的一对C点7和8。此后，随着w₀增加，C点1和8因带有相反拓扑电荷和相同偏振度而彼此靠近而湮灭(见图 3f)。因此，随着光腰半径的变化，有带有相反拓扑电荷和相同偏振度的成对C点产生和湮灭现象发生。这与旁轴情形C点偶极子演化特性不同，由旁轴情形z平面处光场C点坐标(9)式可以看出，旁轴C点偶极子光束中C点的个数不随光腰半径的改变而改变。

Figure 3. Contour lines of phase of S_{1, 2} for different waist widths of the host beams

a—w₀=0.1μm b—w₀=0.221μm c—w₀=0.222μm d—w₀=0.56μm e—w₀=0.597μm f—w₀=6.2μm

下载: 全尺寸图片幻灯片

图 4为非旁轴光束的S_{1, 2}随离轴距离s变化的等位相线图。其它计算参数跟图 2相同。由s=0w₀(见图 4a)可以看出，只有奇点指数为-1/2和偏振度为1的C点1出现在光场中。但是，当离轴距离s增加到0.023w₀(见图 4b)时, 除了C点1之外，奇点指数为+1/2和偏振度为1的C点2也出现在光场中。当离轴距离s增加到0.044w₀(见图 4c)时, 光场中产生一对新的C点偶极子3和4，它们的奇点指数为-1/2和+1/2，偏振度均为1。当离轴距离s增加到0.05w₀(见图 4d)时, 光场中又出现一对C点偶极子5和6，它们的奇点指数为-1/2和+1/2，偏振度均为1。随着离轴距离s增加，C点1和4因带有相反拓扑电荷和相同偏振度而彼此靠近而湮灭。这说明：随着离轴距离的变化，非旁轴光束中不仅出现成对C点的产生和湮灭，也有单个C点的产生。该结论与通过相干高斯光束产生的C点偶极子演化特性不同，后者没有单个C点的产生或湮灭^[10]。这与旁轴情形C点偶极子演化特性不同，由旁轴情形z平面处光场C点坐标(9)式可以看出，旁轴C点偶极子光束中C点的个数不随参数离轴距离的改变而改变。

Figure 4. Contour lines of phase of S_{1, 2} for different off-axis parameter

a—s=0.01w₀ b—s=0.023w₀ c—s=0.044w₀ d—s=0.05w₀ e—s=0.72w₀ f—s=0.73w₀

下载: 全尺寸图片幻灯片

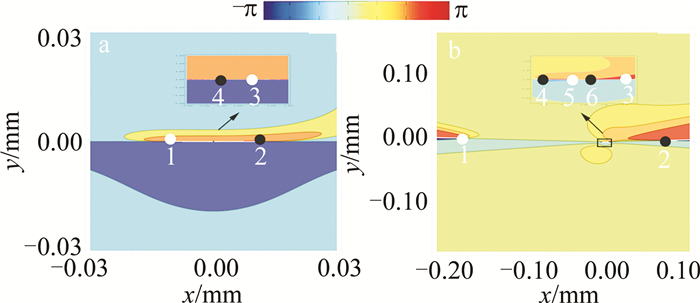
图 5为非旁轴光束的S_1，2随波长λ变化的等位相线图。其它的计算参数跟图 2相同。在波长λ=0.193μm(见图 5a)时，C点1, 2, 3和4出现在光场中，它们的奇点指数分别为+1/2, -1/2, +1/2和-1/2，偏振度分别为0.96, 0.68, 1和1。当波长λ增加到1.55μm(见图 5b)时，在C点3和4之间出现了一对新的C点，它们的奇点指数分别为+1/2和-1/2，偏振度均为1。因此，随着背景光束波长λ的变化，除了C点的位置和偏振度改变外，还有成对的C点产生。这与旁轴情形C点偶极子演化特性不同，由旁轴情形z平面处光场C点坐标(9)式可以看出，旁轴C点偶极子光束中C点的个数不随背景光束波长的改变而改变。

Figure 5. Contour lines of phase of S_{1, 2} for different wavelengths of the host beams

a—λ=0.193μm b—λ=1.55μm

下载: 全尺寸图片幻灯片

3. 结论

通过两束矢量高斯光束的非相干叠加得到了C点偶极子，然后从理论上和数值模拟讨论了旁轴和非旁轴情形下C点偶极子光束的演化特性。研究表明：在旁轴情形下，构成该C点偶极子的C点的位置和偏振度跟光束传输距离、离轴距离和背景光波长有关，连接C点偶极子的轴线斜率随传输距离的增加而单调增加。在非旁轴情形下，当传输距离、离轴距离和背景光束波长变化时，除了C点位置和偏振度可能变化外，还有成对的C点因带有相反奇点指数而接近和湮灭.这些结果与旁轴矢量光束情形类似。但是对于非旁轴情形，光束在传输过程中，光场中出现更多C点，有新的单个C点或者C点偶极子产生。这与旁轴情形C点偶极子演化特性不同，当传输距离、光束波长、光腰半径和离轴距离等参数改变时，旁轴C点偶极子光束中并没出现C点产生的产生和湮灭现象。

非旁轴情形下C点偶极子光束演化特性比旁轴情形丰富和复杂的原因在于, 旁轴情形和非旁轴情形C点偶极子光束的传输遵从不同的传输规律：旁轴光束传输遵从菲涅耳衍射积分公式, 而非旁轴光束传输遵从瑞利-索末菲衍射积分。尽管两种情形的入射C点偶极子光束完全相同，但是两种情形的z>0平面的光场表达式完全不同，非旁轴情形的表达式要复杂得多。这说明非旁轴情形下C点偶极子光束的演化特性比旁轴情形显得更丰富和复杂。研究结果对于深入理解非旁轴矢量光束奇点光学和寻找奇点光学的潜在的应用具有参考价值。

Figure 1. Contour lines of phase of S_{1, 2} of the paraxial beams carrying a C-dipole

a—z=0 b—z=0.1z_R c—z=z_R d—z=50z_R

下载: 全尺寸图片幻灯片

Figure 2. Contour lines of phase of S_{1, 2} of the nonparaxial beams carrying a C-dipole

a—z=0 b—z=0.01z_R c—z=0.042z_R d—z=0.5z_R e—z=4.9z_R f—z=10.39z_R

下载: 全尺寸图片幻灯片

Figure 3. Contour lines of phase of S_{1, 2} for different waist widths of the host beams

a—w₀=0.1μm b—w₀=0.221μm c—w₀=0.222μm d—w₀=0.56μm e—w₀=0.597μm f—w₀=6.2μm

下载: 全尺寸图片幻灯片

Figure 4. Contour lines of phase of S_{1, 2} for different off-axis parameter

a—s=0.01w₀ b—s=0.023w₀ c—s=0.044w₀ d—s=0.05w₀ e—s=0.72w₀ f—s=0.73w₀

下载: 全尺寸图片幻灯片

Figure 5. Contour lines of phase of S_{1, 2} for different wavelengths of the host beams

a—λ=0.193μm b—λ=1.55μm

下载: 全尺寸图片幻灯片

参考文献(22)

[1]	INDEBETOUW G. Optical vortices and their propagation[J]. Journal of Modern Optics, 1993, 40(1): 73-87. DOI: 10.1080/09500349314550101
[2]	FREUND I. Saddle point wave fields[J]. Optics Communications, 1999, 163(4/6): 230-242.
[3]	ROUX F. Paraxial modal analysis technique for optical vortex trajectories[J]. Journal of the Optical Society of America, 2003, B20(6): 1575-1580.
[4]	ROUX F. Spatial evolution of the morphology of an optical vortex dipole[J]. Optics Communications, 2004, 236(4/6): 433-440.
[5]	YAN H W, LV B D. Transformation of the optical vortex dipole by an astigmatic lens[J]. Journal of Optics, 2009, A11(6): 065706.
[6]	GAO Z H, HE D, LV B D. Evolution of an optical vortex dipole diffracted by a half screen[J]. Acta Physica Sinica, 2011, 60(7): 074209 (in Chinese). DOI: 10.7498/aps.60.074209
[7]	BERRY M, DENNIS M. Polarization singularities in isotropic random vector waves[J]. Proceedings of the Royal Society, 2001, A457(1): 141-155.
[8]	RAJPUT R, SENTHILKUMARAN P, PAL S K. Phase singularities to polarization singularities[J]. International Journal of Optics, 2020, 1605 (1): 1-33.
[9]	PAL S K, SENTHILKUMARAN P. Hexagonal vector field of polarization singularities with a gradient basis structure[J]. Optics Letters, 2019, 44(8): 2093-2096. DOI: 10.1364/OL.44.002093
[10]	FREUND I. Polarization singularity indices in Gaussian laser beams[J]. Optics Communications, 2002, 201(4): 251-270.
[11]	YAN H W, LV B D. Evolution of emergent C-points, L-lines, and C-lines in free space[J]. Chinese Physics, 2012, B21(5): 054202.
[12]	HE D, GAO Z H, LIAN X X, et al. Composite stokes singularities in coherently and incoherently superimposed vector optical fields[J]. Optics Communications, 2012, 285(21/22): 4215-4222.
[13]	YE D H. Analysis of characteristics of Gaussian beam and its application[J]. Laser Technology, 2019, 43(1): 146-150 (in Chinese).
[14]	LI H M, ZUO J W, XU J, et al. Study on incoherent combining technology of pulsed laser beams[J]. Laser Technology, 2015, 39(2): 237-241 (in Chinese).
[15]	DUAN K L, WANG B Z, LV B D. Propagation of Hermite-Gaussian and Laguerre-Gaussian beams beyond the paraxial approximation[J]. Journal of the Optical Society of America, 2005, A22(9): 1976-80.
[16]	LI D, PENG X, PENG Y L, et al. Nonparaxial evolution of the Airy-Gaussian vortex beam in uniaxial crystal[J]. Journal of the Optical Society of America, 2017, B34(4): 891-898.
[17]	ZHANG J B, ZHOU K Z, LIANG M, et al. Nonparaxial propagation of the chirped Airy vortex beams in uniaxial crystal orthogonal to the optical axis[J]. Optics Express, 2018, 26(2): 1290-1304. DOI: 10.1364/OE.26.001290
[18]	SUN C, LV X, DENG D M, et al. Nonparaxial propagation of the radially polarized Airy-Gaussian beams with different initial launch angles in uniaxial crystals[J]. Optics Communications, 2019, 445(1): 147-157.
[19]	FREUND I, MOKHUN A I, SOSKIN M S, et al. Stokes singularity relations[J]. Optics Letters, 2002, 27(7): 545-547. DOI: 10.1364/OL.27.000545
[20]	FREUND I, SHVARTSMAN N. Wave-field phase singularities: The sign principle[J]. Physical Review, 1995, A50(6): 5164-5172.
[21]	YAN H W, LV B D. Spectral Stokes singularities of stochastic electromagnetic beams[J]. Optics Letters, 2009, 34(13): 1933-1935. DOI: 10.1364/OL.34.001933
[22]	FREUND I. Bichromatic optical Lissajous fields[J]. Optics Communications, 2003, 226(1/6): 351-376.

施引文献(1)

期刊类型引用(1)

叶东，李俊瑶，李宗辰，张颐. 基于分数涡旋光束的偏振奇点传输特性研究. 激光技术. 2024(02): 261-267 .

本站查看

其他类型引用(0)

资源附件(0)

图(5)

计量

文章访问数: 5
HTML全文浏览量: 1
PDF下载量: 5
被引次数: 1

引言
1. 理论计算
1.1 旁轴情形
1.2 非旁轴情形
2. 数值模拟
2.1 旁轴情形
2.2 非旁轴情形
3. 结论

非相干叠加光束携带C点偶极子的演化特性

作者简介:
陈海涛(1967-), 男, 博士, 教授, 现主要从事激光传输与控制的研究。E-mail: chqcht@sina.com

计量

The evolution of C-dipole by incoherent superposition beams