6061铝合金超声波辅助激光焊接变形控制研究

陈根余; 江东远; 王彬; 陈兵华; 钟沛新; 王竟如

doi:10.7510/jgjs.issn.1001-3806.2021.05.001

6061铝合金超声波辅助激光焊接变形控制研究

1.
湖南大学激光研究所，长沙 410082
2.
湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082
3.
大族激光智能装备集团有限公司，深圳 518103

基金项目:

国家重点研发计划资助项目 2018YFB1107802

详细信息

作者简介:
陈根余(1965-), 男, 博士, 教授, 博士生导师, 现主要从事激光制造及激光微细加工方面的研究。E-mail: hdgychen@163.com

中图分类号: TG456.7
计量
- 文章访问数: 10
- HTML全文浏览量: 0
- PDF下载量: 14
出版历程
- 收稿日期: 2020-10-22
- 修回日期: 2020-12-03
- 发布日期: 2021-09-24

Research on deformation control of ultrasonic-assisted laser welding of 6061 aluminum alloy

1.
Laser Research Institute, Hunan University, Changsha 410082, China
2.
State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China
3.
Han' s Laser Smart Equipment Group Co.Ltd., Shenzhen 518103, China

摘要

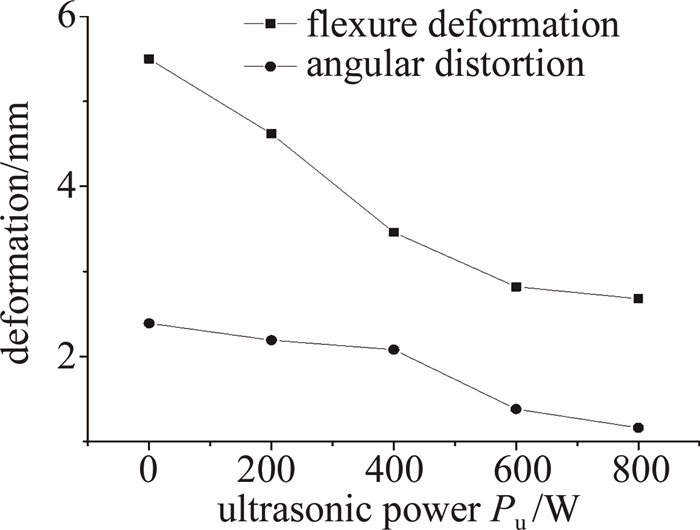
摘要: 为了解决6061铝合金在激光焊接过程中出现的易变形、变形大的问题，采用施加超声波以辅助焊接的方法，以1mm厚的6061铝合金薄板为研究对象展开超声波辅助激光焊接试验，探究超声波对6061铝合金焊接变形的抑制作用；利用单因素试验方法分析了超声波功率对焊接变形的影响规律，设计包括超声波功率、激光功率、焊接速率、离焦量、保护气流量在内的五因素五水平正交试验，分析了超声波功率以及常规焊接参量分别对焊接变形的影响程度，并获得了能够得到最小变形的工艺参量组合。结果表明，焊接变形会随着超声波功率的增加而减小，超声波功率800W时较无超声情况下试件的挠曲变形及角变形分别减小了51.27%和51.46%；同时，当激光功率为1000W、焊接速率为5m/min、离焦量为+1mm、保护气流量为15L/min、超声波功率为800W时, 可以获得变形最小的试件，所得到的试件挠曲变形量为0.42mm，角变形量为0.26mm。此研究为超声波辅助焊接在控制薄板焊接变形方面的应用提供了一定的工艺和理论参考。
- 激光技术 /
- 6061铝合金 /
- 超声波辅助激光焊接 /
- 焊接变形控制
Abstract: In order to solve the problem of easy deformation and large deformation of 6061 aluminum alloy in the laser welding process, ultrasonic assisted laser welding experiment was carried out with 1mm thick 6061 aluminum alloy sheet as the research object to explore the inhibition effect of ultrasonic on welding deformation of 6061 aluminum alloy. The influence of ultrasonic power on welding deformation was analyzed by single factor test method. Five factors and five levels orthogonal test including ultrasonic power, laser power, welding speed, defocusing amount, and shielding gas flow wer designed. The influence degree of ultrasonic power and conventional welding parameters on welding deformation was analyzed, and the process parameters combination which can obtain the minimum deformation were obtained. The results show that the welding deformation decreases with the increase of ultrasonic power, and the bending deformation and angular deformation of the specimen are reduced by 51.27% and 51.46% respectively when the ultrasonic power is 800W.At the same time, when the laser power is 1000W, the welding speed is 5m/min, the defocusing amount is + 1mm, the shielding gas flow rate is 15L/min, and the ultrasonic power is 800W, the minimum deformation of the specimen can be obtained, and the bending deformation is 0.42mm, and the angular deformation is 0.26mm. This study provides a certain technological and theoretical reference for the application of ultrasonic assisted welding in controlling welding deformation of thin plates.
- laser technique /
- 6061 aluminum alloy /
- ultrasonic assisted laser welding /
- welding deformation control

HTML全文

引言

获得高功率优质的超短脉冲光源一直是国内外光纤光学研究的热点问题。2000年, FERMANN等人^[1]首次在理论和实验上证明了带有增益的光纤放大器能够产生自相似脉冲。所谓自相似脉冲是指产生于色散渐减光纤(dispersion decreasing fiber, DDF)或光纤放大器正色散区的一类啁啾近乎线性、时域波形类似抛物线形状的渐进性脉冲。自相似脉冲具有许多优点^[2-3]：传输特性只与入射脉冲的能量和和光纤参量有关，与入射脉冲形状无关；因其产生的啁啾具有很强的线性，所以高功率传输时有抵御光波分裂的能力，能显著提升脉冲压缩的质量，故如何利用自相似脉冲来产生超短脉冲输出便成为了研究的热点^[4]。自相似脉冲的压缩方法主要采用啁啾补偿技术，常利用色散补偿光纤(dispersion compensation fiber, DCF)^[5-6]、啁啾光纤光栅^[7]等色散补偿器件或采用预啁啾处理^[8]等方法来进行啁啾补偿，其中DCF因补偿效果好、技术相对成熟且使用方便得到了广泛的应用。近年来，绝大部分的研究都主要集中在如何获取高线性啁啾的脉冲进行后期的压缩补偿，而对于补偿光纤的设计却鲜有报道。因此，本文中基于啁啾补偿技术研究自相似脉冲啁啾补偿光纤的设计，采用色散渐增光纤进行自相似脉冲的啁啾补偿。首先基于DDF产生具有强线性啁啾的自相似脉冲，进而基于啁啾特性研究自相似脉冲的后续压缩补偿问题，啁啾补偿光纤的设计采用普通色散补偿光纤以及色散渐增光纤，探讨了两种类型的压缩光纤对自相似脉冲的线性啁啾补偿效果以及高功率压缩脉冲输出性能的影响。

1. 脉冲在DDF中的自相似演化

当忽略高阶色散和非线性效应时，光脉冲在DDF中的传输可由薛定谔方程^[9-10]表示：

$\begin{gathered} \mathrm{i} \frac{\partial A(z, T)}{\partial z}=-\mathrm{i} \frac{\alpha}{2} A(z, T)+ \\ \frac{\beta_{2}}{2} D(z) \frac{\partial^{2} A(z, T)}{\partial T^{2}}-\gamma|A(z, T)|^{2} A(z, T) \end{gathered}$

(1)

式中，A(z, T)为脉冲的包络的慢变振幅，T是随脉冲以群速度移动的参考系中时间的量度，z为传输的距离，α为光纤的损耗系数，β₂为z=0时的2阶群速度色散(group velocity dispersion, GVD)参量，D(z)为色散变化参量，γ为非线性系数。当忽略光纤的损耗时，该方程便演变为以下的非线性薛定谔方程：

$\begin{gathered} \mathrm{i} \frac{\partial A(z, T)}{\partial z}=\frac{\beta_{2}}{2} D(z) \frac{\partial^{2} A(z, T)}{\partial T^{2}}- \\ \gamma|A(z, T)|^{2} A(z, T) \end{gathered}$

(2)

此时脉冲在DDF中的演化主要受2阶色散和低阶非线性影响。通过傅里叶变换，将(2)式改写为以下形式：

$\frac{\partial A(z, T)}{\partial z}=(\hat{D}+\hat{N}) A(z, T)$

(3)

式中, $\hat{D}=\frac{-\beta_{2}}{2} D(z) \frac{\partial^{2}}{\partial T^{2}}$ ，表示2阶色散作用， $\hat{N}=$ $\gamma|A(z, T)|^{2} A(z, T)$ ，表示非线性作用。由分步傅里叶方法可知，当光场通过一小段距离h时，色散和非线性效应可以分别作用。故每经过一小段距离h后的光脉冲的慢变振幅A(z+h, T)可由下式表示:

$A(z+h, T)=\exp (h \hat{D}) \exp (h \hat{N}) A(z, T)$

(4)

本文中，DDF 2阶色散随着光纤长度z以双曲型变化，即 $D(z)=\frac{1}{1+H z}$ ，其中H为增益系数，归一化D(0)=1，采用无啁啾的高斯脉冲作为输入脉冲，T₀为初始脉宽, 输入脉冲表达式为：

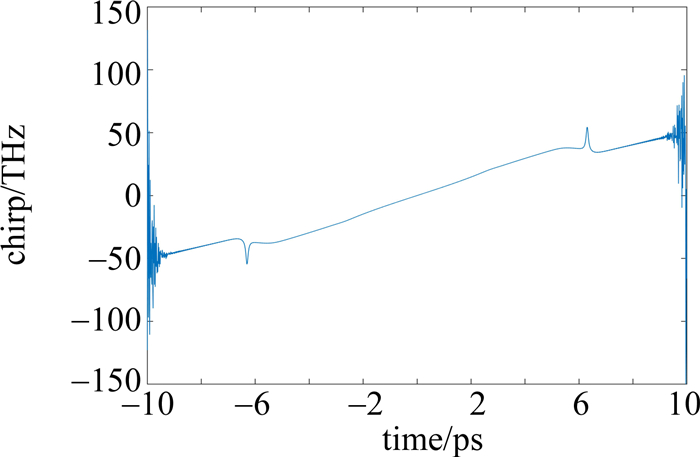
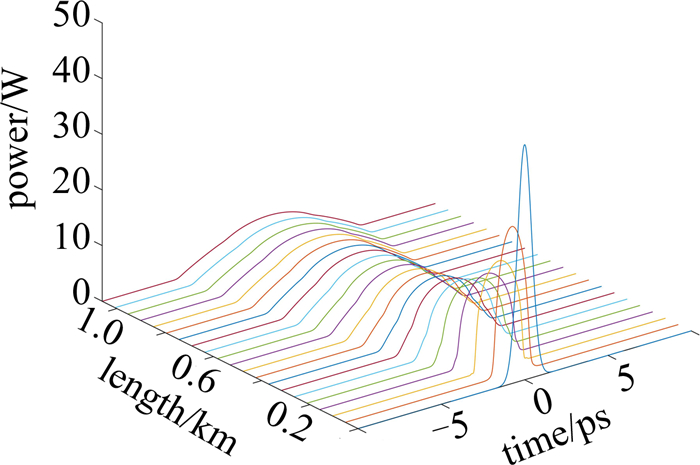
$A(0, T)=\exp \left(\frac{-T^{2}}{2 T_{0}^{2}}\right)$

(5)

初始输入高斯脉冲的半峰全宽(full width at half maximum, FWHM)T_FWHM=1ps，中心波长为1550nm，当z=0时，2阶色散系数β₂=1.36ps²/km，非线性系数γ=3.5(W·km)^-1，增益系数H=22km^-1。通过计算色散长度L_d=1.0608km，非线性长度L_NL=0.0068km，实验中设置光纤长度为4倍的色散长度L_d，此时由于光纤长度远大于非线性长度，GVD效应会对光脉冲传输起主要作用。通过前面的分步傅里叶法，可得到脉冲在DDF中不同位置的演化的数值仿真值。图 1和图 2中分别给出脉冲的时域演化趋势和输出脉冲的啁啾曲线。

Figure 1. Schematic diagram of pulse evolution in DDF

下载: 全尺寸图片幻灯片

Figure 2. Schematic diagram of output pulse chirp

下载: 全尺寸图片幻灯片

从图 1中可以看到，随着传输距离的增大，时域内脉冲不断进行展宽。其展宽的原因在传输前期主要来自于2阶GVD效应，但随着2阶GVD效应的减小，非线性效应(self-phase modulation, SPM)会逐渐变强，当GVD和SPM满足一定关系^[11]时, 就会产生具有线性啁啾的自相似脉冲，因此需要合理选择DDF的长度，保证光脉冲完成自相似演化。当光脉冲经过4倍的L_d之后，可以看到，输出脉冲的啁啾具有较大的线性范围，此时SPM效应所产生的非线性啁啾在整个脉冲范围内几乎被正常GVD效应线性化，可以认为此时脉冲已经完成了自相似演化。

2. 自相似脉冲啁啾补偿光纤设计

2.1 啁啾补偿技术理论分析

由于自相似脉冲在传输的过程中其GVD效应远大于SPM效应，因此对演化完成后的自相似脉冲进行色散补偿后，便可以对自相似脉冲进行压缩。对色散进行补偿^[11-13]的做法是在DDF后引入一段带有相反色散的光纤。对于引入相反色散光纤进行压缩脉冲可以这样理解，对于无初始啁啾的高斯脉冲在经过适当距离的DDF后，产生具有线性啁啾的自相似脉冲后在进入反常色散的光纤时，可以看作是带有啁啾的高斯脉冲，其入射场可表示为：

$U(0, T)=\exp \left[\frac{-(1+\mathrm{i} C) T^{2}}{2 T_{0}^{2}}\right]$

(6)

式中, C为线性啁啾参量，由于高斯脉冲经过了带有正常色散DDF，所以自相似脉冲感应的是正啁啾，因此啁啾参量C>0。当不考虑非线性效应时，脉冲在具有线性色散介质光纤时满足以下线性微分方程：

$\mathrm{i} \frac{\partial U(z, T)}{\partial z}=\frac{\beta_{2}}{2} \frac{\partial^{2} U(z, T)}{\partial T^{2}}$

(7)

当输入脉冲为带啁啾的高斯脉冲时，可求得上述方程的解为:

$\begin{gathered} U(z, T)=\frac{T_{0}}{\left[T_{0}^{2}-\mathrm{i} \beta_{2} z(1+\mathrm{i} C)\right]^{1 / 2}} \times \\ \exp \left\{\frac{-(1+\mathrm{i} C) T^{2}}{2\left[T_{0}^{2}-\mathrm{i} \beta_{2} z(1+\mathrm{i} C)\right]}\right\} \end{gathered}$

(8)

通过计算得到在传输距离为z时的脉冲宽度T₁与初始脉冲脉宽T₀存在以下关系：

$T_{1}=\left[\left(1+\frac{C \beta_{2} z}{T_{0}^{2}}\right)^{2}+\left(\frac{\beta_{2} z}{T_{0}^{2}}\right)^{2}\right]^{1 / 2} T_{0}$

(9)

从(9)式可以看出，若初始脉冲啁啾与光纤的2阶色散参量符号相反时，在传输适当的距离内啁啾高斯脉冲会被压缩，且存在一个最窄的压缩脉宽T₁，与光纤的2阶色散参量和长度有关。同样对于带有线性正啁啾的自相似脉冲也是一样，通过引入一段带有反常色散的光纤，在经过适当的距离后，就能够对自相似脉冲进行压缩。

2.2 普通色散补偿光纤和色散线性渐增光纤对自相似脉冲压缩的影响

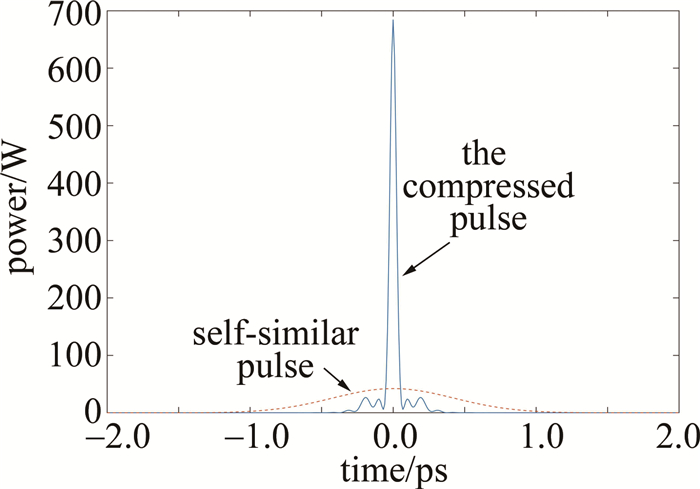
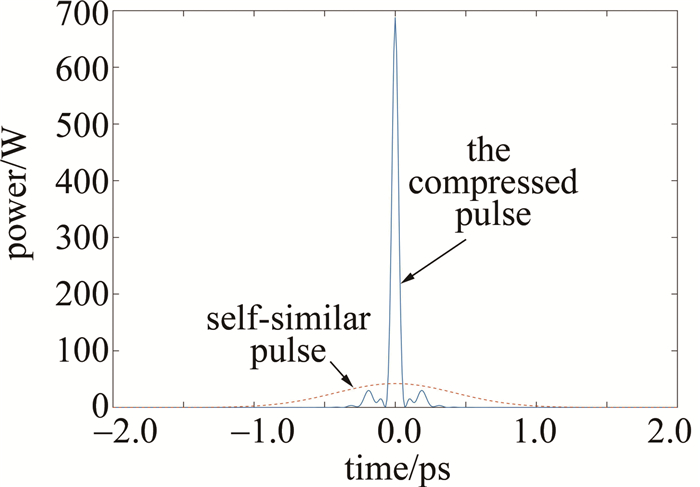
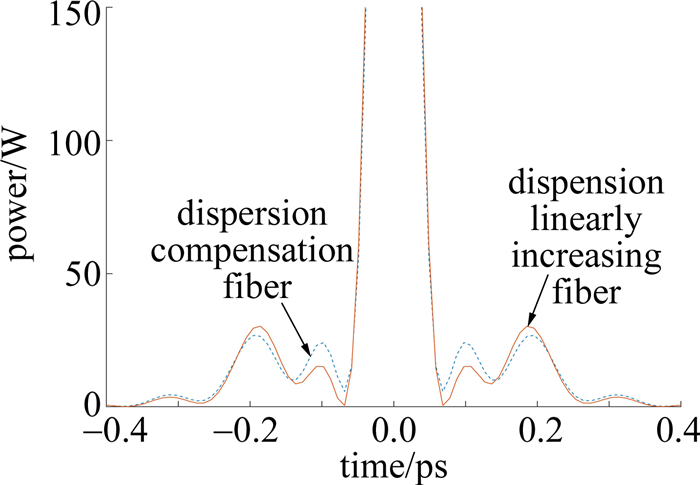
理论上,只要引入一段带有反常色散的光纤都能实现脉冲压缩的目的，因此本文中分别引入带有反常色散的色散补偿光纤(2阶色散为常量)和带有反常色散的线性渐增光纤来对自相似脉冲进行压缩，以探究不同类型的反常色散光纤对自相似脉冲的压缩影响。取色散补偿光纤的2阶色散β₂=-1.36(ps²/km)，非线性系数γ=1(W·km)^-1；色散线性渐增光纤2阶色散β₂(z)=β₂(0)(1+pz)，其中初始2阶色散系数β₂(0)=-1.36(ps²/km)，色散渐增系数p取为1km^-1，非线性系数与色散补偿光纤保持一致。通过数值仿真可以得到自相似脉冲经过各段反常色散光纤后的脉冲压缩情况。图 3和图 4分别为自相似脉冲经过普通色散补偿光纤和色散线性渐增光纤的压缩示意图，图 5为自相似脉冲经过色散补偿和色散线性渐增光纤脉冲后的压缩对比图。

Figure 3. Schematic diagram of pulse compression of ordinary dispersion compensation fiber

下载: 全尺寸图片幻灯片

Figure 4. Schematic diagram of pulse compression for linearly increasing dispersion fiber

下载: 全尺寸图片幻灯片

Figure 5. Partial enlarged view of pulse compression of dispersion compensation fiber and linearly increasing dispersion fiber

下载: 全尺寸图片幻灯片

通过数值仿真，当获得最佳超短脉冲输出时，色散补偿光纤长度为97.8m，超短输出脉冲半峰全宽T_FWHM=52.6fs，输出脉冲峰值功率为684.5W；而色散线性渐增光纤长度为93.0m，超短输出脉冲半峰全宽T_FWHM=53.8fs，输出脉冲峰值功率为688.2W。可以看到, 当色散渐增系数p=1km^-1时，色散线性渐增光纤与色散补偿光纤一样能将自相似脉冲压缩至50fs量级，但色散线性渐增光纤与色散补偿光纤所产生的脉冲基座略有不同，色散线性渐增光纤的基座波动相对较小，且色散线性渐增光纤的光纤长度也小于色散补偿光纤。因此，相比较于普通色散补偿光纤，色散线性渐增光纤能获取较高质量的自相似脉冲压缩。

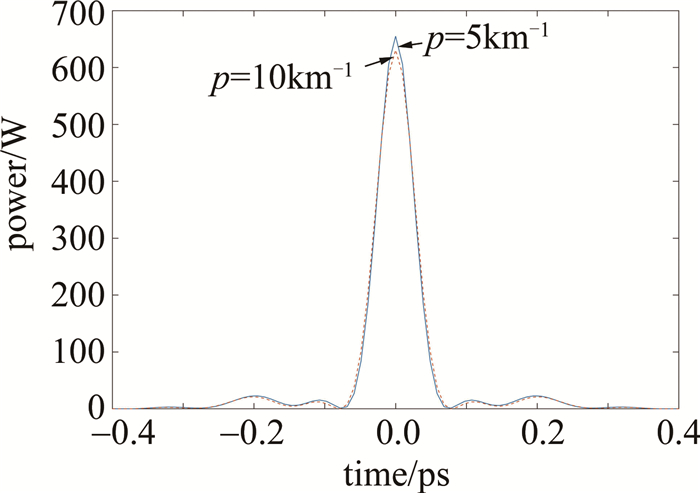
为了进一步探究色散渐增系数p对压缩质量的影响，在保持其它参量不变的情况下改变p值，观察脉冲在色散线性渐增光纤中的演化情况。图 6是p为5km^-1和10km^-1时的最佳超短脉冲输出示意图。

Figure 6. Schematic diagram of pulse compression of fibers with linearly increasing dispersion at p=5km^-1, 10km^-1

下载: 全尺寸图片幻灯片

表 1为自相似脉冲经过不同p值的色散线性渐增光纤后输出最短脉冲的数值模拟值。通过数值仿真可知，当p=5km^-1时，压缩至最短脉冲所需的光纤长度缩短为81.0m，最短脉冲半峰全宽T_FWHM=58.0fs; 当p=10km^-1时，所需的光纤长度缩短为74.2m，最短脉冲半峰全宽T_FWHM=61.8fs。由以上结果可以得出：当保持光纤其它参量不变时，增大色散线性渐增系数p可以明显缩短超短脉冲输出时的补偿光纤长度，有利于减小脉冲在传输过程中产生的损耗，从而有效提高自相似脉冲的压缩质量，但随着色散渐增系数p迅速提高，其输出脉冲的峰值功率和脉宽也会略微有所降低。最终在p=10km^-1时获得功率为630.6W、脉宽为61.8fs的超短脉冲输出。

Table 1. Numerical simulation results of fibers with linearly increasing dispersion

	p=1km^-1	p=5km^-1	p=10km^-1
optimal compensation fiber length/m	93.0	81.0	74.2
full width at half maximum of ultrashort pulse output/fs	53.8	58.0	61.8
peak power of output pulse/W	688.2	655.1	630.6

下载: 导出CSV

| 显示表格

2.3 色散指数渐增光纤对自相似脉冲压缩的影响

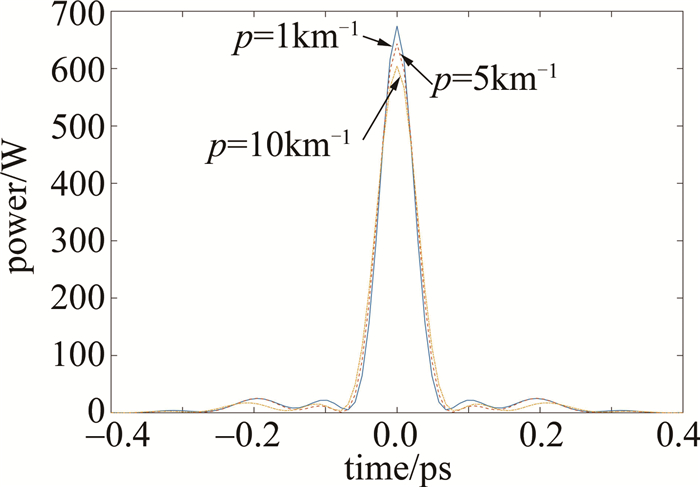
为了验证其它类型的色散渐增光纤是否也有类似的规律，又引入了色散指数渐增光纤来压缩自相似脉冲。色散指数渐增光纤的2阶色散可以表示为：β₂(z)=β₂(0)exp(pz)，其中初始2阶色散系数β₂(0)=-1.36(ps²/km)，与色散线性渐增光纤一样分别取p为1km^-1，5km^-1，10km^-1，非线性系数与上述光纤保持一致，通过数值仿真得出自相似脉冲在色散指数渐增光纤中的演化结果。图 7是p分别为1km^-1，5km^-1，10km^-1时色散指数渐增光纤的脉冲压缩示意图。

Figure 7. Schematic diagram of pulse compression of fiber with increasing dispersion index at p=1km^-1, 5km^-1, 10km^-1

下载: 全尺寸图片幻灯片

表 2为自相似脉冲经过不同p值的色散指数渐增光纤后输出最短脉冲的数值模拟值。当色散渐增系数p=1km^-1时，压缩至最短脉冲所需的色散指数渐增光纤长度为92.5m，最短脉冲半峰全宽T_FWHM=54.2fs，输出脉冲峰值功率为674.2W；当色散渐增系数p=5km^-1时，压缩至最短脉冲所需的光纤长度为82.5m，最短脉冲半峰全宽T_FWHM=59.4fs，输出脉冲峰值功率为643.3W；当色散渐增系数p=10km^-1时，压缩至最短脉冲所需的光纤长度缩短为70.3m，最短脉冲半峰全宽T_FWHM=64.4fs，输出脉冲峰值功率为604.4W。

Table 2. Numerical simulation results of fibers with increasing dispersion index

	p=1km^-1	p=5km^-1	p=10km^-1
optimal compensation fiber length/m	92.5	82.5	70.3
full width at half maximum of ultrashort pulse output/fs	54.2	59.4	64.4
peak power of output pulse/W	674.2	643.3	604.4

下载: 导出CSV

| 显示表格

上述结果与利用色散线性渐增光纤压缩脉冲得出的结论不谋而合，因此可以认为: 当保持其它参量不变时，增大色散渐增系数，能有效地缩短脉冲压缩所需的补偿光纤长度，在实际的光纤线路中，缩短补偿光纤长度就意味着能避免更多的损耗，从而提高脉冲的压缩质量，得到高质量的超短脉冲输出，但随着色散渐增系数的迅速增加，输出功率和脉宽也会略微减小，因此需要合理地选择色散渐增系数，在保证脉冲压缩质量的前提下缩短压缩光纤的长度。同时, 在比较指数型色散渐增光纤和线性型色散渐增光纤时可以发现，当色散渐增系数相等时，线性型色散渐增光纤的压缩效果要比指数型色散渐增光纤的压缩效果好。

3. 结论

利用DDF产生了具有线性啁啾的自相似脉冲，采用啁啾补偿技术进行了自相似脉冲压缩。输入半峰全宽T_FWHM=1ps、峰值功率为42W的高斯脉冲，经过DDF后形成带有线性啁啾的自相似脉冲，随后又通过长度为97.8m的普通色散补偿光纤后得到半峰全宽T_FWHM=52.6fs、峰值功率为684.5W的超短脉冲输出。在此基础上，讨论了色散线性渐增光纤和色散指数渐增光纤对压缩脉冲的影响，当自相似脉冲通过色散渐增系数p=1km^-1、长度为93.0m的色散线性渐增光纤后得到半峰全宽T_FWHM=53.8fs、峰值功率为688.2W的超短脉冲输出；通过色散渐增系数p=5km^-1、长度为81.0m的色散线性渐增光纤后得到半峰全宽T_FWHM=58.0fs、峰值功率为655.1W的超短脉冲输出；通过色散渐增系数p=10km^-1、长度为74.2m的色散线性渐增光纤后得到半峰全宽T_FWHM=61.8fs、峰值功率为630.6W的超短脉冲输出。当自相似脉冲通过色散渐增系数p=1km^-1、长度为92.5m的色散指数渐增光纤后，得到半峰全宽T_FWHM=54.2fs、峰值功率为674.2W的超短脉冲输出；通过色散渐增系数p=5km^-1、长度为82.5m的色散指数渐增光纤后，得到半峰全宽T_FWHM=59.4fs、峰值功率为643.3W的超短脉冲输出；通过色散渐增系数p=10km^-1、长度为70.3m的色散指数渐增光纤后，得到半峰全宽T_FWHM=64.4fs、峰值功率为604.4W的超短脉冲输出。结果表明, 利用色散渐增光纤作为啁啾补偿光纤能明显缩短补偿光纤的长度，在保证其它参量不变的情况下，增大色散渐增系数会进一步缩短脉冲压缩所需的光纤长度，但随着色散渐增系数的迅速增加，输出功率和脉宽也会略微减小。

Figure 1. Ultrasonic assisted laser welding system

下载: 全尺寸图片幻灯片

Figure 2. Influence of ultrasonic power on welding deformation

下载: 全尺寸图片幻灯片

Figure 3. Single factor experiment results of ultrasonic power

下载: 全尺寸图片幻灯片

Figure 4. Specimen with minimum deformation

下载: 全尺寸图片幻灯片

Figure 5. Effect of ultrasonic power on tensile strength of specimens

下载: 全尺寸图片幻灯片

Figure 6. Weld front morphology of unqualified test piece

a—No.3 test piece b—No.1 test piece

下载: 全尺寸图片幻灯片

Table 1 Mass fraction table of chemical composition of 6061 aluminum alloy

material	Si	Fe	Cu	Mg	Mn	Cr	Zn	Ti	Al
6061	0.004	0.007	0.0015	0.006~0.012	0.0015	0.0005~0.0035	0.0025	0.001	margin

下载: 导出CSV

Table 2 Single factor experiment parameters

processing parameters	value
ultrasonic power P_u	0W, 200W, 400W, 600W, 800W
laser power P	1200W
defocus amount Δ	0mm
welding speed v	4m/min
shielding gas flow rate Q₁	10L/min
blowing angle of shielding gas	45°
back gas flow rate Q₂	10L/min

下载: 导出CSV

表 3 Orthogonal experiment parameters

experimental factor	laser power P/W	welding speed v /(mm·s^-1)	defocus amount Δ/mm	shielding gas flow rate Q₁/(L·min^-1)	ultrasonic power P_u/W
level 1	1000	2	-2	0	0
level 2	1100	3	-1	5	200
level 3	1200	4	0	10	400
level 4	1300	5	1	15	600
level 5	1400	6	2	20	800

下载: 导出CSV

表 4 Result of orthogonal experiment

level	factor A	factor B	factor C	factor D	factor E	flexure deformation/mm	angular deformation/mm
level	laser power P/W	welding speed v/(m·min^-1)	defocus amount Δ/mm	shielding gas flow rate Q/(L·min^-1)	ultrasonic power P_u/W	flexure deformation/mm	angular deformation/mm
1	1000	6	2	20	400	0.80	0.36
2	1000	2	-2	0	0	2.52	1.82
3	1000	5	1	15	800	0.42	0.26
4	1000	4	0	10	200	1.59	0.47
5	1000	3	-1	5	600	2.00	1.08
6	1100	3	2	0	400	3.31	1.74
7	1100	2	1	20	600	2.32	1.14
8	1100	6	0	15	0	0.78	0.47
9	1100	5	-1	10	200	1.58	0.56
10	1100	4	-2	5	800	1.74	0.70
11	1200	5	2	5	0	2.02	1.26
12	1200	3	0	20	800	1.92	0.87
13	1200	2	-1	15	400	3.02	2.00
14	1200	4	1	0	200	2.62	0.84
15	1200	6	-2	10	600	0.72	0.40
16	1300	2	2	10	800	3.46	1.35
17	1300	3	-2	15	200	3.68	1.60
18	1300	5	0	0	600	1.18	0.48
19	1300	4	-1	20	0	1.54	1.02
20	1300	6	1	5	400	0.88	0.32
21	1400	6	-1	0	800	0.54	0.42
22	1400	3	1	10	0	2.70	1.56
23	1400	4	2	15	600	2.20	1.53
24	1400	2	0	5	400	3.43	2.10
25	1400	5	-2	20	200	1.37	0.90

下载: 导出CSV

Table 5 Analysis of orthogonal test results

	summation and range of factor A/mm	summation and range of factor B/mm	summation and range of factor C/mm	summation and range of factor D/mm	summation and range of factor E/mm
T_i1	7.33	14.75	11.79	10.17	9.56
T_i2	9.73	13.61	8.94	10.07	10.84
T_i3	10.30	9.69	8.90	10.05	11.44
T_i4	10.74	6.57	8.68	10.10	8.42
T_i5	10.24	3.72	10.03	7.95	8.08
R_T	3.41	11.03	1.35	2.22	3.36
S_i1	3.99	8.41	6.24	5.30	6.13
S_i2	4.61	6.85	4.12	5.46	4.29
S_i3	5.37	4.56	4.39	4.34	6.48
S_i4	4.77	3.46	5.08	5.86	4.63
S_i5	6.51	1.97	5.42	4.29	3.60
R_S	2.52	6.44	2.12	1.57	2.92

下载: 导出CSV

Table 6 Experimental results of theoretical optimal process parameters

experimental factor	laser power/ W	welding speed/ (m·min^-1)	defocus amount/ mm	shielding gas flow rate/(L·min^-1)	ultrasonic power/ W	flexure deformation/ mm	angular distortion/ mm
1	1000	6	-1	20	800	0.50	0.33
2	1000	6	+1	20	800	0.58	0.30

下载: 导出CSV

Table 7 ISO 15614-2-2005 application standard of tensile strength for different groups of aluminum alloy

material group	temper condition of parent material before welding	post weld condition	φ
21	all temper condition	as welded	1
22	all temper condition	as welded	1
23.1	T4	natural ageing	0.7
	T4	artificial ageing	0.7
	T5/T6	natural ageing	0.6
	T5/T6	artificial ageing	0.7
23.2	T4	natural ageing	0.95
	T4	artificial ageing	0.75
	T6	natural ageing	0.75
	T6	artificial ageing	0.75

下载: 导出CSV

表 8 ISO/TR 15608:2017 grouping system for aluminum and aluminum alloys

group	subgroup	type of aluminum and aluminum alloy
21		pure aluminum with w≤0.01 impurities or alloy content
22		non heat treatable alloys
	22.1	aluminum-manganese alloys
	22.2	aluminum-magnesium alloys with w(Mg)≤0.015
	22.3	aluminum-magnesium alloys with 0.015＜w(Mg)≤0.035
	22.4	aluminum-magnesium alloys with w(Mg)＞0.035
23		heat treatable alloys
	23.1	Al-Mg-Si alloys
	23.2	Al-Zn-Mg alloys
24	24.1	aluminum-silicon alloys with w(Cu)≤0.01
	24.1	aluminum-silicon alloys with w(Cu)≤0.01 and 0.05＜w(Si)≤0.15
	24.2	aluminum-silicon-magnesium alloys with w(Cu)≤ 0.01；0.05＜w(Si)≤0.15 and 0.001＜w(Mg)≤0.008
25		aluminum-silicon-copper alloys with 0.05＜w(Si)≤0.14；0.01＜w(Cu)≤0.05 and w(Mg)≤0.008
26		aluminum-copper alloys with 0.02＜w(Cu)≤0.06

下载: 导出CSV

Table 9 Results of tensile strength of specimens with small deformation

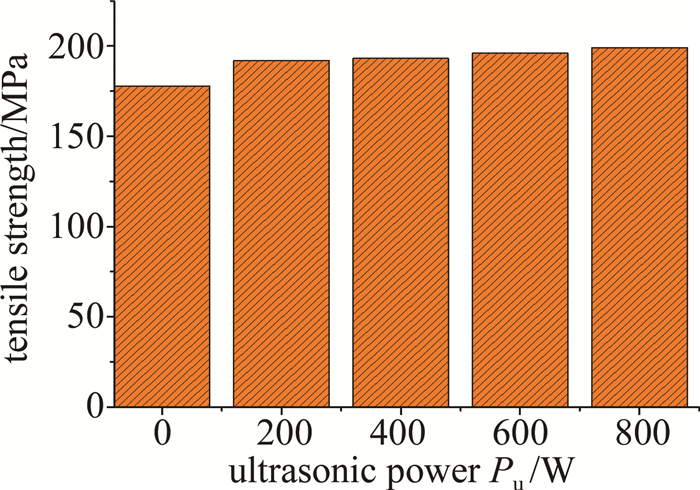
experimental factor	tensile strength/MPa
3	154.35
21	189.78
15	175.39
8	168.64
1	162.56

下载: 导出CSV

参考文献(21)

[1]	LIN J B. Aluminum alloy welding technology research[J]. World Nonferrous Metals, 2017(8): 76-78(in Chinese).
[2]	ZHANG W, YE B, QI X Y, et al. Study on the effect of energy ratio in laser-MIG hybrid welding of 6061 aluminium alloy[J]. Laser Technology, 2018, 42(4): 500-504(in Chinese). http://www.zhangqiaokeyan.com/academic-journal-cn_laser-technology_thesis/0201236224441.html
[3]	WANG X H, GU X Y, SUN D Q. Research on interface characteristic of laser welding joints of steel/aluminum dissimilar materials[J]. Journal of Mechanical Engineering, 2017, 53(4): 26-33(in Chinese). DOI: 10.3901/JME.2017.04.026
[4]	LEI Z, LI Y, CHEN Y, et al. Effect of process parameters on porosity formation ratio in dual-beam laser welding of aluminum alloys with filler wire[J]. Transactions of the China Welding Institution, 2013, 34(2): 40-44. http://en.cnki.com.cn/Article_en/CJFDTOTAL-HJXB201302009.htm
[5]	SU Sh X, YU Y L, FEI W, et al. Research of characteristics of weld formation of aluminum alloy by high power fiber laser welding[J]. Laser Technology, 2017, 41(3): 322-327(in Chinese).
[6]	YE H Y, HE J, CAI J P, et al. Welding deformations of 6061-T651 Al alloy thin-plate joints[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2435-2442(in Chinese).
[7]	LI Sh L, MA Y J, WANG D Y, et al. Influence of welding with trailing peening on welding stress based on electromagnetism control[J]. Welding Technology, 2008, 37(4): 66-68(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-HSJJ200804026.htm
[8]	HE X M, WANG Y M, ZHANG C H. Influence of high energy shot peening on microstructure and properties of TC4 welded joints[J]. Transactions of the China Welding Institution, 2016, 37(6): 40-44(in Chinese). http://www.researchgate.net/publication/305540076_Influence_of_high_energy_shot_peening_on_microstructure_and_properties_of_TC4_welded_joints
[9]	LI J Y, LU Y M, LIU Z P, et al. Residual stresses and distortions in aluminum alloy sheet after welding under pre-tension[J]. Materials Science Forum, 2009, 618/619: 45-48. DOI: 10.4028/www.scientific.net/MSF.618-619.45
[10]	LIU X D, TAO X H, HAN Zh Q. Application of vibratory stress relief in relaxation of residual stress for expandable corrugated liners[J]. Journal of Vibration and Shock, 2015, 34(4): 171-174(in Chinese). http://www.cqvip.com/QK/95775X/201504/663694356.html
[11]	JI P, JI H. Study on welding residual stress and welding deformation control of steel structure[J]. World Nonferrous Metals, 2017(3): 191-193(in Chinese).
[12]	JIANG Y F, DING B, CHENG Zh J, et al. Effect of laser peening area on residual stress field in small-hole specimens[J]. Laser Technology, 2014, 38(2): 201-204(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201402012.htm
[13]	LI Zh, LIU J, BAI Ch M, et al. Study on effect of ultrasonic on laser-arc hybrid welding of aluminum alloy[J]. Laser Technology, 2019, 43(3): 301-306(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-JGJS201903003.htm
[14]	LIU H D, HU F Y, LI H B, et al. Classification research and the application summarization of power ultrasonic technology[J]. Electric Welding Machine, 2014, 44(12): 31-35(in Chinese). http://www.zhangqiaokeyan.com/academic-journal-cn_electric-welding-machine_thesis/0201228766474.html
[15]	ZHAO Zh Q, YAN X, LI D, et al. Effect of the front trailing ultrasonic impact treatment on welding residual stress and deformation[J]. Electric Welding Machine, 2019, 49(5): 79-83(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTotal-DHJI201905016.htm
[16]	GE H L. Study on microstructure of weld joint of aluminum alloy and research of mechanism of ultrasonic impact[D]. Harbin Institute of Technology, 2016: 17-30(in Chinese).
[17]	GAO S, WU C S, PADHY G K. Material flow, microstructure and mechanical properties of friction stir welded AA 2024-T3 enhanced by ultrasonic vibrations[J]. Journal of Manufacturing Processes, 2017, 30: 385-395. DOI: 10.1016/j.jmapro.2017.10.008
[18]	LI S H. Effect of real time ultrasonic impact treatment on welding residual stress, deformation and microstructure property[D]. Haerbin: Harbin Institute of Technology, 2014: 32-44(in Chinese).
[19]	HUANG H H. Study on controlling of welding stress and distortion for aluminum alloy by welding with trailing ultrasonic vibration[D]. Quanzhou: Huaqiao University, 2014: 50-56(in Chinese).
[20]	LIU Y, SHEN N J. Residual stresses analysis for actual material model of autofrettaged tube by non-linear boundary element method[J]. Elsevier, 1991, 48(1): 10-25.
[21]	LIU X X. Study on the control of laser welding deformation of titanium alloy thin sheet[D]. Changsha: Hunan University, 2014: 9-11(in Chinese).

施引文献(1)

期刊类型引用(1)

庞亮雨，张巧芬，高梓皓，陈楚浜，吴铭扬. 基于Mach-Zehnder干涉仪的自相似激光器压缩系统设计. 激光技术. 2023(06): 803-810 .

本站查看

其他类型引用(0)

资源附件(0)

图(6) / 表(9)

计量

文章访问数: 10
HTML全文浏览量: 0
PDF下载量: 14
被引次数: 1

引言
1. 脉冲在DDF中的自相似演化
2. 自相似脉冲啁啾补偿光纤设计
2.1 啁啾补偿技术理论分析
2.2 普通色散补偿光纤和色散线性渐增光纤对自相似脉冲压缩的影响
2.3 色散指数渐增光纤对自相似脉冲压缩的影响
3. 结论

6061铝合金超声波辅助激光焊接变形控制研究

作者简介:
陈根余(1965-), 男, 博士, 教授, 博士生导师, 现主要从事激光制造及激光微细加工方面的研究。E-mail: hdgychen@163.com

计量

Research on deformation control of ultrasonic-assisted laser welding of 6061 aluminum alloy