Investigation on characteristics of 3-D function photonic crystal
-
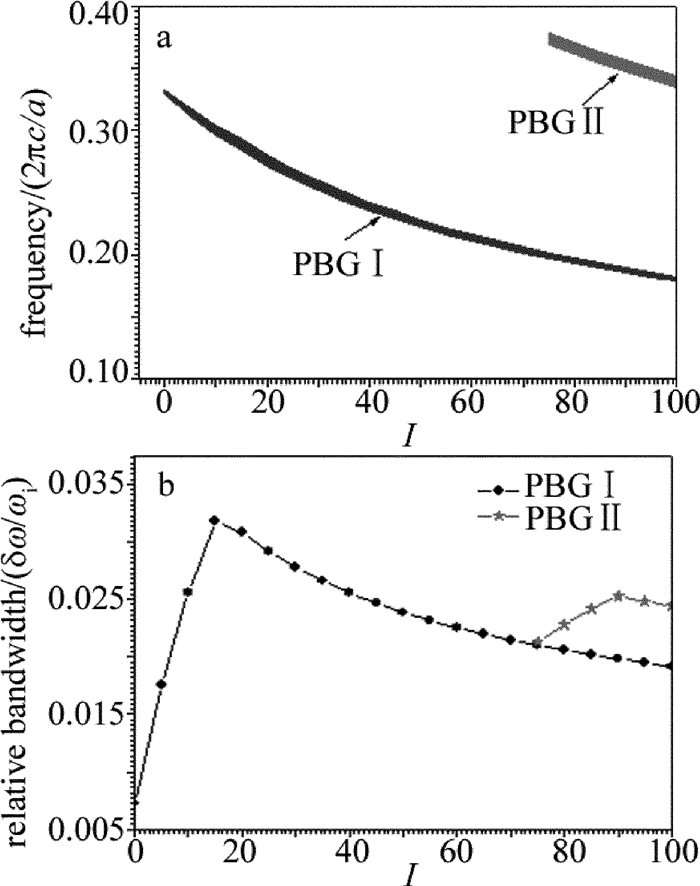
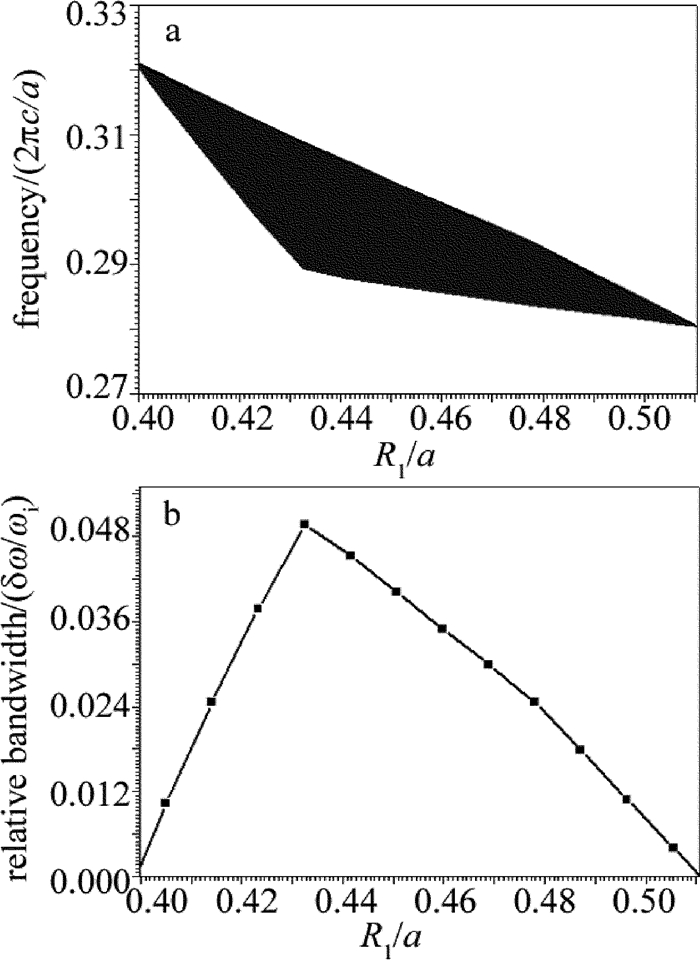
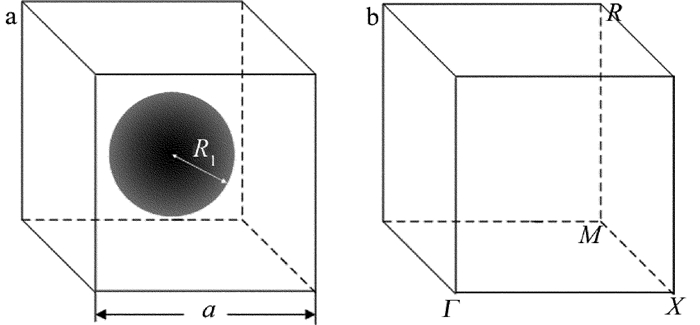
摘要: 为了研究3维函数光子晶体的光子禁带特性，采用平面波展开法计算得到色散曲线，推导了平面波展开法的相关计算公式以及介质球介电常数的函数关系式，探讨了可调参量函数系数I和介质球半径R1对光子禁带特性的影响。结果表明，3维函数光子晶体呈立方体晶格分布，由介质球填充空气背景；与常规3维介质光子晶体相比，3维函数光子晶体不仅能得到可调谐的光子禁带，而且可以拓展禁带带宽，并增加光子禁带的数量；改变函数系数I的大小可以实现对光子禁带数量、位置和带宽的调谐；改变介质球半径R1可以对光子禁带带宽实现展宽，并改变光子禁带的位置。该研究对设计新型可调谐器件是有帮助的。Abstract: In order to study photonic band gap of 3-D functional photonic crystal, dispersion curve was calculated by using plane wave expansion method. Correlation calculation formula of plane wave expansion method and function relation of dielectric constant of dielectric sphere were derived. The effects of the adjustable parameter I and dielectric sphere radius R1 on photonic band gap were discussed. The result shows that, 3-D function photonic crystal is cube lattice distribution and air background is filled with medium ball. Compared with conventional 3-D dielectric photonic crystals, 3-D function photonic crystal can obtain the tunable photonic band gap, expand the bandwidth of forbidden band, and increase the number of photonic band gaps. The number, position and bandwidth of photonic band gaps can be tuned by changing the size of tunable parameter I. At the same time, the bandwidth and position of photonic band gaps can be tuned by changing the sphere radius R1 of the medium. The study is helpful for the design of new tunable devices.
-
-
![]()
Figure 1. a—schematic structure of unit cell of 3-D function photonic crystal b—the first irreducible Brillouin zone of the unit cell
![]()
Figure 3. Dispersion curves of 3-D function photonic crystal with different I
a—I=-5 b—I=15 c—I=75 d—I=90
![]()
Figure 4. a—relationship between parameter I and frequency of PBGs b—relationship between parameter I and relative bandwidths of PBGs
-
[1] JOHN S. Strong localization of photons in certain disordered dielectric superlattices[J]. Physical Review Letters, 1987, 58(23):2486-2490. DOI: 10.1103/PhysRevLett.58.2486
[2] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Physical Review Letters, 1987, 58(20):2059-2062. DOI: 10.1103/PhysRevLett.58.2059
[3] ZHANG H F. Study on electromagnetic characteristics of plasma photonic crystals[D].Nanjing: Nanjing University of Aeronautics and Astronautics University, 2014: 14-31(in Chinese).
[4] RYBIN M V, KHANIKAEV A B, INOUE M, et al. Fano resonance between Mie and Bragg scattering in photonic crystals[J]. Physical Review Letters, 2009, 103(2):023901. DOI: 10.1103/PhysRevLett.103.023901
[5] WANG Z, FAN S. Compact all-pass filters in photonic crystals as the building block for high-capacity optical delay lines[J]. Physical Review, 2003, E68(6):066616. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c28b2654ab16f9f5cc3f8d9650052de4
[6] ZHANG H F, LIU S B. Enhanced the tunable omnidirectional photonic band gaps in the two-dimensional plasma photonic crystals[J]. Optical and Quantum Electronics, 2016, 48(11):508-511. DOI: 10.1007/s11082-016-0782-9
[7] LIU Q, LI S, GAO X, et al. Simulation of a short and broadband polarization splitter based on photonic crystal fiber filled with tellurite glass[J]. Optical and Quantum Electronics, 2017, 49(2):60-64. DOI: 10.1007/s11082-017-0896-8
[8] MA R K, ZHANG Y Ch, FANG Y T. Broadband THz absorbers based on graphene and 1-D photonic crystal[J]. Laser Technology, 2017, 41(5):723-727(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201705021
[9] LI Y, MO W Ch, YANG Zh G, et al. Generation of terahertz vortex beams base on metasurface antenna array[J]. Laser Technology, 2017, 41(5):644-648(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201705005
[10] CHAU Y F, YANG T J, LEE W D. Coupling technique for efficient interfacing between silica waveguides and planar photonic crystal circuits[J]. Applied Optics, 2004, 43(36):6656-6663. DOI: 10.1364/AO.43.006656
[11] ZHANG H F, LIU S B. The tunable omnidirectional reflector based on two-dimensional photonic crystals with superconductor constituents[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2015, 21(2):1-8. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6893028
[12] WANG Y, ZHANG D, XU S, et al. Low-loss Y-junction two-dimensional magneto-photonic crystals circulator using a ferrite cylinder[J]. Optics Communications, 2016, 369:1-6. DOI: 10.1016/j.optcom.2016.02.019
[13] ZHANG H F, LIU S B. Analyzing the photonic band gaps in two-dimensional plasma photonic crystals with fractal Sierpinski gasket structure based on the Monte Carlo method[J]. AIP Advances, 2016, 6(8):085116. DOI: 10.1063/1.4961726
[14] NORRIS D J, VLASOV Y A. Chemical approaches to three-dimensional semiconductor photonic crystals[J]. Advanced materials, 2001, 13(6):371-376. DOI: 10.1002/(ISSN)1521-4095
[15] PIPER J R, FAN S. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided re-sonance[J]. ACS Photonics, 2014, 1(4):347-353. DOI: 10.1021/ph400090p
[16] XIAO L, LEI T Y, LIANG Y, et al. Two-dimensional function photonic crystal.Acta Physica Sinica, 2016, 65(13):134207(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/zgjg-e200804015
[17] LIU X J, LIANG Y, MA J, et al. Two-dimensional function photonic crystals[J]. Physica, 2017, E85:227-237. http://d.old.wanfangdata.com.cn/Periodical/jldxzrkxxb201704037
[18] WU X Y, ZHANG B J, YANG J H, et al. Transmission character of general function photonic crystals[J]. Physica, 2012, E45:166-172. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1205.1178
[19] LUO M, LIU Q H. Three-dimensional dispersive metallic photonic crystals with a bandgap and a high cutoff frequency[J]. Journal of the Optical Society of America, 2010, A27(8):1878-1884. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=91a87df8f7e677711d04db37f1d42b89
[20] ZHANG H F, LIU S, KONG X K. Properties of anisotropic photonic band gaps in three-dimensional plasma photonic crystals containing the uniaxial material with different lattices[J]. Progress in Electromagnetics Research, 2013, 141:267-289. DOI: 10.2528/PIER13051703
[21] ZHANG H F, DING G W, LI H M, et al. Complete photonic band gaps and tunable self-collimation in the two-dimensional plasma photonic crystals with a new structure[J]. Physics of Plasmas, 2015, 22(2):022105. DOI: 10.1063/1.4906886
[22] ZHANG H F, CHEN Y Q. The properties of two-dimensional fractal plasma photonic crystals with Thue-Morse sequence[J]. Physics of Plasmas, 2017, 24(4):042116. DOI: 10.1063/1.4981220
[23] HO K M, CHAN C T, SOUKOULIS C M. Existence of a photonic gap in periodic dielectric structures[J]. Physical Review Letters, 1990, 65(25):3152-3155. DOI: 10.1103/PhysRevLett.65.3152
[24] LI L. Use of Fourier series in the analysis of discontinuous periodic structures[J]. Journal of the Optical Society of America, 1996, A13(9):1870-1876. DOI: 10.1364-JOSAA.13.001870/
[25] ZHANG H F, LIU S B, KONG X K, et al. The characteristics of photonic band gaps for three-dimensional unmagnetized dielectric plasma photonic crystals with simple-cubic lattice[J]. Optics Communications, 2013, 288:82-90. DOI: 10.1016/j.optcom.2012.09.078
-
期刊类型引用(1)
1. 张浩，马宇，章海锋，杨靖，刘佳轩. 一种带宽展宽的等离子体超材料吸波体的设计. 激光技术. 2019(02): 256-262 . 
本站查看
其他类型引用(2)
下载:
计量
- 文章访问数: 10
- HTML全文浏览量: 0
- PDF下载量: 5
- 被引次数: 3