网站地图
下载:
-
拉盖尔-高斯光束是涡旋光束的重要组成部分[1]。实验中常见的涡旋光束形式主要包括：非简并的拉盖尔-高斯(Laguerre-Gaussian, LG)光束、环形涡旋光束以及高阶贝塞尔光束等[2]。涡旋光束具有暗中空、螺旋形相位波前和轨道角动量传输不变的特性[3]，在微操纵、原子光学、材料科学、信息传输、生物医学等领域显示出巨大的前景[4]。如何高效地获得高纯度、高质量的激光模式一直是研究的热点和难点[5]。
获得拉盖尔-高斯模式的方法主要有衍射光栅法、螺旋相位板法、计算机全息图法等。其中计算机全息图法具有方案简单、输出纯度高的优势。空间光调制器凭借其可实现滤波，输出光束动态可控等特点在计算机全息图法中应用广泛。
本文中设计了一套基于相位型空间光调制器产生不同阶拉盖尔-高斯光束的实验装置，通过对拉盖尔-高斯模拟图的修正，得到可用于空间光调制器的二进制全息图。利用小孔光阑进行模式选择，实现了不同阶拉盖尔-高斯模式的输出。本文中提出的基于空间光调制器的方法结构简单、成本低廉，并可实现动态可控的光束输出，对于高效产生涡旋光束以及光镊的发展具有重要意义。
-
拉盖尔-高斯模式和厄米-高斯模式一样，是在开式光腔条件下，由菲涅耳-基尔霍夫方程得出的谐振腔中两种最基本的激光模式。拉盖尔-高斯模式是在圆柱坐标系下表征的，而厄米-高斯模式是在笛卡尔坐标系下表征的，这两种模式常见的表示方法为LGpl和HGmn。对于厄米-高斯模式，m和n分别是沿x和y方向的节点数。对于拉盖尔-高斯模式，l表示相位沿圆周方向旋转的圈数，p表示径向节点数。拉盖尔-高斯模式在圆柱坐标下的振幅表示为[6]：
$ \begin{array}{l} {u_{p, l}}(r, \varphi , , z) = {{\rm{e}}^{ - {\rm{i}}k{r^2}/(2R)}}{{\rm{e}}^{ - {r^2}/{w^2}}}{{\rm{e}}^{ - {\rm{i}}(2p + l + 1)\psi }} \times \\ \;\;\;\;\;\;{{\rm{e}}^{ - {\rm{i}}l\varphi }}{( - 1)^p}{(\sqrt 2 r/w)^l}{{\rm{L}}_{p, l}}(2{r^2}/{w^2}) \end{array} $
(1) 式中，r, φ, z分别表示椭圆柱坐标系下的3个维度; R表示波前的曲率半径; w表示高斯光场振幅值下降到其轴上值1/e处的光斑半径; ψ表示Gouy相位[7]; Lp，l表示广义拉盖尔多项式。其中的方位角分量，即e-ilφ项是厄米-高斯模式和拉盖尔-高斯模式的区别所在。这个相位项使得拉盖尔-高斯模式具有螺旋的相位波前。
-
任何周期性的结构都可以等效于一个衍射光栅，利用空间光调制器基元的二态性，可以用其模拟一个光栅，从而实现对于入射光场振幅和相位的调制。而此时的空间光调制器，实际上可以等效为一个从入射光到出射光的传递函数。
假设在输出平面得到拉盖尔-高斯光场，只需使通过空间光调制器的光满足拉盖尔-高斯光束的傅里叶变换即可，根据通过空间光调制器前后光束的表达式，可以计算出空间光调制器的透过率函数，这样就实现了通过控制空间光调制器的调制模式实现不同的拉盖尔-高斯模式输出。
由于液晶空间光调制器产生的是一系列包含各级次衍射图样(并非周期性图样)，而本装置拟在第一衍射级次的位置获得拉盖尔-高斯模式的输出(下见1.2.2节及(4)式)，故需对输出的光束进行相干滤波。试验中引入了4f系统。在4f系统出射透镜的傅里叶焦平面上观测到各级衍射条纹后，通过孔径光阑相干滤波。选择出第一极大条纹。即可得到特定模式的拉盖尔-高斯光束衍射光。这个4f系统和孔径光阑起到了小波滤波变换的作用。
-
基于空间光调制器产生拉盖尔-高斯光束的实验装置示意图如图 1所示。激光二极管发出的基膜激光首先经过凹透镜M1和凸透镜M2扩束，而后入射到起偏器M3上。经过M3的偏振光入射到空间光调制器S1上进行振幅和相位的调制，入射到检偏器M4上。经过检偏器M4的光经过M5和M6构成的4f系统做傅里叶变换及反变换，最终可以在CCD上观测到一系列拉盖尔-高斯模式的衍射图样。通过孔径光阑滤波后，得到拉盖尔-高斯模式输出。
Figure 1. Schematic diagram of generating experimental device of Laguerre-Gaussian beam
实验装置中，M1的焦距为50mm，M2的焦距为200mm, 4f系统M3和M4的焦距为350mm。由于经过4f系统傅里叶变换的光束需要在其焦平面上观测衍射图样，故CCD需配有透镜M7，实验中其焦距为200mm。
当经过M5透镜做傅里叶变换后的光束为不同的拉盖尔-高斯模式时，模场光斑的大小可能会不同，故孔径光阑最好采用可变孔径式，针对不同的入射模式相应调整滤波的位置和大小，以获得更好的光束输出。
-
灰度调制法和二进制全息图法是产生拉盖尔-高斯光束的常见方法。灰度调制法是产生拉盖尔-高斯光束的传统方法，但是其产生的光束是随时间发生相关变化的[8-10]。与此相比，二进制全息图法可以用来产生空间分布更稳定的模式。下面即作者生成用来调制空间光的全息图。
首先，假设输出的光场信号，即拉盖尔-高斯模式为：
$ s(x, y) = A(x, y)\exp [{\rm{i}}\varphi (x, y)] $
(2) 式中，A(x, y)表示光场振幅，φ(x, y)表示光场相位，在[-π, π]内取值。
从数学上说，一个周期性的光栅可以被写为傅里叶级数形式[11-12]：
$ \begin{array}{l} f(x, y) = \sum\limits_n {\{ [\sin (\pi nq)/(\pi n)]} \times\\ \;\;\;\;\exp \{ {\rm{i}}n[2\pi ({u_0}x + {v_0}y) + 2\pi \delta ]\} \} \end{array} $
(3) 式中, (u0, v0)是周期性光栅的空间频率，对应图 1中M5焦平面的位置; q是一个与光栅形状有关的量，即透光部分与不透光部分的宽度比值; δ∈[-1/2, 1/2]是一个与光栅相对位置有关的参量。根据(3)式，第一级次的衍射光场可以表示为[13]：
$ {f_1}(x, y) = [\sin (\pi q)/\pi ]\exp ({\rm{i}}2\pi \delta ) $
(4) 这里，忽略了光场入射到光栅上时可能存在的相位扰动。由于q和δ变化的比光栅的周期慢得多，二者对于光栅位置不具有敏感性，写为位置无关的函数也能得到相对准确的结果。这里假设在第一衍射极大的位置得到目标光场，即f1(x, y)=s(x, y), 由(4)式可将复光场信号的振幅和相位表示为[11-12]：
$ q(x, y) = \arcsin [A(x, y)]/\pi $
(5) $ \delta (x, y) = \varphi (x, y)/(2\pi ) $
(6) 这样就编码表示了拉盖尔-高斯光束光束的振幅和相位信息。理论上讲，对于其它级次衍射光，也可以作类似的处理来使其输出拉盖尔-高斯模式，但是其衍射效率相对较低。
接下来，通过Lee方法生成一幅二进制全息图，其中空间光调制器的透过率可以表示为[13-14]：
$ \begin{array}{l} t(x, y) = 1/2 + {\mathop{\rm sgn}} \{ \cos [2\pi ({u_0}x + {v_0}y) - \\ \;\;\;\;\;\;2\pi \delta (x, y)] - \cos [\pi q(x, y)]\} /2 \end{array} $
(7) 式中，sgn(x)表示符号函数。(7)式实际上就是入射光与出射光之间的传递函数。通过这个传递函数，可以将空间光调制器调制成一个等效光栅，使输入高斯光束时，输出为拉盖尔-高斯光束的傅里叶变换。理论上讲，拉盖尔-高斯、厄米-高斯、贝塞尔-高斯模式的全息图都可以通过(7)式生成，将q和δ因子引入相应模式的表达式中，即可将模拟图转换为二进制全息图。
基于上述原理，可以绘制出经过修正的拉盖尔-高斯二进制全息图，如图 2所示。
Figure 2. The modified Laguerre-Gaussian binary hologram
-
如图 3所示，为l=5，p=0(由于实验中要观测空心光束，故而将p设置为0)时, 得出的经过可变光阑滤波前拉盖尔-高斯光束的衍射图样。通过调整起偏器和检偏器使得中心亮斑使主极大亮度最暗时，可以观测到左上右下的第1级衍射光具有p=0的拉盖尔-高斯光束的空心特征。这就是拉盖尔-高斯模式输出。
Figure 3. Laguerre-Gaussian diffraction pattern before aperture filter
当l取不同数值时，得到的拉盖尔-高斯光束输出图如图 4所示。
Figure 4. Laguerre-Gaussian mode output of different order after aperture filter
实验中观测到:当l=1时，圆环的内环很小; 而随着l逐渐增大至10时，圆环的内环逐渐增大，整个光束的半径也随着增大，这与理论模拟相符。
进一步测量不同l值时，输出光束横向光场分布图案中暗核的直径，将其与拉盖尔-高斯光束理论暗核值径相比较，如图 5所示。图中，横坐标拓扑荷数为无量纲的量，纵坐标单位为cm。
Figure 5. Theoretical and experimental values of diameter of inner ring of Laguerre-Gaussian mode
实验中还观测到，输出光束内核尺寸与理论值在误差允许范围内符合较好。随着l的增加，暗核半径线性增加，这与拉盖尔-高斯光束的性质一致[15]。此外，输出光束在传播过程中是发散的，这表明输出的光束为拉盖尔-高斯光束。
实验中还观测到，当l分别为1，2，3时，输出的LG光束圆度较好，光束也比较均匀，而当输出光束阶数逐渐增加时，输出的光束会体现出一定的不均匀性，这一方面是由于空间光调制器的晶格与输入调制光场的匹配程度问题，另一方面是由于实验条件所限，输入CCD之前调制的光场可能存在一定的不均匀性。这也是造成实验值与理论值之间差异的原因(见图 5)。
-
在图 4的拉盖尔-高斯光束输出图样中，观测到了环形的光场分布，但这只能证明光场振幅具有空心的光场分布，并不能证明其具有螺旋的相位波前。
于是进一步将前面所述的空心拉盖尔-高斯光束(即p=0，l取不同值的光束)通过双缝衍射，可以通过CCD观测输出的图样, 如图 6所示。
Figure 6. Diffraction pattern formed by beam through double slit when l=2, p=0
如图 6所示，观测到了斜条纹状衍射结果，这初步证明了实验产生光束不仅具有空心的光场分布，也具有螺旋的相位波前[16]，即产生了涡旋光束输出。
进一步地通过优化光路(如对每个透镜加入2维调节架以精确控制其俯仰)、提高输入激光器的光束质量等，可以提高输出光束的光束质量。这样最终通过双缝的斜纹波条纹将更利于观测，也可以进一步用于精确研究光束的轨道角动量等特性，这也是该项目进一步的研究方向。
-
从理论和实验上提出了一种基于空间光调制器产生拉盖尔-高斯光束以及产生涡旋光束的方法。通过二进制全息图法生成了可用于空间光调制器的全息图；搭建了实验平台实际产生了拉盖尔-高斯模式；对输出的拉盖尔-高斯模式做了检验。
实验中输出了l=10及l=20的拉盖尔-高斯模式。在传统基于谐振腔的拉盖尔-高斯模式产生方法中，通常由于损耗是无法产生阶数如此高的模式的。从这个角度讲，基于空间光调制器的拉盖尔-高斯光束产生方法由于基于计算机模拟调制，其损耗相对于传统方法较小，故具有产生高阶拉盖尔-高斯光束的便捷性。
在研究时假设模式系数p=0以得到空心的光束输出，若想要得到不同模式系数的LG光束, 也可以在生成全息图时假设相应的模式系数，以得到相应的光束输出。
空间光调制器产生拉盖尔-高斯光束方法研究
Generation of Laguerre-Gaussian beam based on spatial light modulator
-
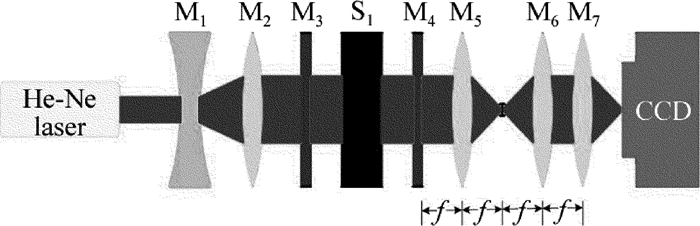
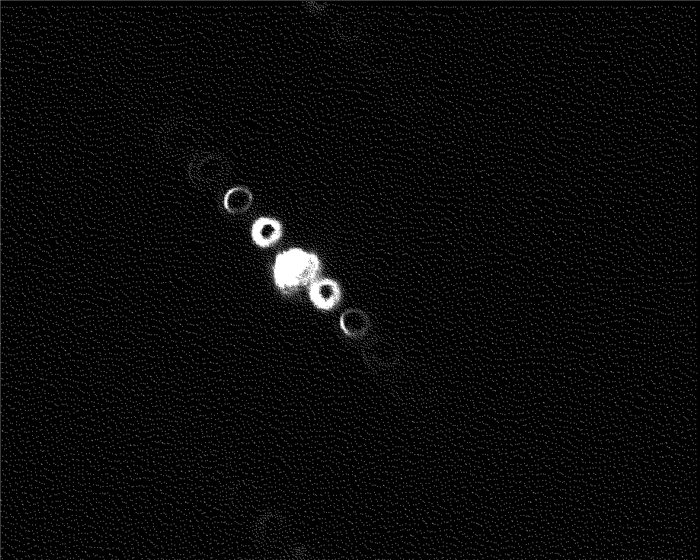
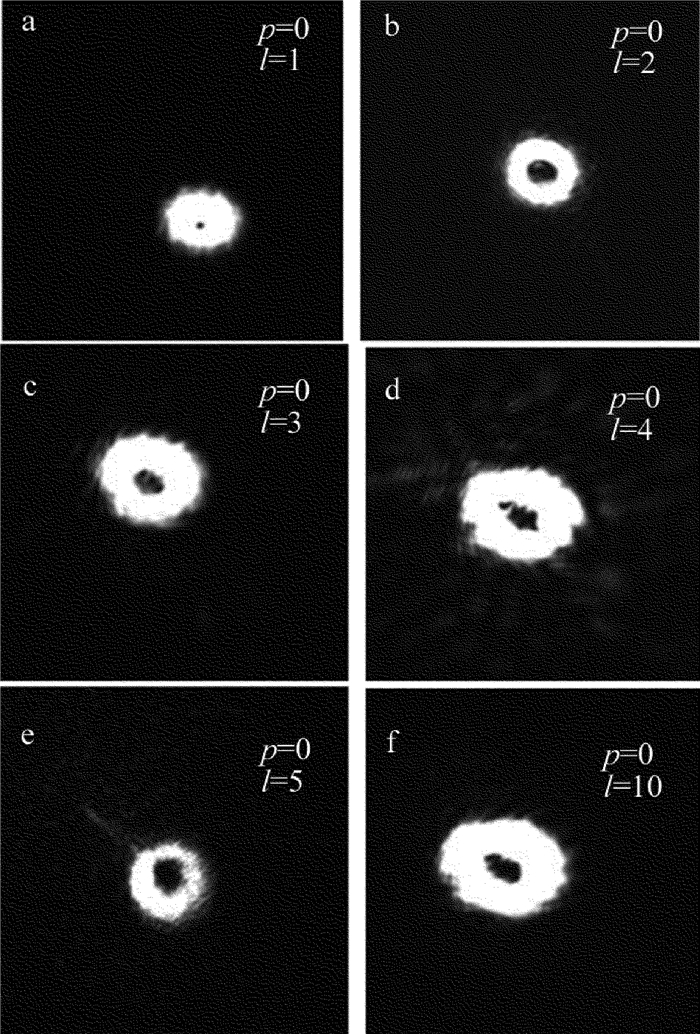
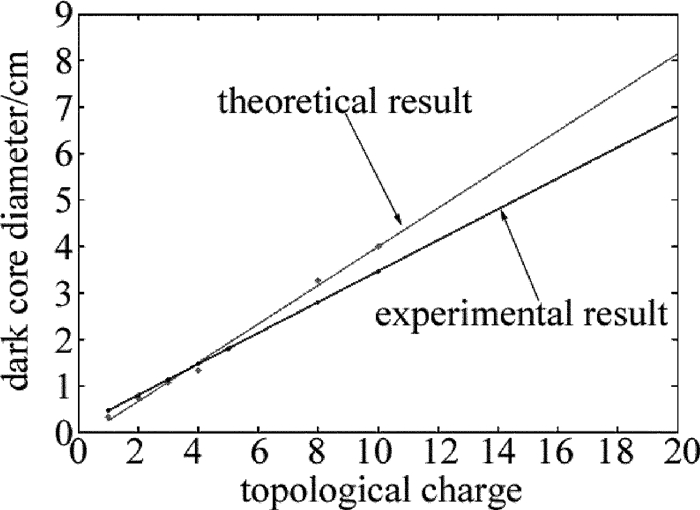
摘要: 为了解决产生拉盖尔-高斯模式光束较难的问题，采用二进制振幅全息图方法，基于空间光调制器，产生了拉盖尔-高斯光束，进行了理论分析和实验验证。推导了高斯光束到拉盖尔-高斯光束傅里叶变换的传递函数，通过对拉盖尔-高斯模拟图的修正，得出了可以用于空间光调制器的二进制全息图; 搭建了基于4f系统的实验平台，取得了不同阶数的拉盖尔-高斯模式输出，并在实验中对产生的拉盖尔-高斯光束进行了检测。结果表明，此套装置搭建及操作简便，且可实现动态可控的光束输出，对于产生高阶涡旋光束以及因斯-高斯模式都有重要意义。Abstract: In order to handle the difficulty in generating Laguerre-Gaussian mode, the binary amplitude hologram method based on spatial light modulator was presented to produce Laguerre-Gaussian beam. After theoretical analysis and experimental verification, the transfer function of Fourier transform from Gaussian beam to Laguerre-Gaussian beam was derived. Binary hologram which can be used in spatial light modulator was obtained after modifing Laguerre-Gaussian mode simulation. Experimental platform based on 4f system was setup and Laguerre-Gaussian modes of different orders were observed and tested. The results show that, it is easy to build and operate the device conveniently and the device can realize beam output dynamically and controllably. The study is important for the generation of high-order vortex beams and Ince-Gaussian model.
-
Figure 1. Schematic diagram of generating experimental device of Laguerre-Gaussian beam
Figure 5. Theoretical and experimental values of diameter of inner ring of Laguerre-Gaussian mode
-
[1] LI Sh M, WANG Y, HU A J, et al. A method of forming annular light[J].Laser Technology, 2015, 39(5):621-624(in Chinese). [2] SWARTZLANDER G A. Peering into darkness with a vortex spatial filter[J]. Optics Letters, 2001, 26(8): 497-499. doi: 10.1364/OL.26.000497 [3] WEI Y, ZHU Y Y. Analysis of phase change of Laguerre-Gaussian vortex beam during propagation[J].Laser Technology, 2015, 39(5):723-726(in Chinese). [4] ZHEN Zh, LIU Y X, LV B D. Propagation properties of Hermite-Lauguerre Guassian beams[J].Laser Technology, 2005, 29(6):641-644(in Chinese). [5] YAO A M, PADGETT M J. Orbital angular momentum: origins, behavior and applications[J]. Advances in Optics and Photonics, 2011, 3(2): 161-204. doi: 10.1364/AOP.3.000161 [6] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review, 1992, A45(11): 8185. [7] REN Y X, LI M, HUANG K, et al. Experimental generation of Laguerre-Gaussian beam using digital micromirror device[J]. Applied Optics, 2010, 49(10): 1838-1844. doi: 10.1364/AO.49.001838 [8] LERNER V, SHWA D, DRORI Y, et al. Shaping Laguerre-Gaussian laser modes with binary gratings using a digital micromirror device[J]. Optics Letters, 2012, 37(23): 4826-4828. doi: 10.1364/OL.37.004826 [9] GONG L, REN Y X, XUE G S, et al. Generation of nondiffracting Bessel beam using digital micromirror device[J]. Applied Optics, 2013, 52(19): 4566-4575. doi: 10.1364/AO.52.004566 [10] MIRHOSSEINI M, MAGANA-LOAIZA O S, CHEN C, et al. Rapid generation of light beams carrying orbital angular momentum[J]. Optics Express, 2013, 21(25): 30196-30203. doi: 10.1364/OE.21.030196 [11] RODENBURG B, MIRHOSSEINI M, MAGAN~A-LOAIZA O S, et al. Experimental generation of an optical field with arbitrary spatial coherence properties[J]. Journal of the Optical Society of America, 2013, B31(6): 251-260. [12] CONKEY D B, CARAVACA-AGUIRRE A M, PIESTUN R. High-speed scattering medium characterization with application to focusing light through turbid media[J]. Optics Express, 2012, 20(2): 1733-1740. doi: 10.1364/OE.20.001733 [13] LEE W H. Binary computer-generated holograms[J]. Applied Optics, 1979, 18(21): 3661-3669. doi: 10.1364/AO.18.003661 [14] ARRIZÓN V, MÉNDEZ G, SÁNCHEZ-DE-LA-LLAVE D. Accurate encoding of arbitrary complex fields with amplitude-only liquid crystal spatial light modulators[J]. Optics Express, 2005, 13(20): 7913-7927. doi: 10.1364/OPEX.13.007913 [15] MELLINGHOFF I K, WANG M Y, VIVANCO I, et al. Molecular determinants of the response of glioblastomas to EGFR kinase inhibitors[J]. New England Journal of Medicine, 2005, 353(19): 2012-2024. doi: 10.1056/NEJMoa051918 [16] ZHOU H, YAN S, DONG J, et al. Double metal subwavelength slit arrays interference to measure the orbital angular momentum and the polarization of light[J]. Optics Letters, 2014, 39(11): 3173-3176. doi: 10.1364/OL.39.003173 -
点击查看大图
图(6)
计量
- 文章访问数: 5885
- HTML全文浏览量: 3913
- PDF下载量: 24
- 被引次数: 0
