一种带宽展宽的等离子体超材料吸波体的设计

张浩; 马宇; 章海锋; 杨靖; 刘佳轩

doi:10.7510/jgjs.issn.1001-3806.2019.02.020

一种带宽展宽的等离子体超材料吸波体的设计

张浩¹,
马宇¹,
章海锋^1,2,3, ,,
杨靖¹,
刘佳轩¹

1.
南京邮电大学电子与光学工程、微电子学院, 南京 210023
2.
南京邮电大学电子科学与技术国家级实验教学示范中心, 南京 210023
3.
南京邮电大学信息电子技术国家级虚拟仿真实验教学中心, 南京 210023

基金项目:

国家级大学生创新训练计划资助项目 SZDG2017009

详细信息

作者简介:
张浩(1996-), 男, 大学本科生, 现主要从事超材料吸波器、电磁超材料的研究

通讯作者:
章海锋, E-mail:hanlor@163.com

中图分类号: O436;O53
计量
- 文章访问数: 3
- HTML全文浏览量: 1
- PDF下载量: 5
出版历程
- 收稿日期: 2018-04-16
- 修回日期: 2018-06-28
- 发布日期: 2019-03-24

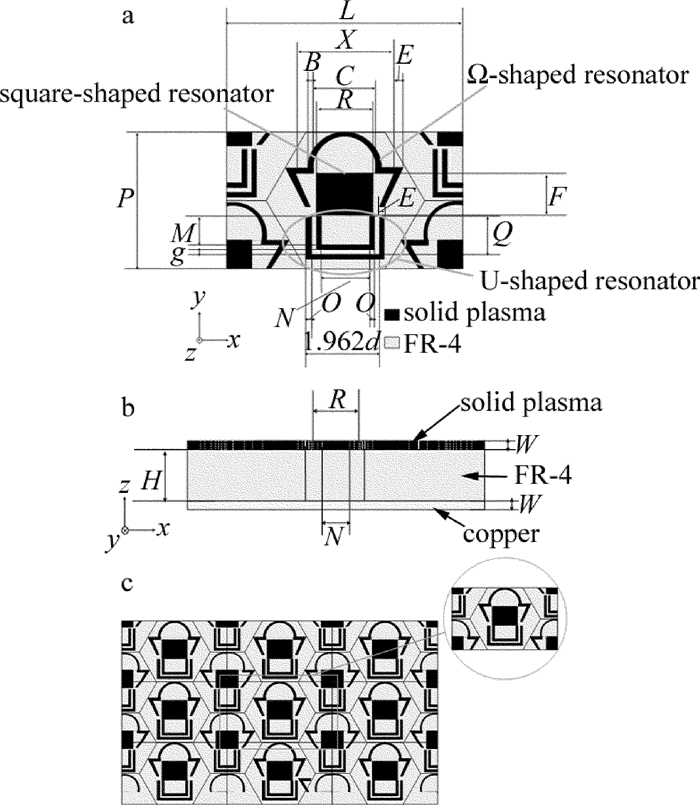
Design of a band enhanced absorber based on plasma metamaterial

1.
College of Electronic and Optical Engineering & College of Microelectronics, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
2.
National Electronic Science and Technology Experimental Teaching Demonstrating Center, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
3.
National Information and Electronic Technology Virtual Simulation Experiment Teaching Center, Nanjing University of Posts and Telecommunications, Nanjing 210023, China

摘要

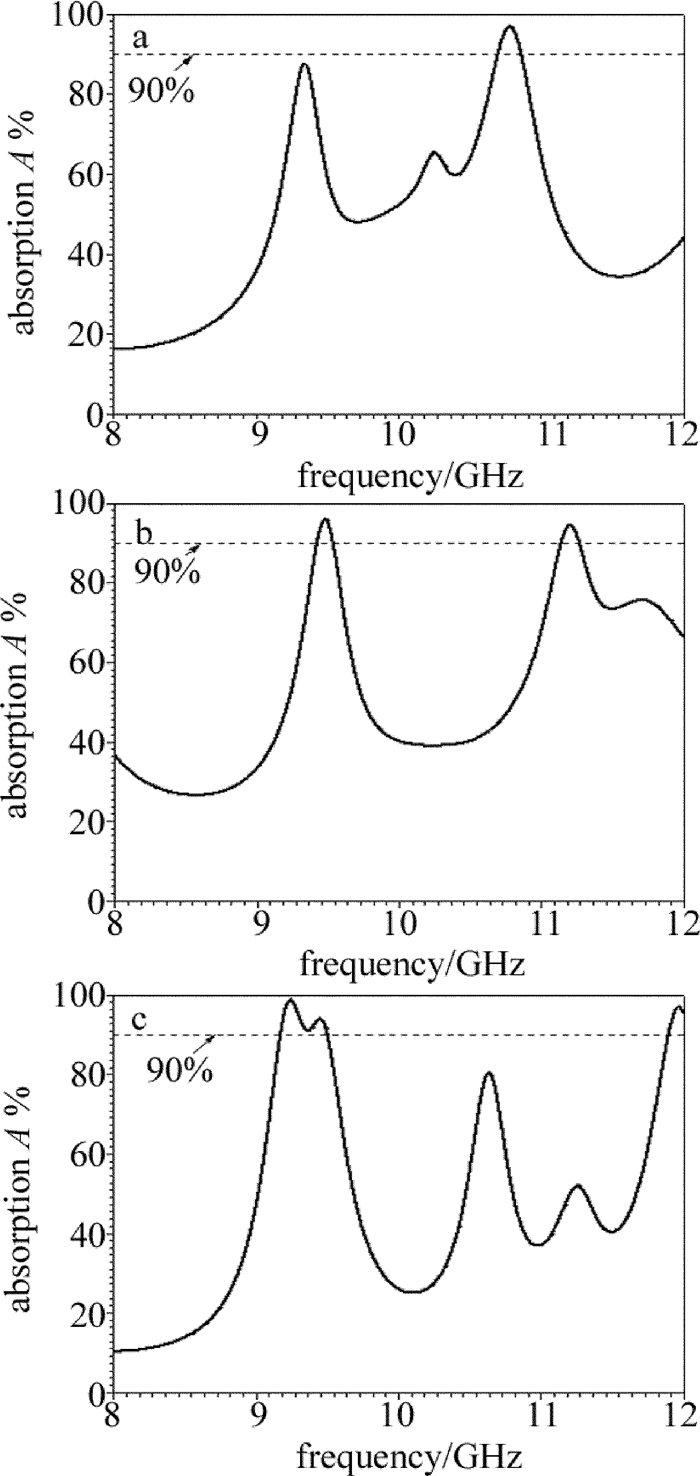
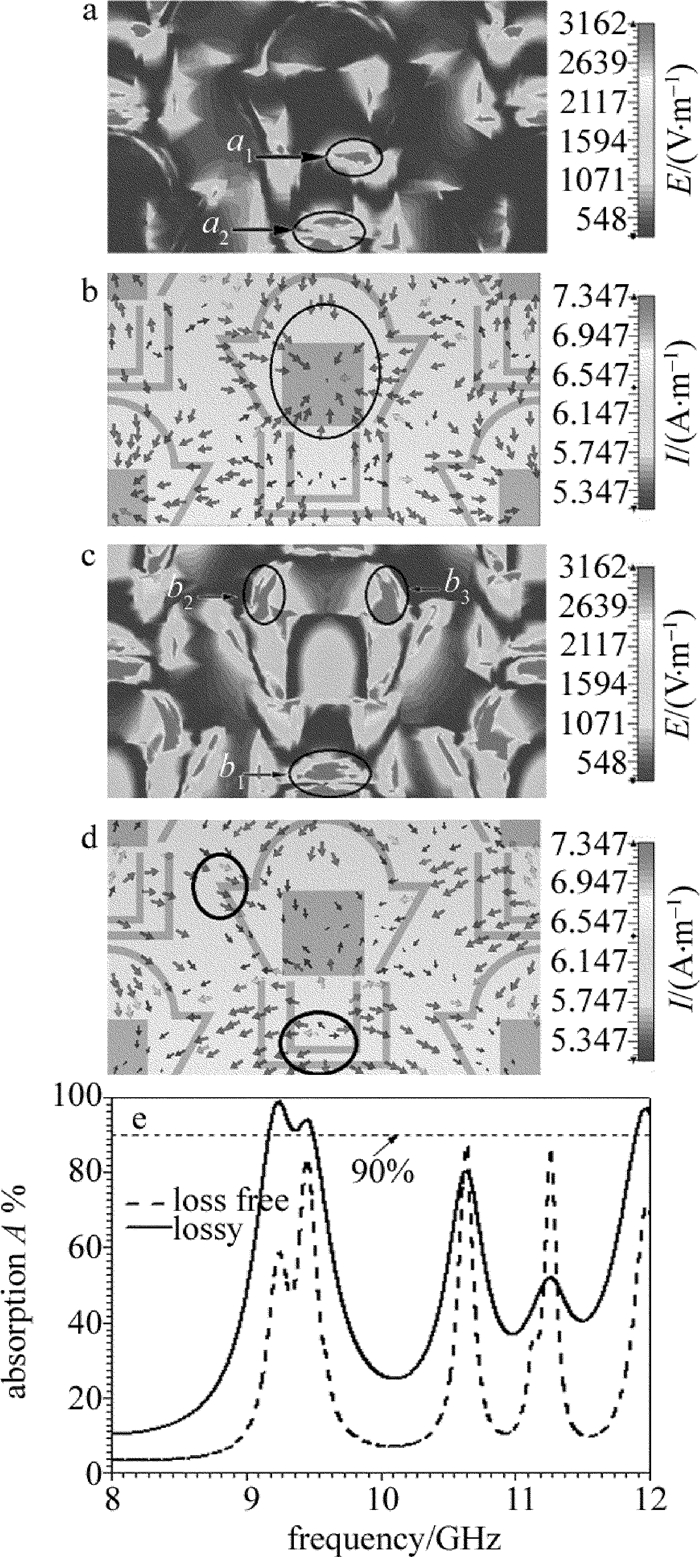
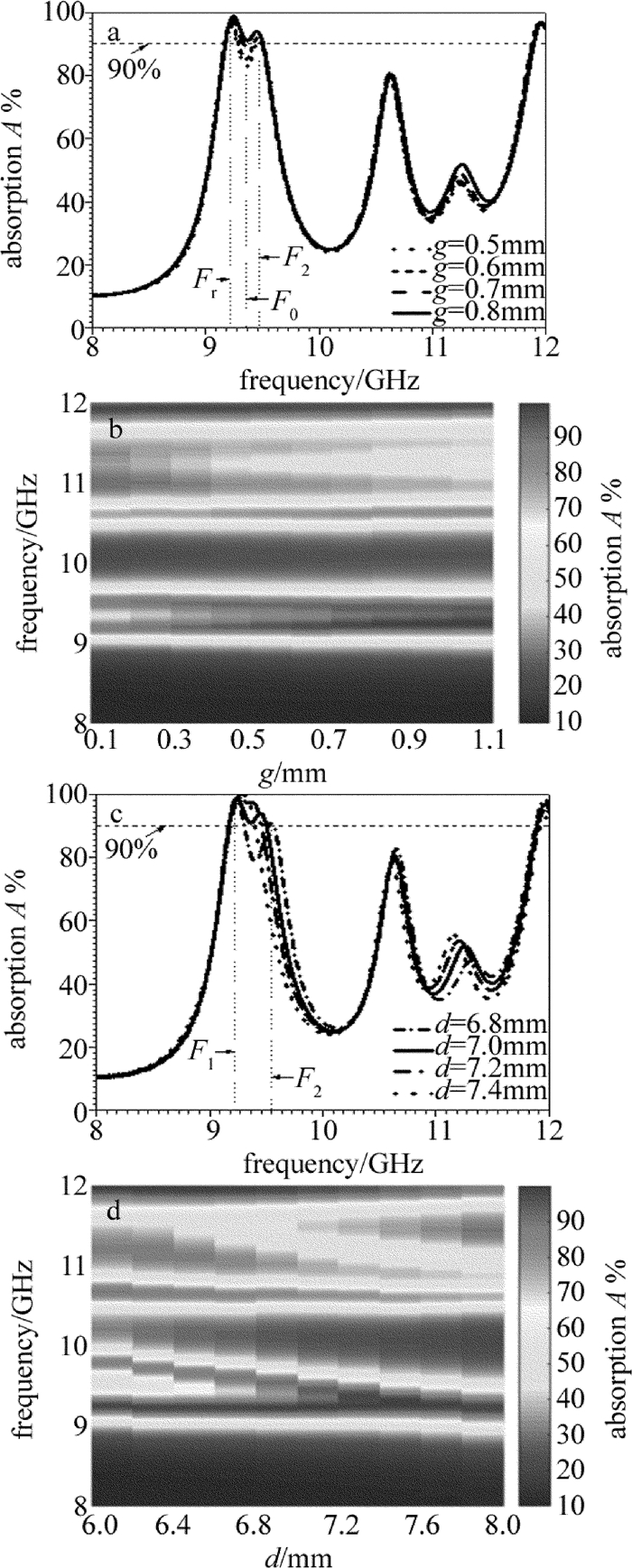
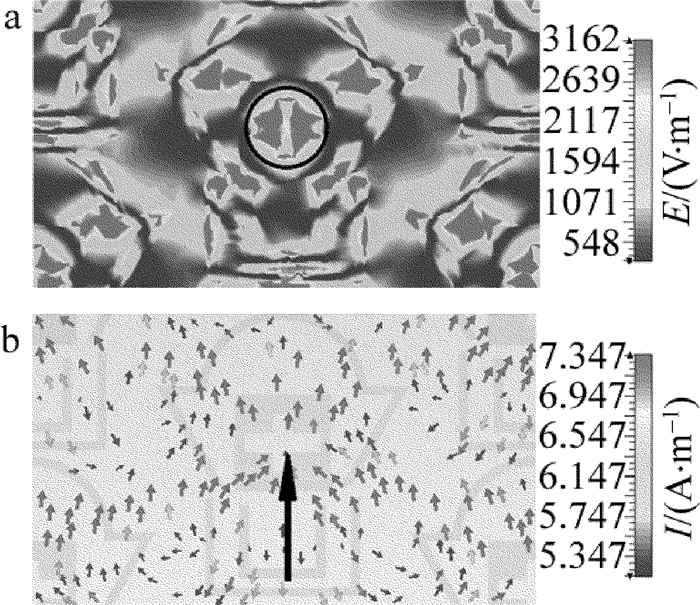
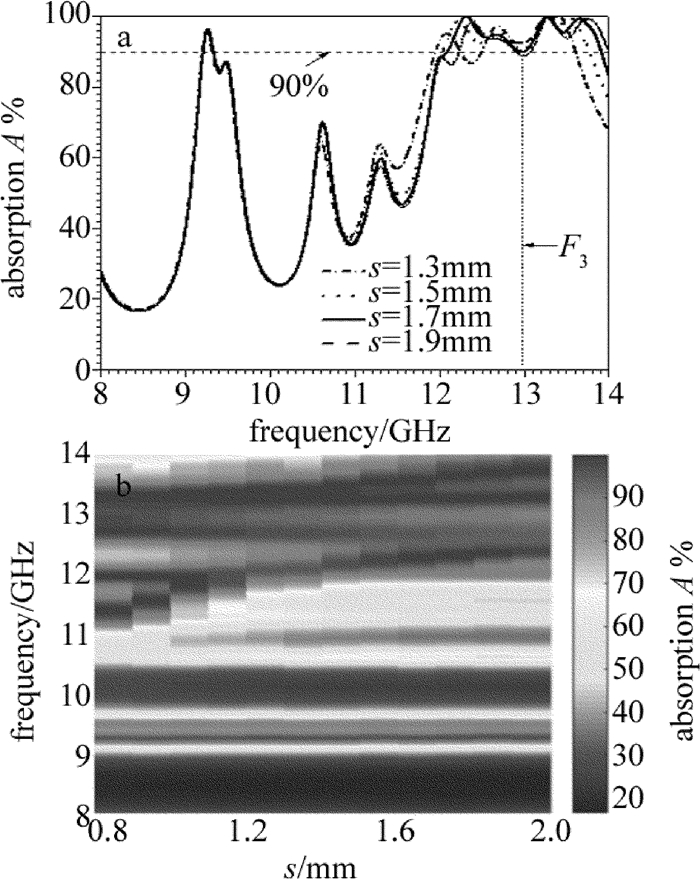
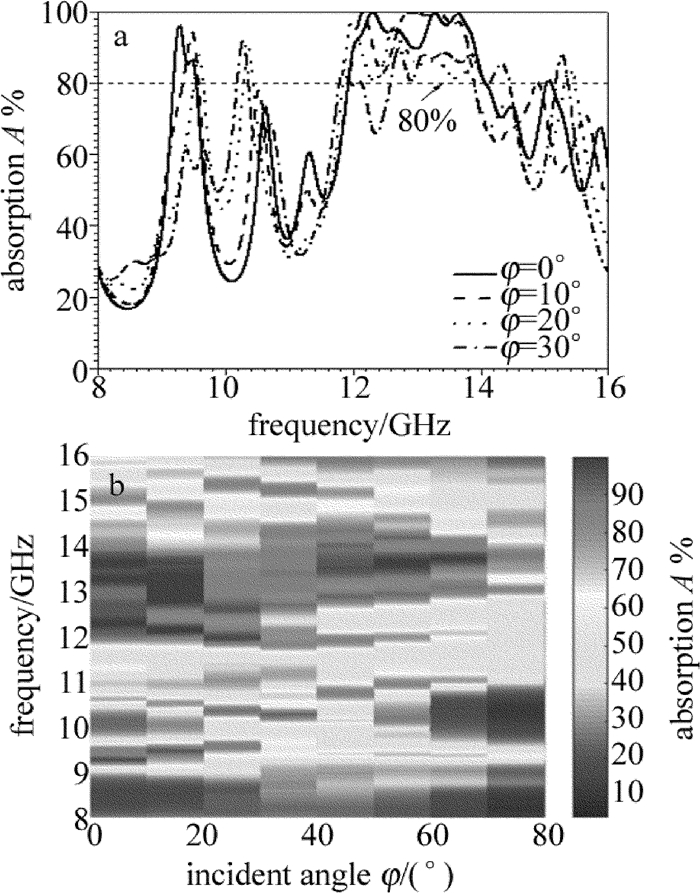
摘要: 为了在TE波下获得带宽可展宽（11GHz~14GHz频带内）且可调谐的吸收曲线，提出了一种新型超材料吸波体，其周期性结构单元采用蜂窝状特有的六边形结构。对该吸波体的参量分析图进行了计算，研究了变量g和d的数值不同时，对吸波体吸收频带及吸收带宽的影响，并解释了蚀刻"十"字形结构吸波体带宽展宽的成因。结果表明，该吸波体在9.17GHz~9.5GHz低频频域的吸收率达到90%以上，当不同的等离子体谐振区域被激励时，可以实现吸波体的分时分频域吸收以及改善吸波体的吸收性能，改变变量g和d可以实现对吸收频带的动态调控；可以通过在方形结构中蚀刻"十"字形结构的方式拓宽高频频域的吸收带宽，其在12.08GHz~13.91GHz频域的吸收率高于90%，改变变量s可以明显展宽吸收频带，且该吸波体对入射电磁波的角度不敏感。该吸波体的设计思路为拓宽吸波体的吸收带宽提供了一种有效的方法。
- 光学器件 /
- 超材料吸波体 /
- 全波仿真法 /
- 带宽展宽
Abstract: In order to achieve the absorption curve with broadening (within 11GHz~14GHz band) and tunable bandwidth under TE wave, a new metamaterial absorber was proposed whose periodic structural unit adopted honeycomb-shaped hexagonal structure.The parametric analysis chart of the absorber was calculated.The effects of variables g and d on absorbing band and absorbing bandwidth were studied.The cause of bandwidth broadening of the etched cross-shaped absorber was also explained.The results show that, absorption rate of the absorber in the low frequency domain at 9.17GHz~9.5GHz is over 90%.When different plasma resonance regions are excited, the time-frequency domain absorption of the absorber can be realized.And the absorptive capacity of the absorber can be improved.By changing the variables g and d, the dynamic control of the absorption band can be realized.The absorption bandwidth in the high frequency domain can be widened by etching cross-shaped structure in a square structure.Its absorption rate in the frequency domain of 12.08GHz~13.91GHz is higher than 90%.By changing the variable s, the absorption band can be obviously widened.The absorber is insensitive to the angle of incident electromagnetic wave.The design idea provides an effective way to broaden the absorption bandwidth of absorbers.
- optical devices /
- metamaterial absorber /
- full-wave simulation /
- band enhancement

HTML全文

引言

自动化生产线上的工件姿态测量及抓取是重要工艺环节。在姿态变换实验平台的研究方面，HUANG^[1]等人采用欧拉角物体姿态对机器人的空间运动进行描述。JIANG等人^[2]研究了海豚尾鳍俯仰-沉浮运动的数学模型，并建立了描述豚尾各运动参量之间关系的运动学方程。CHEN等人^[3]提出了圆结构光视觉姿态测量模型，基于单目视觉和激光圆结构光实现了目标姿态测量。YU等人^[4]采用中轴线法对火箭空间轴对称目标的俯仰角和偏航角进行测量，并进行了误差分析；利用目标图像信息提高测量精度，采用间接方法提取目标中轴线，避免了多相机目标匹配问题。LI等人^[5]对相机系统进行了标定，并用单相机对六自由度(six-degree of freedom，6-DOF)机构的6个自由度进行了基于图像的位移测量；将6个自由度位移的仿真结果作为理想数据与实测数据进行比较获得测量误差。

国外学者在20世纪80年代前后，提出了姿态测量中的透视n点定位问题(perspective-n-point, PNP)。该方法为基于单帧图像的姿态解算方法：已知被测目标物体上n个特征点中任意两个点间的对应坐标关系，根据摄像机的成像模型可以确定目标物体上这n个特征点在摄像机坐标系中的坐标，再利用标定后的摄像机内外参量求出特征点在世界坐标系中的坐标值，最终解算出目标物体的姿态参量。1981年, FISCHLER和BOLLES建立了数学模型，提出了一种封闭式解法，为视觉姿态测量提供了理论基础^[6]。2009年, LEPETIT等人提出了一种对N≥4的PNP问题均适用的解算方法，将所有特征点表示为4个虚拟控制点的PNP问题非迭代算法，将PNP问题简单地转换为估计解算4个虚拟控制点在摄像机坐标系的坐标值问题^[7]。STEWÉNIUS等人^[8]提出了5点相对姿态的定位算法，且该方法多数情况下优于直接法。

为实现工件的姿态变换，并测量不同变换条件下对应的工件姿态参量，设计了6-DOF姿态变换实验平台，实验平台具有两种基本的实验功能：工件的各种姿态变换，由变换平台3个平移自由度及3个旋转自由度组合实现；视觉测量系统，由单目相机配合激光结构光实现。

构建的实验平台由x方向平移台、y方向平移台及z方向升降台组成位置调节部件；由γ方向水平旋转台、β方向俯仰转角台及α方向侧倾转角台构成姿势调节部件，通过滑动副及旋转副的组合运动，实现工件的不同姿态变换。在分析Denavit-Hartenberg(D-H)模型原理基础上，构建了姿态变换实验平台的运动学数学模型，求得了D-H模型参量及姿态传递变换矩阵；同时，依据小孔成像机理，构建了视觉系统内外参量模型，为基于实验平台的工件姿态视觉测量提供了条件^[9-10]。通过对环形激光结构光图像的分割，获得环形光条，并用光条图像的法向量结合坐标系间的转换，得到工件表面在世界坐标系中的法向量，进而反演实现工件姿态的计算。

1. 六自由度姿态变换实验平台原理

六自由度姿态模拟平台如图 1所示。实验平台由x方向平移台、y方向平移台、z方向升降台组成位置调节系统；由γ方向360°旋转台、β方向转角台、α方向转角台构成姿势调节系统。

Figure 1. Functional component of 6-DOF attitude simulation experiment platform system

下载: 全尺寸图片幻灯片

由3个直线运动、3个旋转运动的组合，具备位置及姿态调整功能，末端工作平面可模拟空间限定范围内的任意位置、任意姿态。姿态变换平台与视觉系统相结合，可实现不同姿态下的工件视觉识别及视觉测量等功能。

图 2为姿态变换平台6个自由度的功能部件组合及其坐标系示意图。主要技术参量为：绕x轴的旋转角度α=±15°，分辨率0.1°；绕y轴旋转的角度β=±15°，分辨率0.1°；绕z轴旋转的角度γ=360°，分辨率0.1°。沿x轴方向的直线运动范围为75mm，分辨率0.01mm；沿y轴方向的直线运动范围为75mm，分辨率0.02mm；沿z轴方向的直线运动范围为13mm，分辨率0.01mm。

Figure 2. 6-DOF attitude simulation experiment platform and its coordinate system

下载: 全尺寸图片幻灯片

2. 六自由度姿态变换实验平台模型

D-H方法适用于任何由关节和连杆组成的机器人模型构建，而机器人本质上大多由一组关节和连杆构成。当所有关节变量为已知时，可用正运动学模型确定机器人末端位姿；相反，若对末端位置及姿态有特定要求，则可用逆运动学实现对每一关节变量的逆向求解。

2.1 机器人关节变换的D-H建模原理

六自由度模拟平台可以抽象为连杆-关节机器人结构，从而应用D-H方法进行模型构建。正常情况下，机器人的每个关节有一个自由度，可为滑动的或转动的。图 3为典型的用D-H法表示的机器人连杆-关节模型结构。图中连续的3个关节由两个连杆连接, 关节分别为J_n, J_n+1及J_n+2，连杆分别为n及n+1。3个旋转关节的z轴与关节旋转方向之间遵循右手螺旋法则，旋转角θ为关节变量；若为滑动关节，则沿z轴的连杆滑动长度定义为关节变量^[11-12]。关节的x轴一般定义在两个相邻关节轴线的公垂线上。图中，关节J_n与J_n+1之间的关节偏移量为a_n，关节J_n+1与J_n+2之间的关节偏移量为a_n+2；两相邻的公垂线之间的距离为d，两相邻的关节的z轴之间夹角定义为关节扭转角，分别为α_n和α_n+1。

Figure 3. Typical D-H bar-joint model for robot

下载: 全尺寸图片幻灯片

为实现关节之间的变换，在每一个关节上建立一个参考坐标系。从关节J_n+1到关节J_n+2的变换过程为^[13-14]：(1)关节J_n+2绕关节J_n+1旋转θ_n+1角度，有旋转算子rot(z_n, θ_n+1)，使得x_n轴与x_n+1轴平行, 此时x_n轴与x_n+1轴在同一平面上，将x_n+1轴平移d_n+1，有平移算子trans(0, 0, d_n+1)，即可使二者重叠; (2)将关节J_n+1沿x_n轴平移a_n+1，记为trans(a_n+1, 0, 0)，使得x_n轴与x_n+1轴的坐标原点重合; (3)通过旋转α_n+1角度，将z_n轴绕x_n+1轴转到与z_n+1轴重叠，记为rot(x, a_n+1), 此时，关节J_n+1的坐标系与关节J_n+2的坐标系重合，实现了坐标系之间的转换。

从关节J_n+1到关节J_n+2的变换矩阵记作ⁿT_{n + 1}，对应的矩阵A_n+1由上述变换过程各自对应的矩阵右乘得到，有：

$\begin{array}{*{20}{c}} {{}^n{\mathit{\boldsymbol{T}}_{n + 1}} = }\\ {{\mathit{\boldsymbol{A}}_{n + 1}} = {\rm{rot}}\left( {{z_n},{\theta _{n + 1}}} \right) \times {\rm{trans}}\left( {0,0,{d_{n + 1}}} \right) \times }\\ {{\rm{trans}}\left( {{a_{n + 1}},0,0} \right) \times {\rm{rot}}\left( {x,{a_{n + 1}}} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos {\theta _{n + 1}}}&{ - \sin {\theta _{n + 1}}}&0&0\\ {\sin {\theta _{n + 1}}}&{\cos {\theta _{n + 1}}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&{{d_{n + 1}}}\\ 0&0&0&1 \end{array}} \right] \times }\\ {\left[ {\begin{array}{*{20}{c}} 1&0&0&{{a_{n + 1}}}\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{\cos {\alpha _{n + 1}}}&{ - \sin {\alpha _{n + 1}}}&0\\ 0&{\sin {\alpha _{n + 1}}}&{\cos {\alpha _{n + 1}}}&0\\ 0&0&0&1 \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos {\theta _{n + 1}}}&{ - \sin {\theta _{n + 1}}\cos {\alpha _{n + 1}}}&{\sin {\theta _{n + 1}}\sin {\alpha _{n + 1}}}&{{a_{n + 1}}\cos {\theta _{n + 1}}}\\ {\sin {\theta _{n + 1}}}&{\cos {\theta _{n + 1}}\cos {\alpha _{n + 1}}}&{ - \cos {\theta _{n + 1}}\sin {\alpha _{n + 1}}}&{{a_{n + 1}}\sin {\theta _{n + 1}}}\\ 0&{\sin {\alpha _{n + 1}}}&{\cos {\alpha _{n + 1}}}&{{d_{n + 1}}}\\ 0&0&0&1 \end{array}} \right]} \end{array}$

(1)

对于具有6个关节的机器人，从机器人的基座R开始，到机器人手爪末端的变换过程可表示为：

${}^{\rm{R}}{\mathit{\boldsymbol{T}}_6} = {}^{\rm{R}}{\mathit{\boldsymbol{T}}_1}{}^{\rm{1}}{\mathit{\boldsymbol{T}}_2}{}^{\rm{2}}{\mathit{\boldsymbol{T}}_3}{}^{\rm{3}}{\mathit{\boldsymbol{T}}_4}{}^{\rm{4}}{\mathit{\boldsymbol{T}}_5}{}^{\rm{5}}{\mathit{\boldsymbol{T}}_6} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{A}}_4}{\mathit{\boldsymbol{A}}_5}{\mathit{\boldsymbol{A}}_6}$

(2)

可知，具有6个自由度的机器人，每个自由度对应一个A矩阵。

2.2 六自由度模拟平台D-H运动学模型

六自由度姿态变换平台坐标系如图 4所示。坐标系由3个滑动副、3个转动副组成。每两个运动副公垂线之间的距离分别为d₁, d₂, d₃, d₄, d₅, d₆。按右手螺旋法则，确定关节变量旋转角θ₁~θ₆及两相邻关节的z轴之间关节扭转角α₀~α₅。

Figure 4. D-H coordinate system of attitude simulation experiment platform

下载: 全尺寸图片幻灯片

由坐标系，得到姿态变换平台从平台的基座到末端之间变换的D-H参量表，如表 1所示。

Table 1. D-H parameter table of attitude simulation experiment platform

connecting rod i	angle θ_i/(°)	spacing d_i	connecting rod length a_i-1/mm	twist angle α_i-1/(°)
1	-90	0	0	-90
2	-90	d₂	0	-90
3	0	d₃	0	-90
4	0	d₄	0	0
5	90	d₅	0	90
6	0	d₆	0	90

下载: 导出CSV

| 显示表格

由D-H参量表，求得各个关节的变换矩阵分别为：

$\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&0&{ - \sin {\theta _1}}&0\\ {\sin {\theta _1}}&0&{\cos {\theta _1}}&0\\ 0&{ - 1}&0&0\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&1&0\\ { - 1}&0&0&0\\ 0&{ - 1}&0&0\\ 0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _2}}&{ - \sin {\theta _2}}&0&{{a_2}\cos {\theta _2}}\\ {\sin {\theta _2}}&{\cos {\theta _2}}&0&{{a_2}\sin {\theta _2}}\\ 0&0&1&{{d_2}}\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ { - 1}&0&0&0\\ 0&0&1&{{d_2}}\\ 0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_3} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _3}}&{ - \sin {\theta _3}}&0&{{a_3}\cos {\theta _3}}\\ {\sin {\theta _3}}&{\cos {\theta _3}}&0&{{a_3}\sin {\theta _3}}\\ 0&0&1&{{d_3}}\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&{{d_3}}\\ 0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_4} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _4}}&0&{\sin {\theta _4}}&0\\ {\sin {\theta _4}}&0&{ - \cos {\theta _4}}&0\\ 0&1&0&0\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&0&{ - 1}&0\\ 0&1&0&0\\ 0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_5} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _5}}&0&{ - \sin {\theta _5}}&0\\ {\sin {\theta _5}}&0&{\cos {\theta _5}}&0\\ 0&{ - 1}&0&0\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&{ - 1}&0\\ 1&0&0&0\\ 0&{ - 1}&0&0\\ 0&0&0&1 \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_6} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _6}}&{ - \sin {\theta _6}}&0&0\\ {\sin {\theta _6}}&{\cos {\theta _6}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]} \end{array}$

(3)

由(3)式可得基座R到末端H总的变换矩阵为：

${}^{\rm{R}}{\mathit{\boldsymbol{T}}_{\rm{H}}} = {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{A}}_3}{\mathit{\boldsymbol{A}}_4}{\mathit{\boldsymbol{A}}_5}{\mathit{\boldsymbol{A}}_6} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{{d_2} + {d_3}}\\ 0&{ - 1}&0&0\\ 0&0&{ - 1}&0\\ 0&0&0&1 \end{array}} \right]$

(4)

3. 六自由度姿态变换平台视觉系统模型

3.1 小孔成像模型

姿态变换平台的视觉系统采样单目相机结合激光结构光结构，可实现对平台上的工件进行姿态识别及尺寸测量。相机的单目小孔成像模型如图 5所示。图中，x_wy_wz_w为世界坐标系，相机光轴中心点O与x_c, y_c, z_c轴构成相机直角坐标系，相机等效成像平面Γ的坐标原点O₀是以像素为单位的图像坐标系的原点，(u, v)为图像像素坐标系中任一点的坐标，O₁是以mm为单位的图像坐标系原点，其像素坐标记为(u₀, v₀)。OO₁即为相机焦距f。设景物点p₁在相机坐标系下的坐标为(x_c，y_c，z_c)，p₁点在成像平面上的成像点p₂的坐标为(X，Y，Z)^[15-16]。

Figure 5. Pinhole imaging coordinate system of experimental platform

下载: 全尺寸图片幻灯片

采用齐次坐标与矩阵形式，成像平面上的任一点在u-O₀-v及X-O₁-Y坐标系间的坐标关系可表示为：

$\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\rm{d}}X}}}&0&{{u_0}}\\ 0&{\frac{1}{{{\rm{d}}Y}}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 1 \end{array}} \right]$

(5)

景物点p₁与其成像点p₂间的坐标关系为：

$\left\{ \begin{array}{l} {x_{\rm{c}}}/{z_{\rm{c}}} = X/Z = X/f\\ {y_{\rm{c}}}/{z_{\rm{c}}} = Y/Z = Y/f \end{array} \right.$

(6)

由(5)式将成像平面上的成像点(X，Y)转换为图像点(u, v)，再代入(6)式，得到相机内参量模型：

$\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_X}}&0&{{u_0}}\\ 0&{{k_Y}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{c}}}/{z_{\rm{c}}}}\\ {{y_{\rm{c}}}/{z_{\rm{c}}}}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{M}}_{{\rm{in}}}}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{c}}}/{z_{\rm{c}}}}\\ {{y_{\rm{c}}}/{z_{\rm{c}}}}\\ 1 \end{array}} \right]$

(7)

式中， ${k_X} = \frac{f}{{{\rm{d}}X}}$ 是X轴方向的放大系数； ${k_Y} = \frac{f}{{{\rm{d}}Y}}$ 是Y轴方向的放大系数；M_in是相机内参量矩阵，描述工件表面点与图像点间的关系。外参量模型描述工件表面点坐标与相机坐标间的关系，坐标系x_w-O_w-y_w-z_w在坐标系x_c-O-y_c-z_c中的关系表达式构成相机外参量模型：

$\left[ {\begin{array}{*{20}{c}} {{x_{\rm{c}}}}\\ {{y_{\rm{c}}}}\\ {{z_{\rm{c}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}}\\ {{y_{\rm{w}}}}\\ {{z_{\rm{w}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{p}}\\ {{\mathit{\boldsymbol{o}}^{\rm{T}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}}\\ {{y_{\rm{w}}}}\\ {{z_{\rm{w}}}}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{M}}_{\rm{w}}}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}}\\ {{y_{\rm{w}}}}\\ {{z_{\rm{w}}}}\\ 1 \end{array}} \right]$

(8)

式中，(x_w，y_w，z_w)为景物点在世界坐标系中的坐标；M_w是摄像机外参量矩阵；n =[n_x n_y n_z]^T为x_w轴在相机坐标系x_c-O-y_c-z_c中的方向向量；o =[o_x o_y o_z]^T为y_w轴在相机坐标系x_c-O-y_c-z_c中的方向向量； $\mathit{\boldsymbol{R}} = \left[{\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}\\ {{n_z}}&{{o_z}}&{{a_z}} \end{array}} \right]$ 为旋转矩阵，a =[a_x a_y a_z]^T是z_w轴在相机坐标系x_c-O-y_c-z_c中的方向向量；p =[p_x p_y p_z]^T为世界坐标系x_w-O_w-y_w-z_w的坐标原点在相机坐标系x_c-O-y_c-z_c中的平移量^[17-18]。

3.2 环形激光结构光系统

为测量工件在变换平台上的姿态，采用圆结构光激光器、相机构成结构光系统，如图 6所示。图 6a为激光结构光视觉测量原理及相机与激光器之间的几何安装结构；图 6b为相机与激光投射器的整体几何模型。为保证激光投射器轴线与摄像机的光轴平行，采用特制的安装底板，将相机与激光器分别固定在底板的两侧，保证二者之间的几何尺寸。

Figure 6. a—geometric installation structure b—geometric installation model

下载: 全尺寸图片幻灯片

图 6中，相机光轴与激光圆环轴心间距为L，圆环激光出射半角为θ₀，相机物距为H，激光投射器在工件表面投影为圆环形结构光条，半径为r，并有:

$r = H\tan {\theta _0}$

(9)

在构建相机与激光投射器相对位置时，要保证激光圆环在视场范围内，要求相机光轴与激光圆环轴心间距L满足:

$L < S \times H/\left( {2f} \right) - H\tan {\theta _0}$

(10)

式中，S为镜头靶面尺寸，f为镜头焦距。

空间工件的姿态由横滚角、俯仰角和偏转角3个自由度确定。设n_w=(n_{w, x}, n_{w, y}, n_{w, z})为空间工件表面的法向量，根据几何三角关系可推算出工件的姿态参量横滚角θ、俯仰角φ和偏转角ξ：

$\left\{ \begin{array}{l} \theta = {90^ \circ } - \left| {\arctan \left( {{n_{{\rm{w}},z}}/{n_{{\rm{w}},y}}} \right)} \right|\\ \theta = {90^ \circ } - \left| {\arctan \left( {{n_{{\rm{w}},z}}/{n_{{\rm{w}},x}}} \right)} \right|\\ \zeta = \arctan \left( {{n_{{\rm{w}},y}}/{n_{{\rm{w}},x}}} \right) \end{array} \right.$

(11)

激光圆环光条中心坐标(x₀′, y₀′, z₀′)及光条法向量n′=(n_x′, n_y′, n_z′)分别为：

$\left\{ \begin{array}{l} \left( {{{x'}_0},{{y'}_0},{{z'}_0}} \right) = \left[ {r\sqrt {\frac{{\left| {{\lambda _3}} \right|\left( {\left| {{\lambda _1}} \right| - \left| {{\lambda _2}} \right|} \right)}}{{\left| {{\lambda _1}} \right|\left( {\left| {{\lambda _1}} \right| + \left| {{\lambda _3}} \right|} \right)}}} ,} \right.\\ \left. {0,r\sqrt {\frac{{\left| {{\lambda _1}} \right|\left( {\left| {{\lambda _2}} \right| + \left| {{\lambda _3}} \right|} \right)}}{{\left| {{\lambda _3}} \right|\left( {\left| {{\lambda _1}} \right| + \left| {{\lambda _3}} \right|} \right)}}} } \right]\\ \left[ {\begin{array}{*{20}{c}} {{{n'}_x}}&{{{n'}_y}}&{{{n'}_z}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} { \pm \sqrt {\frac{{\left( {\left| {{\lambda _1}} \right| - \left| {{\lambda _2}} \right|} \right)}}{{\left( {\left| {{\lambda _1}} \right| + \left| {{\lambda _3}} \right|} \right)}}} }&0&{ - \sqrt {\frac{{\left( {\left| {{\lambda _2}} \right| + \left| {{\lambda _3}} \right|} \right)}}{{\left( {\left| {{\lambda _1}} \right| + \left| {{\lambda _3}} \right|} \right)}}} } \end{array}} \right] \end{array} \right.$

(12)

式中，λ₁, λ₂, λ₃为矩阵的特征值，r为圆结构光投射在工件表面的半径^[19-20]。

4. 工件端面姿态测量

实验时，将工件置于姿态变换实验平台上，调节姿态变换平台的3个姿态角参量进行测量，如图 7a所示。图 7b为采集的3种不同姿态的工件图像。图 7c为利用阈值分割及形态学膨胀处理方法将激光环形光条区域从工件图像中分割出来。对结构光光条区域应用Hessian矩阵提取结构光光条中心的亚像素坐标，再利用最小二乘椭圆拟合法将转换到成像平面坐标系中的亚像素中心坐标拟合成椭圆方程，见图 7d。最后由椭圆拟合结果测算工件姿态。

Figure 7. Image acquisition and processing for circular laser stripe

下载: 全尺寸图片幻灯片

被测工件的姿态参量(θ, φ, ξ)实验测量值如表 2所示。经实验可得姿态角的测量值与给定值间的平均误差为：姿态参量的横滚角θ平均误差0.373°，俯仰角φ平均误差0.253°，偏转角ξ平均误差0.673°。

Table 2. Measurement results for workpiece attitude

No.	given value (θ, φ, ξ)/(°)	normal vector	measured value (θ, φ, ξ)/(°)
1	(2.0, 5.0, 20.0)	(0.0831, 0.0314, 0.9965)	(1.80, 4.76, 20.69)
3	(3.0, 4.0, 35.0)	(0.0687, 0.0491, 0.9964)	(2.82, 3.94, 35.55)
5	(5.0, 3.0, -60.0)	(-0.0442, 0.0742, 0.9960)	(4.26, 2.54, -59.22)

下载: 导出CSV

| 显示表格

图 8为工件在实验台上给定的姿态角及实际测量的姿态角及对应点的测量误差。从实验结果看，被测工件的姿态测量值与真实值基本相同，但存在一定误差，影响姿态测量结果的误差来源于摄像机与圆结构光投射器之间的支架误差、结构光光条中心亚像素坐标的提取误差等。

a—(θ, φ, ξ)=(2.0, 5.0, 20.0) b—(θ, φ, ξ)=(3.0, 4.0, 35.0) c—(θ, φ, ξ)=(5.0, 3.0, -60.0)

Figure 8. The given attitude angle and the actual measurement angle

下载: 全尺寸图片幻灯片

图 9为工件位移测量原理。图中O为激光结构光几何中心，l₁, l₂分别为点O到参考点1所在边的相对位移。若参考点1不在y轴右侧，则测量点O到参考点2所在边的相对位移。

Figure 9. Relative displacement measurement for workpiece

下载: 全尺寸图片幻灯片

5. 结论

在实验室环境下搭建了六自由度姿态变换实验平台，为了建立姿态变换实验平台的机构模型及视觉系统模型，实现工件变姿态的视觉识别与测量，完成了如下主要工作：分析了机器人关节变换D-H建模原理基础上，构建了六自由度模拟平台的D-H运动学模型，导出了六自由度姿态变换平台的D-H参量表，并求出了实验平台基座到平台末端总的变换矩阵；应用小孔成像原理，建立了六自由度姿态变换平台视觉系统模型，为基于变换实验平台的工件姿态测量奠定了基础。

对激光环形光条图像进行在成像平面的数学表达式推导，得到了工件表面在摄像机坐标系中的法向量，通过坐标系之间的转换得到工件表面在世界坐标系中的法向量，进而推算出工件的姿态参量横滚角θ、俯仰角φ和及偏转角ζ。实验结果表明，3个姿态角的测量值平均误差均小于1°，被测工件的姿态测量值与真实值基本相同。

Figure 1. Schematic of the proposed absorber

a—the designed plasma resonators (top layer) b—the side view c—periodic arrangement of the proposed absorber

下载: 全尺寸图片幻灯片

Figure 2. Absorption curves of designed absorber

a—absorption curve excited by Ω-shaped and square shaped resonators b—absorption curve excited by two U-shaped resonator c—absorption curve excited by all resonators

下载: 全尺寸图片幻灯片

Figure 3. a—the distributions of electric field at 9.24GHz b—the distributions of surface current at 9.24GHz c—the distributions of electric field at 9.45GHz d—the distributions of surface current at 9.45GHz e—absorption curve of different dielectric substrates

下载: 全尺寸图片幻灯片

Figure 4. a—absorption curves for g=0.5mm, 0.6mm, 0.7mm, 0.8mm b—the diagram of g vs.A c—absorption curves for d=6.8mm, 7mm, 7.2mm, 7.4mm d—the diagram of d vs. A

下载: 全尺寸图片幻灯片

Figure 5. Schematic and absorption curve of the proposed band enhanced absorber

a—schematic of plasma resonators (top layer) b—the side view c—the simulated absorption curve

下载: 全尺寸图片幻灯片

Figure 6. a—the distributions of electric field at 12.32GHz b—the surface current of bottom metallic plate at 12.32GHz

下载: 全尺寸图片幻灯片

Figure 7. a—absorption curves for s=1.3mm, 1.5mm, 1.7mm, 1.9mm b—the diagram of s vs. A

下载: 全尺寸图片幻灯片

Figure 8. a—absorption curves for φ=0°, 10°, 20°, and 30° b—the diagram of φ vs. A

下载: 全尺寸图片幻灯片

Table 1 The variables of the proposed absorber

variable	X	B	C	d	E	F	g	H	L	M	N	O	P	Q	R	W
value/mm	45	0.8	14.96	7	1.38	8.54	0.8	3.6	36	6.42	6.4	0.79	25.98	7.98	8.5	0.0138

下载: 导出CSV

参考文献(26)

[1]	HATAKEEYYAMA K, INUI T. Electromagnetic wave absorber using ferrite absorbing material dispersed with short metal fibers[J]. IEEE Transactions on Magnetics, 1984, 20(5):1261-1263. DOI: 10.1109/TMAG.1984.1063424
[2]	LIMA U R, NASAR M C, NASAR R S, et al. Ni-Zn nanoferrite for radar-absorbing material[J]. Journal of Magnetism & Magnetic Materials, 2008, 320(10):1666-1670. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8e6da0162397a84f96163cc9464d983c
[3]	MARIN P, CORTINAD, HERNANDO A. Electromagnetic wave absorbing material based on magnetic microwires[J]. IEEE Transactions on Magnetics, 2008, 44(11):3934-3937. DOI: 10.1109/TMAG.2008.2002472
[4]	HODGKINSON I, WU Q H. Inorganic chiral optical materials[J]. Advanced Materials, 2001, 13(12/13):889-897. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0221676448/
[5]	SIONCKE S, VERBIEST T, PERSOOONS A. Second-order nonlinear optical properties of chiral materials[J]. Materials Science and Engineering, 2003, R42(5/6):115-155.
[6]	SHIM J M, SHAN S C, KOŠMRLJ A, et al. Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials[J]. Soft Matter, 2013, 9(34):8198-8202. DOI: 10.1039/c3sm51148k
[7]	WANG J F, QU Sh B, MA H, et al. Tunable planar left-handed metamaterials based on split-ring resonator pairs[C]//IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications. New York, USA: IEEE, 2015: 1-3.
[8]	ZHOU H, WANG C, PENG H. A novel double-incidence and multi-band left-handed metamaterials composed of double Z-shaped structure[J]. Journal of Materials Science Materials in Electronics, 2016, 27(3):2534-2544. DOI: 10.1007/s10854-015-4056-2
[9]	LIU S H, GUO L X, LI J Ch. Left-handed metamaterials based on only modified circular electric resonators[J]. Journal of Modern Optics, 2016, 63(21):2220-2225. DOI: 10.1080/09500340.2016.1189008
[10]	RYBIN O, SHULGA S. Profile miniaturization and performance improvement of a rectangular patch antenna using magnetic metamaterial substrates[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2016, 26(3):254-261. DOI: 10.1002/mmce.v26.3
[11]	ZHANG Y, TANG H, YAO Ch, et al. Experiments on adjustable magnetic metamaterials applied in megahertz wireless power transmission[J]. AIP Advances, 2015, 5(1):2075-2084.
[12]	KIRIUSHECHKINA S V, KOTEI'NIKOVA O A, RADKOVSKAYA A A. Peculiarities of propagation of electroinductive waves in magnetic metamaterials[J]. Physics of Wave Phenomena, 2017, 25(2):101-106. DOI: 10.3103/S1541308X17020042
[13]	TARKHANAYAN R H. Effective permittivity and permeability of magnetic metamaterials with periodic array of 2-D electronic layers in quantum hall effect conditions[J]. Journal of Electromagnetic Waves & Applications, 2008, 22(7):1005-1012.
[14]	WANG R L, WANG J F, LI Y F, et al. Dual-band suspended stripline filter based on electric metamaterials[J]. Microwave & Optical Technology Letters, 2017, 59(9):2297-2302. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=57f61e66266c3b5e858a96811c8daf1f
[15]	WEI Y Sh, SU AN, XU J Y, et al. Characteristics of dual-channel optical filter in quaternary heterostructure photonic crystal [J]. Laser Technology, 2018, 42(2): 212-212(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgjs201802014
[16]	ZHANG X D, CHEN N, NIE F K, et al. Dispersion characteristics analysis of photonic crystal fibers based on structure parameters and filling modes [J]. Laser Technology, 2018, 42(1):48-52 (in Chinese).
[17]	LANDY N I, SAIUYIGBE S, MOCK J J, et al. Perfect metamaterial absorber[J]. Physical Review Letters, 2008, 100(20): 207402. DOI: 10.1103/PhysRevLett.100.207402
[18]	ZHANG H, ZHANG H F, YANG J, et al. Design of an absorber based on plasma metamaterial[J]. Laser Technology, 2018, 42(5): 704-708(in Chinese).
[19]	WU D, LIU Y, LI R, et al. Infrared perfect ultra-narrow band absorber as plasmonic sensor [J]. Nanoscale Research Letters, 2016, 11(1):483-491. DOI: 10.1186/s11671-016-1705-1
[20]	WANG B X, WANG L L, WANG G Z, et al. Theoretical investigation of broadband and wide-angle terahertz metamaterial absorber[J]. IEEE Photonics Technology Letters, 2014, 26(2): 111-114. DOI: 10.1109/LPT.2013.2289299
[21]	LI L, WANG J, DU H, et al. A band enhanced metamaterial absorber based on E-shaped all-dielectric resonators[J]. AIP Advances, 2015, 5(1): 017147. DOI: 10.1063/1.4907050
[22]	DING F, CUI Y, GE X, et al. Ultra-broadband microwave metamaterial absorber[J]. Applied Physics Letters, 2012, 100(10):103506. DOI: 10.1063/1.3692178
[23]	CHENG Y Zh, WANG Y, NIE Y, et al. Design, fabrication and measurement of a broadband polarization-insensitive metamaterial absorber based on lumped elements[J]. Journal of Applied Physics, 2012, 111(4): 044902. DOI: 10.1063/1.3684553
[24]	KONG X K, LI H M, BIAN B R, et al. Microwave tunneling in heterostructures with electromagnetically induced transparency-like metamaterials based on solid state plasma[J]. The European Physical Journal Applied Physics, 2016, 74(3): 30801. DOI: 10.1051/epjap/2016150452
[25]	KONG X K, MO J J, YU Zh Y, et al. Reconfigurable designs for electromagnetically induced transparency in solid state plasma metamaterials with multiple transmission windows[J]. International Journal of Modern Physics, 2016, B30(14): 1650070. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8f696b59cdea7d584b0e345e18fe189c
[26]	BALANIS C A. Antenna theory: analysis and design[M].Hoboken, New Jersey, USA:John Wiley & Sons, 1982:989-990.

施引文献

资源附件(0)

图(8) / 表(1)

计量

文章访问数: 3
HTML全文浏览量: 1
PDF下载量: 5
被引次数: 0

引言
1. 六自由度姿态变换实验平台原理
2. 六自由度姿态变换实验平台模型
2.1 机器人关节变换的D-H建模原理
2.2 六自由度模拟平台D-H运动学模型
3. 六自由度姿态变换平台视觉系统模型
3.1 小孔成像模型
3.2 环形激光结构光系统
4. 工件端面姿态测量
5. 结论

引言
1. 六自由度姿态变换实验平台原理
2. 六自由度姿态变换实验平台模型
2.1 机器人关节变换的D-H建模原理
2.2 六自由度模拟平台D-H运动学模型
3. 六自由度姿态变换平台视觉系统模型
3.1 小孔成像模型
3.2 环形激光结构光系统
4. 工件端面姿态测量
5. 结论

参考文献(26)

施引文献

资源附件(0)

一种带宽展宽的等离子体超材料吸波体的设计

作者简介:
张浩(1996-), 男, 大学本科生, 现主要从事超材料吸波器、电磁超材料的研究

通讯作者:
章海锋, E-mail:hanlor@163.com

计量

Design of a band enhanced absorber based on plasma metamaterial