引言

在高能激光技术领域，紧凑型、轻量化和多平台化是未来发展趋势^[1]。目前，连续工作方面主要采用光纤激光器，因其增益介质的表面积比大、散热性能好，而在脉冲工作方面尚未找到较为理想的工作介质。自从高功率激光半导体出现并成为固体激光器的抽运源以来，掺镱(Yb³⁺)离子激光晶体材料备受关注。因为Yb离子的f主态内唯一的吸收带与铟镓砷二极管的发射带重合，能够实现有效耦合，而且不存在上转换和激发态吸收^[2-5]。其中掺镱钇铝石榴石(Yb ∶Y₃Al₅O₁₂, Yb ∶YAG)是应用最为广泛的Yb激光晶体材料。然而，Yb ∶YAG的荧光寿命较长、发射截面较小，这限制了它在高能脉冲型激光器中的应用。

截至目前为止，国内外学者在实验上对Yb ∶YAG晶体的研究非常广泛，但是对其系统性的理论解释和预测的研究却较少。有部分研究者基于第一性原理对Yb ∶YAG晶体自身的结构和光学性质进行了仿真计算和预测，与实验测试吻合得较好^[6]，但是并没有对不同掺杂稀土离子的Yb ∶YAG晶体进行理论计算方面的研究，更不用说以掺杂改性为手段进行激光性能优化的仿真计算研究。中国科学院上海光学精密机械研究所、中国工程物理研究院、西南技术物理研究所等单位均开展了通过掺杂调控配方抑制薄片Yb ∶YAG晶体自发辐射放大的相关研究，中国科学院上海硅酸盐所开展了通过掺杂调控氟化钙(Yb ∶CaF₂)晶体激光性能的研究，但未见通过调控Yb ∶YAG晶体性能实现高能脉冲应用的报道。

本文作者基于第一性原理对不同掺杂种类/浓度稀土离子的Yb ∶YAG晶体进行模拟计算，获得多种掺杂晶体配方, 然后尝试共掺恰当的稀土离子到Yb ∶YAG晶体中, 通过调节晶体场、电荷平衡度、不同格位等方式来影响Yb³⁺离子4f壳层电子，随后进行晶体生长实验和性能测试验证，从而达到通过配方设计来调控Yb ∶YAG晶体荧光性能的目的。这项工作对于今后高能固体激光器发展具有重要基础性意义。

1.   模拟计算

1.1   概述

目前，稀土掺杂无机材料的理论计算已经获得很大的发展，各种方法也层出不穷。SUN等人在最近发表的综述文章中回顾了传统晶体场理论以及近些年发展起来的第一性原理计算方法^[7]。稀土掺杂材料的跃迁主要包括基质价带和导带跃迁、稀土离子内的电子跃迁和电荷迁移跃迁^[8]。对于第一类跃迁的理论描述，关键在于如何准确处理基质晶体材料的电子能带结构。近年来发展了多种理论方法，例如基于密度泛函理论的修正贝克-琼斯势方法^[9-10]、密度泛函理论(density functional theory+U, DFT+U)方法^[11-12]、杂化泛函方法^[13]、基于格林函数多体微扰理论的格林函数(Green wave, GW)方法^[14-16]，以及第一性原理的计算被用在Ce(La) ∶YAG^[17]、Ce(Eu) ∶Li₂SrSiO₄^[18]等材料的电子结构和光学跃迁机制的研究。利用上述修正后的DFT方法虽然能够比较准确地计算出基质材料的电子能带结构以及带隙，但是对描述第2类跃迁还存在一定困难。当下稀土离子4f^N组态内的光谱学理论研究和计算已经较为成熟，基于晶体场理论的光谱拟合随着计算机技术的发展逐渐在不同体系中得到验证。

1.2   模拟计算原理及方法

根据晶体中稀土离子的光谱理论和Judd-Ofelt(J-O)理论，晶体中稀土离子的辐射寿命τ_r表示为^[19]：

式中, $A\left(J^{\prime} ; J\right)$为上激发态能级$J^{\prime}$到下能级$J$的辐射跃迁速率, 又可以表示为^[20]：

式中, $e$为电子电荷量; $\varepsilon_{0}$为真空介电常数; $h$为普朗克常数; $n$为基质晶体的折射率; $g_{J}$为跃迁初态$J^{\prime}$能级的简并度; $\bar{\lambda}$是辐射电磁波的平均波长; $S_{\mathrm{ED}}$为电偶极(electric dipole, ED) 跃迁谱线强度; $S_{\mathrm{MD}}$为磁偶极(magnetic dipole, MD) 跃迁谱线强度。一般来说, $S_{\mathrm{ED}}$比$S_{\mathrm{MD}}$大, 但是某些稀土离子部分能级之间的磁偶极跃迁也可以达到与电偶极跃迁相比拟的程度。因此, $S_{\mathrm{ED}}$又可写为标准的J-O理论三参量形式^[19]：

式中，Ω_λ即为J-O参量，$f^{N}$表示稀土离子的$4 f^{N}$壳层, $S$和$L$分别表示晶体中稀土离子的总自旋角动量和总轨道角动量, $S^{\prime}$和$L^{\prime}$与之含义相同, 但是取值不同, $\boldsymbol{U}^{(\lambda)}$为$\lambda$阶单位张量算符。

从(1)式~(3)式可以看出：欲减少Yb ∶YAG晶体中Yb离子的辐射/荧光寿命。在基质YAG确定、折射率n也确定的情况下，只有提高S_ED的大小，即增大J-O参量Ω_λ的方法。此外，增大Ω_λ也可以同时增大发射截面, 另外注意到，J-O参量Ω_λ可以表示为：

式中, $A_{t, p, \lambda}$为奇次晶场参量; $t$的取值可以为$\lambda \pm 1$, 亦即1, 3, 5, 7;p的取值范围为-t~t，具体与研究体系点群对称有关; $\mathit{\Xi}$是一个只与$t$和$\lambda$有关的因子，具体定义参见参考文献[21]。可见，J-O参量$\mathit{\Omega}_{\lambda}$取决于奇次晶场参量的大小, 其值越大, 与$4 f^{N}$组态宇称相反的$4 f^{N-1} 5 d$组态混人初态和终态波函数的成分越大, 电偶极跃迁就会越强。故需要增强$\mathrm{Yb}^{3+}$离子在$\mathrm{YAG}$晶体中受到的晶体场相互作用。

晶场参量描述了中心金属离子(这里为Yb³⁺离子)在基质晶体中(这里为YAG晶体)受到周围配体离子的各种复杂的相互作用。欲计算稀土离子的光谱特性，需要借助量子力学的方法。描述一个稀土离子在晶体中的哈密顿量H可以写为:

式中, $H_{\text {free }}$为自由离子项, 对$\mathrm{Yb}^{3+}$来说, 就是其$4 f^{13}$组态电子的自旋-轨道耦合作用(用旋轨耦合系数$\zeta$表征); $H_{\mathrm{CF}}$就是晶体场(crystal field, CF) 作用项, 其形式取决于中心离子及其周围配体的点群对称。对$\mathrm{Yb}$ : $\mathrm{YAG}$晶体, 一般认为$\mathrm{Yb}^{3+}$进人晶体后取代$\mathrm{Y}^{3+}$的格位, 其点群对称为$D_{2}$, 该对称下的$H_{\mathrm{CF}}$形式为^[22]：

式中, $B_{k, q}(k=2, 4, 6 ; q=-k, -k+1 \cdots, k-1, k)$即为晶场参量; $\boldsymbol{C}_{k, q}$为相应的球张量算子。选定一组基函数后(稀土离子常取$L-S$耦合的波函数$\left|L S J M_{J}\right\rangle$), 对角化(5) 式的哈密顿能量矩阵就可以求得晶场能级和对应的晶场波函数，晶场能级之间的跃迁就是实验测定的光谱线位置，晶场波函数则可以用来计算跃迁强度。一般来说，(6)式中的晶场参量可以通过拟合各种实验数据，如光谱、电子顺磁共振(electron paramagnetic resonance，EPR)、光探测磁共振谱(optically detected magnetic resonance，ODMR)，甚至磁化率等来获得。对于没有任何实验数据的情况，就需要采用第一性原理方法计算。

晶场参量的大小显然与中心离子到周围配体的距离和配体离子的空间构型有关。采用重叠模型近似，可以将晶场参量表示为：

式中, $\bar{B}_{k}\left(R_{0}\right)$为内禀晶场参量; $R_{i}$为第$i$个配体到中心离子的距离; $K_{k, q}$为第$i$个配体的坐标因子; $t_{k}$为指数律因子, 可以通过拟合光谱获得, 也可以取固定值; $\varphi_{i}$和$\theta_{i}$分别为第$i$个配体在选定坐标系里面的球坐标。注意(7) 式对奇次晶场参量$A_{t, p, \lambda}$也成立。

要改变/调控(7)式的晶场参量值(广义上可称为“晶体场工程”)，一种方法是改变内禀晶场参量$\bar{B}_{k}\left(R_{0}\right)$, 但该值大部分取决于中心离子和配体的化学键性质，配体如果不变，难以调控；另外的方法是改变配体的空间构型，这相对容易实现。本文中提出的共掺离子方法，本质就是改变中心离子周围的配体局部结构来达到改变晶场参量的目的。当然，还需要对YAG晶体的本征缺陷(空位、反位等)有所了解。

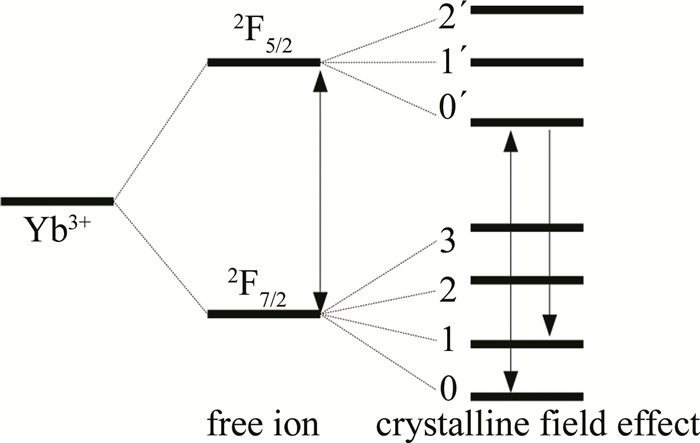
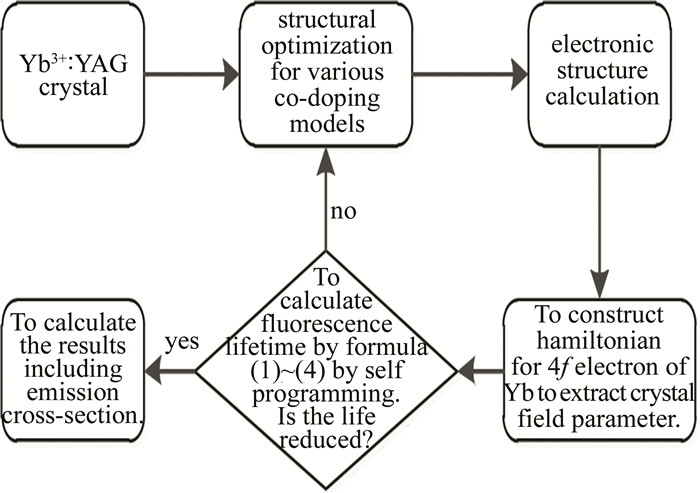
通过以上分析，本文中通过共掺离子方式来调控YAG晶体中Yb³⁺离子所受晶场强度的理论方案，示意图如图 1所示。

图  1  模拟计算方案示意图

Figure  1.  Sketch map of simulation scheme

下载: 全尺寸图片 幻灯片

1.3   结构优化

采用了密度泛函的PBE(Perdew-Burke-Emzerhof)方法对纯YAG和掺杂原子数分数为5%的Yb ∶YAG的结构进行了优化。布里渊区的K点网格的密度为2×2×2。纯YAG和掺杂原子数分数为5%的Yb ∶YAG优化后的晶格参数见表 1。可以看到，纯YAG的晶格常数为1.20119 nm，比实验测得的1.2003 nm略高(小于1%)，这是由于软件的固有缺点造成的，是可以接受并且合理的。另外注意到，掺杂Yb离子之后的晶格矢量有微量的变化，这种因为少量替换引起的晶格膨胀和角度变化可以忽略不计(小于0.1%)，之后电子特性的计算都是在此结构优化的基础上来进行的。

表  1  结构优化后的晶格常数

Table  1.  Lattice constants after structure optimization

	YAG	Yb∶YAG
a/nm	(1.20119，0.00000，0.00000)	(1.20115，0.00000，0.00034)
b/nm	(0.00000，1.20119，0.00000)	(0.00000，1.20079，0.00000)
c/nm	(0.00000，0.00000，1.20119)	(0.00034，0.00000，1.20115)
α/(°)	90.0000	90.0000
β/(°)	90.0000	89.9675
γ/(°)	90.0000	90.0000

下载: 导出CSV 

| 显示表格

在上一步结构优化的基础上，通过对电荷密度的计算获得了各个键长数据，见表 2。计算中修改了INCAR文件里的IBRION=1，即离子位置优化算法为分子动力学模拟；修改NSW=0，停止离子位置优化，最大优化步骤为0。发现在电荷分布方面，纯YAG晶体Y³⁺—O^2-之间电荷分布更加均匀，共价键的键性更大，而Yb ∶YAG的Yb³⁺—O^2-之间电荷分布较YAG晶体相比更加不均匀，离子键的键性更大。另外，从化学键的长度方面来说，纯YAG晶体的Y³⁺—O^2-的长度为0.24318 nm，而Yb ∶YAG的Yb³⁺—O^2-的长度为0.24607 nm，所以YAG晶体的Y³⁺—O^2-的长度更短，Yb ∶YAG的Yb³⁺—O^2-的长度更长，也可以证实YAG晶体的Y³⁺—O^2-更趋向于共价键，Yb ∶YAG的Yb³⁺—O^2-的键性更趋向于离子键；在Cr⁴⁺共掺杂Yb ∶YAG晶体中，几种化学键的长度又有所变化，其中Y³⁺—O^2-的长度为0.2309 nm，与纯YAG晶体以及Yb ∶YAG晶体相比键长变短，Yb³⁺—O^2-的长度为0.24576 nm，这与Yb ∶YAG晶体相比也有所减小，这都与Cr⁴⁺的掺杂有关，在Cr⁴⁺共掺的Yb ∶YAG晶体中，Al³⁺—O^2-(四面体)键的长度为0.17727 nm，而Cr⁴⁺—O^2-(四面体)的长度为0.17714 nm, 二者相差无多，而在纯YAG晶体中Al³⁺—O^2-(四面体)键的长度为0.17723 nm，综合来说，这可能是因为虽然Cr⁴⁺离子的半径较大，但是Cr的原子序数较高，使得Cr⁴⁺—O^2-(四面体)的键长较短，由于Cr⁴⁺的离子半径比Al³⁺大得多，对晶格产生了挤压效应，使得Yb³⁺—O^2-的键长以及Y³⁺—O^2-的键长略微缩短。

表  2  3种类型键的长度

Table  2.  Three types of bond lengths

	type	bond length/nm
YAG	Y3+—O2-	0.24318
	Al3+—O2-(tetrahedron)	0.17723
Yb∶YAG	Y3+—O2-	0.22879
	Yb3+—O2-	0.24607
Cr, Yb∶YAG	Y3+—O2-	0.23090
	Yb3+—O2-	0.24576
	Al3+—O2-(tetrahedron)	0.17727
	Cr4+—O2-(tetrahedron)	0.17715

下载: 导出CSV 

| 显示表格

1.4   电子态密度计算

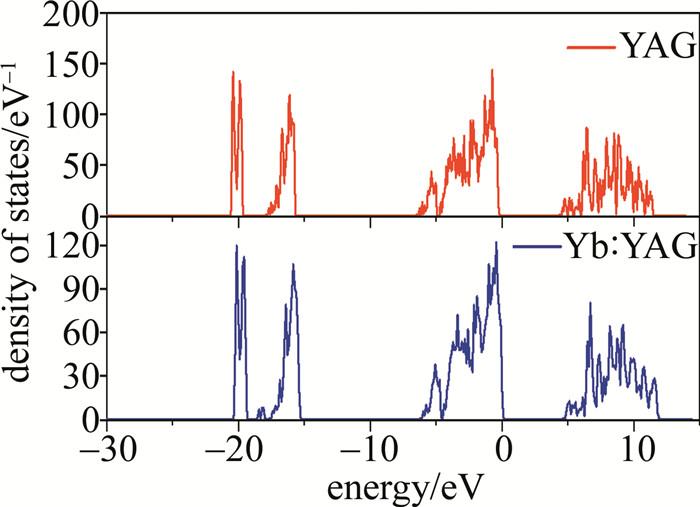
在优化了结构的基础上，采用软件计算了纯YAG和掺杂原子数分数为5%的Yb ∶YAG电子结构。根据计算，YAG电子态密度图的如图 2所示。计算出来的钇铝石榴石的禁带宽度为4.8 eV，而光学测量的带隙为6.5 eV，计算结果略低。这个结果是由于软件的算法造成的，在其它的氧化物中也发现了类似的结果，该软件计算时采用平面波基组的方法，平面波在能带边缘的奇偶同性，会造成计算的禁带宽度略小。掺杂Yb离子原子数分数为5%的YAG电子特性较纯YAG晶体来说并没有太大改变。

图  2  YAG和Yb ∶YAG的总电子态密度图

Figure  2.  Total density of states(TDOS) of YAG and Yb ∶YAG

下载: 全尺寸图片 幻灯片

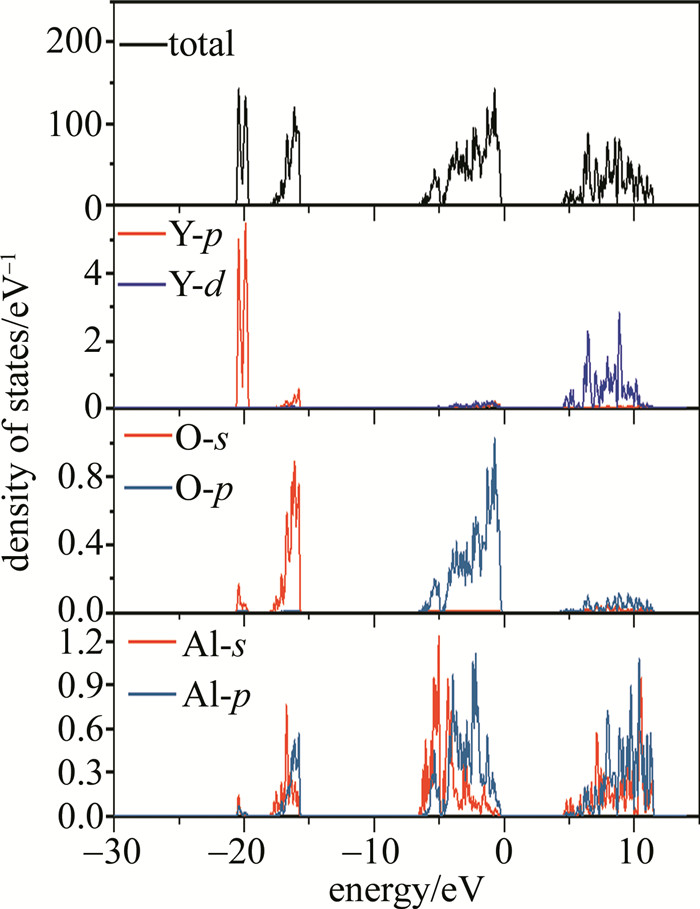
从YAG的分态密度图(见图 3)可知，不论是氧八面体中心的Al原子，还是氧四面体中心的Al原子，对于总的电子结构贡献很小。而Y原子和O原子对于总的电子态密度有着重要的贡献。Yb晶体的价带主要是由O原子的2p轨道的电子所贡献的，而导带则主要是由Y原子的4d轨道的电子所贡献的；另外，可以观察到Y离子的4d和O离子的2p轨道在价带和导带都存在微弱的杂化，这可能为光电子和热电子的迁移提供了通道^[23]。在总的态密度图中，-16 eV处的峰主要是O原子的2s电子所贡献；-20 eV处的峰主要是Y原子的3p电子态所形成的。一般来说，费米能级附近的能态，对材料的性质有着决定性的作用。

图  3  YAG的分态密度图

Figure  3.  Partial density of states (PDOS) of YAG

下载: 全尺寸图片 幻灯片

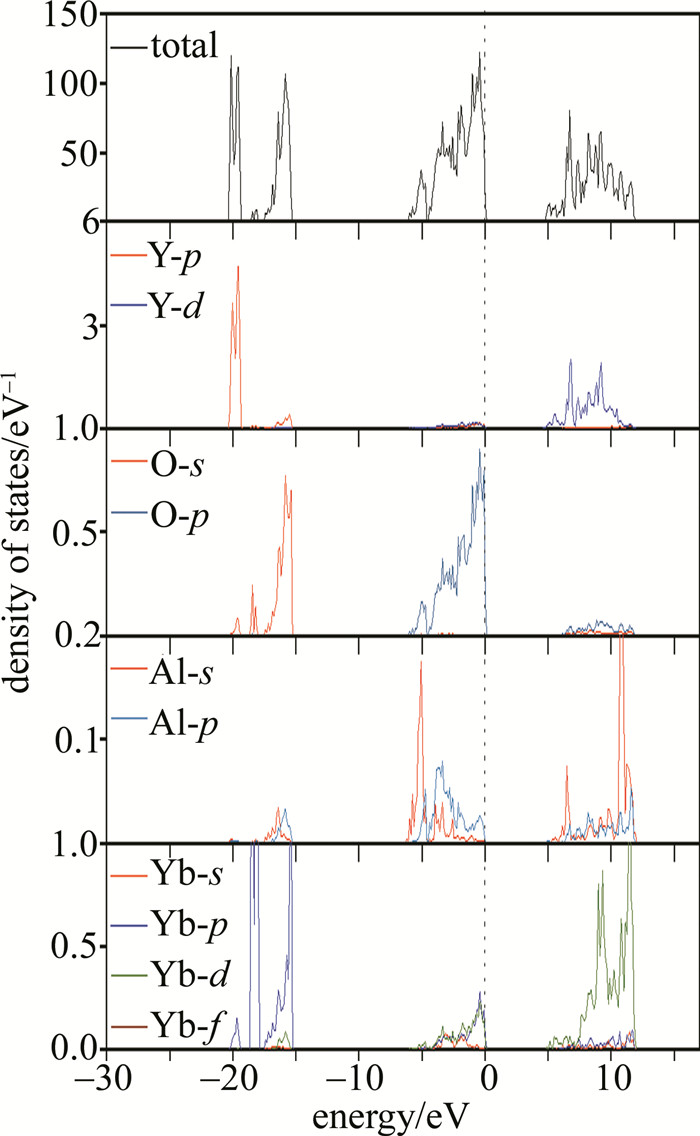
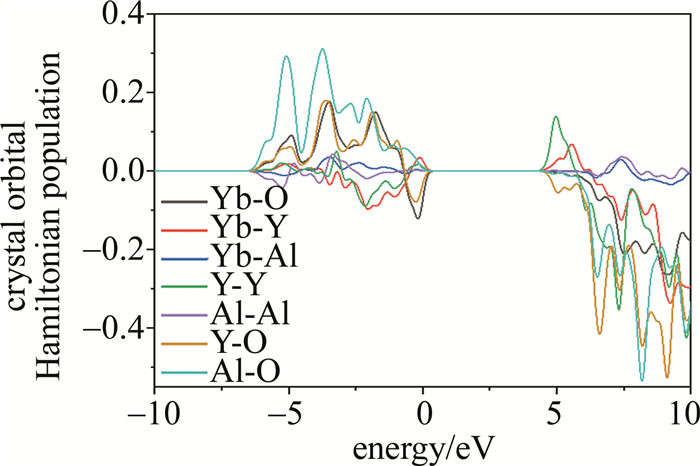
从图 3可看出，Al原子对于总态密度贡献很小，所以，Al原子对于YAG晶体有稳定结构的作用。YAG的导带几乎上由Y离子的4d电子态构成，表明了Y原子是可以被替换的。而价带由O原子的2p电子态贡献，也就是说，在YAG晶体结构中，O原子很难被取代。图 4是Yb ∶YAG的分态密度图。少量的Yb离子的掺杂并没有在总电子态密度中产生显著的变化，Yb离子的5p轨道的态密度主要位于价带下方，15 eV处，而Yb离子的5d轨道所对应的能级处于导带当中，并且显示出比Y离子更高的能级，约13 eV，这是因为Yb离子的5d轨道的电子比Y离子的4d轨道的电子能量更高，电负性对较低，这也意味着与外部电子的结合能力较低。另外，Yb离子的6f轨道则几乎无电子态密度分布，这主要是因为6f轨道所对应的电子能量太高，电子进入的可能性低；此外，对于3价的Yb离子，6f轨道是一个空轨道。而掺杂Yb离子之后的Al离子的态密度图在导带11 eV的位置突然出现了一个峰，为了探究这个峰的出现是否由于Yb离子的掺杂引起，计算了Yb ∶YAG的晶体轨道哈密顿布居数，如图 5所示。可以看到，Yb离子与Al离子的轨道交叠维持在较低的水平; 而且，在Yb离子的价带顶大于0 eV时出现了很微小的态密度分布，表现出导体性质，说明Yb离子掺杂后，Yb ∶YAG出现很微弱的导电特性，这也解释了在结构优化时，出现了微弱的磁矩。

图  4  Yb ∶YAG的分态密度图

Figure  4.  PDOS of Yb ∶YAG

下载: 全尺寸图片 幻灯片

图  5  Yb ∶YAG晶体的哈密顿布居数图

Figure  5.  Hamitonian population of Yb ∶YAG

下载: 全尺寸图片 幻灯片

1.5   晶体场参量及荧光寿命计算

为得到未共掺其它离子的$\mathrm{Yb}: \mathrm{YAG}$晶体准确的晶场参量, 首先需要获得$Y b$ : YAG晶体的光谱和$E P R$谱, 再通过拟合数据得到。利用生长制备的$\mathrm{Yb}: \mathrm{YAG}$晶体和$\mathrm{Yb}, \mathrm{Cr}$ : $\mathrm{YAG}$晶体样品准确测试了光谱(详见后面2.2.1节)。利用光谱数据结合EPR谱^[24]进行拟合计算, 得到了$\mathrm{Yb}: \mathrm{YAG}$晶体中处于$D_{2}$对称格位的$\mathrm{Yb}^{3+}$离子的晶场参量为: $B_{2, 0}=-99.2 \mathrm{~cm}^{-1}, B_{2, 2}=277.7 \mathrm{~cm}^{-1}$, $B_{4, 0}=-1941.7 \mathrm{~cm}^{-1}, B_{4, 2}=313.1 \mathrm{~cm}^{-1}, B_{4, 4}=832.2 \mathrm{~cm}^{-1}$, $B_{6, 0}=568.6 \mathrm{~cm}^{-1}, B_{6, 2}=-234.2 \mathrm{~cm}^{-1}, B_{6, 4}=675.1 \mathrm{~cm}^{-1}$, $B_{6, 6}=-15.3 \mathrm{~cm}^{-1}$。

对角化Yb³⁺在YAG中的能量矩阵以后可以得到7个二重简并的Kramers晶场能级波函数(只给出系数大于0.2的波函数)：

上面各等式右边的|7/2, 5/2 〉表示J=7/2和M_J=5/2的量子态，其它以此类推。Yb³⁺离子的各晶场能级及标记，如图 6所示。

图  6  Yb³⁺离子在晶体场中的能级结构

Figure  6.  Energy structure of Yb³⁺ in crystal field

下载: 全尺寸图片 幻灯片

前面已经提及过，稀土离子4f组态内部的晶场能级跃迁强度取决于奇次晶场参量A_{t, p}，由于Yb³⁺占据D₂点群格位，这样独立的奇次晶场参量有：A_{3, 2}，A_{5, 2}和A_{5, 4}^[25]。采用前述重叠模型公式(7)式，引入两个内禀晶场参量A₃和A₅，其中t₃=5, t₅=7^[26]。结合前面获得的Yb³⁺ ∶YAG晶体的掺杂优化结构，通过拟合原子数分数为5%的Yb³⁺ ∶YAG晶体941 nm抽运跃迁截面0.77×10^-20 cm²和1030 nm发射截面2.1×10^-20 cm^2[27], 得到A₃和A₅的值。然后利用这两个值计算出3个激发态晶场能级分别到4个基态晶场能级的总辐射跃迁速率A_i→j及荧光寿命τ的理论计算值(300 K下，根据(1)式和(2)式计算), 计算结果见表 3。需要注意的是：这里磁偶极跃迁也有贡献，应该和电偶极跃迁加在一起算，即总辐射跃迁速率。

表  3  Yb ∶YAG晶体电偶极辐射跃迁速率及荧光寿命的理论计算值

Table  3.  Calculation results of electric dipole transition rate and lifetime in Yb ∶YAG

f-f transition	Ai→j/s-1	τ/ms	τr/ms
|0′〉→|0〉	402.6	2.48
|0′〉→|1〉	145.2	6.89	0.99
|0′〉→|2〉	303.2	3.3
|0′〉→|3〉	156.7	6.38
|1′〉→|0〉	521.5	1.92
|1′〉→|1〉	150.1	6.66	1.26
|1′〉→|2〉	62.2	16.1
|1′〉→|3〉	58.2	17.2
|2′〉→|0〉	246.7	4.05
|2′〉→|1〉	168.7	5.93	1.76
|2′〉→|2〉	46.9	21.31
|2′〉→|3〉	103.7	9.64

下载: 导出CSV 

| 显示表格

Yb ∶YAG晶体典型的激光工作波长1029 nm对应|0′ 〉→ |2 〉跃迁，因此|0′ 〉上能级的辐射寿命0.99 ms对应于实际测量荧光寿命值。

对于共掺离子方法，比如“Yb³⁺加某种3价阳离子”取代YAG中的“Y³⁺和Al³⁺”, 稀土离子之间的相互作用和能量传递是可能存在的，这个和掺杂原子数分数密切相关，也可以通过改变原子数掺杂浓度来调控。为了防止能量传递导致发光猝灭，需要选取能级结构避开Yb³⁺离子发光波段(约1 μm)的共掺离子，这要通过不断计算尝试来判断。

下面考虑Yb和Cr共掺的体系。首先利用软件优化共掺的晶体结构，得到Yb³⁺周围的局部缺陷结构，然后运用图 1中的模拟流程方法，计算出共掺结构体系中Yb³⁺的奇次晶场参量A_{3, 2}，A_{5, 2}和A_{5, 4}，最后计算出Yb, Cr ∶YAG共掺体系的理论荧光寿命，见表 4。

表  4  Yb, Cr ∶YAG晶体总辐射跃迁速率及荧光寿命的理论计算值

Table  4.  Calculation results of electric dipole transition rate and lifetime in Yb, Cr ∶YAG

f-f transition	Ai→j/s-1	τ/ms	τr/ms
|0′〉→|0〉	307.3	3.25	0.93
|0′〉→|1〉	248.3	4.03
|0′〉→|2〉	281.5	3.55
|0′〉→|3〉	241.9	4.13
|1′〉→|0〉	363.8	2.75	0.74
|1′〉→|1〉	331.5	3.02
|1′〉→|2〉	100.6	9.94
|1′〉→|3〉	555.7	1.8
|2′〉→|0〉	610.5	1.64	0.54
|2′〉→|1〉	68.2	14.7
|2′〉→|2〉	896.0	1.12
|2′〉→|3〉	283.4	4.53

下载: 导出CSV 

| 显示表格

从表 4中的理论值可以看出：对Yb共掺Cr的YAG晶体，其|0′ 〉上能级辐射寿命为0.93 ms，相对于未共掺体系确实会减小。

2.   实验与测试

2.1   晶体生长实验

本文作者使用感应加热提拉法单晶炉生长了Yb ∶YAG和Yb, Cr ∶YAG晶体，Yb掺杂原子数分数为5%，Cr掺杂原子数分数为0.006%，选用[111]方向籽晶，使用N₂作为保护气体，同时提高温场径向分布对称性，确保液流温度，避免散射颗粒和生长条纹，提高晶体质量^[28]。

生长出完整的大尺寸的Yb, Cr ∶YAG晶体，晶体两端切开抛光后观察内部质量良好，没有气泡或包裹物等缺陷，晶体直径达70 mm以上，如图 7所示。

图  7  Yb, Cr ∶YAG晶体毛坯

Figure  7.  Yb, Cr ∶YAG blank crystal

下载: 全尺寸图片 幻灯片

针对混合掺杂晶体在缺氧环境中生长会形成的氧空位、较低的Cr⁴⁺掺杂原子数分数、Yb²⁺引起的色心及由于存在由小面造成的核心和应力条纹，必须经过高温精密退火处理^[9]。这在外观颜色上表现为退火前晶体带绿色，退火后将变为无色(Yb ∶YAG)或棕褐色(Yb, Cr ∶YAG)，如图 8所示。样品尺寸为5 mm×5 mm×9 mm，使用该样品进行了透过光谱和荧光性能的测试。

图  8  Yb ∶YAG和Yb, Cr ∶YAG测试样品

Figure  8.  Sample of Yb ∶YAG and Yb, Cr ∶YAG

下载: 全尺寸图片 幻灯片

2.2   测试

2.2.1   透过谱测试

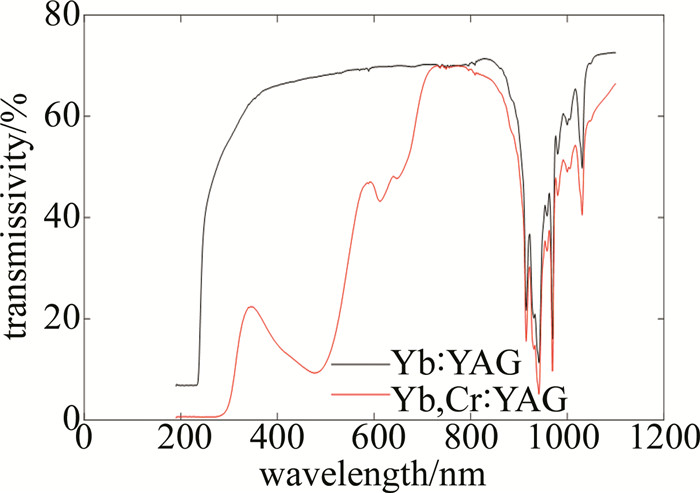
采用λ-900分光光度计测试了Yb ∶YAG晶体和Yb, Cr ∶YAG晶体的透过光谱，测试样品见图 8，结果见图 9。该数据可用于前面第1.5节中晶体场参数的计算。

图  9  Yb ∶YAG晶体和Yb, Cr ∶YAG晶体的透过光谱

Figure  9.  Transmission spectra of Yb ∶YAG and Yb, Cr ∶YAG

下载: 全尺寸图片 幻灯片

2.2.2   荧光测试

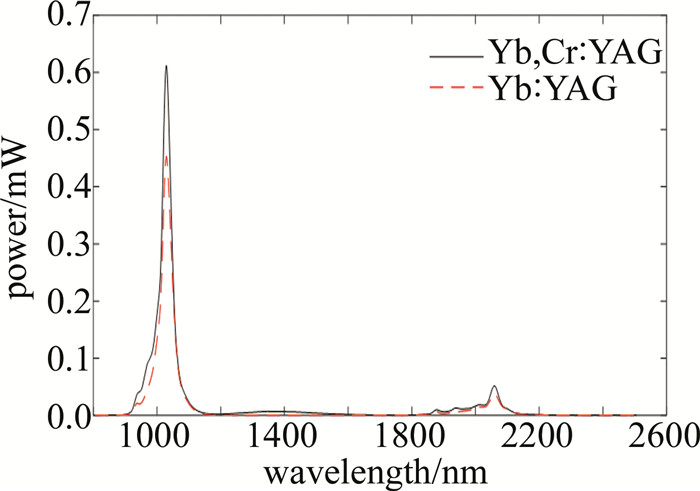
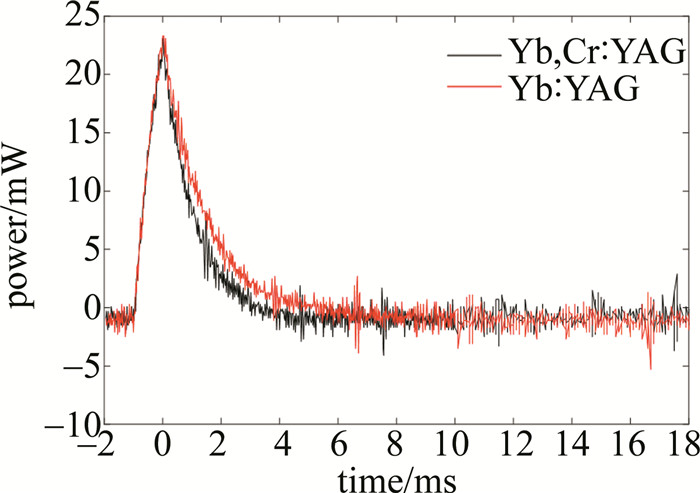
在940 nm激光器激发下测量荧光光谱和荧光寿命。测量荧光光谱时，波长扫描范围800 nm ~2500 nm，激光器工作于脉冲模式用于产生调制信号，样品信号经离轴抛物反射镜反射进入光谱仪、探测器、锁相放大器，最终电脑采集记录下荧光光谱信号。测量荧光寿命时，光谱仪波长固定于1030 nm，激发激光器脉冲频率5 Hz，脉宽1 ms。分别测量了Yb单掺和Yb、Cr双掺YAG晶体的荧光光谱和荧光寿命，结果如图 10、图 11所示。两者的荧光光谱分布非常接近，均在1030 nm和2060 nm附近出现峰值。Yb, Cr ∶YAG荧光寿命曲线衰减更快，寿命更短。通过指数函数$I=I_{0} \exp (-t / \tau)+b$对从脉冲下降沿时刻$0 \mathrm{~ms} \sim 18 \mathrm{~ms}$的数据进行拟合, 拟合参数$\tau$即为苂光寿命。其中$I$表示随时间变化的光强, $I_{0}$表示最大光强, $t$表示时间, $b$表示背景光强。对每个样品进行10次苂光寿命衰减曲线的测量, 对得到的苂光寿命取平均作为荧光寿命值，最终得到Yb, Cr ∶YAG荧光寿命值为0.94 ms，而Yb ∶YAG寿命为1.18 ms。

图  10  荧光光谱测量结果

Figure  10.  Fluorescent spectra measurement results

下载: 全尺寸图片 幻灯片

图  11  荧光寿命测量结果

Figure  11.  Fluorescent lifetime measurement results

下载: 全尺寸图片 幻灯片

3.   结论

本文中成功实现了Yb ∶YAG荧光性能的调控，在第一原理模拟结合晶体场计算结果的方向指导下，通过共掺少量Cr⁴⁺离子后，Yb ∶YAG的荧光寿命从1.18 ms降低至0.94 ms。对Yb ∶YAG和Yb, Cr ∶YAG体系的荧光寿命理论计算值与测量值均较接近，证明作者采用计算方法的正确性。

以上工作不仅能拓展Yb ∶YAG晶体的应用领域，扩大其应用市场，也为高能脉冲激光系统提供了优质的工作物质，突破了限制固体高能脉冲激光技术发展的瓶颈，更重要的是积累了相关科学与技术基础，为其它固体材料拓展应用打开了技术通道。