Effect of initial phase of laser pulse on electron radiation
-
摘要: 为了研究超短超强椭圆偏振激光初始相位对于高能电子辐射特性的影响, 采用了Lorentz方程与电子能量方程构造高能电子与强激光场的对撞模型的方法, 并使用MATLAB进行数值模拟, 获得了电子的运动轨迹以及激光场空间辐射的功率与能量分布的数据与图像, 对不同的激光初始相位所对应的3维空间辐射特性进行了研究。结果表明, 当激光脉冲撞击电子时, 电子产生辐射, 且辐射功率呈现出双峰形; 高能电子的辐射功率图像在初始相位为0°, 180°和360°时表现为对称型双峰, 而在其它相位下则呈现出非对称型双峰。该结论为超短超强椭圆偏振激光的初始相位3维反探测研究提供了一定的基础。Abstract: In order to study the influence of the initial phase of ultrashort and super elliptically polarized laser on the radiation characteristics of high-energy electrons, the collision model of high-energy electrons and high-energy laser field was constructed by Lorentz equation and electron energy equation, and the numerical simulation was carried out by MATLAB. The data and images of electron trajectory and power and energy distribution of spatial radiation of laser field were obtained. The 3-D radiation characteristics corresponding to different initial laser phases were studied. The results show that when the laser pulse strikes the electron, the electron produces radiation, and the radiation power presents a double peak shape. The radiation power image of high-energy electrons shows symmetrical double peaks when the initial phase is 0°, 180° and 360°. The conclusion provides a certain basis for the study of initial phase 3-D inverse detection of ultrashort and ultra strong elliptically polarized laser.
-
引言
自20世纪90年代以来,啁啾脉冲放大技术的出现见证了激光技术的蓬勃发展。如今超短超强激光脉冲的闪亮时间早已达到飞秒[1-2]甚至阿秒[3-6]量级。超短超强激光脉冲的发展在X射线[7-9]、医疗行业[10]和天体物理[11]等研究领域也有着重要的贡献。
在非线性汤姆逊散射[12-14]中,入射激光脉冲的各种参数会影响电子的运动轨迹和辐射特性。例如WANG等人[15]研究了不同脉冲宽度下紧密聚焦圆偏振激光脉冲的非线性汤姆逊散射。LI[16]和WANG[17]等人研究了不同激光强度下圆极化聚焦照射电子的运动和空间辐射特性。YAN等人[18]研究了电子初始位置对高能电子辐射的影响。YU[19]和WU[20]等人研究了不同束腰半径的激光脉冲对电子的影响。而SHI等人[21]发现了在椭圆偏振激光脉冲中,随着脉冲宽度的增加,电子的空间辐射分布有更多的局部极大值集且每组有4个局部极大值。本文作者也是在椭圆偏振激光脉冲的基础上进行研究,但与SHI等人不同的是,本文中研究了超短超强椭圆激光脉冲的初始相位对高能电子运动轨迹和辐射功率空间分布的影响。
作者探讨了高能电子在激光场中的运动,应用Lorentz方程与电子能量方程建立强激光场与单个高能电子的对撞模型,对不同初始相位的椭圆偏振脉冲激光场对撞高能电子所产生的空间辐射功率图像进行模拟,详细讨论了椭圆偏振激光脉冲的初始相位对于高能电子产生辐射功率空间分布的影响,能够通过高能电子辐射功率的空间分布探测出超短超强椭圆偏振激光脉冲的初始相位。
1. 单电子对撞辐射模型
紧聚焦高斯脉冲激光电场的归一化矢势a(η)可以表示为:
\boldsymbol{a}(\eta)=a(\cos \varphi \cdot \boldsymbol{x}+\delta \sin \varphi \cdot \boldsymbol{y}) (1) a=\frac{b_0}{b} a_0 \exp \left(-\frac{\eta^2}{L^2}-\frac{\rho^2}{b^2}\right) (2) 式中,a0=0.85×10-9λ0\sqrt{I}是通过mc2/e进行归一化的激光振幅,其中m和e分别为电子静止时的质量和电量,c是光速,I和λ0为激光强度峰值和激光波长;η=z-t,z和t表示电子在z轴的坐标和观察点的时间;L是激光的脉宽;δ为偏振参量,椭圆偏振下0 < δ < 1;b=b0(1+z2/zR2)1/2为脉冲传播到z轴时的束腰半径;zR=b02/2为瑞利长度;b0是b的最小值;ρ2=x2+y2代表与传播方向的垂直距离,高斯脉冲形状是分别由横向参数exp(-ρ2/b2)和纵向参数exp(-η2/L2)所决定。定义脉冲相位为:
\varphi=c_0 \eta^2+\eta+\varphi_R-\varphi_{\mathrm{G}}+\varphi_0 (3) 式中,φ0是激光脉冲的初始相位;c0为激光啁啾参数;φG=z/zR为古伊相位;φR=ρ2/2R(z)与波前曲率有关,R(z)=z(1+1/φG2)为波前曲率半径。在上述定义中,k0-1和ω0-1已将空间坐标和时间坐标归一化,其中k0和ω0为激光的波数和频率。在库仑定律▽·a=0下,矢场纵向分量为:
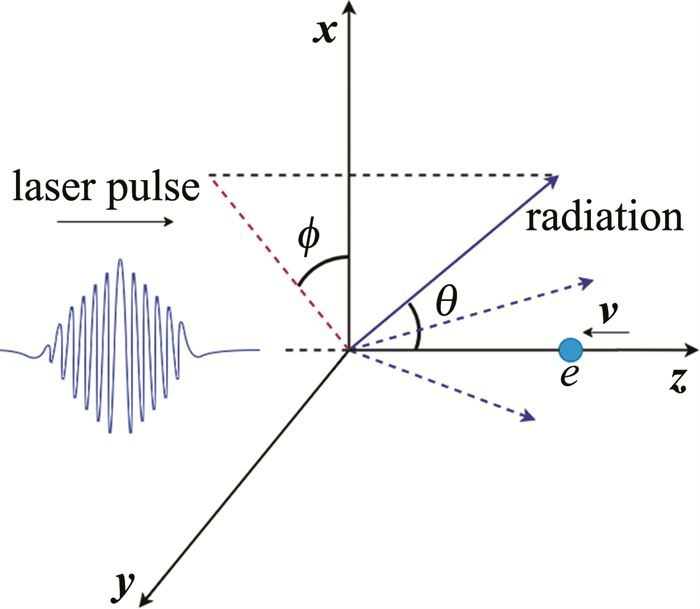
\boldsymbol{a}_z=\frac{2 a[-x \cos (\varphi+\theta)+\delta y \sin (\varphi+\theta)] \boldsymbol{z}}{b_0 b} (4) 式中,θ=π-arctan(z/zR)。椭圆偏振激光脉冲与高能电子相互作用的示意图如图 1所示。
设电子沿着-z轴方向移动,激光脉冲沿z轴正方向移动。在真空激光和单电子理论中,激光场中电场强度E=-da/dt,给出真空中单电子与激光发生碰撞运动的基本方程:
\nabla^2 \boldsymbol{a}+\mathrm{d} \boldsymbol{a} / \mathrm{d} \boldsymbol{u}=0 (5) \mathrm{d}(\boldsymbol{p}-\boldsymbol{a}) / \mathrm{d} t=-\nabla \gamma (6) \mathrm{d} \gamma / \mathrm{d} t=\boldsymbol{u} \cdot(\mathrm{d} \boldsymbol{a} / \mathrm{d} t) (7) 式中,u为电子的速度;p=γu为电子动量; γ=(1-u2)-1/2为电子能量。考虑到:
\nabla \gamma=(\boldsymbol{u} \cdot \nabla) \boldsymbol{p}+\boldsymbol{u} \times(\nabla \times \boldsymbol{a}) (8) 由于矢量势垂直于激光传播方向,电子的速度可以分解为正交分量:
\left\{\begin{array}{l} \gamma\left(\mathrm{d} u_x / \mathrm{d} t\right)=\left(1-u_x{ }^2\right)\left(\mathrm{d} a_x / \mathrm{d} t\right)-u_x u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right)+u_y\left(\mathrm{~d} a_x / \mathrm{d} y-\mathrm{d} a_y / \mathrm{d} x\right) \\ \gamma\left(\mathrm{d} u_y / \mathrm{d} t\right)=\left(1-u_y{ }^2\right)\left(\mathrm{d} a_y / \mathrm{d} t\right)-u_x u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right)-u_y\left(\mathrm{~d} a_x / \mathrm{d} y-\mathrm{d} a_y / \mathrm{d} x\right) \\ \mathrm{d} \gamma / \mathrm{d} t=u_x\left(\mathrm{~d} a_x / \mathrm{d} t\right)+u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right) \\ \gamma=\left(1-u_x^2-u_y^2-u_z^2\right)^{-1 / 2} \end{array}\right. (9) 式中,ux,uy,uz为高能电子在坐标轴上的速度分量的大小;ax和ay为归一化矢势分量的大小。根据电动力学的知识,电子在加速运动时发射电磁辐射,由下式控制:
\frac{\mathrm{d} P(t)}{\mathrm{d} \boldsymbol{{\mathit{\Omega}}}}=\left|\frac{|\boldsymbol{n} \times[(\boldsymbol{n}-\boldsymbol{u}) \times(\mathrm{d} \boldsymbol{u} / \mathrm{d} t)]|^2}{(1-\boldsymbol{n} \cdot \boldsymbol{u})^6}\right|_{t'} (10) 式中,\frac{\mathrm{d} P(t)}{\mathrm{d} {\mathit{\Omega}}} \text { 是被 } \frac{e^2 \omega_0^2}{4 {\rm{ \mathsf{π} }} c}归一化的单位立体角辐射功率; n为辐射方向; du/dt为电子的加速度。电子辐射方向在笛卡尔坐标系中可以表示为:
\boldsymbol{n}=\sin \theta \cos \phi \cdot \boldsymbol{x}+\sin \theta \sin \phi \cdot \boldsymbol{y}+\cos \theta \cdot \boldsymbol{z} (11) 式中,θ和ϕ分别表示与激光运动方向的夹角和垂直于碰撞方向的平面上的偏转方位角。此外,Δt为发生碰撞时刻t与观察到碰撞现象时刻t'之间的时间间隔。
\Delta t=t-t^{\prime}=S_0-\boldsymbol{n} \cdot \boldsymbol{r} (12) 式中,S0表示观测点距离碰撞中心的距离,r为电子位置矢量。
通过上述方程能够得到脉冲激光和高能电子作用的过程中能量和功率随观测角的变化情况。
2. 数值模拟结果
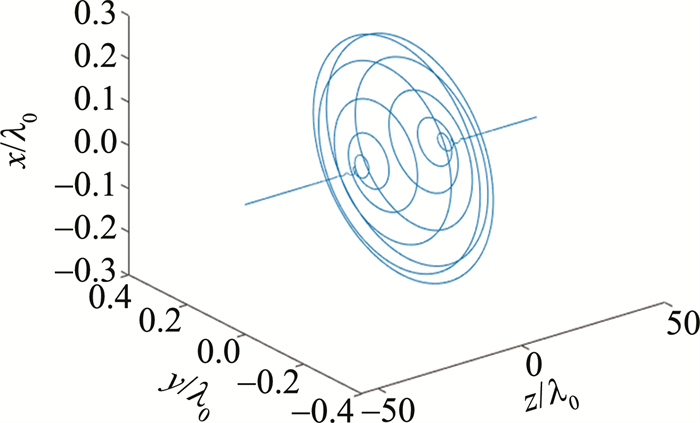
通过MATLAB软件计算来对高能电子与强激光场脉冲对撞过程中的电子轨迹进行迭代运算和模拟,得到电子在空间坐标系下的运动状态图,如图 2所示。对于位于激光传播轴上的初始静止电子,图 2是圆偏振高斯脉冲作用于电子时,电子的运动轨迹曲线,发现在对撞过程中, 电子绕激光传播轴的运动轨迹呈现螺旋状,且沿着+z轴方向传播,电子的能量总体增益先增加,然后下降,其激光脉宽L=3λ0,束腰半径b0=3λ0,初始相位φ0=0°。
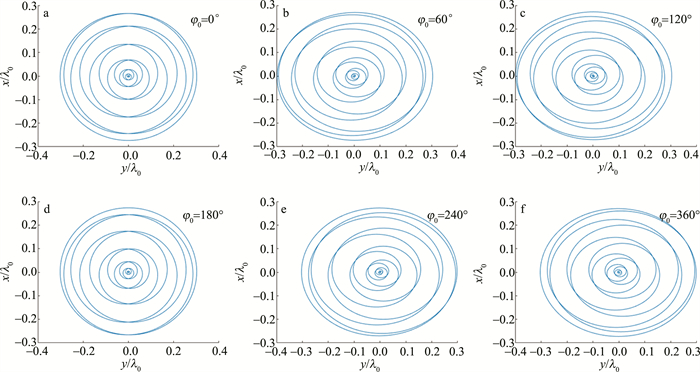
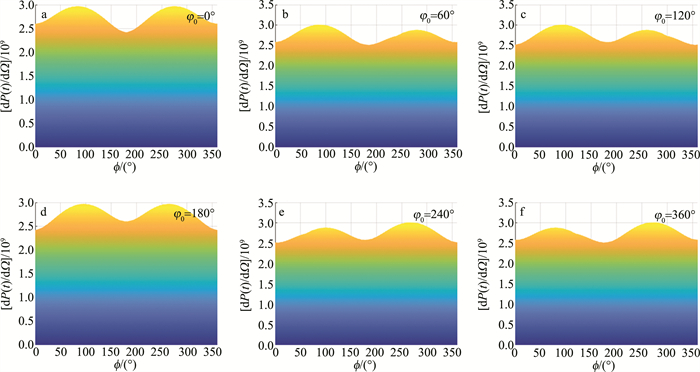
固定L和b0均取为3λ0,用不同初始相位的椭圆偏振激光器驱动,对电子的运动轨迹进行数值模拟,将所得图像沿x/λ0和y/λ0展开,得到的电子运动轨迹,如图 3所示。从图 3可以看出,高能电子的运动轨迹为1维平面对称,高能电子的运动轨迹与激光脉冲的初始相位有着较为紧密的联系。图 3中激光初始相位φ0为0°和180°时,电子的运动轨迹沿平面y=0呈直线-螺旋-直线对称图像。而图 3中其它初始相位对应电子运动轨迹不关于平面y=0对称。继续保持L和b0取值不变,利用MATLAB进行数据计算与图像处理,得到不同初始相位下激光脉冲对高能电子的辐射图像,将所得到的图像沿θ和dP(t)/dΩ展开,如图 4所示。通过图像结合数据分析可知,当激光初始相位φ0=0°时,电子最大辐射功率双峰图像关于ϕ=179.5°对称,且双峰辐射功率最大值均约为2.96970×109,图 4中激光初始相位φ0=180°时,电子最大辐射功率双峰图像也呈现出双峰对称性;而当激光初始相位φ0为60°,120°,240°,300°时,双峰图像呈现出不对称性。这是由于在改变了与高能电子对撞的激光脉冲初始相位之后,电子的运动轨迹随之发生变化,导致单位立体角内的辐射功率发生改变。
从图 4还可以看出,电子最大辐射功率图随着激光初始相位的改变,呈循环态势。在初始相位φ0大于0°而小于180°期间,左峰峰值高于右峰峰值; 在φ0大于180°而小于360°期间,右峰峰值高于左峰峰值。
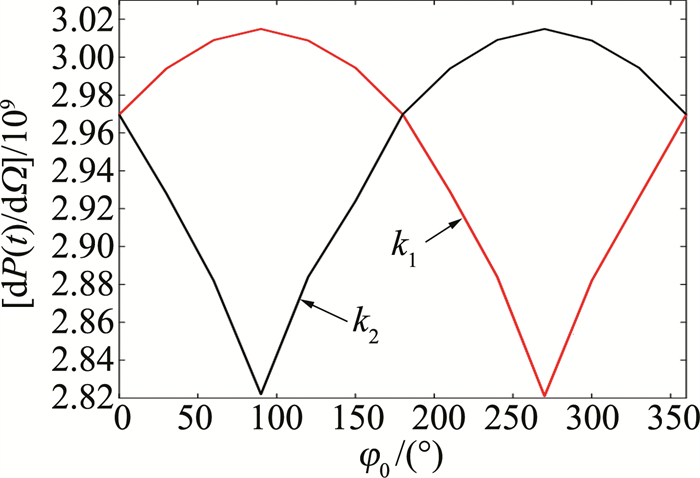
为了进一步探究电子辐射分布中两峰值数值随着激光初始相位的变化,令初始相位φ0从0°变化到360°,每隔30°记录一次数据,对不同初始相位所对应的最大辐射功率图像进行仿真,计算收集图像左右双峰的极大值,并对双峰的极大值进行比较,设最大辐射功率图像左峰极大值为k1,右峰极大值为k2,得到如图 5所示的图像。从图 5可以观察到,随着初始相位的不断增加,k1值也在增加,并在φ0=90°时增加至最大值,约为3.01490×109,而后逐渐下降,在φ0=270°时取得最小值,然后继续增长,在φ0=360°时取得与0°时相同的数值,完成了一次循环。观察k1和k2数值随初始相位变化图像,不难发现其变化趋势也具有一定的对称性,且k1和k2两线交汇处表示此刻最大辐射功率图像呈现出对称型双峰。
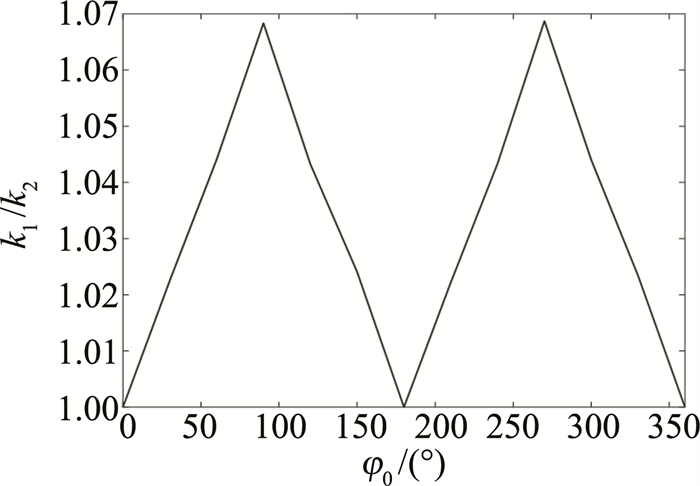
为更直观地说明图像是否对称,作者将图 5中得到的k1与k2的数值相除,得到图 6所示的图像。图 6进一步说明了当激光初始相位φ0为0°,180°和360°时,k1/k2的比值约为1,即双峰数值近乎相等,电子最大辐射功率图像呈现出对称型双峰,而在其它初始相位下呈现出非对称型双峰。
3. 结论
根据Lorentz方程与电子能量方程构造高能电子与强激光场的对撞模型,利用控制变量法,改变超短超强椭圆激光脉冲初始相位。利用MATLAB软件进行数值模拟,探究超短超强椭圆激光脉冲驱动高能电子辐射的影响,结果表明,当激光脉冲撞击电子时,电子产生辐射,且辐射功率呈现双峰形; 高能电子的辐射功率图像在激光初始相位φ0为0°,180°和360°时表现为对称型双峰, 而在其它相位下辐射功率图像呈现出非对称形双峰。此发现为超短超强椭圆偏振激光的初始相位3维反探测研究提供了一定的基础,即可以通过高能电子辐射功率的空间分布来探测出激光脉冲的初始相位。
-
-
[1] VAIS O E, BYCHENKOV V Y. Complementary diagnostics of high-intensity femtosecond laser pulses via vacuum acceleration of protons and electrons[J]. Plasma Physics and Controlled Fusion, 2021, 63(1): 014002. DOI: 10.1088/1361-6587/abc92a
[2] KOZÁK M. All-optical scheme for generation of isolated attosecond electron pulses[J]. Physical Review Letters, 2019, 123(20): 203202. DOI: 10.1103/PhysRevLett.123.203202
[3] COUSENS S, REVILLE B, DROMEY B, et al. Temporal structure of attosecond pulses from laser-driven coherent synchrotron emission[J]. Physical Review Letters, 2016, 116(8): 083901. DOI: 10.1103/PhysRevLett.116.083901
[4] VENKAT P, HOLKUNDKAR A R. Higher harmonics and attosecond pulse generation by laser induced Thomson scattering in atomic clusters[J]. Physical Review Accelerators and Beams, 2019, 22(8): 084401. DOI: 10.1103/PhysRevAccelBeams.22.084401
[5] KOZÁK M, SCHÖNENBERGER N, HOMMELHOFF P. Ponderomotive generation and detection of attosecond free-electron pulse trains[J]. Physical Review Letters, 2018, 120(10): 103203. DOI: 10.1103/PhysRevLett.120.103203
[6] HACK S, VARRÓ S, CZIRJÁK A. Carrier-envelope phase controlled isolated attosecond pulses in the nm wavelength range, based on coherent nonlinear Thomson-backscattering[J]. New Journal of Phy-sics, 2018, 20(7): 073043. DOI: 10.1088/1367-2630/aad2aa
[7] FRYDRYCH S, VORBERGER J, HARTLEY N J, et al. Demonstration of X-ray Thomson scattering as diagnostics for miscibility in warm dense matter[J]. Nature Communications, 2020, 11(1): 1-7. DOI: 10.1038/s41467-019-13993-7
[8] KARBSTEIN F, MOSMAN E A. X-ray photon scattering at a focused high-intensity laser pulse[J]. Physical Review D, 2019, 100(3): 033002. DOI: 10.1103/PhysRevD.100.033002
[9] RYKOVANOV S G, GEDDES C G R, SCHROEDER C B, et al. Controlling the spectral shape of nonlinear Thomson scattering with proper laser chirping[J]. Physical Review Accelerators and Beams, 2016, 19(3): 30701. DOI: 10.1103/PhysRevAccelBeams.19.030701
[10] CHI Z, DU Y, HUANG W, et al. Linearly polarized X-ray fluore-scence computed tomography based on a Thomson scattering light source: A Monte Carlo study[J]. Journal of Synchrotron Radiation, 2020, 27(3): 737-745. DOI: 10.1107/S1600577520003574
[11] TAIRA Y, HAYAKAWA T, KATOH M. Gamma-ray vortices from nonlinear inverse Thomson scattering of circularly polarized light[J]. Scientific Reports, 2017, 7(1): 1-9. DOI: 10.1038/s41598-016-0028-x
[12] WANG Y, WANG C, ZHOU Q, et al. Nonlinear Thomson scattering from a tightly focused circularly polarized laser with varied incident-pulse durations[J]. Laser Physics, 2021, 31(1): 015301. DOI: 10.1088/1555-6611/abd3f7
[13] VAIS O E, BYCHENKOV V Y. Nonlinear Thomson scattering of a tightly focused relativistically intense laser pulse by an ensemble of particles[J]. Quantum Electronics, 2020, 50(10): 922. DOI: 10.1070/QEL17344
[14] YAN W, FRUHLING C, GOLOVIN G, et al. High-order multiphoton Thomson scattering[J]. Nature Photonics, 2017, 11(8): 514-520. DOI: 10.1038/nphoton.2017.100
[15] WANG Y, ZHOU Q, ZHUANG J, et al. Vortex and symmetric radiation character of nonlinear Thomson scattering in Laguerre-Gaussian circularly polarized laser pulses[J]. Optics Express, 2021, 29(14): 22636-22647. DOI: 10.1364/OE.426529
[16] LI K, LI L, SHU Q, et al. Spatial characteristics of motion and emission from electron driven by linearly polarized tightly focused laser pulses[J/OL]. (2019-02-26)[2021-12-26]. https://www.sciencedirect.com/science/article/pii/S0030402619302712.
[17] WANG Y, WANG C, LI K, et al. Spatial radiation features of Thomson scattering from electron in circularly polarized tightly focused laser beams[J]. Laser Physics Letters, 2021, 18(1): 015303. DOI: 10.1088/1612-202X/abd170
[18] 严以律, 周希, 任山令, 等. 电子初始位置对高能电子空间辐射的影响[J]. 激光技术, 2022, 46(4): 556-560. DOI: 10.7510/jgjs.issn.1001-3806.2022.04.019 YAN Y L, ZHOU X, REN Sh L, et al. Effect of initial position of electron on space radiation of high energy electron[J]. Laser Technology, 2022, 46(4): 556-560(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2022.04.019
[19] YU P, LIN H, GU Z, et al. Analysis of the beam waist on spatial emission characteristics from an electron driven by intense linearly polarized laser pulses[J]. Laser Physics, 2020, 30(4): 045301. DOI: 10.1088/1555-6611/ab74d4
[20] WU Y, LIU Y, LIU D, et al. Effect of circularly polarized laser pulse beam waist radius on the dynamic and radiation characteristics of collided electrons[J]. Laser Physics, 2020, 30(11): 115301. DOI: 10.1088/1555-6611/abb6e5
[21] SHI Y, WANG J, WU B, et al. Nonlinear Thomson scattering of a relativistic elliptically polarized laser with varied incident pulse widths[J]. Laser Physics, 2021, 31(10): 105401. DOI: 10.1088/1555-6611/ac250e



 下载:
下载: