Power grid insulator identification method based on airborne laser point cloud
-
摘要: 为了解决无人机机载激光雷达采集到的点云数据存在密度高但分布不均匀的现象, 以及绝缘子表面纹理信息不全等问题, 提出了一种基于机载激光点云的电网绝缘子识别方法。首先分析杆塔中不同部位的强度值直方图, 用强度值滤波剔除大部分的杆身点云; 然后采用主成分分析法计算局部点云特征值, 根据特征值构建的局部熵函数和空间分布特性删除冗余的平坦区域点云, 并通过栅格修补的方法避免出现点云空洞; 最后针对传统采样一致性初始配准(SAC-IA)算法精度低和速度慢的问题, 通过增加采样点对的距离约束关系和自适应调整参数改进SAC-IA算法完成绝缘子的位姿估计。结果表明, 该方法能正确高效地识别杆塔中的绝缘子, 运行时间大幅减少, 提取正确率达到95.16%。该研究在无人机自主巡检航线规划中具有良好的应用价值。Abstract: To solve the problems of high density but uneven distribution of point cloud data collected by ummanned aerial vehicle (UAV) airborne lidar and incomplete information on the surface texture of insulators, a power grid insulator identification method based on airborne laser point cloud was proposed. Firstly, the histogram of the intensity value of different parts of the tower was analyzed, and the intensity value filter was used to remove most of the tower body point cloud; the principal component analysis method was then used to calculate the local point cloud eigenvalues. The local entropy function and spatial distribution characteristics based on the eigenvalues delete redundant flat area point clouds was built. Grid patching was used to avoid point cloud holes; finally, to solve the problem of low accuracy and slow speed of the traditional sample consensus initial alignment (SAC-IA) algorithm, the SAC-IA algorithm was improved to complete the pose estimation of the insulator by increasing the distance constraint relationship of the sampling point pair and adaptive adjustment parameters. The experimental results show that the insulators in the tower can be identified accurately and efficiently by using this method. And the running time is greatly reduced, and the extraction accuracy rate reaches 95.16%, which has good application value in UAV autonomous inspection route planning.
-
引言
自20世纪90年代以来，啁啾脉冲放大技术的出现见证了激光技术的蓬勃发展。如今超短超强激光脉冲的闪亮时间早已达到飞秒[1-2]甚至阿秒[3-6]量级。超短超强激光脉冲的发展在X射线[7-9]、医疗行业[10]和天体物理[11]等研究领域也有着重要的贡献。
在非线性汤姆逊散射[12-14]中，入射激光脉冲的各种参数会影响电子的运动轨迹和辐射特性。例如WANG等人[15]研究了不同脉冲宽度下紧密聚焦圆偏振激光脉冲的非线性汤姆逊散射。LI[16]和WANG[17]等人研究了不同激光强度下圆极化聚焦照射电子的运动和空间辐射特性。YAN等人[18]研究了电子初始位置对高能电子辐射的影响。YU[19]和WU[20]等人研究了不同束腰半径的激光脉冲对电子的影响。而SHI等人[21]发现了在椭圆偏振激光脉冲中，随着脉冲宽度的增加，电子的空间辐射分布有更多的局部极大值集且每组有4个局部极大值。本文作者也是在椭圆偏振激光脉冲的基础上进行研究，但与SHI等人不同的是，本文中研究了超短超强椭圆激光脉冲的初始相位对高能电子运动轨迹和辐射功率空间分布的影响。
作者探讨了高能电子在激光场中的运动，应用Lorentz方程与电子能量方程建立强激光场与单个高能电子的对撞模型，对不同初始相位的椭圆偏振脉冲激光场对撞高能电子所产生的空间辐射功率图像进行模拟，详细讨论了椭圆偏振激光脉冲的初始相位对于高能电子产生辐射功率空间分布的影响，能够通过高能电子辐射功率的空间分布探测出超短超强椭圆偏振激光脉冲的初始相位。
1. 单电子对撞辐射模型
紧聚焦高斯脉冲激光电场的归一化矢势a(η)可以表示为：
\boldsymbol{a}(\eta)=a(\cos \varphi \cdot \boldsymbol{x}+\delta \sin \varphi \cdot \boldsymbol{y}) (1) a=\frac{b_0}{b} a_0 \exp \left(-\frac{\eta^2}{L^2}-\frac{\rho^2}{b^2}\right) (2) 式中，a0=0.85×10-9λ0\sqrt{I}是通过mc2/e进行归一化的激光振幅，其中m和e分别为电子静止时的质量和电量，c是光速，I和λ0为激光强度峰值和激光波长；η=z-t，z和t表示电子在z轴的坐标和观察点的时间；L是激光的脉宽；δ为偏振参量，椭圆偏振下0 < δ < 1；b=b0(1+z2/zR2)1/2为脉冲传播到z轴时的束腰半径；zR=b02/2为瑞利长度；b0是b的最小值；ρ2=x2+y2代表与传播方向的垂直距离，高斯脉冲形状是分别由横向参数exp(-ρ2/b2)和纵向参数exp(-η2/L2)所决定。定义脉冲相位为：
\varphi=c_0 \eta^2+\eta+\varphi_R-\varphi_{\mathrm{G}}+\varphi_0 (3) 式中，φ0是激光脉冲的初始相位；c0为激光啁啾参数；φG=z/zR为古伊相位；φR=ρ2/2R(z)与波前曲率有关，R(z)=z(1+1/φG2)为波前曲率半径。在上述定义中，k0-1和ω0-1已将空间坐标和时间坐标归一化，其中k0和ω0为激光的波数和频率。在库仑定律▽·a=0下，矢场纵向分量为：
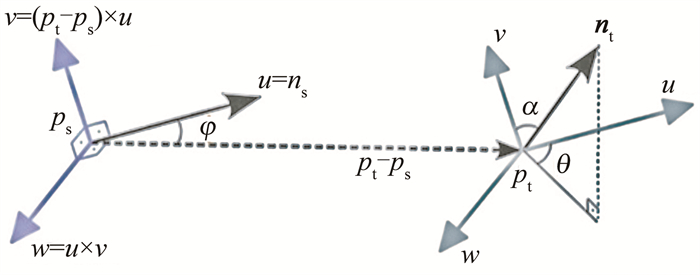
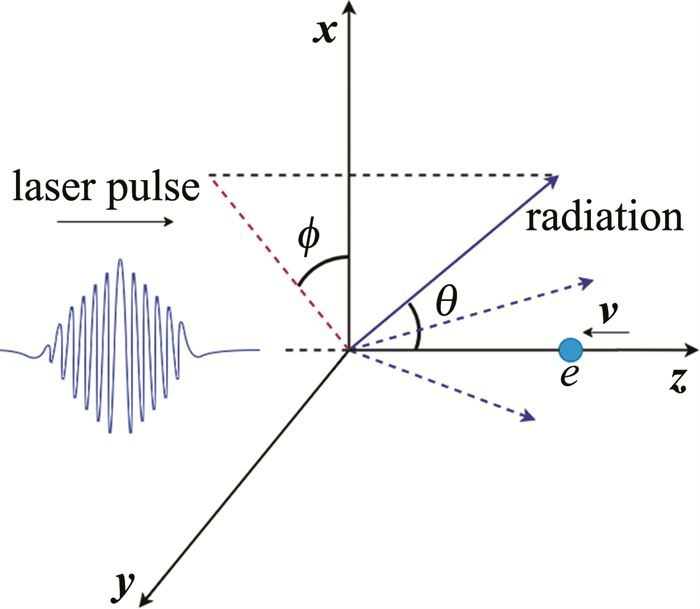
\boldsymbol{a}_z=\frac{2 a[-x \cos (\varphi+\theta)+\delta y \sin (\varphi+\theta)] \boldsymbol{z}}{b_0 b} (4) 式中，θ=π-arctan(z/zR)。椭圆偏振激光脉冲与高能电子相互作用的示意图如图 1所示。
![图 1 激光脉冲与电子相互作用示意图]()
图 1 激光脉冲与电子相互作用示意图Figure 1. Schematic diagram of interaction between laser pulse and electron设电子沿着-z轴方向移动，激光脉冲沿z轴正方向移动。在真空激光和单电子理论中，激光场中电场强度E=-da/dt，给出真空中单电子与激光发生碰撞运动的基本方程：
\nabla^2 \boldsymbol{a}+\mathrm{d} \boldsymbol{a} / \mathrm{d} \boldsymbol{u}=0 (5) \mathrm{d}(\boldsymbol{p}-\boldsymbol{a}) / \mathrm{d} t=-\nabla \gamma (6) \mathrm{d} \gamma / \mathrm{d} t=\boldsymbol{u} \cdot(\mathrm{d} \boldsymbol{a} / \mathrm{d} t) (7) 式中，u为电子的速度；p=γu为电子动量; γ=(1-u2)-1/2为电子能量。考虑到：
\nabla \gamma=(\boldsymbol{u} \cdot \nabla) \boldsymbol{p}+\boldsymbol{u} \times(\nabla \times \boldsymbol{a}) (8) 由于矢量势垂直于激光传播方向，电子的速度可以分解为正交分量：
\left\{\begin{array}{l} \gamma\left(\mathrm{d} u_x / \mathrm{d} t\right)=\left(1-u_x{ }^2\right)\left(\mathrm{d} a_x / \mathrm{d} t\right)-u_x u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right)+u_y\left(\mathrm{~d} a_x / \mathrm{d} y-\mathrm{d} a_y / \mathrm{d} x\right) \\ \gamma\left(\mathrm{d} u_y / \mathrm{d} t\right)=\left(1-u_y{ }^2\right)\left(\mathrm{d} a_y / \mathrm{d} t\right)-u_x u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right)-u_y\left(\mathrm{~d} a_x / \mathrm{d} y-\mathrm{d} a_y / \mathrm{d} x\right) \\ \mathrm{d} \gamma / \mathrm{d} t=u_x\left(\mathrm{~d} a_x / \mathrm{d} t\right)+u_y\left(\mathrm{~d} a_y / \mathrm{d} t\right) \\ \gamma=\left(1-u_x^2-u_y^2-u_z^2\right)^{-1 / 2} \end{array}\right. (9) 式中，ux，uy，uz为高能电子在坐标轴上的速度分量的大小；ax和ay为归一化矢势分量的大小。根据电动力学的知识，电子在加速运动时发射电磁辐射，由下式控制：
\frac{\mathrm{d} P(t)}{\mathrm{d} \boldsymbol{{\mathit{\Omega}}}}=\left|\frac{|\boldsymbol{n} \times[(\boldsymbol{n}-\boldsymbol{u}) \times(\mathrm{d} \boldsymbol{u} / \mathrm{d} t)]|^2}{(1-\boldsymbol{n} \cdot \boldsymbol{u})^6}\right|_{t'} (10) 式中，\frac{\mathrm{d} P(t)}{\mathrm{d} {\mathit{\Omega}}} \text { 是被 } \frac{e^2 \omega_0^2}{4 {\rm{ \mathsf{π} }} c}归一化的单位立体角辐射功率; n为辐射方向; du/dt为电子的加速度。电子辐射方向在笛卡尔坐标系中可以表示为：
\boldsymbol{n}=\sin \theta \cos \phi \cdot \boldsymbol{x}+\sin \theta \sin \phi \cdot \boldsymbol{y}+\cos \theta \cdot \boldsymbol{z} (11) 式中，θ和ϕ分别表示与激光运动方向的夹角和垂直于碰撞方向的平面上的偏转方位角。此外，Δt为发生碰撞时刻t与观察到碰撞现象时刻t'之间的时间间隔。
\Delta t=t-t^{\prime}=S_0-\boldsymbol{n} \cdot \boldsymbol{r} (12) 式中，S0表示观测点距离碰撞中心的距离，r为电子位置矢量。
通过上述方程能够得到脉冲激光和高能电子作用的过程中能量和功率随观测角的变化情况。
2. 数值模拟结果
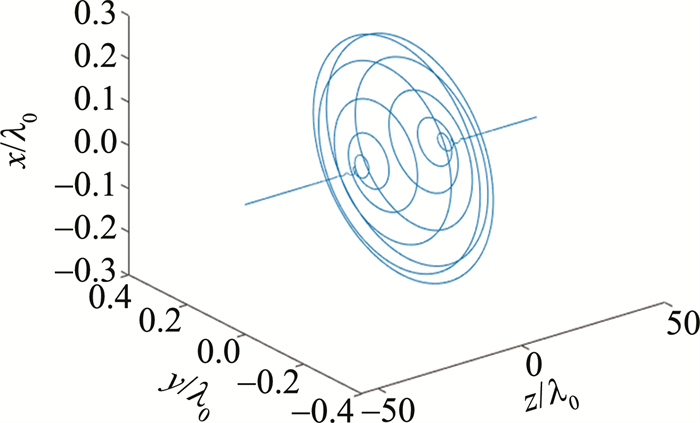
通过MATLAB软件计算来对高能电子与强激光场脉冲对撞过程中的电子轨迹进行迭代运算和模拟，得到电子在空间坐标系下的运动状态图，如图 2所示。对于位于激光传播轴上的初始静止电子，图 2是圆偏振高斯脉冲作用于电子时，电子的运动轨迹曲线，发现在对撞过程中, 电子绕激光传播轴的运动轨迹呈现螺旋状，且沿着+z轴方向传播，电子的能量总体增益先增加，然后下降，其激光脉宽L=3λ0，束腰半径b0=3λ0，初始相位φ0=0°。
![图 2 高能电子与激光场对撞过程中电子运动轨迹图]()
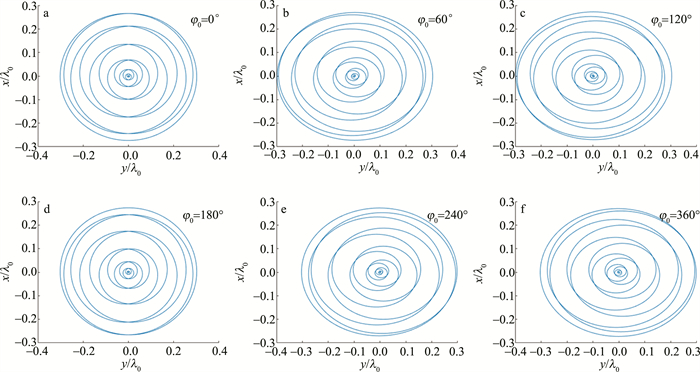
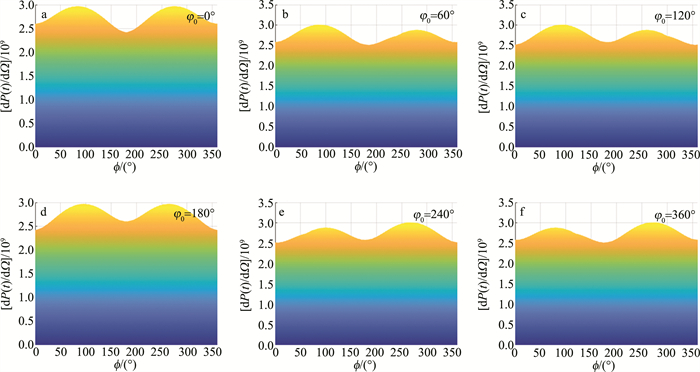
图 2 高能电子与激光场对撞过程中电子运动轨迹图Figure 2. Electron trajectory during the collision between high energy electron and laser field固定L和b0均取为3λ0，用不同初始相位的椭圆偏振激光器驱动，对电子的运动轨迹进行数值模拟，将所得图像沿x/λ0和y/λ0展开，得到的电子运动轨迹，如图 3所示。从图 3可以看出，高能电子的运动轨迹为1维平面对称，高能电子的运动轨迹与激光脉冲的初始相位有着较为紧密的联系。图 3中激光初始相位φ0为0°和180°时，电子的运动轨迹沿平面y=0呈直线-螺旋-直线对称图像。而图 3中其它初始相位对应电子运动轨迹不关于平面y=0对称。继续保持L和b0取值不变，利用MATLAB进行数据计算与图像处理，得到不同初始相位下激光脉冲对高能电子的辐射图像，将所得到的图像沿θ和dP(t)/dΩ展开，如图 4所示。通过图像结合数据分析可知，当激光初始相位φ0=0°时，电子最大辐射功率双峰图像关于ϕ=179.5°对称，且双峰辐射功率最大值均约为2.96970×109，图 4中激光初始相位φ0=180°时，电子最大辐射功率双峰图像也呈现出双峰对称性；而当激光初始相位φ0为60°，120°，240°，300°时，双峰图像呈现出不对称性。这是由于在改变了与高能电子对撞的激光脉冲初始相位之后，电子的运动轨迹随之发生变化，导致单位立体角内的辐射功率发生改变。
![图 3 不同初始相位圆偏振激光器驱动所得电子运动轨迹]()
图 3 不同初始相位圆偏振激光器驱动所得电子运动轨迹Figure 3. Electron trajectories driven by circularly polarized lasers with different initial phases从图 4还可以看出，电子最大辐射功率图随着激光初始相位的改变，呈循环态势。在初始相位φ0大于0°而小于180°期间，左峰峰值高于右峰峰值; 在φ0大于180°而小于360°期间，右峰峰值高于左峰峰值。
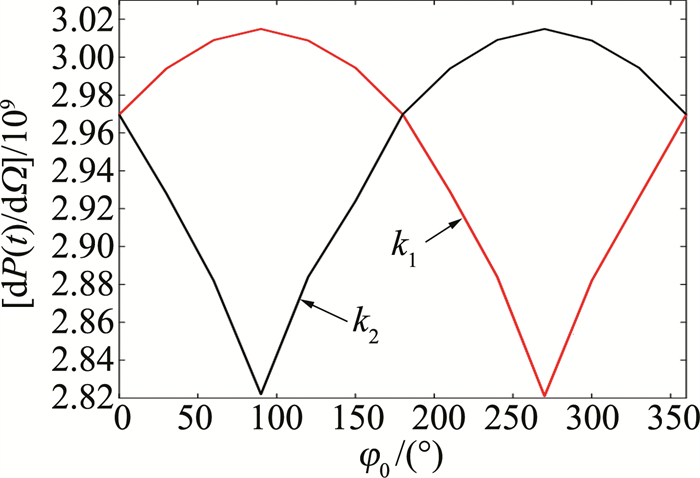
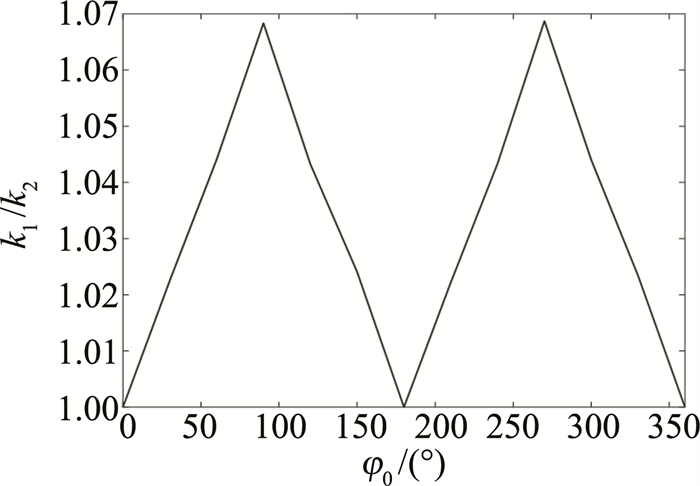
为了进一步探究电子辐射分布中两峰值数值随着激光初始相位的变化，令初始相位φ0从0°变化到360°，每隔30°记录一次数据，对不同初始相位所对应的最大辐射功率图像进行仿真，计算收集图像左右双峰的极大值，并对双峰的极大值进行比较，设最大辐射功率图像左峰极大值为k1，右峰极大值为k2，得到如图 5所示的图像。从图 5可以观察到，随着初始相位的不断增加，k1值也在增加，并在φ0=90°时增加至最大值，约为3.01490×109，而后逐渐下降，在φ0=270°时取得最小值，然后继续增长，在φ0=360°时取得与0°时相同的数值，完成了一次循环。观察k1和k2数值随初始相位变化图像，不难发现其变化趋势也具有一定的对称性，且k1和k2两线交汇处表示此刻最大辐射功率图像呈现出对称型双峰。
![图 5 双峰极大值k1和k2随初始相位的数值变化]()
图 5 双峰极大值k1和k2随初始相位的数值变化Figure 5. Numerical variation of bimodal maximum k1 and k2 with initial phase为更直观地说明图像是否对称，作者将图 5中得到的k1与k2的数值相除，得到图 6所示的图像。图 6进一步说明了当激光初始相位φ0为0°，180°和360°时，k1/k2的比值约为1，即双峰数值近乎相等，电子最大辐射功率图像呈现出对称型双峰，而在其它初始相位下呈现出非对称型双峰。
![图 6 最大辐射功率图像双峰极大值数值之比]()
图 6 最大辐射功率图像双峰极大值数值之比Figure 6. Ratio of the maximum radiation power to the bimodal maximum of the image3. 结论
根据Lorentz方程与电子能量方程构造高能电子与强激光场的对撞模型，利用控制变量法，改变超短超强椭圆激光脉冲初始相位。利用MATLAB软件进行数值模拟，探究超短超强椭圆激光脉冲驱动高能电子辐射的影响，结果表明，当激光脉冲撞击电子时，电子产生辐射，且辐射功率呈现双峰形; 高能电子的辐射功率图像在激光初始相位φ0为0°，180°和360°时表现为对称型双峰, 而在其它相位下辐射功率图像呈现出非对称形双峰。此发现为超短超强椭圆偏振激光的初始相位3维反探测研究提供了一定的基础，即可以通过高能电子辐射功率的空间分布来探测出激光脉冲的初始相位。
-
![]()
图 2 错误配对点的选取示例
a—绝缘子随机采样点b—杆塔对应采样点
Figure 2. Example of picking incorrect matching points
a—random sampling point of insulator b—sampling point corresponding to the tower
![]()
图 3 杆塔中不同区域的强度值直方图
Figure 3. Istogram of the intensity value of different areas in the tower
![]()
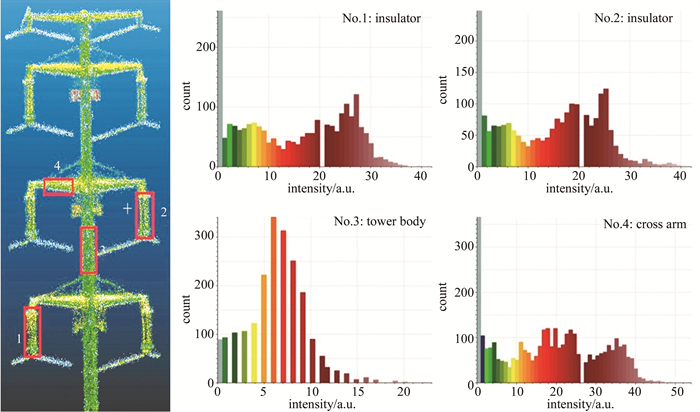
图 4 杆塔和绝缘子模板的预处理
a—杆塔原始数据b—杆塔强度值滤波c—杆塔局部熵精简d—模板原始数据e—模板强度值滤波f—模板局部熵精简
Figure 4. Pretreatment of tower and insulator template
a—raw data of tower b—intensity value filtering for tower c—local entropy simplifying for tower d—raw data of template e—intensity value filtering for template f—local entropy simplifying for template
表 1 杆塔与绝缘子模板的点云数
Table 1 Point cloud number of tower and insulator template
data source raw data intensity value filtering local entropysimplifying tower 170351 86123 26413 insulator template 2983 1774 1126 
下载: 导出CSV
表 2 改进SAC-IA算法对绝缘子定位
Table 2 Improved SAC-IA algorithm for insulator location
the first time the second time the third time the fourth time the fifth time the sixth time 3-D center coordinates/m x 1134.98 1135.02 1134.96 1135.92 1135.87 1135.41 y 151.98 151.949 151.899 157.342 157.386 157.346 z 293.89 289.9 151.899 289.783 293.911 285.85 running time/s 9.34 8.97 8.28 7.70 7.99 8.72 effective iterations 2250 2297 2216 2330 1982 1907
下载: 导出CSV
表 3 4种方法的结果分析
Table 3 Analysis of the results of the four methods
algorithm number of correctly positioned insulators in a single tower accuracy/% average time to locate a single insulator/s 0# 1# 2# 3# 4# 5# 6# A 10 6 5 3 4 3 0 30.11 31.62 B 3 4 4 6 6 4 4 52.69 15.95 C 0 0 5 8 6 5 7 67.20 11.14 ours 0 0 0 0 2 5 24 95.16 7.82
下载: 导出CSV
-
[1] 刘澈, 姜勇, 姚森敬, 等. 基于多传感器信息融合的绝缘子串自动识别方法[J]. 机械设计与制造, 2019(4): 220-224. DOI: 10.3969/j.issn.1001-3997.2019.04.055 LIU Ch, JIANG Y, YAO S J, et al. The method to automatic recognition of insulator based on multi-sensor information fusion[J]. Machinery Design & Manufacture, 2019(4): 220-224(in Chinese). DOI: 10.3969/j.issn.1001-3997.2019.04.055
[2] MATIKAINEN L, LEHTOMÄKI M, AHOKAS E, et al. Remote sensing methods for power line corridor surveys[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 119: 10-31. DOI: 10.1016/j.isprsjprs.2016.04.011
[3] GUAN H, SUN X, SU Y, et al. UAV-lidar aids automatic intelligent powerline inspection[J]. International Journal of Electrical Power & Energy Systems, 2021, 130: 106987.
[4] 李靖, 钱建国, 王伟玺, 等. 基于机载激光点云的电力线自动提取方法[J]. 激光技术, 2021, 45(3): 362-366. DOI: 10.7510/jgjs.issn.1001-3806.2021.03.017 LI J, QIAN J G, WANG W X, et al. Power line automatic extraction method based on airborne laser point cloud[J]. Laser Technology, 2021, 45(3): 362-366(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2021.03.017
[5] LIN T, LIU X. An intelligent recognition system for insulator string defects based on dimension correction and optimized faster R-CNN[J]. Electrical Engineering, 2021, 103(1): 541-549. DOI: 10.1007/s00202-020-01099-z
[6] 陈亮. 基于高密度机载激光点云的输电线路杆塔信息提取[D]. 锦州: 辽宁工程技术大学, 2016: 37-54. CHEN L. Information extraction of transmission line tower based on high density airborne laser point cloud[D]. Jinzhou: Liaoning Technical University, 2016: 37-54(in Chinese).
[7] 王平华, 习晓环, 王成, 等. 机载激光雷达数据中电力线的快速提取[J]. 测绘科学, 2017, 42(2): 154-158. https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201702029.htm WANG P H, XI X H, WANG Ch, et al. Study on power line fast extraction based on airborne LiDAR data[J]. Science of Surveying and Mapping, 2017, 42(2): 154-158(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201702029.htm
[8] 徐梁刚, 虢韬, 吴绍华, 等. 基于点云数据特征的电力线快速提取和重建[J]. 激光技术, 2020, 44(2): 244-249. DOI: 10.7510/jgjs.issn.1001-3806.2020.02.019 XU L G, GUO T, WU Sh H, et al. Fast extraction and reconstruction of power line based on point cloud data features[J]. Laser Technology, 2020, 44(2): 244-249(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2020.02.019
[9] ORTEGA S, TRUJILLO A, SANTANA J M, et al. Characterization and modeling of power line corridor elements from LiDAR point clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 152: 24-33. DOI: 10.1016/j.isprsjprs.2019.03.021
[10] ZHANG R, YANG B, XIAO W, et al. Automatic extraction of high-voltage power transmission objects from UAV lidar point clouds[J]. Remote Sensing, 2019, 11(22): 2600. DOI: 10.3390/rs11222600
[11] 杨诗语. 基于点云的杆塔绝缘子分类方法研究[D]. 保定: 华北电力大学, 2016: 54-67. YANG Sh Y. Research on classification method of insulators based on point cloud[D]. Baoding: North China Electric Power University, 2020: 54-67(in Chinese).
[12] ARASTOUNIA M, LICHTI D D. Automatic extraction of insulators from 3D LiDAR data of an electrical substation[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, Ⅱ-5/W2: 19-24.
[13] SUN Y, CHEN X, JIAN X, et al. Identification and localization method of the insulator based on three-dimensional point cloud modeling[C]//2019 Chinese Control Conference (CCC). New York, USA: IEEE, 2019: 7051-7056.
[14] 刘经南, 张小红. 利用激光强度信息分类激光扫描测高数据[J]. 武汉大学学报(信息科学版), 2005, 30(3): 189-193. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH200503000.htm LIU J N, ZHANG X H. Classification of laser scanning altimetry data using laser intensity[J]. Geomatics and Information Science of Wuhan University, 2005, 30(3): 189-193. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH200503000.htm
[15] 刘国栋, 刘佳, 刘浪. 一种基于机载LiDAR数据的山区道路提取方法[J]. 激光技术, 2022, 46(4): 466-473. DOI: 10.7510/jgjs.issn.1001-3806.2022.04.005 LIU G D, LIU J, LIU L. A mountain road extraction method based on airborne LiDAR data[J]. Laser Technology, 2022, 46(4): 466-473(in Chinese). DOI: 10.7510/jgjs.issn.1001-3806.2022.04.005
[16] 王明军, 易芳, 李乐, 等. 自适应局部邻域特征点提取和匹配的点云配准[J]. 红外与激光工程, 2021, 51(5): 421-430. https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ202205048.htm WANG M J, YI F, LI L, et al. Local neighborhood feature point extraction and matching for point cloud alignment[J]. Infrared and Laser Engineering, 2021, 51(5): 421-430(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ202205048.htm
[17] 林松, 田林亚, 毕继鑫, 等. 基于最优邻域局部熵的点云精简算法[J]. 测绘工程, 2021, 30(5): 12-17. https://www.cnki.com.cn/Article/CJFDTOTAL-CHGC202105003.htm LIN S, TIAN L Y, BI J X, et al. Point cloud simplification algorithm based on local entropy of optimal neighborhood[J]. Engineering of Surveying and Mapping, 2021, 30(5): 12-17(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CHGC202105003.htm
[18] XUAN W, HUA X, CHEN X, et al. A new progressive simplification method for point cloud using local entropy of normal angle[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(4): 581-589.
[19] RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration[C]//2009 IEEE International Confe-rence on Robotics and Automation. New York, USA: IEEE, 2009: 3212-3217.
[20] DING Q, HE J. The detection of non-cooperative targets in space by using 3D point cloud[C]//2019 5th International Conference on Control, Automation and Robotics (ICCAR). New York, USA: IEEE, 2019: 545-549.
[21] GAO G, QIAN K, MA X, et al. Object recognition and augmentation for wearable-assistive system using egocentric RGB-D sensor[C]//2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER). New York, USA: IEEE, 2017: 775-780.
[22] 张晗, 康国华, 张琪, 等. 基于改进SAC-IA算法的激光点云粗配准[J]. 航天控制, 2019, 37(5): 67-74. https://www.cnki.com.cn/Article/CJFDTOTAL-HTKZ201905011.htm ZHANG H, KANG G H, ZHANG Q, et al. Laser point cloud coarse registration based on improved SAC-IA algorithm[J]. Aerospace Control, 2019, 37(5): 67-74(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HTKZ201905011.htm
[23] 朱琛琛, 齐林, 帖云. 基于弧长密度的自动邻域半径鉴别FPFH提取算法[J]. 计算机工程, 2019, 45(10): 253-259. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201910042.htm ZHU Ch Ch, QI L, TIE Y. Automatic neighborhood radius identification FPFH extraction algorithm based on arc length density[J]. Computer Engineering, 2019, 45(10): 253-259(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201910042.htm
计量
- 文章访问数: 8
- HTML全文浏览量: 1
- PDF下载量: 5