Research progress on quantum dispersion cancellation
-
摘要: 非局域色散消除是量子纠缠光源的非经典效应之一，在量子信息科学中有着重要的应用。详细介绍了非局域色散消除的概念、研究意义以及近几年国内外的发展状况。对频率纠缠光源的非局域色散消除、Franson干涉仪中的非局域色散消除、Hong-Ou-Mandel干涉仪中的局域色散消除等3种情况的研究进展进行了对比分析。在此基础上，对量子色散消除的研究前景进行了展望。Abstract: Nonlocal dispersion cancellation is one of the non-classical effects of quantum entangled photon sources, and it has important applications in quantum information science. A detailed introduction to the concept, research significance of nonlocal dispersion cancellation, and the research progress in China and abroad in recent years were reviewed. The following three cases: the nonlocal dispersion cancellation of frequency entangled photon sources, the nonlocal dispersion cancellation in Franson interferometers, and the local dispersion cancellation in the Hong-Ou-Mandel interferometer were then compared and analyzed. On this basis, the prospects for the study of quantum dispersion cancellation were anticipated.
-
引言
色散是指不同颜色的光经过介质之后，在时间上散开的现象。造成色散的原因在于介质的折射率是波长依赖的，不同颜色(由频率决定)光的速度不同，因而到达时间不同。色散是光学中常见的现象，虽然利用色散可以带来正面的应用，比如利用色散原理制作的传感器可以实现物体表面轮廓的高精度测量。但是，色散也往往给光学系统带来很多负面的影响，比如在光学成像中会导致成像分辨率的下降，在普通的光学测量中会导致测量精度的下降，在光纤通信中会导致相邻脉冲重叠、信号无法区分，从而影响通信质量。经典光学中两束光所经历的色散是无法彼此消除的。随着量子科技的发展，人们发现利用频率纠缠光子对(或称为能量-时间纠缠光子对)可以将两个光子所经历的色散非局域地消除掉，这一非经典的效应被称为非局域色散消除(nonlocal dispersion cancellation, NDC)。这一概念由FRANSON在1992年首次提出[1]，自其提出以来备受关注。本文中将详细讲述量子色散消除的相关研究进展。首先会阐述非局域色散消除的基本概念, 其次分析非局域色散消除的研究意义，然后对非局域色散消除的研究现状进行综述，最后介绍Hong-Ou-Mandel(HOM)干涉仪中局域色散消除的研究进展以及总结与展望。
1. 非局域色散消除的概念
非局域性是纠缠态所具有的典型量子特性，这种特性无法用经典理论或局域隐变量理论解释，它是量子力学的最本质的特征之一[2]。非局域色散消除是非局域性的表现形式之一。它是指频率纠缠光子对中的信号光s经历的色散可以被闲频光i经历的色散非局域消除掉，只要使两光子经过的色散量大小相等符号相反，无论这两个光子相距有多远，它们之间的符合信号(量子关联性)不会改变。就好像这两个光子没有经过色散介质一样。而换成经典脉冲，经上述色散介质后其符合信号仍然会被展宽。
通过自发参量下转换(spontaneous parametric down conversion, SPDC)过程产生频率纠缠光子对态函数的一般形式可以表示为:
|ψ⟩=∬ (1) 式中，ω表示光子的频率，下标s, i分别表示下转换产生的信号光和闲频光，F(ωs, ωi)为双光子光谱振幅， \hat{a}^{\dagger} 为产生算符，|0〉表示真空态。一般F(ωs, ωi)≠F(ωs)F(ωi)，即双光子光谱振幅是不可因子化的，因此是频率纠缠的。如图 1所示[3]，假设用连续激光抽运BBO晶体产生频率纠缠光子对，则(1)式中的态函数可以简化为：
\begin{gathered} |\psi\rangle= \\ \int \mathrm{d} \Omega F(\Omega) \hat{a}_{s}^{\dagger}\left(\omega_{0} / 2+\Omega\right) \hat{a}_{i}^{\dagger}\left(\omega_{0} / 2-\Omega\right)|0\rangle \end{gathered} (2) 式中，Ω=ωs, i-ω0/2为信号(闲频)光子与抽运中心频率ω0一半的偏移量。此态是最大频率纠缠态，且两双光子频率完全反关联。由于在SPDC过程中满足能量守恒，纠缠光子对的频率之和一定等于抽运光频率(是一个固定值)。因此，只要测量其中一个光子的频率，就可以同时精确确定另一个光子的频率。在下面会看到，这一特性决定了纠缠光子对的非局域色散消除效应。
如果让信号光s经过2阶色散系数为β1、长度为z1的色散介质后进入探测器D1得到光子到达时间t1，让闲频光i经过2阶色散系数为β2、长度为z2的色散介质后进入探测器D2得到光子到达时间t2, 则两个探测器的联合探测概率正比于以下的Glauber 2阶关联函数：
G^{(2)}\left(t_{1}, t_{2}\right)=\left|\left\langle 0\left|\hat{E}_{2}^{(+)}\left(t_{2}\right) \hat{E}_{1}^{(+)}\left(t_{1}\right)\right| \psi\right\rangle\right|^{2} (3) 式中， \hat{E}_{1}^{(+)}\left(t_{1}\right)=\int \mathrm{d} \omega_{1} f\left(\omega_{1}\right) \hat{a}_{1}\left(\omega_{1}\right) \exp \left[-\mathrm{i}\left(\omega_{1} t_{1}-\right.\right. \left.\left.k_{1} z_{1}\right)\right]是光场在探测器D1处的正频分量， \hat{\boldsymbol{E}}_{2}^{(+)}\left(t_{2}\right)的定义类似; 实验中，一般用滤波器对纠缠光谱进行后处理，滤波函数为f(ω)=exp[-(ω-ωf)2/(2σf2)]，其中，ωf为滤波的中心频率，σf为滤波器的带宽。假设滤波器的带宽很窄，可以将波数k用泰勒级数展开到2阶(忽略3阶和更高阶项)：kj(ω0±Ω)=kj(ω0)±αjΩ+βjΩ2, j=1, 2。其中，α和β分别表示色散介质的1阶和2阶色散系数，它们分别决定着波包的延迟和展宽[3]。经过计算最终得到：
G^{(2)}\left(t_{1}-t_{2}\right)=\operatorname{Cexp}\left[-\frac{\left(t_{1}-t_{2}-\tilde{t}\right)^{2}}{2 \sigma_{\mathrm{t}}^{2}}\right] (4) 式中，C为常数， \tilde{t}=\alpha_{2} z_{2}-\alpha_{1} z_{1}。实验时通常将探测的光子到达时间信号进行符合处理得到符合计数的分布，以此来反应G(2)的形状。理论上可以得到符合分布的方差数学表达式为[1, 4]：
\sigma_{\mathrm{t}}^{2}=\frac{1 / \sigma_{\mathrm{f}}^{4}+\left(\beta_{1} z_{1}+\beta_{2} z_{2}\right)^{2}}{1 / \sigma_{\mathrm{f}}^{2}} (5) (5) 式包含了色散系数和的平方，若β1z1=-β2z2, 则信号光s所经历的色散将被闲频光i所经历的色散非局域地消除。如果将上述纠缠光换成经典光源，则符合分布的方差数学表达式[1, 4]变成：
\sigma_{\mathrm{c}}^{2}=\frac{1 /\left(2 \sigma_{\mathrm{f}}^{4}\right)+\beta_{1}^{2} z_{1}^{2}+\beta_{2}^{2} z_{2}^{2}}{1 / 2 \sigma_{\mathrm{f}}^{2}} (6) (6) 式包含了色散系数平方的和，此时，两束经典光所经历的色散彼此间将无法消除。(5)式和(6)式差异的根本原因来自于频率纠缠光源的纠缠特性。
这一效应已分别在纳秒[3, 5-6]、皮秒[7]和飞秒[8-9]尺度被实验验证。需要说明的是，非局域色散消除必须使用非局域的探测方式，如果探测方式是局域的，则这种效应存在经典类比[10]。因此，非局域的探测方式是验证量子非局域性的必要条件。从这个角度来说，LI等人[7]和MAcLEAN等人[11]利用非局域的探测方法所做的工作才是真正意义上的非局域色散消除。而在HOM干涉中，参与干涉的光子需要在分束器上汇聚，因此其探测方式必然本质上是局域的，因而HOM干涉存在着经典类比[12-14]，而非局域色散消除是无法用经典过程来模拟的，不存在经典类比，它是量子力学的独特特征，无法用任何经典理论或基于决定论的定域隐变量理论来解释。
为了定量描述这种效应，2010年，WASAK等人[15]提出了一个判定非局域色散消除的不等式，其表达式可以写为：
\left\langle\left(\Delta \tau^{\prime}\right)^{2}\right\rangle \geqslant\left\langle(\Delta \tau)^{2}\right\rangle+\frac{(2 \beta L)^{2}}{\left\langle(\Delta \tau)^{2}\right\rangle} (7) 式中，〈(Δτ)2〉和〈(Δτ′)2〉分别表示未加色散和加大小相等正负相反色散后纠缠光子对到达时间差的方差。此时2阶色散系数β1=-β2=β，长度z1=z2=L。其归一化的表达式可以写为：
W=\frac{\left\langle\left(\Delta \tau^{\prime}\right)^{2}\right\rangle\left\langle(\Delta \tau)^{2}\right\rangle}{\left[\left\langle(\Delta \tau)^{2}\right\rangle\right]^{2}+(2 \beta L)^{2}} \geqslant 1 (8) 经典光场满足上述不等式，然而，频率纠缠光场将违背以上不等式。因此，此不等式类似于测试偏振纠缠非局域性所用的Bell不等式，可以作为经典光场和非经典(频率纠缠)光场的判定标准，也可以作为频率纠缠光源非局域性测试的标准。目前，此不等式已经被实验所验证[7, 11]。需要说明的是，类似地，频率正关联纠缠光子对也将违背以上不等式，只是〈(Δτ)2〉和〈(Δτ′)2〉应该改为纠缠光子对到达时间和的方差。
目前，非局域色散消除的研究可以分成两类: 一类是量子纠缠光源的色散消除，即两个光子在经历色散介质之后，时域宽度都被扩展了，但是它们的到达时间关联函数没有被展宽; 另一类是非局域量子干涉仪(Franson干涉仪[16])中的色散消除。
2. 非局域色散消除的研究意义
非局域色散消除在量子信息和精密测量领域中有很广泛的应用。由于能够消除介质色散的影响，因此可以减小符合信号的噪声[17]，从而提高量子时钟同步[18-21]等领域的测量精度和稳定度。非局域色散消除还可以作为量子密钥分配的基础[22-24]，从而实现高维量子秘钥分发和保障量子通信的安全性。另外，利用非局域色散消除对应的Wasak不等式，可以进行量子力学的基本特性如非局域性的测试[7]。这些广泛的应用使得非局域色散消除的研究非常有意义。
3. 非局域色散消除的研究进展
3.1 非局域色散消除的理论提出及早期实验
1992年，FRANSON首次提出了非局域色散消除的概念[1]。1998年，BRENDEL等人[5]首次在实验上展示了这一效应，他们利用处于零色散波长对称波长位置的纠缠光子对在同一段测试光纤中实现了色散消除。2009年，FRANSON对非局域色散消除的概念进行了进一步的澄清和整理，与量子局域色散消除、经典光的色散消除进行了对比分析[4]。
2009年，BAEK等人[3]在实验上证明了利用纠缠光子可以实现非局域色散消除。实验装置如图 2aλ1的中心值为896nm，带宽为28nm; 闲频光波长λ2的中心值为750nm，带宽为20nm; 使用1.6km的单模光纤将正色散β1引入到信号光中; 使用光栅对将负色散β2引入到闲频光中。最后，对两路光子做单光子计数和符合计数。图 2b中只引入正色散β1时的符合计数，半峰全宽(full width at half maximum, FWHM)值为3.861ns。图 2c中同时引入正色散β1和负色散β2时的符合计数，FWHM为2.436ns。通过比较图 2b和图 2c可知，信号光的正色散效果(即符合计数的峰变宽了)被闲频光的负色散效果给抵消了，符合计数的峰变窄了，这是非局域色散消除的显著特征。这项研究结果在基于光纤的量子通信和量子计算中有着重要的应用，例如，可以提高量子通信的信噪比，提高量子计算中量子态的保真度。
2011年，O’DONNELL等人[8]利用棱镜对控制色散大小和正负在实验上实现了飞秒量级的非局域色散消除。2013年，普渡大学的LUKENS等人[9]利用空间光调制器实现了更高阶(3阶~5阶)的非局域色散消除。2015年，HU等人[25]实验实现了多个频率通道的非局域色散消除。
3.2 非局域色散消除现象的2维直接表征
以前的实验对非局域色散消除现象的测试是通过测量符合计数得到的, 测量的结果是一个1维分布，即符合计数是信号光s和闲频光i的时间差的函数p=p(ts-ti)。但是，这样的刻画方法是间接而不全面的，如果能测量信号光s和闲频光i的2维联合分布，即p=p(ts, ti), 则能直接而全面地描述双光子的时间分布, 帮助人们深刻认识非局域色散消除现象的全貌。2018年，MAcLEAN等人[11]完成了对非局域色散消除现象的直接表征。该实验原理如图 3a所示，激光源的波长是775nm，经过BiBO倍频，再经过BiBO下转换之后，制备了波长为729nm和827nm能量-时间纠缠光子对。图 3b是实验装置图，采用扫描两个单色仪的方法测量纠缠光子的联合频率分布，测量精度达到了0.1nm; 采用频率上转换的方法来测量纠缠光子的联合时间分布，测量精度达到150fs。图 3c是初始的联合时间分布; 图 3d是让信号光子经历了0.0373ps2的正色散之后的联合时间分布; 图 3e是让闲频光子经过-0.0359ps2的负色散之后的联合时间分布; 图 3f是让信号光子经过0.0373ps2的正色散, 闲频光子经过-0.0359ps2的负色散后的联合时间分布图。在图 3c中, Δ(ts-ti)的值是0.162ps, 在图 3f中, Δ(ts-ti)的值是0.175ps。可见, 信号光子和闲频光子之间的时间差(即对角线方向上)基本保持不变，实现了色散消除的效果。所用色散的平均大小为β=0.0366ps2，将以上数据代入WASAK的不等式，发现不等式被违背。
3.3 在长距离光纤链路中的非局域色散消除效应
前面介绍的实验主要是在可见光波段或近红外波段的实验，或者是在实验室内进行的短距离实验。然而，要实现非局域色散消除效应的实际应用，必须在光通信波段在长距离光纤链路上开展这项实验。在这方面，国内的研究小组做了几项非常有意义的研究工作。如中国科学院国家授时中心DONG研究员带领的量子时间同步研究小组，清华大学ZHANG教授带领的研究小组等[24, 26-27]。2019年，国家授时中心的DONG团队利用基于事件计时器的非局域测量方法[26]，在62km光纤链路中实验验证了非局域色散消除效应，并验证了WASAK提出的不等式的违背(W=0.253±0.052 < 1，违背不等式14个标准差)，验证了能量-时间纠缠光子对的非局域性，为未来在长距离光纤通道和自由空间实现连续变量严格意义的量子力学非局域性验证提供了可行性[7]，其主要实验结果如图 4所示。图 4a是未加色散时的结果，符合分布的FWHM为37.6ps，换算成标准差为15.982ps, 因此得到〈(Δτ)2〉=(15.982ps±0.150ps)2; 图 4b~图 4d分别是在信号光路中单独加10km、20km、62km单模光纤(见三角点)及单独加对应1.245km、2.49km、7.47km色散补偿光纤(dispersion compensation fiber，DCF)(见圆点)和正负色散同时都加时的结果(见方点)。图 4d中色散消 除后的符合分布的FWHM为107.0ps，换算成标准差为45.676ps, 得到〈(Δτ′)2〉=(45.676ps±4.565ps)2; 两个路径中所加色散的平均值为2βL=1428.92ps2。图中蓝色三角代表只给信号光加色散，蓝色圆点代表只给闲频光加色散，红色方点代表两者都加，黑线为理论模拟结果。将这些数据代入归一化的Wasak不等式(见(8)式)可以得到：W=0.253±0.052 < 1。由于探测器的时间抖动(约37ps)，只有当色散量很大时(见图 4d中62km单模光纤(single mode fiber, SMF)) 才能违背Wasak不等式。实际中频率纠缠源的不完美(非最大纠缠)及探测器的时间抖动等因素对Wasak不等式违背的影响可见参考文献[28]。
![图 4 实验得到的符合分布[26]]()
图 4 实验得到的符合分布[26]a—未加色散 b~d—分别给信号光加10km/20km/62km单模光纤，给闲频光加1.245km/2.49km/7.47km色散补偿光纤时的结果同年，他们首次提出基于光纤的双向量子时间传递协议，并利用非局域色散消除效应在20km光纤链路中完成了实验演示，提高了时间传递的稳定度(45fs@40960s)。ZHANG团队基于非局域色散消除开展了量子安全鬼成像[27]和20km光纤上量子密钥分配(dispersive optics quantum key distribution, DO-QKD)[24]的实验研究。基于纠缠的DO-QKD可以高效、方便地实现，在未来的量子保密通信网络中具有很大的应用潜力。
3.4 非最大纠缠态非局域色散消除的最优方案
在之前NDC的理论研究中，研究的对象往往都是具有最大纠缠度的能量-时间纠缠态，利用这种最大纠缠态，可以实现色散的完全消除。但是，在实验中制备的纠缠态的纠缠度都是有限的，利用这种非最大纠缠态，不能实现色散的完全消除。因此很有必要考虑在非最大纠缠态的条件下，非局域色散消除的最优的方案是怎样的，该方案可以在多大程度上消除色散？针对这一问题，2020年，XIANG等人[28]首先在理论上对NDC的模型进行了完整的分析，然后在实验上制备了频域正关联和反关联的两种纠缠态对理论进行了验证。实验装置如图 5a所示，频率正关联光子对和反关联的双光子源是通过SPDC过程在Ⅱ型PPKTP晶体中产生的[29-32]，偏振正交的信号光s和闲频光i被光纤偏振分束器(fiber polarizing beam splitter, FPBS)分成两路，信号光一路通过SMF; 闲频光一路通过DCF或SMF。然后通过超导纳米线单光子探测器(superconductive nanowire single photon detectors, SNSPD)探测，最后由两个单独的事件计时器(event timers, ET)分别记录为时间序列，由电脑来分析符合计数。图 5b显示了在使用频率反关联的双光子的情况下，符合计数宽度随闲频光一路中DCF长度的变化关系; 图 5c显示了频率正关联的双光子，符合计数宽度随闲频光一路中的DCF长度的关系。图 5b和图 5c中的最低点就对应了最优的色散消除方案。基于本方案，目前NDC已经被应用于非局域性(Wasak不等式)的测试[7]、量子时间传递[21]。
3.5 3个及更多光子的非局域色散消除
2020年，FRANSON小组[33]在理论上把NDC的概念扩展到3个及更多光子的情况。该理论方案图如图 6a所示。利用3阶非线性晶体的SPDC过程，把一个高频抽运光子(频率为ω0)转换成3个低频光子(频率为ω1, ω2, ω3)，3个光子在能量-时间维度上纠缠。首先让3个光子分别通过带宽为σf的BPF进行过滤，然后通过3段色散系数分别为β1, β2, β3的介质, 传播了x1, x2, x3的距离，最后考察三端符合计数与到达时间/传输距离/色散系数之间的关系，并将量子光与经典光的情况进行了对比，对比的结果如图 6b和图 6c所示。图 6b是量子光的情况，图 6c是经典光的情况。横轴τ是第3个光子与第2个光子之间的到达时间差。纵轴t是第2个光子与第1个光子之间的到达时间差。颜色代表三端符合计数的概率。可见，选定的参量条件下，量子光源可以获得很好的色散消除效果，而经典光源却不能实现色散消除。该研究结果对于在3个或更多节点的网络中实现量子密钥分发的应用具有重要价值。
3.6 Franson干涉仪中的非局域色散消除
2013年，ZHONG等人[34]在理论和实验上展示了Franson干涉仪中的非局域色散消除。实验装置如图 7a所示，从Ⅱ型匹配的PPKTP波导中制备了信号光和闲频光，然后两个光子被分别送入两个不等臂的马赫-曾德尔(Mach-Zehnder，MZ)干涉仪中，其中在上面一路的长臂中加入了2.2×10-2ps2的正色散，在下面一路的长臂中加入了-2.2×10-2ps2的负色散，最后两路光子被送入单光子探测器，并使用符合计数器进行时间关联分析。实验结果如图 7b所示，与没有采用色散消除的方案相比，采用了色散消除的方案可以让Franson干涉仪的干涉度获得提高。例如，在α值(平均每个脉冲中包含光子对的比例)为0.24%时，干涉度从98.2%提高到了99.6%。随着α值增大，干涉度会降低，但是采用了色散消除的干涉度总是比没有色散消除时候的干涉度要高。该方案可以应用于基于高维时间-能量纠缠的量子密钥分发协议，提高安全密钥率[35]。
4. HOM干涉仪中的局域色散消除研究进展
4.1 HOM干涉仪中的局域色散消除
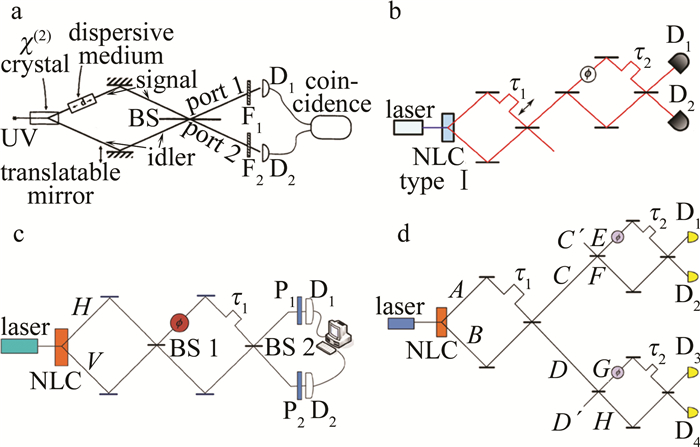
HOM干涉仪[36]是量子光学中非常重要的量子干涉仪，目前已经在量子信息与量子计算的研究中获得广泛应用。在HOM干涉中，也存在色散消除的效应，这方面的工作在1992年由STEINBERG等人[37]首次提出，其理论模型如图 8a所示，该研究表明，如果在HOM干涉仪的一臂中加入色散介质，那么干涉条纹会发生平移，但是偶数阶的色散成分不会造成条纹展宽，只有奇数阶的色散成分会造成色散条纹展宽，即偶数阶的色散被消除; 如果给HOM干涉仪的两臂都加入同样的介质，奇数和偶数阶的色散成分都不会造成条纹展宽，即所有阶的色散都会被消除。该色散消除方案目前已经被应用于高精度的量子时钟同步[18]和分辨率增强的量子相干层析[38]。为了在一臂加入色散的时候同时消除奇数阶和偶数阶的色散，2009年, MINAEVA等人[39]基于HOM干涉仪提出了一个改进的理论方案，如图 8b所示，基于该方案可以在一个干涉条纹的不同区域实现奇数和偶数阶的色散消除。2015年，QIU等人[40]在HOM型干涉仪的基础上再多加一个分束器，并且在最后的两个探测器上各加一个偏振片，如图 8c所示，通过设定偏振片的角度，也可以实现奇数和偶数阶的色散消除。另外，QIU等人[41]还提出了基于4个光子干涉的色散消除方案，如图 8d所示，研究发现，在4个光子的干涉中，也可以观测到奇数和偶数阶的色散消除，更有趣的是发现4个光子的干涉条纹更窄，因此其对应的测量分辨率更高。
![图 8 HOM干涉仪中的局域色散消除]()
需要指出的是，HOM干涉仪中的色散消除，存在着经典对应[12-14]，即在某些特定条件下，经典光源也可以实现HOM干涉的色散消除。此外，双光子在干涉前需要在分束器上重新汇合，然后探测，这种探测属于局域探测。因此，HOM干涉仪中的色散消除不具有非局域性。与之不同的是，Franson干涉中的色散消除是非局域的。
4.2 独立单光子源HOM干涉中的局域色散消除
量子信息处理的一项关键技术是在独立的单个光子之间获得高可见度的量子干涉。影响量子干涉的关键因素之一是当单个光子通过色散介质时发生的群速度色散。2021年，IM等人[42]研究了独立单光子源HOM干涉过程中的局域色散消除情况，实验装置如图 9a所示，首先从两个BBO晶体中制备了两个独立的宣布式单光子源，接着让两路光子分别经过长度为L1和L2，色散系数为β1和β2的色散介质，然后通过一个分束器(beam splitter，BS)进行干涉，最后进行单光子探测和符合计数。实验结果如图 9b所示，如果两个单光子源之间经历了相同的色散值，那么HOM干涉条纹的干涉度可以达到100%;干涉条纹的时域宽度会保持最窄的值，约0.4ps。如果增加两路之间的色散差，干涉度会逐渐从100%下降到低于20%，干涉条纹的宽度会从约0.4ps扩宽到1.3ps。该工作还在理论上考虑了3路独立单光子源及更多路独立单光子源HOM干涉的色散消除条件。总之，该工作在理论和实验上证明了，如果两个独立的单光子经历相同数量的脉冲展宽，则可以消除群速度色散对双光子干涉的影响。
4.3 相干光源HOM干涉中的局域色散消除
2021年，FAN等人[43]在理论和实验上研究了相干光源HOM干涉中的色散效应。实验原理图和装置图如图 10a和图 10b所示，采用的激光脉冲的中心波长为1548.74nm，频域宽度为3.48nm(时域宽度为1.12ps)，重复周期为25ns(重复频率为40MHz)，经衰减，获得平均每个脉冲的光子数是0.007。图 10c是没有经历色散的HOM干涉图，干涉度为50.2%，FWHM为1.31ps。图 10d是经历了50km单模光纤色散后的HOM干涉图。虽然光脉冲被从约1.12ps展宽到了3.4ns，但是HOM的干涉度和宽度几乎不变，测量值为47.2%和1.31ps。这表明, 如果参与HOM干涉的两路光经历了相同的色散，则干涉条纹不会被展宽。进一步实验表明, 如果两路经历的不同的色散，那么干涉条纹会被展宽。该研究不仅加深了人们对相干光HOM干涉的认识，而且可以用来测试经历色散之后光脉冲的原始宽度，也可以用来测试未知光学材料的色散系数。相干光的色散消除效果与参考文献[42]中独立单光子源之间HOM干涉中的色散消除效应有相似之处。值得强调的是，该工作从色散的角度探讨了单光子波包的基本特性，研究了色散对单光子波包全同性的影响，并使用相干态光子波包进行了原理性的实验验证。
5. 结束语
本文中全面分析了量子色散消除的研究进展。可以看出，量子色散消除是一个富有研究价值的领域，其拥有许多潜在的应用; 同时该领域也是一个蓬勃发展的领域，近3年来涌现出了很多新的重要成果。
展望未来，这个领域有可能朝以下方向发展：
(1) 在光源方面，三光子纠缠及更多光子纠缠光源的非局域色散消除值得探索。目前人们在理论和实验上研究了双光子的色散消除，这只是一个两体相互作用问题，而三光子纠缠属于三体相互作用问题，其包含了更丰富的物理内容。在三光子纠缠方面，目前已经有了初步的理论研究，但在实验方面尚无报道，值得深入探索。
(2) 在新的自由度方面，值得扩展。目前量子色散消除仅研究了频率和时间这两个自由度。受此启发，最近人们提出了在空间自由度和偏振自由度方面的模式消除，如非局域像差消除和非局域偏振模式消除[44-46]，其原理类似于频率域的色散消除。
(3) 在量子技术方面，如何把非局域色散消除应用起来，是未来的重要发展方向。目前在生物成像方面，人们已经可以利用NDC提高成像的分辨率; 在量子密钥分配方面，可以利用色散消除提高量子密钥分配的安全性和成码率[24, 47-49]。未来期待色散消除可以推广到更多领域。
-
![]()
图 4 实验得到的符合分布[26]
a—未加色散 b~d—分别给信号光加10km/20km/62km单模光纤，给闲频光加1.245km/2.49km/7.47km色散补偿光纤时的结果
![]()
-
[1] FRANSON J D. Nonlocal cancellation of dispersion[J]. Physical Review, 1992, A45(5): 3126-3132. http://www.onacademic.com/detail/journal_1000036100160010_0e94.html
[2] CHEN Zh, HAN Y J. Quantum nonlocality, quantum entanglement and new physics[J]. Chinese Science Bulletin, 2016, 61(10): 1072-1074. DOI: 10.1360/N972016-00123
[3] BAEK S Y, CHO Y W, KIM Y H. Nonlocal dispersion cancellation using entangled photons[J]. Optics Express, 2009, 17(21): 19241-19252. DOI: 10.1364/OE.17.019241
[4] FRANSON J D. Nonclassical nature of dispersion cancellation and nonlocal interferometry[J]. Physical Review, 2009, A80(3): 032119.
[5] BRENDEL J, ZBINDEN H, GISIN N. Measurement of chromatic dispersion in optical fibers using pairs of correlated photons[J]. Optics Communications, 1998, 151(1/3): 35-39. http://unige.ch/gap/qtech/_media/publications:bib:2_photoncd.pdf
[6] JARAMILLO-VILLEGAS J A, IMANY P, ODELE O D, et al. Persistent energy-time entanglement covering multiple resonances of an on-chip biphoton frequency comb[J]. Optica, 2017, 4(6): 655-658. DOI: 10.1364/OPTICA.4.000655
[7] LI B H, HOU F Y, QUAN R A, et al. Nonlocality test of energy-time entanglement via nonlocal dispersion cancellation with nonlocal detection[J]. Physical Review, 2019, A100(5): 053803. http://arxiv.org/abs/1906.03769v2
[8] O'DONNELL K A. Observations of dispersion cancellation of entangled photon pairs[J]. Physical Review Letters, 2011, 106(6): 063601. DOI: 10.1103/PhysRevLett.106.063601
[9] LUKENS J M, DEZFOOLIYAN A, LANGROCK C, et al. Demonstration of high-order dispersion cancellation with an ultrahigh-efficiency sum-frequency correlator[J]. Physical Review Letters, 2013, 111(19): 193603. DOI: 10.1103/PhysRevLett.111.193603
[10] PREVEDEL R, SCHREITER K M, LAVOIE J, et al. Classical a-nalog for dispersion cancellation of entangled photons with local detection[J]. Physical Review, 2011, A84(5): 051803. http://homepage.univie.ac.at/robert.prevedel/images/Franson_disp_paper.pdf
[11] MAcLEAN J P W, DONOHUE J M, RESCH K J. Direct characte-rization of ultrafast energy-time entangled photon pairs[J]. Physical Review Letters, 2018, 120(5): 053601. DOI: 10.1103/PhysRevLett.120.053601
[12] KALTENBAEK R, LAVOIE J, BIGGERSTAFF D N, et al. Quantum-inspired interferometry with chirped laser pulses[J]. Nature Physics, 2008, 4(11): 864-868. DOI: 10.1038/nphys1093
[13] KALTENBAEK R, LAVOIE J, RESCH K J. Classical analogues of two-photon quantum interference[J]. Physical Review Letters, 2009, 102(24): 243601. DOI: 10.1103/PhysRevLett.102.243601
[14] LAVOIE J, KALTENBAEK R, RESCH K J. Quantum-optical coherence tomography with classical light[J]. Optics Express, 2009, 17(5): 3818-3826. DOI: 10.1364/OE.17.003818
[15] WASAK T, SZAN'KOWSKI P, WASILEWSKI W, et al. Entanglement-based signature of nonlocal dispersion cancellation[J]. Physical Review, 2010, A82(5): 052120. http://www.onacademic.com/detail/journal_1000034861699910_4293.html
[16] FRANSON J D. Bell inequality for position and time[J]. Physical Review Letters, 1989, 62(19): 2205-2208. DOI: 10.1103/PhysRevLett.62.2205
[17] FITCH M J, FRANSON J D. Dispersion cancellation and nonclassical noise reduction for large-photon-number states[J]. Physical Review, 2002, A65(5): 053809. http://core.ac.uk/download/pdf/2652679.pdf
[18] GIOVANNETTI V, LLOYD S, MAcCONE L, et al. Clock synchronization with dispersion cancellation[J]. Physical Review Letters, 2001, 87(11): 117902. DOI: 10.1103/PhysRevLett.87.117902
[19] GIOVANNETTI V, LLOYD S, MAcCONE L. Quantum-enhanced measurements: Beating the standard quantum limit[J]. Science, 2004, 306(5700): 1330-1336. DOI: 10.1126/science.1104149
[20] VALENCIA A, SCARCELLI G, SHIH Y. Distant clock synchronization using entangled photon pairs[J]. Physical Review Letters, 2004, 85(13): 2655-2657. http://www.onacademic.com/detail/journal_1000037122882810_eba6.html
[21] HOU F Y, QUAN R A, DONG R F, et al. Fiber-optic two-way quantum time transfer with frequency-entangled pulses[J]. Physical Review, 2019, A100(2): 023849. http://www.researchgate.net/publication/335485515_Fiber-optic_two-way_quantum_time_transfer_with_frequency-entangled_pulses
[22] MOWER J, ZHANG Z, DESJARDINS P, et al. High-dimensional quantum key distribution using dispersive optics[J]. Physical Review, 2013, A87(6): 062322. http://www.researchgate.net/profile/Jacob_Mower/publication/232252992_High-Dimensional_Quantum_Key_Distribution_using_Dispersive_Optics/links/00b4953a05229082be000000.pdf
[23] LEE C, ZHANG Zh Sh, STEINBRECHER G R, et al. Entanglement-based quantum communication secured by nonlocal dispersion cancellation[J]. Physical Review, 2014, A90(6): 062331. http://perso-etis.ensea.fr/ligong.wang/papers/2014_PRA.pdf
[24] LIU X, YAO X, WANG H Q, et al. Energy-time entanglement-based dispersive optics quantum key distribution over optical fibers of 20km[J]. Applied Physics Letters, 2019, 114(14): 141104. DOI: 10.1063/1.5089784
[25] HU X L, ZHONG T, WONG F N C, et al. Nonlocal cancellation of multi-frequency-channel dispersion[J]. Physical Review, 2015, A91(1): 013809. http://www.researchgate.net/profile/Tian_Zhong5/publication/273176312_Nonlocal_cancellation_of_multi-frequency-channel_dispersion/links/5650d1db08ae4988a7aba9d9.pdf
[26] QUAN R A, DONG R F, XIANG X, et al. High-precision nonlocal temporal correlation identification of entangled photon pairs for quantum clock synchronization[J]. Review of Scientific Instruments, 2020, 91(12): 123109. DOI: 10.1063/5.0031166
[27] YAO X, LIU X, YOU L X, et al. Quantum secure ghost imaging[J]. Physical Review, 2018, A98(6): 063816.
[28] XIANG X, DONG R F, LI B H, et al. Quantification of nonlocal dispersion cancellation for finite frequency entanglement[J]. Optics Express, 2020, 28(12): 17697-17707. DOI: 10.1364/OE.390149
[29] QUAN R A, WANG M M, HOU F Y, et al. Characterization of frequency entanglement under extended phase-matching conditions[J]. Applied Physics, 2015, B118(3): 431-437. http://www.onacademic.com/detail/journal_1000038007331110_1e3b.html
[30] HOU F Y, XIANG X, QUAN R A, et al. An efficient source of frequency anti-correlated entanglement at telecom wavelength[J]. Applied Physics, 2016, B122(5): 128-136. http://www.onacademic.com/detail/journal_1000038830365310_91c7.html
[31] JIN R B, SHIMIZU R, WAKUI K, et al. Widely tunable single photon source with high purity at telecom wavelength[J]. Optics Express, 2013, 21(9): 10659-10666. DOI: 10.1364/OE.21.010659
[32] JIN R B, ZHAO P, DENG P G, et al. Spectrally pure states at telecommunications wavelengths from periodically poled MTiOXO4 (M= K, Rb, Cs; X= P, As) crystals[J]. Physical Review Applied, 2016, 6(6): 064017. DOI: 10.1103/PhysRevApplied.6.064017
[33] NODURFT I C, SHRINGARPURE S U, KIRBY B T, et al. Nonlocal dispersion cancellation for three or more photons[J]. Physical Review, 2020, A102(1): 013713. http://arxiv.org/abs/2003.13688
[34] ZHONG T, WONG F N C. Nonlocal cancellation of dispersion in Franson interferometry[J]. Physical Review, 2013, A88(2): 020103. http://www.onacademic.com/detail/journal_1000037103079510_0c56.html
[35] ZHONG T, WONG F N C, RESTELLI A, et al. Efficient single-spatial-mode periodically-poled KTiOPO4 waveguide source for high-dimensional entanglement-based quantum key distribution[J]. Optics Express, 2012, 20(24): 26868-26877. DOI: 10.1364/OE.20.026868
[36] HONG C K, OU Z Y, MANDEL L. Measurement of subpicosecond time intervals between two photons by interference[J]. Physical Review Letters, 1987, 59(18): 2044-2046. DOI: 10.1103/PhysRevLett.59.2044
[37] STEINBERG A M, KWIAT P G, CHIAO R Y. Dispersion cancellation and high-resolution time measurements in a fourth-order optical interferometer[J]. Physical Review, 1992, A45(9): 6659-6665. http://www.onacademic.com/detail/journal_1000037061728010_8af9.html
[38] NASR M B, SALEH B E A, SERGIENKO A V, et al. Demonstration of dispersion-canceled quantum-optical coherence tomography[J]. Physical Review Letters, 2003, 91(8): 083601. DOI: 10.1103/PhysRevLett.91.083601
[39] MINAEVA O, BONATO C, SALEH B E A, et al. Odd- and even-order dispersion cancellation in quantum interferometry[J]. Physical Review Letters, 2009, 102(10): 100504. DOI: 10.1103/PhysRevLett.102.100504
[40] QIU J, PAN J S, XIANG G Y, et al. Even- and odd-order dispersion cancellation effects in a two-photon interferometer[J]. Journal of the Optical Society of America, 2015, B32(5): 907-911. http://or.nsfc.gov.cn/bitstream/00001903-5/485227/1/1000013528301.pdf
[41] QIU J, XIANG G Y, ZHANG Y Sh, et al. Even- and odd-order dispersion cancellation effects in four-photon quantum interferometry[J]. Chinese Optics Letters, 2014, 12(11): 112701. DOI: 10.3788/COL201412.112701
[42] IM D G, KIM Y, KIM Y H. Dispersion cancellation in a quantum interferometer with independent single photons[J]. Optics Express, 2021, 29(2): 2348-2363. DOI: 10.1364/OE.415610
[43] FAN Y R, YUAN Ch Zh, ZHANG R M, et al. Effect of dispersion on indistinguishability between single-photon wave-packets[J]. Photonics Research, 2021, 9(6): 1134-1143. DOI: 10.1364/PRJ.421180
[44] BLACK A N, GIESE E, BRAVERMAN B, et al. Quantum nonlocal aberration cancellation[J]. Physical Review Letters, 2019, 123(14): 143603. DOI: 10.1103/PhysRevLett.123.143603
[45] BONATO C, SERGIENKO A V, SALEH B E A, et al. Even-order aberration cancellation in quantum interferometry[J]. Physical Review Letters, 2008, 101(23): 233603. DOI: 10.1103/PhysRevLett.101.233603
[46] SHTAIF M, ANTONELLI C, BRODSKY M. Nonlocal compensation of polarization mode dispersion in the transmission of polarization entangled photons[J]. Optics Express, 2011, 19(3): 1728-1733. DOI: 10.1364/OE.19.001728
[47] MAZUREK M D, SCHREITER K M, PREVEDEL R, et al. Dispersion-cancelled biological imaging with quantum-inspired interferometry[J]. Scientific Reports, 2013, 3(1): 1-5. http://www.scienceopen.com/document_file/bf2c6706-a8cc-4fb0-b314-50592ebf35b5/PubMedCentral/bf2c6706-a8cc-4fb0-b314-50592ebf35b5.pdf
[48] LIU X, YAO X, XUE R, et al. An entanglement-based quantum network based on symmetric dispersive optics quantum key distribution[J]. APL Photonics, 2020, 5(7): 076104. DOI: 10.1063/5.0002595
[49] LIU J Y, LIU X, ZHANG W, et al. The impact of fiber dispersion on the performance of entanglement-based dispersive optics quantum key distribution[J]. Journal of Electronic Science and Technology, 2021, 19(4): 100119. DOI: 10.1016/j.jnlest.2021.100119
-
期刊类型引用(0)
其他类型引用(1)
下载:
![图 2 使用纠缠光子的非局域色散消除[3]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-2.jpg)
![图 3 非局域色散消除现象的2维直接表征[11]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-3.jpg)
![图 4 实验得到的符合分布[26]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-4.jpg)
![图 5 非最大纠缠态非局域色散消除的最优方案研究[28]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-5.jpg)
![图 6 3个光子的非局域色散消除[33]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-6.jpg)
![图 7 Franson干涉仪中的非局域色散消除方案[34]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-7.jpg)
![图 9 独立单光子源HOM干涉中的色散消除实验[42]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-9.jpg)
![图 10 相干光源HOM干涉中的色散消除实验[43]](/fileJGJS/journal/article/jgjs/2022/1/jgjs-46-1-69-10.jpg)
计量
- 文章访问数: 11
- HTML全文浏览量: 4
- PDF下载量: 17
- 被引次数: 1