Design of self-similar pulse compression fiber based on chirp compensation technology
-
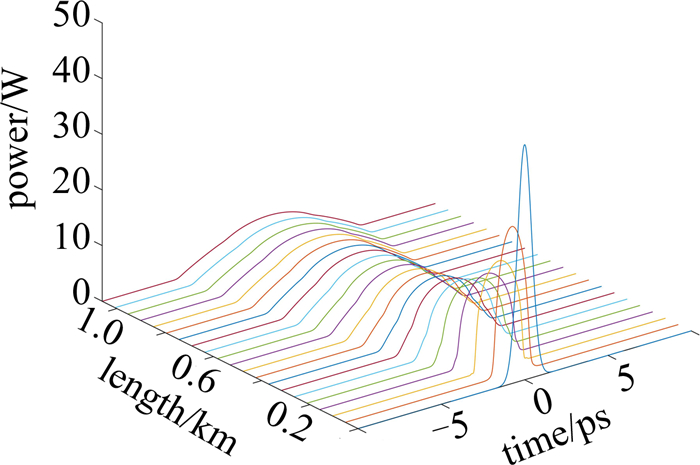
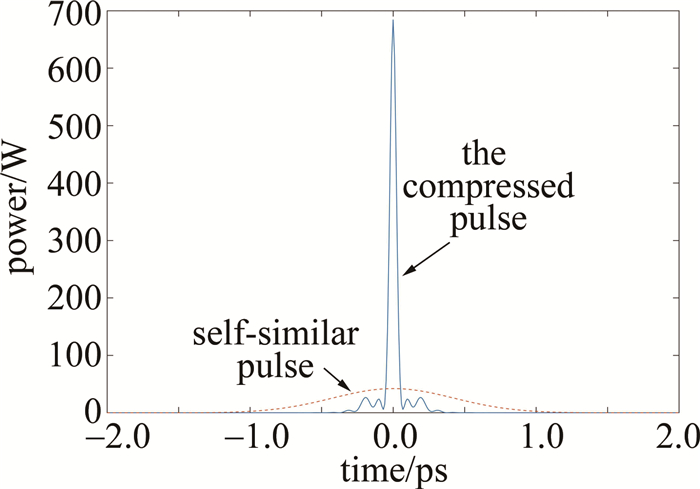
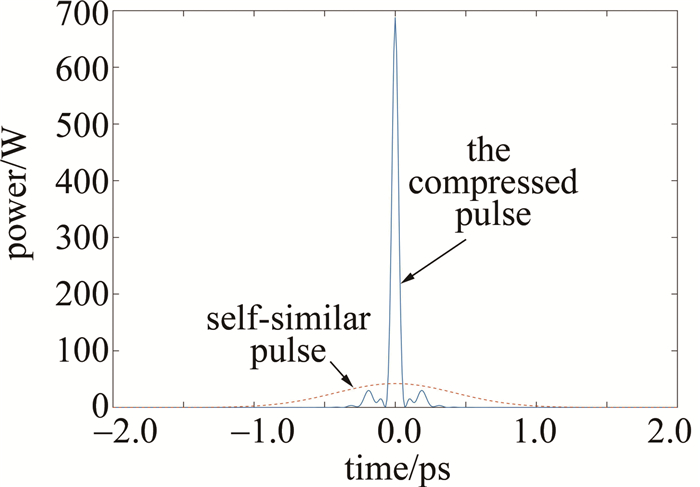
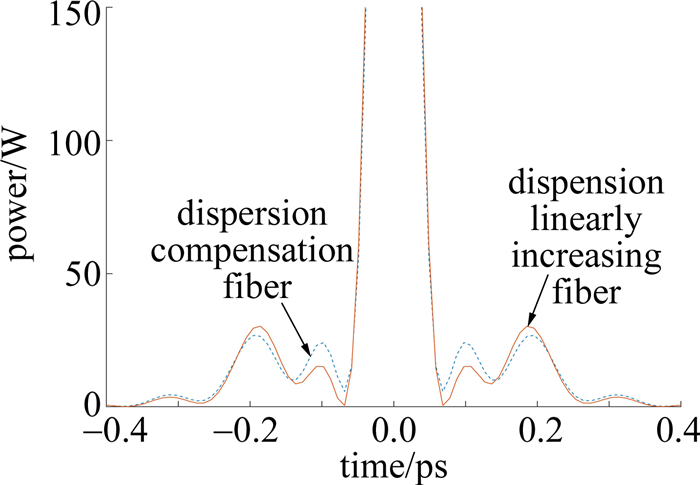
摘要: 为了获得高功率优质的超短脉冲光源,利用色散渐增光纤产生的强线性啁啾对自相似脉冲进行了啁啾补偿光纤设计。首先利用色散补偿光纤得到了半峰全宽为52.6fs、峰值功率为684.5W的超短脉冲输出。在此基础上研究了色散渐增的补偿光纤设计,讨论了色散线性渐增光纤和色散指数渐增光纤对自相似脉冲的压缩影响。当色散渐增系数取1km-1,5km-1,10km-1时,通过数值仿真得出了最短的输出脉宽、峰值功率以及所需的补偿光纤长度。结果表明,色散渐增光纤能缩短补偿光纤的长度,减小脉冲压缩时产生的损耗,得到半峰全宽为61.8fs和64.4fs的高功率超短脉冲输出。这一结果对自相似脉冲压缩光纤的设计是有帮助的。Abstract: In order to obtain high power and high quality ultrashort pulse light source, the chirp compensation fiber design of self-similar pulse was studied for the first time using strong linear chirp generated by the dispersion decreasing fiber (DDF). Firstly, the ultra-short pulse output with half height full width of 52.6fs and peak power of 684.5W was obtained by using dispersion compensation fiber. On this basis, the design of dispersion increasing compensation fiber was studied, and the effects of dispersion-linear-increased fiber and dispersion-exponential-increased fiber on the compression of self-similar pulses were emphatically discussed. When the dispersion increasing coefficient was respectively set to 1km-1, 5km-1, 10km-1, the shortest output pulse width, peak power and the required compensated fiber length were obtained by numerical simulation. The results show that the dispersion increasing fiber can shorten the length of the compensated fiber greatly, which is beneficial to reduce the loss caused by pulse compression, and finally obtain high power ultrashort pulse output with half height full width of 61.8fs and 64.4fs. This result is helpful to the design of self-similar pulse compression fiber.
-
Keywords:
- fiber optics /
- dispersion increasing fiber /
- chirp compensation /
- self-similar pulse
-
引言
光子晶体(photonic crystal,PC)具有操纵光子和控制光波传输的能力,但光在其中传播仍有一定的散射和损耗。将拓扑态引入光子系统中[1],革新了传统光波的传输和控制。受拓扑保护的光子器件具有强鲁棒性,可对结构缺陷免疫,但由于衍射极限的存在使得器件的微型化受到工程限制。石墨烯是由单层碳原子经sp2杂化组成的新型2维纳米材料[2],具有独特的电学和光学特性[3-5],可充当一种实现量子霍尔效应的理想平台,在纳米量级尺度上实现拓扑保护的光子态。表面等离子体有很强的局域性,可突破衍射极限,为实现纳米尺寸的光电器件和全光集成电路提供了可能[6-9]。与传统的贵金属相比,将石墨烯作为表面等离激元材料不仅成本更低,还具有可调性等许多优点。
2009年,OCHIAI等人[10]在石墨烯蜂窝晶格光子晶体中讨论了狄拉克点、拓扑边界等内容,并研究了其拓扑相变。2013年,KHANIKAEV等人[11-12]通过实验使2维光子拓扑绝缘体和光的量子自旋霍尔效应得以实现。2015年,CONSTANT等人[13]在石墨烯中通过红外光的近场散射激发表面等离子体激元。2016年,SLOBOZHANYUK等人[14]设计了一种超材料光子晶体,具有工程各向异性,实现了拓扑保护态,并证明了拓扑结构下的强鲁棒性和无背向散射的特性。2017年,MA等人[15]用数值方法研究了石墨烯和1维光子晶体的复合结构对光波的吸收属性,发现复合结构吸收谱具有类似1维光子晶体通带结构的吸收带结构。2018年,LU等人[16]基于3-D磁性Weyl光子晶体,设计了一种单向光纤的传输模式,通过打破了时间反演对称性,实现了拓扑保护。同年,SONG[17]基于石墨烯提出了拓扑光子晶体平板结构,实现拓扑边界态并验证其鲁棒性,证明了此结构在60THz~120THz范围的可调谐性。2019年,GAO等人[18]实现了光子晶体拓扑边界态光子自旋引导机制的光波导,有效提高了波导的传输效率,加强了波导结构的光子局域性,抑制背向散射,实现鲁棒性好的单向拓扑传输。2020年,HAN等人[19]基于石墨烯在中红外和太赫兹波段可以产生表面等离激元,设计了一种共振可调结构,从而在纳米尺度上有效控制石墨烯与光的相互作用。同年,BI等人[20]发明了一种硅基集成基于拓扑保护机理的光隔离器件,通过拓扑平台结构,有效减小了器件体积,且具有较小损耗等优势。
综上所述,光学拓扑态的实现可更好地控制光在特定通道内进行传播,同时具有高传输效率和低损耗的优势,引入石墨烯等离子体为把光集中在纳米尺度进行研究提供了依据。本文中基于石墨烯等离子体,提出一种新型2维光子晶体结构,通过调节一个周期内两个石墨烯圆盘的直径大小,最终实现拓扑边界传输态。研究结果可为在纳米量级设计具有对结构缺陷免疫的可调谐光子传输器件提供理论依据,给光学器件领域的研究注入新的活力。
1. 理论分析与计算
空间反演对称性和时间反演对称性保护着狄拉克锥,但当任意一个被破坏时,狄拉克简并将被打开,产生拓扑带隙。
量子霍尔效应基于时间反演对称性被破坏,用第一陈数C来描述此系统情况下的拓扑性质,其表征整数量子霍尔效应的拓扑不变量,它只能在能隙闭合的地方才会改变。引入Z2不变量[10]表征具有时间反演对称性系统的拓扑性质:
{Z_2} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\left[ {\oint\limits_{\partial {B^ + }} A (\mathit{\boldsymbol{k}}){\rm{d}}l - \int_{{B^ + }} \mathit{\boldsymbol{\Omega }} (\mathit{\boldsymbol{k}}){\rm{d}}{k^2}} \right]\, \bmod \, 2 (1) 式中,k是波矢, A(k)是贝里联络,Ω(k)是贝里曲率,B+表示半个布里渊区[21],∂B+为沿着半个布里渊区B+的边界,dl表示在半个布里渊区里的路径积分微元,mod 2表示除以2取余数,Z2=0为普通绝缘体,Z2=1为拓扑绝缘体。
在霍尔电导实验中,垂直电导Rxx=零,霍尔电阻Rxy确定为定值量子化常数RH=h/ve2,v为填充数。对于整数量子霍尔效应,霍尔电导为:
{\sigma _{xy}} = N\frac{{{e^2}}}{h} = N/(25812.807572\Omega ) (2) 式中,h是普朗克常数,e是电子电荷,N为正整数。
本文中采取调节石墨烯圆盘的直径大小来破坏晶格的时间反演对称性来打开狄拉克点,获得拓扑带隙,产生具有免疫结构缺陷和背向散射的拓扑边界保护态。
为控制同一周期内两个石墨烯圆盘的化学势一致,运用单层石墨烯上横向磁(transverse magnetic,TM)模的色散关系,在的非延迟体系中β»k0,即:
\beta = {\varepsilon _0}\frac{{{\varepsilon _{{\rm{air }}}} + {\varepsilon _{{\rm{Si}}{{\rm{O}}_2}}}}}{2}\frac{{2{\rm{i}}\omega }}{{{\sigma _{\rm{g}}}}} (3) 式中,εair=1,εSiO2=3.9,分别是空气和二氧化硅的介电常数,对应于本研究中的表层材料和基底材料,ε0是自由空间的真空介电常数,k0=ω/c为自由空间中的波数,β是在表面等离子体激元在石墨烯层上的传播常数,σg为石墨烯的表面电导率,ω是等离激元的角频率,c是光速。
而石墨烯的带间电导率为:
{\sigma _{{\rm{inter }}}} = \frac{{i{e^2}}}{{4{\rm{ \mathsf{ π} }}\hbar }}\ln \left[ {\frac{{2\left| {{\mu _{\rm{c}}}} \right| - \hbar (\omega + {\rm{i}}/\tau )}}{{2\left| {{\mu _{\rm{c}}}} \right| + \hbar (\omega + {\rm{i}}/\tau )}}} \right] (4) 式中,\hbar 是还原的普朗克常数,μc是化学势,τ是电子动量弛豫时间。
由上式可知,可通过施加外部电压来控制两个石墨烯圆盘的化学势保持相同。基于控制变量法,仅调节两个石墨烯圆盘的直径大小来破坏时间反演对称性。
2. 石墨烯光子晶体结构
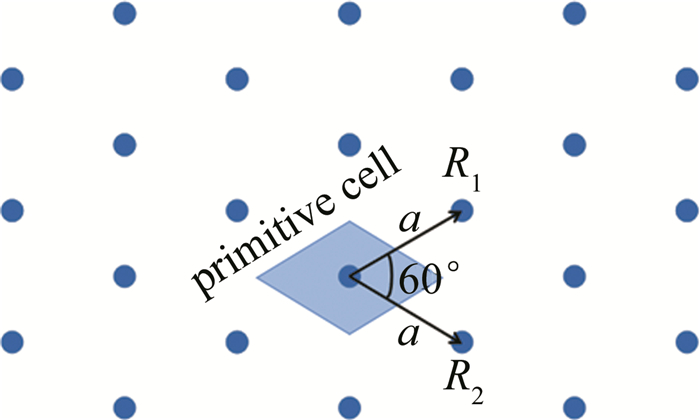
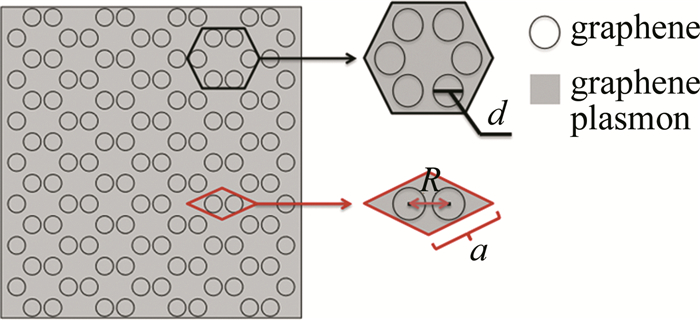
本文中提出一种周期性蜂窝状石墨烯表面等离激元光子晶体结构。通过设置晶格常数a=50nm,石墨烯圆盘直径d=0.42a,石墨烯圆盘圆心之间的距离R=31/2a/3,构建出三角晶格的六格点原胞,如图 1中正六边形所示,蜂巢晶格的初始两格点原胞如图 1中菱形所示。为增加对称性,提高简并度,以包含两个石墨烯盘的菱形晶格为一个周期。其中3-D基底可采用SiO2材料,平面上的基底为石墨烯等离子体,周期性排列于基底上的圆盘均为石墨烯材料,共同组成蜂巢光子晶体结构。
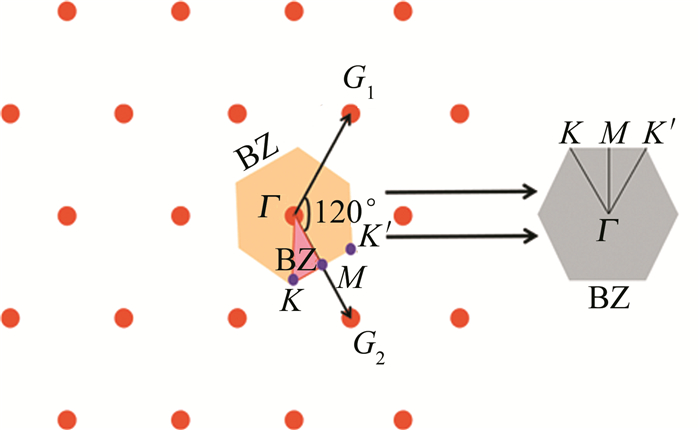
如图 2所示,是三角晶格原胞结构,在倒格矢空间相对应的布里渊区(Brillouin zone,BZ)如图 3所示,Γ-M-K-Γ所围成的区域作为不可约布里渊区。
3. 仿真与分析
3.1 直径调节与能带拓扑效应
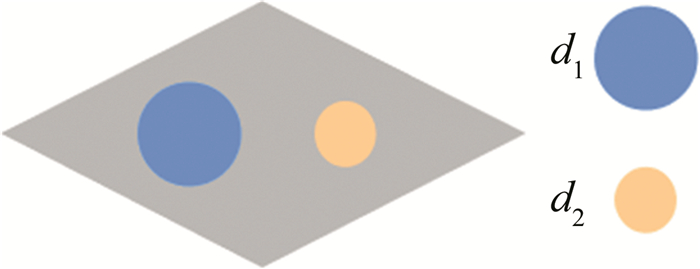
对石墨烯等离激元光子晶体结构的研究中发现,石墨烯圆盘的大小可打开狄拉克点,对带隙进行改变,可实现能带拓扑效应。本小节中将研究直径调节与能带拓扑效应的关系,将菱形晶格中的两个石墨烯圆盘直径分别设置为d1(左)和d2(右),如图 4所示。
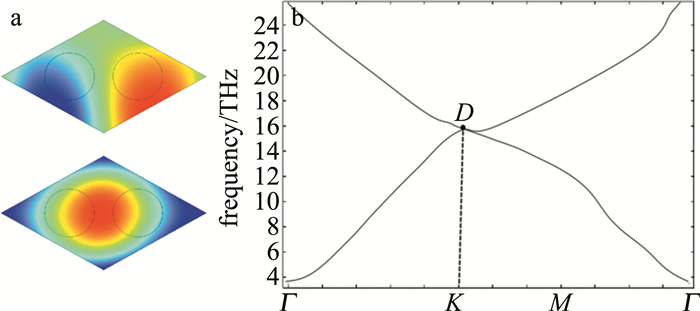
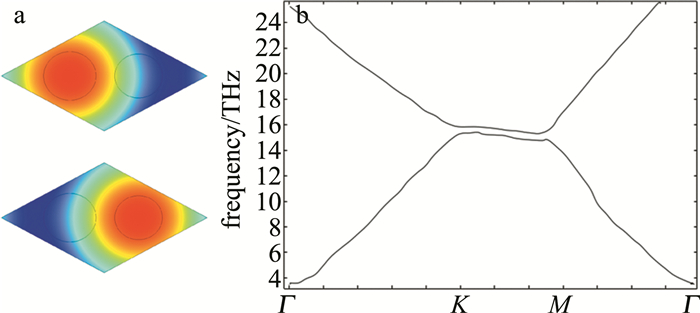
将背景基底的石墨烯等离激元的化学势μ3设置为0.62eV,同一周期内的两个石墨烯圆盘化学势保持一致,设置μ1=μ2=0.4eV,即δμ=0,避免化学势差值对仿真结果的影响,其中,μ1和μ2分别是以d1和d2为直径的石墨烯圆盘化学势。当d1=d2=0.42a,即δd=0时,仿真分析得其光场分布与能带结构如图 5所示。
如图 5b所示,能带图中不存在带隙,但在布里渊区角点K/K′相交形成的锥形色散,即狄拉克锥; D点为二重简并点,被称作狄拉克点。
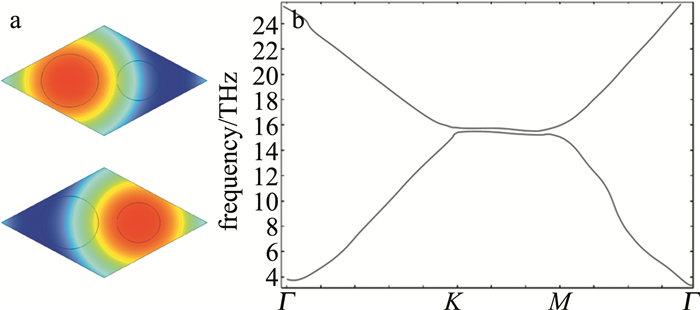
当两石墨烯圆盘直径d1=0.4a,d2=0.44a时,仿真结果如图 6所示。狄拉克点被成功打开,在15.3THz~15.8THz频率范围内,获得间隙为0.5THz的带隙。
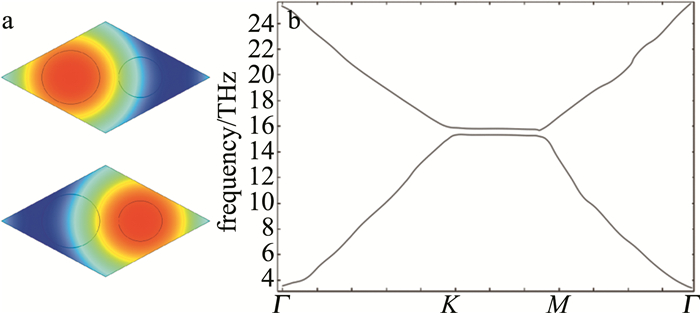
当两石墨烯圆盘直径d1=0.38a,d2=0.46a时,仿真结果如图 7所示。可见狄拉克点可仍被成功打开,在15.3THz~15.77THz频率范围内,获得间隙为0.47THz的带隙。
当两石墨烯圆盘直径d1=0.36a,d2=0.48a时,仿真结果如图 8所示。可见狄拉克点仍被成功打开,在15.3THz~15.75THz频率范围内,获得间隙为0.45THz的带隙。
此后还分别模拟分析d1=0.34a,d2=0.5a和d1=0.52a,d2=0.32a时的光场分布和能带结构,狄拉克点都可被成功打开,并分别获得了0.4THz与0.38THz的带隙。
3.2 动态可调谐分析
在第3.1节的研究分析中,基于周期内石墨烯圆盘相同化学势的状态下,通过调节其石墨烯两圆盘的大小能打开狄拉克点,实现能带拓扑效应,同时得到不同频率范围的带隙。
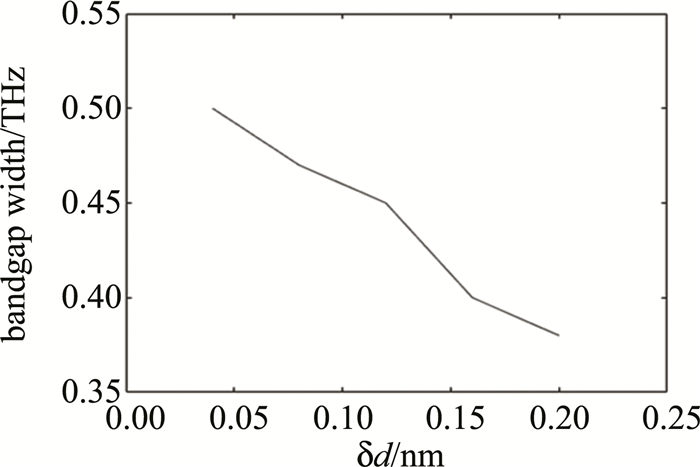
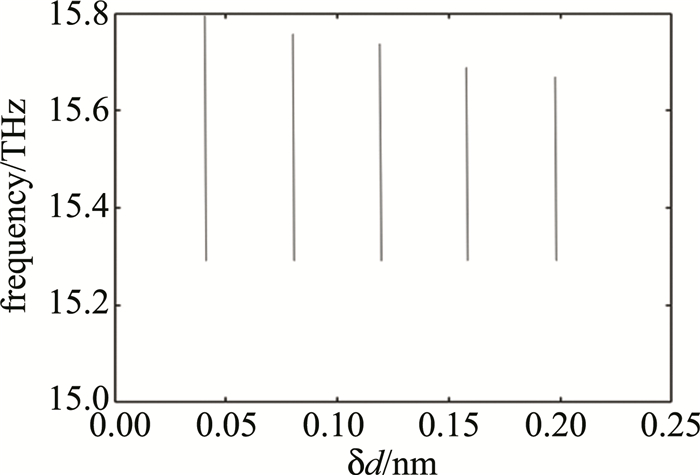
当直径差值δd分别于0.04a,0.08a,0.12a,0.16a,0.2a动态变化时,分别打开了位于15.3THz~15.8THz,15.3THz~15.77THz,15.3THz~15.75THz,15.3THz~15.7THz,15.5THz~15.688THz范围内的带隙。基于上述研究,对带隙范围和间隙大小的数据进行统计分析。
由图 9和图 10可见,当一个周期内的两个石墨烯圆盘的直径大小差值逐渐增加时,带隙频率范围逐渐下移,通过直径差值于0.04a~0.2a间以步长为0.04a进行调节,在频率范围15.3THz~15.8THz间实现可调谐。随着圆盘大小差值增大,获得带隙宽度逐渐变窄。
实验表明,通过调节石墨烯圆盘的直径,可在保持化学势不变的状态下,实现石墨烯拓扑光电子器件在15.3THz~15.8THz频段的工作范围。
4. 结论
拓扑效应革新了光子晶体中传统光学传输的认知,在光子学领域具有巨大潜力。本文中提出一种新型石墨烯的等离激元光子晶体表面结构,基于石墨烯圆盘直径大小的调节,实现在15.3THz~15.8THz频段内动态调制,具有工作的灵活性。理论计算分析表明,相较于普通的拓扑光子器件,引入了石墨烯后,可有效提高光传播性能;晶格常数及模式体积均降至纳米量级,比自由空间波长小了近30倍,为纳米量级的高集成度光电子传输器件的设计提供全新而有价值的理论依据。
作者下一步将在本文中提出的结构基础上,设想一种拓扑边界传输通道的方案。为更大程度地实现器件的灵活性和可重构性,通过调节以图 1菱形为周期的两个石墨烯圆盘的直径大小,于两个石墨烯圆盘中间的结构表面构建通道,局域特定频段的电磁波,实现拓扑边界传输。
关于动态控制的工作方式,提出控制通断的光开关功能:基于上述提出的通道,研究石墨烯圆盘的直径差值,设计实现通道打开的枢纽:当一个周期内两个石墨烯圆盘的面积存在差值时,该通道为导通状态;当直径差值恢复为0时,通道关闭。
-
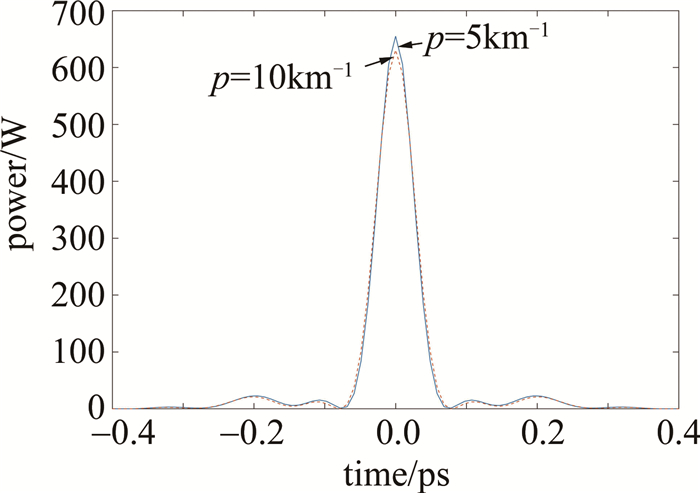
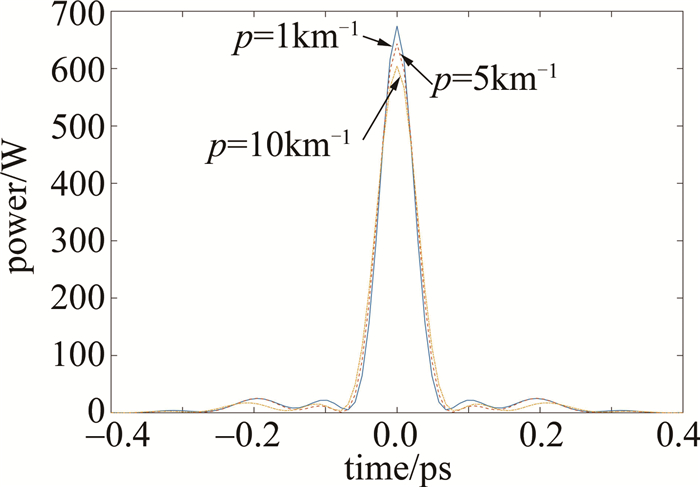
Table 1 Numerical simulation results of fibers with linearly increasing dispersion
p=1km-1 p=5km-1 p=10km-1 optimal compensation fiber length/m 93.0 81.0 74.2 full width at half maximum of ultrashort pulse output/fs 53.8 58.0 61.8 peak power of output pulse/W 688.2 655.1 630.6 Table 2 Numerical simulation results of fibers with increasing dispersion index
p=1km-1 p=5km-1 p=10km-1 optimal compensation fiber length/m 92.5 82.5 70.3 full width at half maximum of ultrashort pulse output/fs 54.2 59.4 64.4 peak power of output pulse/W 674.2 643.3 604.4 -
[1] FERMANN M E, KRUGLOV V I, THOMSEN B C, et al. Self-similar propagation and amplification of parabolic pulses in optical fibers[J]. Physical Review Letters, 2000, 84(26): 156-159. http://europepmc.org/abstract/med/10991111
[2] QIAO F Zh, JIAN G. Generation of excellent self-similar pulses in a dispersion-decreasing fiber[J]. Optik—International Journal for Light and Electron Optics, 2010, 122(19): 256-259.
[3] QIAO F Zh, YAO H D. Influence of gain coefficient on the self-similar pulses propagation in a dispersion-decreasing fiber[J]. Optik—International Journal for Light and Electron Optics, 2016, 127(12): 98-104. http://www.sciencedirect.com/science/article/pii/S0030402616301358
[4] SHI Sh D, ZHANG Q F, WU L M. Analysis of transmission characteristics of pulses in super-Gaussian dispersion-decreasing fibers[J]. Laser Technology, 2020, 44(3): 388-392(in Chinese).
[5] XU K, YANG O. Theoretical and numerical characterization of a 40 Gbps long-haul multi-channel transmission system with dispersion compensation[J]. Digital Communication Networds, 2015, 1(3): 222-228. DOI: 10.1016/j.dcan.2015.06.001
[6] RAJNEESH K, KALER R. Comparison of dispersion mapping techniques with fiber nonlinearities in carrier suppressed RZ system[J]. Optik, 2014, 4(7): 1416-1421. http://www.sciencedirect.com/science/article/pii/S0030402609001016
[7] WANG K, YU J, YU L Y. Research on dispersion compensation with chirped fiber grating[J]. Journal of Zhejiang University of Technology, 2008, 36(1): 77-80(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-ZJGD200801019.htm
[8] LIU W, SCHIMPF D N, EIDAM T, et al. Pre-chirp managed nonlinear amplification in fibers delivering 100W, 60fs pulses[J]. Optics Letters, 2015, 40(2): 203-205. http://www.opticsinfobase.org/abstract.cfm?URI=ol-40-2-151
[9] BOSCOLO S, TURITSYN S K, NOVOKSHENOV Y V, et al. Self-similar parabolic optical solitary waves[J]. Theoretical and Mathematical Physics, 2002, 133(3): 320-324. http://www.springerlink.com/content/p84p80qq6j787w16/
[10] LIMPERT J, SCHREIBER T, ZÖLLNER K, et al. High-power femtosecond Yb-doped fiber amplifier[J]. Optics Express, 2002, 10(14): 628-631. DOI: 10.1364/OE.10.000628
[11] ZOU Y Q, MA J Sh. Simulation of different compensation method of the dispersion compensation fiber[J]. Optical Instruments, 2012, 34(5): 11-16(in Chinese). http://en.cnki.com.cn/Article_en/CJFDTOTAL-GXYQ201205003.htm
[12] WU Q, YU Ch X, XIN Y, et al. Analysis on dispersion compensation with DCF[J]. Semiconductor Optoelectronics, 2003, 24(3): 186-188(in Chinese). http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5565685
[13] LONG X. Research on dispersion compensation technology and development in fiber-optic system[J]. Optical Communication Technology, 2009, 33(10): 58-59(in Chinese).
-
期刊类型引用(1)
1. 郜洋,吴智杭,余明芯,罗浩翔,张克非. 测量多种气体体积分数的PCF传感器结构. 应用激光. 2024(02): 86-93 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: