-
激光具有单色性好、色域宽、亮度高、寿命长等众多优点,使得激光作为显示技术的光源具有更大的显示色域、更高的图像对比度、画面色彩更加鲜艳的优势[1-8]。然而其高度的相干性使得激光作为光源所形成的画面具有颗粒状、不均匀强度分布的散斑,这一特点降低了图像的清晰度,长时间观看满是散斑的图像也会导致人眼疲劳[9-10]。
在投影成像系统中,作为图像散斑评价标准的主要参数是衬比度大小,其定义为散斑光强的标准偏差与散斑光强的平均值之比[11]。衬比度可作为散斑现象的度量,当散斑现象严重时,衬比度值大;反之衬比度趋于零[12]。据研究表明,人眼感受不到衬比度低于4%的散斑[13]。目前,国内外对激光散斑抑制的研究大都是基于叠加统计独立散斑图样,通过在光强上实现时间或空间积分来达到抑制散斑的目的,如振动光纤,可将散斑衬比度降到3%左右[14-17];或旋转磨砂玻璃,可将散斑衬比度降低至1%[18];通过用超声波调制激光束来消除散斑,散斑衬比度降至3%[12]。然而,虽然这些方法均可将散斑衬比度降低到人眼无法识别的程度,但是这些测量结果均是通过激光非投影系统测量所得。在实际激光投影系统中,经过这些方法削弱的激光散斑,通过激光投影镜头后光场的空间相干性又会有所增加,从而导致散斑衬比度变大。
本文中基于激光投影系统,理论上分别分析了利用多模光纤及级联随机位相片抑制激光散斑时散斑衬比度的影响因素。在研究多模光纤法抑制激光散斑原理中,分析了独立散斑图样统计的数量M和投影屏幕上处于一个眼睛分辨基元内的投影镜头分辨基元的数量K对散斑衬比度的影响。M由光纤传输特性决定,与时间积分散斑相关,称为系统的时间自由度数;K由投影系统参数决定,与空间积分散斑相关,称为系统的空间自由度数。基于散斑统计理论,建立了光纤长度与光纤末端出射光场衬比度的数值表达式,并实验研究了光纤长度对光纤末端出射光场衬比度的影响。在级联随机位相片抑制激光散斑研究中,分析了级联位相片散射特性和运动特性对散斑衬比度的影响, 并通过系统实验,研究了不同光纤长度下振动光纤前后图像的散斑衬比度,比较了运用振动多模光纤单种散斑抑制机制和运用光纤振动与旋转级联位相片结合复合散斑机制所获得的散斑图像衬比度。
-
多模光纤中由于存在多模色散,不同模式的光线由于传输角度不同,在光纤中传播距离也不同,导致它们在光纤中有不同的相位延迟,使得光纤出射端光场相干性减弱。此外,光纤中各个模式的相速度对环境温度、压力及光纤的运动变化非常敏感,均会引起光纤末端端面出射光场的改变。当光纤末端端面出射光场作为投影仪的照明光源时,不同光纤模式对应不同的时间(位相)延迟,相当于通过了一个随机位相片调制。GOODMAN分析了光学投影显示中用变化的漫射体抑制散斑时,当漫射体不溢出投影镜头情况下,投影图像的散斑衬比度为[11]:
$ C=\sqrt{\frac{M+K-1}{M K}} $
(1) 式中: M是在人眼分辨时间内由于漫射体快速移动而产生的独立统计的强度模式的数量; K是投影屏幕上处于一个眼睛分辨基元内包含的投影镜头分辨基元的数量。
当漫射体溢出投影镜头情况下,则投影图像的散斑衬比度为[11]:
$ C=\sqrt{\frac{M+K+1}{M K}} $
(2) 当投影镜头是出瞳直径为D的圆,且到屏幕的距离为z1,而探测系统是通光孔径为P的圆,且距离屏幕距离为z2时,K可表示为[19]:
$ \begin{equation*} K \approx\left(\frac{z_{2} D}{z_{1} P}\right)^{2}=\left(\frac{d_{\mathrm{NA}, \mathrm{p}}}{d_{\mathrm{NA}, \mathrm{d}}}\right)^{2} \end{equation*} $
(3) 式中: dNA, p是从屏幕上看投影镜头的数值孔径; dNA, d是从屏幕上看成像透镜的数值孔径。
对于多模阶跃折射率光纤支持的传输模式数量为[11]:
$ M_{\mathrm{t}} \approx \frac{2 {\rm{ \mathsf{ π}}}}{\lambda_{0}}\left(d_{\mathrm{NA}}\right) a $
(4) 式中: a为纤芯半径; λ0是光在空气中的波长; dNA是光纤数值孔径。对于阶跃光纤而言,在光纤出射端面上散斑相关的元胞数量约等于光纤中传输的模式数量[20],即M=Mt。
在光纤法抑制散斑的投影光学系统中,M和K通常远大于1,式(1)、式(2)可近似为:
$ C \approx \sqrt{\frac{1}{M}+\frac{1}{K}} $
(5) 由式(5)可见, 所观测到的散斑衬比度影响不仅取决于光纤末端光场特性,亦取决于投影光学系统特性。即使当来自光纤末端低对比度光照射时(此时对应M值很大),通过投影仪的投影镜头后光场的空间相干性也会有所增加,从而导致散斑衬比度变大。
所以,为达到减少观测到的散斑衬比度,可增大时间自由度数M。例如,当光纤受到振动,光纤中的各个传播模式受到的相位延迟也发生改变,从而导致光纤末端端面上产生了更多的散斑相关元胞数,即时间自由度数M增大。当M值达到一定大小后, 散斑衬比度取决于K,即此时散斑衬比度受限于投影系统空间自由度。另外, 减弱散斑衬比度的方法就是增加投影系统的空间自由度数K,通常方法是增加投影光学系统镜头的数值孔径来达到,但是该方案是以减弱观测到的图像分辨率或是增大投影镜头的衍射效应为代价的。
下面讨论多模光纤末端散斑特性的影响因素。参考文献[20]中给出了理想情况下,光谱分布为高斯型时多模光纤输出端的散斑衬比度为:
$ \left\{\begin{array}{l} C(L)^{2}=\left[1+\frac{1}{2}(2 {\rm{ \mathsf{ π}}} \Delta \nu)^{ 2} T_{\mathrm{g}}{ }^{\prime 2}\right]^{-\frac{1}{2}} \\ |\Delta \nu|=\frac{c}{\lambda^{2}} \Delta \lambda \\ T_{\mathrm{g}}{ }^{\prime}=\frac{\Delta \tau}{\sqrt{3}} \end{array}\right. $
(6) 式中: L为光纤长度; λ为高斯光谱中心波长; Δλ为高斯单线线宽; Δν为高斯单线频谱宽度; Tg′为平均延迟时间; Δτ为光纤中最快模式和最慢模式之间的时间延迟,满足:
$ \Delta \tau=\frac{d_{\mathrm{NA}}{ }^{2} L}{2 n_{1} c} $
(7) 式中:n1为光纤纤芯折射率,c为真空中的光速。式(7)适用于光纤长度L比光纤模式耦合长度Lc短得多的情况。实际应用中为了减少传播过程中的损耗,通常选用的光纤长度也是远小于光纤模式耦合长度。
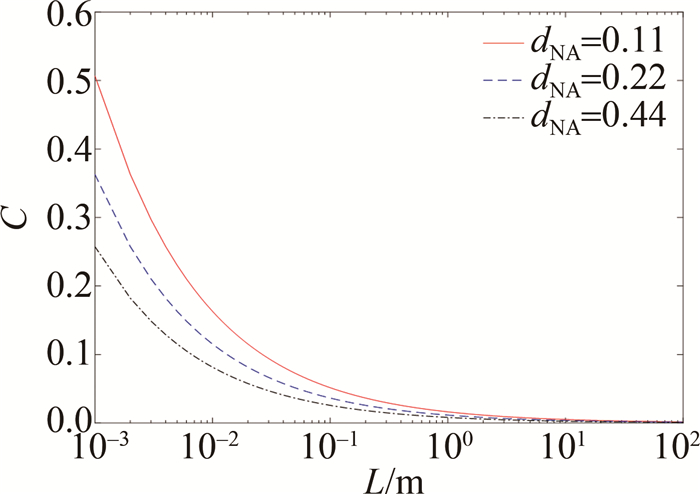
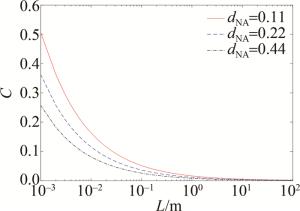
取高斯光谱中心波长λ=500 nm、单线线宽Δλ=0.1 nm、阶跃光纤纤芯折射率n1=1.5时,散斑衬比度C与光纤长度L关系满足图 1。图中红色实线是光纤数值孔径为0.11,蓝色虚线是光纤数值孔径为0.22,黑色点划线是光纤数值孔径为0.44。从图中可见, 散斑衬比度随着光纤长度的加大而减小,当光纤长度L>10 m之后,光纤长度的增加使得散斑衬比度的减小不显著。
-
基于旋转随机位相片动态调制照射光束形成散斑图样多样性是目前较为有效和实用的散斑抑制技术方法之一。该方法是利用人眼的视觉暂留效应,由随机位相片改变激光光源散射的角度,使得激光投影产生的散斑图样在屏幕上随时间快速变化,在人眼积分时间内散斑图样快速非相干叠加,人眼观察到的屏幕散斑就大大减弱,可用下式表示:
$ I_{\text {total }}\left(\lambda_{i}\right) \propto \int_{0}^{T} V\left(\lambda_{i}\right) I(t) \mathrm{d} t $
(8) 式中: Itotal(λi)表示波长为λi的总光强; T为人眼积分时间; I(t)为t时刻散射光在人眼中干涉产生的散斑的光强; V(λi)是波长为λi光的视觉响应函数。
对于单色性极好的激光光源而言,仅通过单个运动位相片来降低激光的相干性存在一定的局限性,这使得对散斑的抑制效果不够理想。因此,在运动位相片后加入固定位相片,以便获得更高的位相调制效果,达到更佳的散斑抑制,如图 2所示。

图 2 由级联位相片抑制激光散斑的示意图
Figure 2. Schematic diagram of experimental system for suppressing laser speckle by cascade diffusers
在此模型中,为分析方便假设两位相片所在平面均用(α, β)表示,屏幕所在平面用(x, y)表示,且两个位相片的透射率均为1,投影系统的点扩展函数为h(x, y; α, β),入射到运动位相片上的光场为a0(α, β),从固定位相片出射的光场分布可表示为:
$ \begin{gather*} a(\alpha, \beta, t)=a_{0}(\alpha, \beta) \tau_{1}(\alpha, \beta, t) \tau_{2}(\alpha, \beta)= \\ a_{0}(\alpha, \beta) \exp \left[\mathrm{j} \varphi_{0}(\alpha, \beta)\right] \exp \left[\mathrm{j} \varphi_{\mathrm{d}}(\alpha+v t, \beta)\right] \end{gather*} $
(9) 式中: τ1(α, β, t)和τ2(α, β)分别为运动位相片及固定位相片的透射函数; φo(·)是固定位相片贡献的相位; φd(·)是运动位相片贡献的相位; v为运动位相片的运动速度。
则屏幕上的光场为:
$ A(x, y, t)=\iint h(x, y ; \alpha, \beta) a(\alpha, \beta, t) \mathrm{d} \alpha \mathrm{d} \beta $
(10) 如投影系统光曈函数为P(ξ, η),(ξ, η)表示光曈所在平面,那么点扩展函数h(x, y; α, β)可由下式给出:
$ \begin{gather*} h(x, y ; \alpha, \beta)=\frac{1}{\lambda^{2} z^{2}} \exp \left[\mathrm{j} \frac{{\rm{ \mathsf{ π}}}}{\lambda z^{2}}\left(\alpha^{2}+\beta^{2}\right)\right] \times \\ \iint_{-\infty}^{\infty} P(\xi, \eta) \exp \left\{-\mathrm{j} \frac{{\rm{ \mathsf{ π}}}}{\lambda z^{2}}[\xi(\alpha+x)+\right. \\ \eta(\beta+y)]\} \mathrm{d} \xi \mathrm{d} \eta \end{gather*} $
(11) 式中: λ为入射光谱中心波长; z为投影系统到屏幕的距离。
运动位相片运动前后屏幕上两个光场的时间自相关函数为:
$ \begin{gather*} \varGamma_{A}(\Delta t)=\left\langle A(0, 0 ; t) A^{*}(0, 0 ; t+\Delta t)\right\rangle= \\ \iint_{\infty} \iint_{\infty} h\left(\alpha_{1}, \beta_{1}\right) h^{*}\left(\alpha_{2}, \beta_{2}\right) \times \\ \left\langle a\left(\alpha_{1}, \beta_{1} ; t\right) a^{*}\left(\alpha_{2}, \beta_{2} ; t+\Delta t\right)\right\rangle \mathrm{d} \alpha_{1} \mathrm{~d} \beta_{1} \mathrm{~d} \alpha_{2} \mathrm{~d} \beta_{2} \end{gather*} $
(12) 式中: Δt为位相片运动时间; *表示对应函数的复数共轭。其中:
$ \begin{array}{c} \left\langle a\left(\alpha_{1}, \beta_{1} ; t\right) a^{*}\left(\alpha_{2}, \beta_{2} ; t+\Delta t\right)\right\rangle=\\ \left|a_{0}\right|^{2} \exp \left\{\left\langle\mathrm{j}\left[\varphi_{0}\left(\alpha_{1}, \beta_{1}\right)-\varphi_{0}\left(\alpha_{2}, \beta_{2}\right)\right]\right\rangle\right\} \times\\ \exp \left\{\left\langle\mathrm{j}\left[\varphi_{\mathrm{d}}\left(\alpha_{1}+v t, \beta_{1}\right)-\varphi_{\mathrm{d}}\left(\alpha_{2}+v t+v \Delta t, \beta_{2}\right)\right]\right\rangle\right\}=\\ \left|a_{0}\right|^{2} \exp \left\{-{\sigma_{{\rm{o}}}}^{2}\left[1-\mu_{\mathrm{o}}(\Delta \alpha, \Delta \beta)\right]\right\} \times \\ \exp \left\{-{\sigma_{\mathrm{d}}}^{2}\left[1-\mu_{\mathrm{d}}(\Delta \alpha+v t, \Delta \beta)\right]\right\} \end{array} $
(13) 为分析方便, 假设入射位相片上光场振幅均匀, 即a0(α, β)=a0; 运动位相片的运动位移Δα=α1-α2和Δβ=β1-β2; σo2是φo(·)的方差; σd2是φd(·)的方差; μo(·)和μd(·)是两个相位的归一化自相关函数,于是光场的时间自相关函数式(12)可以化为:
$ \begin{gather*} \varGamma_{A}(\Delta t)=\left|a_{0}\right|^{2} \iint_{\infty} H(\Delta \alpha, \Delta \beta) \times \\ \exp \left\{-{\sigma_{\mathrm{o}}}^{2}\left[1-\mu_{\mathrm{o}}(\Delta \alpha, \Delta \beta)\right]\right\} \times \\ \exp \left\{-{\sigma_{\mathrm{d}}}^{2}\left[1-\mu_{\mathrm{d}}(\Delta \alpha+v t, \Delta \beta)\right]\right\} \mathrm{d} \Delta \alpha \mathrm{d} \Delta \beta \end{gather*} $
(14) 其中,
$ \begin{gather*} H(\Delta \alpha, \Delta \beta)= \\ \iint_{\infty} h\left(\alpha_{1}, \beta_{1}\right) h^{*}\left(\alpha_{1}-\Delta \alpha, \beta_{1}-\Delta \beta\right) \mathrm{d} \alpha_{1} \mathrm{~d} \beta_{1}= \\ \frac{{\rm{ \mathsf{ π}}} D^{2}}{(\lambda z)^{2}}\left[2 \frac{\mathrm{J}_{1}\left(\frac{{\rm{ \mathsf{ π}}} D \sqrt{\Delta \alpha^{2}+\Delta \beta^{2}}}{\lambda z}\right)}{\frac{{\rm{ \mathsf{ π}}} D \sqrt{\Delta \alpha^{2}+\Delta \beta^{2}}}{\lambda z}}\right] \end{gather*} $
(15) 式中: D为投影镜头通光孔径; J1(·)是1阶的第1类Bessel函数。
归一化处理后得光场A的归一化强度自协方差函数:
$ \begin{gather*} \mu_{A}(\Delta t) \approx \frac{H(\Delta \alpha, \Delta \beta)}{H(0, 0)}= \\ 2 \frac{\mathrm{J}_{1}\left(\frac{{\rm{ \mathsf{ π}}} D \sqrt{\Delta \alpha^{2}+\Delta \beta^{2}}}{\lambda z}\right)}{\frac{{\rm{ \mathsf{ π}}} D \sqrt{\Delta \alpha^{2}+\Delta \beta^{2}}}{\lambda z}} \end{gather*} $
(16) 根据Goodman的积分散斑统计学理论,屏幕上时间自由度数N为[11]:
$ \begin{equation*} N \approx\left[\frac{2}{T} \int_{0}^{T}\left(1-\frac{\Delta t}{T}\right)\left|\mu_{A}(\Delta t)\right|^{2} \mathrm{~d} \Delta t\right]^{-1} \end{equation*} $
(17) 式中: T表示人眼积分时间; 自由度数目N表示在该运动装置下T时间内产生的独立散斑图像个数。可以得到这种情况下散斑图像衬比度为:
$ \begin{equation*} C=\sqrt{\frac{1}{N}}=\sqrt{\frac{2}{T} \int_{0}^{T}\left(1-\frac{\Delta t}{T}\right)\left|\mu_{A}(\Delta t)\right|^{2} \mathrm{~d} \Delta t} \end{equation*} $
(18) 将式(16)代入式(18)中, 即可获得级联位相片散射特性和运动特性对散斑衬比度的影响。
-
根据Goodman理论,每一种散斑抑制方法均会为系统增加一定数量的自由度[11],如采用上述振动多模光纤法和级联随机位相片两种独立机制均可为投影系统提供自由度,设自由度的总数为SDOF,其与前述参数振动光纤引入的时间自由度数M、投影光学系统的空间自由度数K、级联位相片散射特性和运动特性引入的自由度数目N相关,系统自由度总数SDOF可表示为:
$ S_{\mathrm{DOF}}=f(M, K, N) $
(19) 则复合散斑抑制技术所得到的散斑总的衬比度为:
$ C=\frac{1}{\sqrt{S_{\mathrm{DOF}}}} $
(20) 由此可见,如在投影系统中采用复合散斑抑制技术可在一定程度上增加系统自由度,达到降低散斑衬比度的目的,但这是以增加系统复杂度为代价的。实际中应综合考虑系统在满足实际结构需求的前提下尝试采用尽可能合适的复合散斑抑制方法,达到最大量的散斑总体抑制。
-
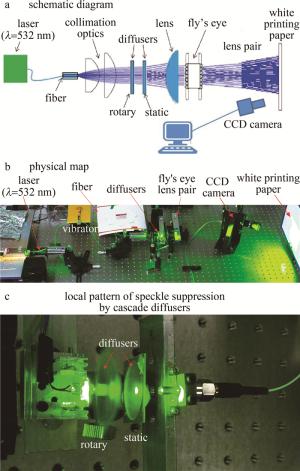
光纤法抑制散斑衬比度实验装置如图 3所示。光源采用掺氧化镁周期极化铌酸锂(periodically-poled MgO doped lithium niobate,PPMgOLN)晶体内腔倍频532 nm光胶微片绿光激光器,激光器发出的光通过短焦距透镜耦合进以1 kHz频率点击振动的多模阶跃光纤中,后经透镜组准直和扩束,最后经复眼整型透镜匀光整型后投射在白屏上。距离投影屏幕3 m的正前方固定CCD相机用于拍摄白屏上的散斑图像,CCD曝光时间设置为20 ms,孔径被设置为3 mm(这个宽度是人眼在明亮区域的瞳孔直径),调节镜头F数到2.5左右。之后对CCD采集的原图像文件转换为无损压缩的BMP格式,在计算机中调用BMP图像文件,并将每幅图像格式化的滤除暗区,然后统一选取图像大小为256×256,通过相关软件将彩色图像转化为灰度图像,并读取图像像素点的灰度值,计算得出投影图片散斑衬比度。
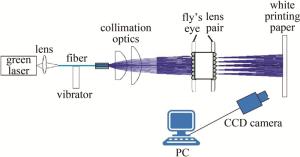
图 3 光纤法抑制散斑衬比度实验装置图
Figure 3. Experimental setup of speckle contrast inhibition by optical fiber method
实验中选取芯径大小为105 μm、耦合长度约为500 m的多模光纤,分别取长度为0.7 m、1 m、2 m、7 m和10 m 5种不同光纤长度状态下振动光纤前后所得散斑图像的衬比度, 如表 1所示。从实验结果可见, 未振动光纤时,随着光纤长度的增加,散斑图像衬比度逐渐降低,这点与前述仿真结果(见图 1)变化趋势一致。从图 1中可知, 在光纤长度增大到10 m之后,增加光纤长度对减小散斑衬比度贡献不大; 从表 1中发现,在光纤长度增加到10 m长时所获得的图像衬比度尚未降低到人眼未能分辨程度0.04。加入振动机制后,相对于在探测器探测时间内增加了独立散斑个数,即在光纤末端端面上产生了更多的散斑相关元胞数,增加了时间自由度数M,则越有利于激光散斑的抑制。由表 1中的实验结果可见,加入振动机制后相同长度光纤条件下获得的散斑衬比度更低。然而振动10 m光纤所获得散斑图像衬比度虽已达到最小0.0469,但是仍未达到人眼未能分辨的程度。
表 1 不同光纤长度时散斑衬比度实验情况
Table 1. Measured speckle contrasts for different fiber lengths
fiber length/m 0.7 1 2 7 10 speckle contrast C of static 0.0772 0.0773 0.0683 0.0570 0.0537 speckle contrast C of moving 0.0582 0.0550 0.0529 0.0479 0.0469 -
利用多模光纤(长度10 m)振动与旋转级联位相片结合的方法抑制散斑,实验装置如图 4所示。光源采用波长为532 nm半导体带尾纤的激光器,激光耦合进以1 kHz频率点击振动的多模阶跃光纤中,后经透镜组准直和扩束,以平行光入射到两片级联随机相位片上,一片相位片旋转运动(发散角:10°;透过率:90% @532 nm),一片相位片静止(发散角:5°;透过率:93% @532 nm)。光束最后经复眼整型透镜匀光整型后投射在白屏上。采用与光纤法抑制激光散斑实验中相同的测量条件进行散斑图像采集与衬比度计算。
图 5a显示了原始散斑图像和对应散斑图中各像素点的灰度级分布图;图 5b是加入10 m光纤散斑抑制方法时所获得的散斑图像及各像素点灰度级分布图,此时测得散斑图像衬比度为0.0537;当同时加入10 m光纤振动和旋转级联位相片两种散斑抑制方法时,测得散斑图像衬比度为0.0376,如图 5c所示。灰度级分布图中各像素的灰度等级(gray-level)反映出原散斑图中光强I的分布。从图中可以看出,在相同检测条件下,加入多种抑制散斑抑制技术可以更加有效地降低图像的散斑衬比度,改善投影图像的成像质量。可见,同时采用多种抑制散斑方法可达到最大量的散斑总体抑制,实验结果与理论分析相吻合。
-
基于散斑统计理论,分析了激光投影显示系统中采用振动多模光纤抑制激光散斑时影响散斑衬比度的两个关键参数,即光通过多模光纤的平均时间延迟内所包含的独立光纤模式数(时间自由度数M)和投影屏幕上处于一个眼睛分辨基元内的投影镜头分辨基元的数量(空间自由度数K)。无论是M还是K的增大,都将有效降低图像散斑,但即使时间自由度数M很大,此时散斑衬比度仍受限于投影系统空间自由度数K。在投影系统中运用光纤振动方法后再加入旋转级联相位片方法调试时,将引入新的系统自由度数目N,进一步降低散斑衬比度。通过系统实验,研究了不同光纤长度下振动光纤前后图像的散斑衬比度,比较了运用散斑抑制技术和光纤振动与旋转级联位相片结合的复合散斑抑制技术所获得的散斑图像衬比度。实验结果表明,在光纤长度小于模式耦合长度情况下,通过增加光纤长度、振动光纤并引入旋转级联位相片多种散斑抑制机制的复合散斑抑制技术,可增加投影系统自由度数目,更有利于散斑的抑制。该研究为激光投影显示中开展复合散斑抑制技术提供了参考。
激光投影显示中复合散斑抑制方法的研究
Analysis of composite speckle suppression technique in laser projection display
-
摘要: 为了有效抑制激光投影显示中的散斑, 基于散斑统计理论, 建立了光纤长度与光纤末端出射光场衬比度的数值表达式; 采用积分散斑统计学方法理论分析了级联位相片散射特性和运动特性对散斑衬比度的影响; 实验研究了不同光纤长度下振动光纤前后图像的散斑衬比度; 比较了运用散斑抑制技术和复合散斑抑制技术所获得的散斑图像衬比度。结果表明, 采用振动10 m多模光纤与旋转级联位相片相结合的复合散斑抑制技术, 可将散斑衬比度降低到3.76%;采用复合散斑抑制技术将增加系统自由度, 从而更有效地抑制散斑。该研究为激光投影显示中开展复合散斑抑制技术研究工作提供了参考。Abstract: In order to effectively suppress speckles in laser projection display, a numerical expression of the optical fiber length and the optical field contrast degree at the end of the optical fiber was established based on speckle statistical theory. Based on the integral scattering statistics method, the effect of scattering and moving properties of the multiple scatter diffuser on speckle contrast was analyzed. The experimental results show that the laser speckle contrast ratio can reduce 3.76% by using the composite speckle suppression technology combining a vibrating 10 m multimode fiber with a rotating cascade diffuser. Using composite speckle suppression technique can increase the system's freedom, which contributes to speckle suppression. This study can provide a reference for the research work of composite speckle suppression technique in laser projection display.
-
表 1 不同光纤长度时散斑衬比度实验情况
Table 1. Measured speckle contrasts for different fiber lengths
fiber length/m 0.7 1 2 7 10 speckle contrast C of static 0.0772 0.0773 0.0683 0.0570 0.0537 speckle contrast C of moving 0.0582 0.0550 0.0529 0.0479 0.0469 -
[1] 孙敏远, 朱建英, 毕勇, 等. 激光显示中颜色配比与实时色温控制研究[J]. 中国激光, 2020, 47(7): 0704001. SUN M Y, ZHU J Y, BI Y, et al. Color matching and real-time color temperature control in laser display[J]. Chinese Journal of Lasers, 2020, 47(7): 0704001(in Chinese). [2] 王飞霞, 金岑芩, 李晓华, 等. 激光投影电视的感知亮度与色度关系[J]. 光学学报, 2020, 40(13): 1333001. WANG F X, JIN C Q, LI X H, et al. Relationship between perceived brightness and chromaticity of laser projection television[J]. Acta Optica Sinica, 2020, 40(13): 1333001(in Chinese). [3] 孟雪, 宁永强, 张建伟, 等. 面向激光显示的红光半导体激光器的研究进展[J]. 激光与光电子学进展, 2019, 56(18): 180001. MENG X, NING Y Q, ZHANG J W, et al. Research progress of red semiconductor laser diodes for laser display[J]. Laser & Optoelectronics Progress, 2019, 56(18): 180001(in Chinese). [4] 薛亮, 黄茜. 激光技术在电力工程中的应用[J]. 上海电力学院学报, 2014, 30(4): 383-387. doi: 10.3969/j.issn.1006-4729.2014.04.019 XUE L, HUANG Q. Applications of laser technology in electric power[J]. Journal of Shanghai University of Electric Power, 2014, 30(4): 383-387(in Chinese). doi: 10.3969/j.issn.1006-4729.2014.04.019 [5] 刘敬伟. 激光投影显示散斑抑制方法研究[D]. 济南: 山东大学, 2015: 1-10. LIU J W. Research on speckle suppression in laser projection display[D]. Ji'nan: Shandong University, 2015: 1-10(in Chinese). [6] 赵新亮. 扫描式激光大屏幕显示技术研究[D]. 成都: 四川大学, 2005: 1-14. ZHAO X L. Study on large screen scanning laser display[D]. Chengdu: Sichuan University, 2005: 1-14(in Chinese). [7] ROELANDT S, MEURET Y, CRAGGS G, et al. Standardized speckle measurement method matched to human speckle perception in laser projection systems[J]. Optice Express, 2012, 20(8): 8770-8783. doi: 10.1364/OE.20.008770 [8] HUANG Q, DUAN X Y, HE Y W, et al. Optical lens designed for speckle measurement based on human eyes resolution cells on speckle pattern induced by laser projector[J]. Optics and Laser Technology, 2019, 112: 229-235. doi: 10.1016/j.optlastec.2018.11.025 [9] CONSIDINE P S. Effect of coherence on imaging systems[J]. Journal of the Optical Society of America, 1966, 56(8): 1001-1009. doi: 10.1364/JOSA.56.001001 [10] 安源, 姚建铨, 王鹏, 等. OCT图像散斑的形成机理和消除方法[J]. 光电子·激光, 2003, 14(3): 320-323. doi: 10.3321/j.issn:1005-0086.2003.03.026 AN Y, YAO J Q, WANG P, et al. The formation and elimination of speckles in optical coherence tomography[J]. Jouranl of Optoeclctronics·Laser, 2003, 14(3): 320-323(in Chinese). doi: 10.3321/j.issn:1005-0086.2003.03.026 [11] GOODMAN J W. 光学中的散斑现象-理论与应用[M]. 北京: 科学出版社, 2009. GOODMAN J W. Speckle phenomena in optics theory and applications[M]. Beijing: Science Press, 2009(in Chinese). [12] 钱亦蕾. 激光散斑衬比度成像中的噪声影响及修正方法[D]. 南京: 南京理工大学, 2016: 1-65. QIAN Y L. The effect of noise in laser scattering contrast imaging and correction methods[D]. Nanjing: Nanjing University of Science & Technology, 2016: 1-65(in Chinese). [13] WANG L L, TSCHUDI T, BOEDDINGHAUS M. et al. Speckle reduction in laser projections with ultrasonic waves[J]. Optical Engineering, 2000, 39(6): 1659-1664. doi: 10.1117/1.602543 [14] 王丽娟, 邱怡申, 陈怀熹, 等. 利用振动光纤减弱激光散斑的研究[J]. 光子学报, 2011, 40(8): 1211-1214. WANG L J, QIU Y Sh, CHEN H X, et al. Analysic of speckle reduction by the vibrating fiber[J]. Acta Photonica Sinica, 2011, 40(8): 1211-1214(in Chinese). [15] 王晓琳, 贺锋涛, 贾琼瑶, 等. 基于光纤振动的激光散斑控制[J]. 激光技术, 2014, 38(2): 177-180. WANG X L, HE F T, JIA Q Y, et al. Laser speckle control based on optical fiber vibration[J]. Laser Techonlogy, 2014, 38(2): 177-180(in Chinese). [16] 王静, 贺锋涛, 曹金凤, 等. 基于光纤振动的激光散斑抑制方法的研究[J]. 激光技术, 2015, 39(5): 666-668. WANG J, HE F T, CAO J F, et al. Research of laser speckle suppression method based on fiber vibration[J]. Laser Techonlogy, 2015, 39(5): 666-668(in Chinese). [17] 朱玉晗, 贺锋涛, 彭小龙. 基于塑料光纤的激光散斑特性研究[J]. 激光技术, 2016, 40(1): 122-125. ZHU Y H, HE F T, PENG X L. Research of characteristics of laser speckle of plastic optical fiber[J]. Laser Techonlogy, 2016, 40(1): 122-125(in Chinese). [18] VÖLKER A, ZAKHAROV P, WEBER B, et al. Laser speckle imaging with an active noise reduction scheme[J]. Optice Express, 2005, 13(24): 9782-9787. doi: 10.1364/OPEX.13.009782 [19] 黄艳. 激光投影成像中影响激光散斑抑制的参数分析及实验研究[J]. 激光与光电子学进展, 2022, 59(13): 1303001. HUANG Y. Parameter analysis and experimental study of influence on laser speckle suppression in laser projection imaging[J]. Laser & Optoelectronics Progress, 2022, 59(13): 1303001(in Chinese). [20] MANNI J G, GOODMAN J W. Versatile method for achieving 1% speckle contrast in large-venue laser projection displays using a stationary multimode optical fiber[J]. Optics Express, 2012, 20(10): 11288-11315. doi: 10.1364/OE.20.011288 -


 网站地图
网站地图

 下载:
下载: