-
奇异光学是现代光学的重要分支[1-2]。自1973年NYE等人提出波在传输过程中波前存在缺陷[3],光学中的奇异现象就引起了研究人员的兴趣。1992年,ALLEN及其同事基于拉盖尔-高斯光束提出了光的轨道角动量[4],引起了研究奇异光学的热潮。在奇异光学中,相位奇异是指标量光场相位为涡旋相位,表现为光场中存在强度为0的点,围绕该点的封闭路径的相位变化是2π的整数倍,该倍数即为拓扑荷。对于相位奇异,其拓扑荷通常为整数,但是也存在为非整数的情况。BERRY从理论上预测了分数涡旋相位的相位阶梯不连续将导致奇异线,并在其传播过程中会产生一系列复杂的演化[5]。LEACH等人在实验中观察到了该现象[6]。GBUR则发现这种复杂的演化与希尔伯特旅馆悖论密切相关[7]。XIONG等人利用连续镜面反射镜实现了对分数涡旋光束的动态调控[8]。
此外,对于矢量光场,存在着偏振奇异现象[9]。对于2维非均匀椭圆偏振光场,偏振奇异是指光场中无法定义其偏振方向的圆偏振点(C-points)或无法定义其偏振旋向的线偏振线(L-lines)。对于C点,其拓扑荷为±1/2。此外,还有光场中均为线偏振,但偏振方向成径向或旋向分布的柱矢量光束(V-points)和高阶偏振奇点。目前,偏振奇异光场可以由基于拉盖尔-高斯光束[10]、贝塞尔-高斯光束[11]、马修-高斯光束[12]、圆艾里光束[13]、分数涡旋光束[14]等新型光场得到。研究人员已经将偏振奇异应用于光学显微操作[15]、光学微加工[16]和光学通信等方面[17]。同时,偏振奇异还带来了很多有趣的物理现象,比如伪拓扑性[18]、奇点结19]、奇点爆炸[20]以及C点偶极子的产生与湮灭等[21]。对于V点,其拓扑荷通常为整数,然而ZHANG等人研究了V点拓扑荷为分数的情形,可以观察到偏振奇异线[22]。此后,他们又创造实现了Julia分数矢量光场,并验证了其伪拓扑性[18]。GU等人从理论和实验两方面研究了弱聚焦分数矢量光束的自旋角动量分离和传输特性[23]。
另一方面,无衍射光束因其独特的传输特性近些年来也越来越受到研究人员的关注,而其中艾里光束更是由于其加速性和自愈性吸引了大量的研究[24]。基于艾里光束,EFREMIDIS等人又提出了圆艾里光束[25],而后研究人员将其与涡旋相位结合,提出了艾里涡旋光束,并研究了其传播性质[26-28]。虽然C点的拓扑荷为分数,但是其通常基于整数拓扑荷的涡旋光束生成得到,对基于分数涡旋光束的偏振奇异光场虽已提出,但尚未研究其传输特性。本文中拟用携带分数涡旋相位的圆艾里光束来进行偏振奇异光场的传播特性研究。利用两束正交圆偏振的圆艾里光束的叠加,其中一束拓扑荷为0,另一束拓扑荷为分数,可以得到基于分数涡旋光束的偏振奇异光场,并且可以控制偏振奇异光场的拓扑荷并非传统的C点的±1/2,圆艾里光束的自聚焦特性会影响该光场在自由空间传播中的拓扑结构。本文中的研究展示了基于圆艾里光束的分数偏振奇点在传播过程中的拓扑结构演变,为其应用于自由空间光通信做好了理论基础,从而拓宽了圆艾里光束的应用场景。
-
为生成得到偏振奇异光场,采用了生成全庞加莱光束的方法[10],即叠加两束正交偏振的圆偏振光。位于初始平面z=0的叠加光场可以表示为[10]:
$ \boldsymbol{E}(\boldsymbol{r} ; \gamma)=\cos \gamma \cdot \boldsymbol{e}_1 U_1(\boldsymbol{r})+\sin \gamma \cdot \boldsymbol{e}_{\mathrm{r}} U_2(\boldsymbol{r}) $
(1) 式中: r为空间向量; γ为控制光束强度的常量参数; el和er分别为左旋和右旋圆偏振基矢量; U1(r)和U2(r)分别为携带或不携带涡旋相位的圆艾里光束。位于初始平面的携带涡旋相位的圆艾里光束,其电场在柱坐标系(r, φ, z)中可表示[26]:
$ \begin{aligned} U(r, \varphi, z=0)= & A_0 \cdot A\left(\frac{r_0-r}{w_0}\right) \exp \left(a \frac{r_0-r}{w_0}\right) \cdot \\ & {[r \exp (\mathrm{i} \varphi)]^l } \end{aligned} $
(2) 式中: A0为振幅常量; A(·)为艾里函数; r0为主艾里光环的半径; w0为径向缩放; a为决定传播距离的衰变参数; l为涡旋相位的拓扑荷。对于l=0,即代表圆艾里光束不携带涡旋相位。
为生成分数偏振奇异光场,将U1设置为携带涡旋相位且拓扑荷l为分数数值的圆艾里光束,U2为不携带涡旋相位的圆艾里光束。设定光场U1中l的数值为0.1、0.3、0.5、0.7、0.9和1.0,设定γ=π/4,r0=1 mm,w0=0.08 mm,a=0.1,光场尺寸为4 mm×4 mm。将上述参数结合式(1)和式(2),即U1为左旋圆偏振、U2为右旋圆偏振时,初始平面光场的偏振态分布如图 1所示。图中偏振椭圆的不同颜色代表了不同的旋向,绿色为右旋偏振,红色为左旋偏振。图 1展示了左旋分量U1中的拓扑荷不同时,光场偏振态分布的演化过程。当l=0.1时,光场偏振态接近于线偏振;随着l数值的不断变大,光场中偏振椭圆的椭圆率也随之变大;当l=1.0时,光场中出现了一个圆偏振点,即C点,此时光场的偏振态分布是一个典型的“柠檬”结构;当l取其它数值时,虽然其偏振态分布与“柠檬”结构相似,但是其光场中并没有圆偏振点,可将其称为“准柠檬”结构。
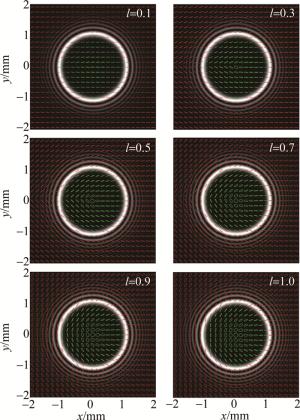
图 1 左旋圆偏振分量U1中不同拓扑荷(l≤1.0)时初始平面光场的偏振态分布
Figure 1. Polarization states of light fields in the initial plane for different values of topological charge (l≤1.0) in left-handed circularly polarized component U1
与之类似,将U1设置为右旋圆偏振、U2为左旋圆偏振时,初始平面光场的偏振态分布如图 2所示。此时初始平面的偏振态从接近于线偏振逐渐变化到“星”结构;当l取其它数值时,其偏振态分布可称为“准星”结构。

图 2 右旋圆偏振分量U1中不同拓扑荷(l≤1.0)时初始平面光场的偏振态分布
Figure 2. Polarization states of light fields in the initial plane for different values of topological charge (l≤1.0) in right-handed circularly polarized component U1
l>1.0时的情形同样值得关注,以U1为左旋圆偏振为例,当拓扑荷l取值为1.1、1.3、1.5、1.7、1.9和2.0时,初始平面的偏振态分布如图 3所示。结合图 1中l=1.0的情形,图 3展示了光场从“柠檬”到高阶偏振奇异光场的演化过程。
-
对于圆艾里光束,无论是否携带涡旋相位,其在自由空间传输时的光场都无法用解析式U(r, φ, z)来表示,因此只能用数值模拟的方式来展现其在某特定传输距离z时的光场分布。在此采用角谱的方法来进行计算,即在初始平面通过快速傅里叶变换将其变换到频域,通过乘以传递函数,得到传输距离z处的频谱,再经过快速傅里叶逆变换,得到其在z处空域的光场分布[29]。对于传输距离z,分别选取为100 mm,400 mm,464 mm和500 mm,可以数值模拟U1和U2在各传输距离的光强分布。其中对于U1,分别选取l=0.5和l=1.5为例,如图 4所示。可以看到,无论是否携带涡旋相位,也无论拓扑荷l的数值,随着传播距离z的不断变大,U1和U2主光环的尺寸在不断减小,这印证了圆艾里光束的自聚焦特性。在传输距离z=464 mm时,光场尺寸达到最小值,而后又随着传输距离不断变大,即二者的焦距均为464 mm。

图 4 不同传输距离z时U1和U2的光场强度分布
Figure 4. Intensity distribution of light fields U1 and U2 at different propagation distances z
根据图 4中两个正交圆偏振分量的光场分布,可以计算得出在传输距离z处叠加光场的偏振态分布,如图 5所示。需注意的是, 图 5中第1列光场尺寸是3 mm×3 mm,而后3列的光场尺寸为1 mm×1 mm。从图示来看,光场中偏振椭圆的分布规律并不明显,将在下一节中讨论这一问题。
-
为研究光场的拓扑结构,斯托克斯相位是一个非常重要的参量[30]。斯托克斯相位场中的相位奇异点对应矢量光场中的偏振奇异点,其表达式为[30]:
$ S_{12}=S_1+\mathrm{i} S_2 $
(3) 式中: S1、S2分别为斯托克斯参量; i为虚数单位。斯托克斯相位ϕ=arctan(S2/S1),对于U1, l=0.5+U2, l=0, 在不同传输距离z处的斯托克斯相位场计算如图 6所示。在初始平面,斯托克斯相位从-π/2变化到π/2;而在其传输过程中,其相位的变化均为从-π到π。在传输过程的初段,可以看到其中心涡旋结构遭到破坏,经过一段距离之后,如z为464 mm和500 mm处,发现相位场中又至少出现了一个相位奇异点,如图中红色圆圈所示。

图 6 叠加光场U1, l=0.5+U2, l=0在不同传输距离z处的斯托克斯相位场
Figure 6. Stokes phase fields of superposed light fields U1, l=0.5+U2, l=0 at different propagation distances z
如果将传输距离z=464 mm和z=500 mm两处的光场尺寸缩放到0.2 mm×0.2 mm,这个局部区域的光场偏振态分布如图 7所示。图中黄线表示S1=0,蓝线表示S2=0,两者交点,即图中实心红圆即为偏振奇异点。也就是说在初始平面不存在偏振奇异点的情况下,经过一定距离的传输,光场中出现了偏振奇异点。

图 7 U1, l=0.5+U2, l=0中心为0.2 mm×0.2 mm的区域在不同传输距离z的偏振态分布
Figure 7. Polarization states of the center section 0.2 mm×0.2 mm of U1, l=0.5+ U2, l=0 at different propagation distances z
对于U1, l=1.5+U2, l=0的情形,不同传输距离的斯托克斯相位场如图 8所示。由图可以看出,在初始平面,斯托克斯相位场仅包含一个相位奇异点,而在传输距离z=464 mm和z=500 mm处,至少都包含两个相位奇异点。
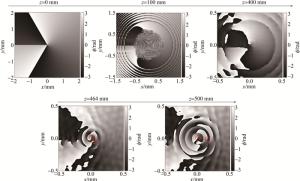
图 8 叠加光场U1, l=1.5+U2, l=0在不同传输距离z处的斯托克斯相位场
Figure 8. Stokes phase fields of superposed light fields U1, l=1.5+U2, l=0 at different propagation distances z
同样地,可以得出在z=464 mm和z=500 mm处中心0.2 mm×0.2 mm区域的偏振态分布,如图 9所示。结合图 8可以看出,在传输初期拓扑结构遭到破坏的情况下,经过一定的传输距离之后依旧可以重建,并且出现了更多的偏振奇异点。结合图 7可以看出,基于圆艾里光束的分数偏振奇点在空间中传播时拓扑结构的可恢复性,利用这一特性可将该偏振奇点用于自由空间光通信中。
-
由于圆艾里光束的自聚焦特性,叠加光场在传播过程之初,主瓣半径不断减小直至其焦点;由于分数涡旋光束的传输特性,叠加光场在传输之初存在缺口,然后得以闭合。无论其在初始平面有无C点,当叠加光场传输到焦点时,光场中出现了C点,并在焦点之后的传输过程中将出现更多的C点。与基于整数圆艾里涡旋光束的偏振奇异光场相比[13],两者均具有奇异拓扑结构的自恢复特性,然而基于分数的涡旋光束会给恢复后的光场中带来更多的C点。该工作从理论和数值模拟研究了对基于分数涡旋光束的偏振奇异光场在自由空间传输时拓扑结构的演变规律,为其应用提供理论基础。
基于分数涡旋光束的偏振奇点传输特性研究
Study of propagation characteristics of polarization singularities based on fractional vortex beams
-
摘要: 为了研究基于分数涡旋光束的偏振奇点在自由空间的动态传输特性, 采用数值模拟的方法, 进行了理论分析和数据仿真, 得到基于分数圆艾里涡旋光束的偏振奇点在自由空间传输时拓扑结构的演变。结果表明, 无论在初始平面内是否含有圆偏振奇点, 基于分数圆艾里涡旋光束的偏振奇点的自聚焦特性都会在传播过程中影响光场的拓扑结构, 使得光场在传输之初并不包含圆偏振奇异点, 但是在经过其自聚焦距离传输之后, 光场中将会出现若干个圆偏振奇点; 与基于整数圆艾里涡旋光束的偏振奇点相比, 两者均具有奇异拓扑结构的自恢复特性, 而基于分数的涡旋光束会给恢复后的光场中带来更多的圆偏振奇点。该工作将加深对偏振奇点传输特性的理解, 为其应用提供理论基础, 并拓宽圆艾里光束的应用范围。Abstract: In order to study the propagation characteristics of the polarization singularity based on the fractional vortex beam in free space, the method of numerical simulation was adopted, the theoretical analysis and data simulation were carried out, and the evolution of topology of polarization singularity based on the fractional circular Airy vortex beam was obtained during propagation in free space. The results show that regardless of whether there is a circular polarization singularity in the initial plane, the self-focusing properties of the polarization singularity based on the fractional circular Airy vortex beam will affect the topology of the light field during the propagation process, making the light field doesn't contain circular polarization singularities at the beginning of transmission, but after traveling through its self-focusing distance, several circular polarization singularities will appear in the light field. Compared with polarization singularities based on integer circular Airy vortex beams, both have singular topology self-recovery properties, while fractional-based vortex beams will bring more circular polarization singularities into the recovered light field point. This work will deepen the understanding of the propagation characteristics of polarization singularities, provide a theoretical basis for its application, and broaden the application range of circular Airy beams.
-
-
[1] DENNIS M R, O'HOLLERAN K, PADGETT M J. Singular optics: Optical vortices and polarization singularities[J]. Progress in Optics, 2009, 53: 293-363. [2] RUCHI SENTHILKUMARAN P, PAL S K. Phase singularities to polarization singularities[J]. International Journal of Optics, 2020, 2020: 2812803. [3] NYE J F, BERRY M V. Dislocations in wave trains[J]. Proceedings of the Royal Society of London A, 1974, 336(1605): 165-190. [4] ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbi-tal angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185 [5] BERRY M V. Optical vortices evolving from helicoidal integer and fractional phase steps[J]. Journal of Optics, 2004, A6(2): 259-268. [6] LEACH J, YAO E, PADGETT M J. Observation of the vortex structure of a non-integer vortex beam[J]. New Journal of Physics, 2004, 6(1): 71. [7] GBUR G. Fractional vortex Hilbert's hotel[J]. Optica, 2016, 3(3): 222-225. doi: 10.1364/OPTICA.3.000222 [8] 熊光昀, 唐奥, 兰斌, 等. 基于连续镜面变形镜本征模方法的复杂涡旋光场调控[J]. 光电工程, 2022, 49(11): 220066. XIONG G Y, TANG A, LAN B, et al. Vortex field manipulation based on deformation mirror with continuous surface[J]. Opto-Electron Engineering, 2022, 49(11): 220066. [9] WANG Q, TU Ch H, LI Y N, et al. Polarization singularities: Progress, fundamental physics, and prospects[J]. APL Photonics, 2021, 6(4): 040901. doi: 10.1063/5.0045261 [10] BECKLEY A M, BROWN T G, ALONSO M A. Full poincaré beams[J]. Optics Express, 2010, 18(10): 10777-10785. doi: 10.1364/OE.18.010777 [11] SHVEDOV V, KARPINSKI P, SHENG Y, et al. Visualizing pola-rization singularities in Bessel-Poincaré beams[J]. Optics Express, 2015, 23(9): 12444-12453. doi: 10.1364/OE.23.012444 [12] GARCIA-GRACIA H, GUTIÉRREZ-VEGA J C. Polarization singularities in nondiffracting Mathieu-Poincaré beams[J]. Journal of Optics, 2016, 18(1): 014006. doi: 10.1088/2040-8978/18/1/014006 [13] YE D, PENG X Y, ZHOU M Ch, et al. Simulation of generation and dynamics of polarization singularities with circular Airy beams[J]. Journal of the Optical Society of America, 2017, A34(11): 1957-1960. [14] SUN W Y, YE D. Simulated generation of fractional polarization singularities based on fractional vortex beam[J]. Optik, 2021, 242: 167201. doi: 10.1016/j.ijleo.2021.167201 [15] ZHAN Q W. Trapping metallic Rayleigh particles with radial polarization[J]. Optics Express, 2004, 12(15): 3377-3382. doi: 10.1364/OPEX.12.003377 [16] HNATOVSKY C, SHVEDOV V, KROLIKOWSKI W, et al. Revealing local field structure of focused ultrashort pulses[J]. Physical Review Letters, 2011, 106(12): 123901. doi: 10.1103/PhysRevLett.106.123901 [17] 谢有朋, 张珊, 雷霆, 等. 奇点光束复用光通信[J]. 光通信研究, 2018, 210(6): 11-20. XIE Y P, ZHANG Sh, LEI T, et al. Singular optical beams multiplexing optical communication[J]. Study on Optical Communications, 2018(6): 11-20(in Chinese). [18] ZHANG G L, CAI M Q, HE X L, et al. Pseudo-topological property of Julia fractal vector optical fields[J]. Optics Express, 2019, 27(9): 13263-13279. doi: 10.1364/OE.27.013263 [19] LAROCQUE H, SUGIC D, MORTIMER D, et al. Reconstructing the topology of optical polarization knots[J]. Nature Physics, 2018, 14(11): 1079-1082. doi: 10.1038/s41567-018-0229-2 [20] OTTE E, ALPMANN C, DENZ C. Polarization singularity explosions in tailored light fields[J]. Laser & Photonics Reviews, 2018, 12(6): 1700200. [21] 陈海涛, 李婷, 高曾辉. 非相干叠加光束携带C点偶极子的演化特性[J]. 激光技术, 2022, 46(5): 691-696. CHEN H T, LI T, GAO Z H. The evolution of C-dipole by incohe-rent superposition beams[J]. Laser Technology, 2022, 46(5): 691-696(in Chinese). [22] ZHANG G L, TU Ch H, LI Y N, et al. Observation of polarization topological singular lines[J]. Photonics Research, 2019, 7(6): 705-710. doi: 10.1364/PRJ.7.000705 [23] GU B, HU Y Q, ZHANG X H, et al. Angular momentum separation in focused fractional vector beams for optical manipulation[J]. Optics Express, 2021, 29(10): 14705-14719. doi: 10.1364/OE.423357 [24] EFREMIDIS N K, CHEN Zh G, SEGEV M, et al. Airy beams and accelerating waves: An overview of recent advances[J]. Optica, 2019, 6(5): 686-701. doi: 10.1364/OPTICA.6.000686 [25] EFREMIDIS N K, CHRISTODOULIDES D N. Abruptly autofocusing waves[J]. Optics Letters, 2010, 35(23): 4045-4047. doi: 10.1364/OL.35.004045 [26] CHEN B, CHEN Ch D, PENG X, et al. Propagation of sharply autofocused ring Airy Gaussian vortex beams[J]. Optics Express, 2015, 23(15): 19288-19298. doi: 10.1364/OE.23.019288 [27] 高金金, 周正兰, 徐华锋, 等. 部分相干Airy涡旋光束在非Kolmogorov谱中的模态强度[J]. 激光技术, 2021, 45(4): 522-529. GAO J J, ZHOU Zh L, XU H F, et al. Modal intensity of partially coherent Airy vortex beams in non-Kolmogorov turbulence[J]. Laser Technology, 2021, 45(4): 522-529(in Chinese). [28] 许森东. 艾里涡旋光束通过负折射率介质的传输特性[J]. 激光技术, 2022, 46(6): 850-854. XU S D. Study on propagation properties of vortex Airy beams through negative index medium[J]. Laser Technology, 2022, 46(6): 850-854(in Chinese). [29] GOODMAN J W. Introduction to Fourier optics[M]. 4th ed. New York, USA: Robort & Company Publisher, 2017: 61-67. [30] FREUND I, MOKHUN A I, SOSKIN M S, et al. Stokes singularity relations[J]. Optics Letters, 2002, 27(7): 545-547. doi: 10.1364/OL.27.000545 -


 网站地图
网站地图

 下载:
下载:





