-
随着科技的飞速发展,某些领域对关键零部件的加工要求越来越高,传统的激光加工已经逐渐不能满足加工工艺要求,水导激光加工技术应运而生[1-3]。水导激光加工技术是指将激光束射入一个加压水腔,在喷嘴口处聚焦,从而在出射水束中完成全反射,利用耦合后形成的“水束光纤”进行加工的技术[4-6]。激光束在水束中实现全反射,水束相当于固体光纤实现激光的导引。因此,只有光滑准直稳定的水束才能实现水和激光高效耦合,稳定水束的生成与控制是关键。
为了探究高质量稳定水束的生成规律,国内外大量学者对喷嘴结构及其内部的液流现象展开了研究。1975年,STERLING等人发现在不同喷嘴直径和流速情况下,水射流的稳定长度不同,且受到射流器件结构的影响[7]。1982年,REITZ发现空化现象取决于喷嘴的几何形状,并推测其可能是水射流破裂的原因之一[8]。2003年,WAGNER等人研究了喷嘴直径和水流速度对水射流稳定长度的影响,并将三者的关系绘成了直观的曲线图[9]。2004年,BEGENIR等人通过实验观察的方法研究了喷嘴几何形状对高雷诺数水射流的影响[10]。同年,TAFRESHI和POURDEYHIMI模拟了微喷嘴内部的空化和液力翻转[11]。2006年,CHEN等人对高压水射流进行了可视化的模拟仿真,发现淹没射流的能量耗散要远大于非淹没射流,并比较了射流在3种喷嘴结构下的表现[12]。2007年,SOU等人研究了空化数和雷诺数对2维喷嘴内空化和射流的影响[13]。2012年,SUN研究了喷嘴直径和入口压力对水射流稳定长度的影响[14]。次年,FU等人采用数值模拟的方法对水射流进行了分析,探究了水射流最大稳定长度与入口速度的关系[15]。2014年,LIN对圆形喷嘴内部的流型进行了分析,并讨论了不同压力的情况下,喷嘴内部流型及临界空穴数的变化[16]。2020年,YANG等人对平面缩流喷嘴内流场进行了仿真研究,探究了喷嘴几何参量以及系统雷诺数对缩流型水束形成的影响[17]。空化现象是水束稳定影响的1个主要因素,而空化现象直接对水束稳定的研究还未见报道。
高压水射流因为其机理复杂,且难以观察,目前很难用纯解析法和实验法研究。借助计算流体动力学,可以对喷嘴内部的流场进行简化和分析,并将流场分析结果进行可视化呈现。本文作者以水导激光应用中的典型喷嘴结构下出射到空气的水射流束为研究对象,进行贴合实际的建模,在不同入口压力下进行数值模拟,分析空化现象对水射流出射情况的影响规律,为水导激光中喷嘴结构和参数选择提供参考。
-
本研究中采用流体体积法(volume of fluid, VOF)模拟多相流[18]。在形成射流水束的过程中,喷嘴入口处压力可能低于饱和蒸汽压力使水中气核溢出,形成空化现象[19]。因此,设定VOF模型的三相为空气、水和蒸汽,在整个域中求解单个动量方程,得到所有相共用的速度场。射流过程中水与环境的热交换可以忽略,因此无需求解能量方程。
连续性方程:
$ \frac{\partial}{\partial t}\left(\rho_{\mathrm{m}}\right)+\nabla \cdot\left(\rho_{\mathrm{m}} \boldsymbol{v}_{\mathrm{m}}\right)=0 $
(1) 式中: t表示时间; ∇为散度算符; vm是所有相共用速度; ρm是混合密度。ρm由下式计算:
$ \rho_{\mathrm{m}}=\sum\limits_{k=1}^3 \varphi_k \rho_k $
(2) 式中: φ表示体积分数; k=1,2,3分别表示空气、水、蒸汽。动量方程为:
$ \begin{gathered} \frac{\partial}{\partial t}\left(\rho_{\mathrm{m}} \boldsymbol{v}_{\mathrm{m}}\right)+\nabla \cdot\left(\rho_{\mathrm{m}} \boldsymbol{v}_{\mathrm{m}} \boldsymbol{v}_{\mathrm{m}}\right)= \\ \nabla p+\nabla \cdot\left[\mu_{\mathrm{m}}\left(\nabla \boldsymbol{v}_{\mathrm{m}}+\nabla \boldsymbol{v}_{\mathrm{m}}{ }^{\mathrm{T}}\right)\right] \end{gathered} $
(3) 式中:p是压力; μm是混合相的动力粘度,$ \mu_{\mathrm{m}}=\sum\limits_{k=1}^3 \varphi_k \mu_k$。动量方程通过材料的ρm和μm受所有相体积分数的影响。
空化过程中的气泡动力学方程可以由Rayleigh-Plesset方程推导得出:
$ R \frac{\mathrm{d}^2 R}{\mathrm{~d} t^2}+\frac{3}{2}\left(\frac{\mathrm{d} R}{\mathrm{~d} t}\right)^2=\frac{p_{\mathrm{b}}-p}{\rho_1}-\frac{2 \sigma}{\rho_1 R}-4 \frac{\gamma_1}{R} \frac{\mathrm{d} R}{\mathrm{~d} t} $
(4) 式中: R是气泡半径; σ是表面张力系数; γl是液相的运动粘性系数; pb是气泡表面压力; p是局部远场压力,通常认为气泡表面压力pb等于饱和蒸气压,局部远场压力p取计算单元中心压力。忽略2阶相和表面张力相,气泡动力学方程变为:
$ \frac{\mathrm{d} R}{\mathrm{~d} t}=\sqrt{\frac{2}{3} \frac{p_{\mathrm{b}}-p}{\rho_{\mathrm{l}}}} $
(5) 空化模型采用Schnerr和Sauer模型,蒸汽体积分数方程为:
$ \frac{\partial}{\partial t}\left(\varphi_{\mathrm{v}} \rho_{\mathrm{v}}\right)+\nabla \cdot\left(\varphi_{\mathrm{v}} \rho_{\mathrm{v}} \boldsymbol{v}_{\mathrm{m}}\right)=\frac{\rho_{\mathrm{v}} \rho_{\mathrm{l}}}{\rho_{\mathrm{m}}} \frac{\mathrm{d} \varphi_{\mathrm{v}}}{\mathrm{d} t} $
(6) 式中:等号右边表示净质量源项RMT; φv是蒸汽相的体积分数,它与气泡数量密度nb之间的关系为:
$ \varphi_{\mathrm{v}}=\frac{n_{\mathrm{b}} \frac{4}{3} {\rm{ \mathsf{ π} }} R^3}{1+n_{\mathrm{b}} \frac{4}{3} {\rm{ \mathsf{ π} }} R^3} $
(7) 根据式(5)和式(8),经过推导,蒸汽的净质量源项变为:
$ R_{\mathrm{MT}}=\frac{\rho_{\mathrm{v}} \rho_{\mathrm{l}}}{\rho_{\mathrm{m}}} \varphi_{\mathrm{v}}\left(1-\varphi_{\mathrm{v}}\right) \frac{3}{R} \sqrt{\frac{2}{3} \frac{\left(p_{\mathrm{b}}-p\right)}{\rho_{\mathrm{l}}}} $
(8) 气泡半径R的表达式可由式(8)变形而来:
$ R=\left(\frac{\varphi_{\mathrm{v}}}{1-\varphi_{\mathrm{v}}} \frac{3}{4 {\rm{ \mathsf{ π} }}} \frac{1}{n_{\mathrm{b}}}\right)^{\frac{1}{3}} $
(9) 因此,只需要指定气泡数量密度nb,即可确定蒸汽相的体积分数变化,进而求解动量方程。Schnerr和Sauer模型设定气泡密度为1013/m3,饱和蒸汽压取默认的环境温度下水的汽化压力3540 Pa,采用算子分裂隐式压力的方式耦合压力场和速度场。压力方程和其它连续方程分别采用PRESTO! 法和Second Order Upwind法进行离散化处理,界面采用几何重构法计算体积分数。
-
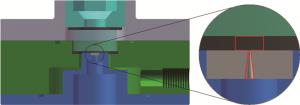
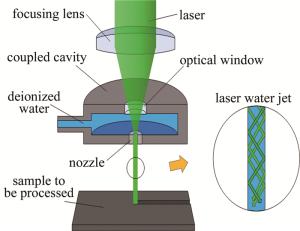
水导激光加工原理如图 1所示。经过聚焦透镜的激光束通过光学窗口进入耦合水腔,聚焦到水腔出口喷嘴处,与水束进行耦合。激光束在微细水柱的水-空气界面进行全反射,形成水束光纤,实现激光束的导引,对工件进行加工。
如何生成稳定的微水束,是实现激光束在水柱中全反射、形成水束光纤的关键。流体经过薄壁孔口出流时,由于流线不能突然转折,故而会形成一个流束直径最小的收缩断面,发生缩流现象,此时流束的直径约为喷嘴直径的80%[10, 20-21]。为了确保发生对生成稳定微水束有正向作用的缩流现象,研究中多采用入口处为锐边的喷嘴。但锐边喷嘴在带来缩流现象的同时,也带来了空化现象。空化现象是指在液体内部由于局部压力低于饱和蒸气压力值而导致的气核生长和溃灭的现象。空化会改变射流的密度和粘度,进而影响射流的速度和稳定性。
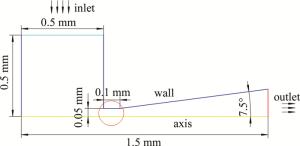
图 2是耦合腔结构,流体区域根据实际情况建模。水流从侧面进入腔室,因此设定压力入口在侧面,入口压力的取值范围为0.2 MPa~16 MPa,并在上下壁面附近添加边界层,出口为压力出口,设定出口压力为101325 Pa,即标准大气压的值,如图 3所示。其中喷嘴部分长度为1 mm,入口直径为0.1 mm,圆柱形流道部分长度为0.1 mm,锥形流道的角度为15°。为保证仿真结果的准确性,在喷嘴口附近对网格进行加密,如图 4所示。
-
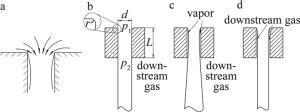
微水束外表面光滑平直是激光束能在水束和空气界面发生全反射的必要条件[4]。为了保证生成光滑平直的水束,最好的办法是使水束不与喷嘴流道内壁面接触,以免喷嘴内壁的加工质量影响生成水束的质量。腔体中的液体在进入喷嘴时,具有一定的动量,如果喷嘴上边缘锐利,那么液流就不会贴合喷嘴形状流动,而是会在喷嘴入口处收缩,与喷嘴分离,发生缩流现象,如图 5a所示。从喷嘴出射的水流大致可以分为3种流型,分别是单相流、空穴流和翻转流[4]。如果喷嘴入口上边缘是圆角或者水压不高时,就会形成如图 5b所示的单相流,它的特点是水束贴着喷嘴内壁流下,水束质量受喷嘴内壁加工质量影响。如果喷嘴入口上边缘锐利并且水压足够,就会发生缩流现象,之后依据喷嘴直径、流道长度、入口压力等参数的不同,可能形成图 5c所示的空穴流或者图 5d所示的翻转流。空穴流不稳定,水束呈发散状,不符合水导激光技术的要求;翻转流状态稳定,水束被下游空气包裹,不与喷嘴内壁接触,最适合用于生成水束光纤。
不同雷诺数的射流在出射时的表现有所不同。当雷诺数较大时,缩流后的水束可以在通过喷嘴流道之前不与喷嘴内壁面发生接触,形成图 5d所示的翻转流;而雷诺数较小的射流会在到达锥形流道之前与圆柱段流道发生接触,形成图 5c所示的空穴流,并会在稳定后发展成图 5b所示的单相流。这种水流与喷嘴脱离后又重新与流道接触的现象被称为再附着现象。
-
雷诺数的计算公式为:
$ R e=\frac{d \rho v}{\mu} $
(10) 式中: μ是水的动力粘度; d是特征长度,在这里取值为喷嘴圆柱段的直径; ρ是水的密度; v为喷嘴入口处水流速度值,由以下式计算得到:
$ v=K \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}} $
(11) 式中: K是流量系数; p1、p2分别代表入口压力和出口压力。
经过整理后雷诺数计算公式变为:
$ R e=\frac{K d \rho}{\mu} \sqrt{\frac{2\left(p_1-p_2\right)}{\rho}} $
(12) 经过多次仿真计算,将设定的入口压力p1、出口压力p2以及仿真得到的喷嘴入口处速度值代入式(12),确定式中流量系数K=0.6,这一数值与文献中的实验数据有较好的一致性[10, 20-22]。
-
首先探究在不考虑空化的前提下雷诺数对再附着长度的影响,仿真结果如图 6所示。实验室实际供液设备最多能产生16 MPa的压力,因此本次仿真的雷诺数范围从1195~10691变化,对应的入口压力范围为0.2 MPa~16 MPa。从图 6中可以发现,当雷诺数比较小时,水射流与壁面没有发生分离,也没有再附着现象产生。随着雷诺数的增大,水流在进入喷嘴时的动量使得射流脱离壁面,但是短暂地脱离后水流再次附着到壁面,发生再附着现象。

图 6 无空化作用、不同雷诺数时水射流再附着情况
Figure 6. Reattachment of water jets at different Reynolds numbers without cavitation
为方便与下文中添加空化模型的情况对比,提取雷诺数为1690时水射流随时间的变化情况,如图 7所示。可以看到,当发生再附着现象之后,水射流和喷嘴壁面之间形成了一个封闭的空气循环区,随后其中的空气破裂,对射流产生扰动,使得水流充满整个区域。当水射流趋于稳定时,完全贴附于喷嘴的圆柱段流道内壁流出,并与部分锥形流道粘连。在这种情况下形成的水射流不再具备光滑和平直特性。
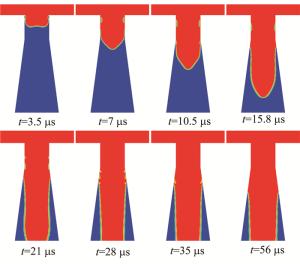
图 7 无空化作用、雷诺数为1690时不同时刻射流相图
Figure 7. Jet phase diagram at different times at Reynolds number 1690 without cavitation
将不同雷诺数对应的再附着长度进行归一化处理,结果如图 8所示。可以看出,在低雷诺数时水流的水平动量不足以使射流和喷嘴壁面分离,随着雷诺数的上升,逐渐产生再附着现象,并且雷诺数越大,再附着长度也越大。
-
通过对空化现象的了解,已知当水射流中的压力低于饱和蒸汽压力为3540 Pa时,水中的气核会溢出,出现空化现象。在上述雷诺数为1690的仿真中,实际压力情况已经满足空化现象出现的条件,但水流最终充满喷嘴内部,在低压区并未产生气泡,形成空化现象,这与现实不符。计算此时的空穴数和临界空穴数,代入喷嘴内部流型决策树[4, 16],结果同样显示为翻转流流型。整理无空化模型的仿真数据发现,在入口压力小于6 MPa,即雷诺数小于6547时,水束达到稳定状态均不能形成翻转流,这也与实际情况及参考文献有出入。因此在探究雷诺数对再附着长度的影响时,应该考虑空化现象的影响,添加空化模型,引入蒸汽气泡的生长过程,以使仿真结果更符合实际。
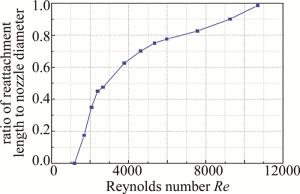
在添加空化模型的情况下,不同雷诺数时的水射流再附着情况如图 9所示。整理雷诺数与再附着长度的关系绘成折线图, 如图 10所示。从图中可以看出,随着雷诺数的增大,再附着长度也随之增大。
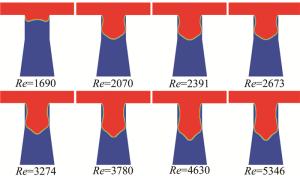
图 9 考虑空化作用、不同雷诺数时水射流再附着情况
Figure 9. Reattachment of water jets at different Reynolds numbers cavitation
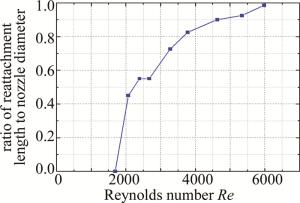
图 10 考虑空化作用、不同雷诺数时再附着长度与喷嘴直径之比
Figure 10. Ratio of reattachment length to nozzle diameter at different Reynolds numbers with cavitation
在考虑空化的情况下,雷诺数为1690时的水射流随时间的仿真结果如图 11所示。从图中可以看到,由于水平动量较小,水流几乎贴着喷嘴内壁流下,当射流充满喷嘴内部的时候,空化现象开始出现。t=7 μs时,由于负压的作用,水中的气核溢出,空泡开始产生,随后空泡不断生长,直到与空气接触。空泡与空气接触时发生破裂,水流又重新充满局部区域,这个过程会对射流造成扰动,使其变成不稳定的湍流状态。伴随着时间的流逝,上述过程不断重复,直到出射的水流不再与喷嘴壁面存在接触,水射流达到稳定状态。在考虑空化的情况下,由于空化现象而产生的空泡不断生长,使得射流最终脱离喷嘴壁面,其质量不再受喷嘴壁面加工质量的影响,可以满足水与激光耦合的要求。
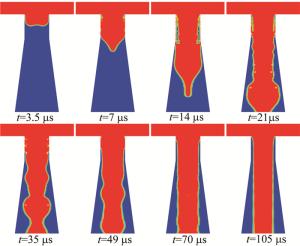
图 11 考虑空化作用、雷诺数为1690时不同时刻射流相图
Figure 11. Jet phase diagram at different times at Reynolds number 1690 with cavitation
从上述的例子可以看出,考虑空化的情况下,只要能够满足空化产生的条件,那么即使喷嘴内部充满了水最终也可以在空化的作用下形成翻转流,生成满足应用要求的水束。为了验证这一点,图 12模拟了入口压力为5 MPa、雷诺数为5977时水射流随时间的变化,初始喷嘴内部充满液体。从图中可以看到,在5977雷诺数的情况下,3.5 μs时空化现象开始产生,空泡开始生长。随着空泡的生长,逐渐在喷嘴的入口附近形成一个空气循环区,水射流不再贴附壁面流动。空气循环区慢慢扩大,数量极多的空泡产生又溃灭使得水射流始终处于不稳定的湍流状态,直到空气循环区生长到与外界大气连通,发生液力翻转。液力翻转现象发生后,压力恢复正常,空气将水射流和壁面分隔,空化现象停止,经过一段时间的整理后,不再受壁面摩擦和空化扰动影响的稳定水射流产生。
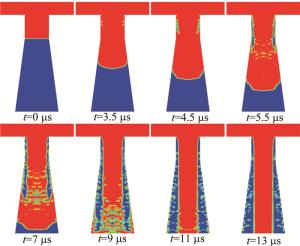
图 12 考虑空化作用、雷诺数为5977时不同时刻射流相图
Figure 12. Jet phase diagram at different times at Reynolds number 5977 with cavitation
将不考虑空化和考虑空化的情况放在同一张图中进行比较,如图 13所示。从图中可以看出,无论是否考虑空化,雷诺数对再附着长度的影响规律大致相同,都是随着雷诺数的增大,再附着长度也不断增大,两种情形下的线型也相似。但是两种情形在细节上有所不同,例如雷诺数相同时,考虑空化情形下射流的再附着长度比不考虑空化情形的要大。这是由于空泡的产生使得发生再附着现象的时间点延后,同时也延长了再附着长度。这对于喷嘴结构的设计有一定的指导意义。
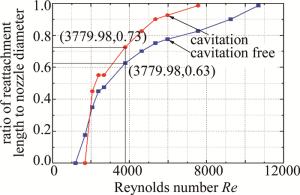
图 13 不同雷诺数、有无空化作用时再附着长度比较
Figure 13. Reattachment length at different Reynolds numbers without cavitation and with cavitation
尽管空化有助于形成翻转流,但是由于空化产生的气泡在破裂时造成的空蚀现象对喷嘴壁具有破坏性作用,因此要尽力避免在喷嘴内部充满液体时发生空化现象。如果采用无空化作用的数据,为了使射流在常用入口压力下形成翻转流,喷嘴圆柱段的长径比要小于0.6,如图 13所示。在这种情况下,雷诺数高于3780,即入口压力高于2 MPa的水射流都可以不与喷嘴壁面接触,顺利通过圆柱段,形成稳定水射流。而如果采用考虑空化作用的数据,喷嘴圆柱段的长径比只需要小于0.7,即可让入口压力高于2 MPa的水射流形成翻转流。喷嘴圆柱段的长径比与喷嘴的承压能力成正比,长径比越大,承压能力越强。因此,参考更符合实际的考虑空化作用的数据,可以在设计喷嘴结构时加大圆柱段的长径比,提高喷嘴的承压能力。
-
针对从典型锥形向上型喷嘴出射的水射流,分别在不考虑空化和考虑空化的条件下对其进行了喷嘴内部流场模拟,阐释了空化现象产生的原因及发展过程,并与不考虑空化作用的仿真结果进行了对比。
(a) 无论是否考虑空化作用,雷诺数的增长与水射流再附着长度的变化趋势一致。当雷诺数较小,水平动量不足以使水流与喷嘴壁面分离时,射流贴着壁面流下,不发生再附着现象;随着雷诺数增大,水流与壁面发生短暂分离后又重新贴附壁面,发生再附着现象,并且发生再附着的位置也逐步下移,直至接近圆柱段流道末端;当雷诺数足够大时,水流与壁面分离后顺利通过圆柱段流道,不发生再附着现象。
(b) 在入口压力小于6 MPa导致喷嘴内部充满水时,不考虑空化的情况下,水射流会完全贴附于喷嘴的圆柱段流道内壁流出,并与部分锥形流道粘连,无法形成翻转流流型,与实际情况和参考文献不符; 而考虑空化的情况时,只要低压区的压力小于饱和蒸气压,空化现象就会发生,空泡逐渐产生和生长直至接触空气, 此时,水射流不再贴附壁面流动,形成翻转流,稳定性得到提高。
(c) 空化现象会使得水射流的再附着长度提高。在雷诺数高于2070后,直到实验室设备所能达到的最大雷诺数10691,添加空化模型的射流再附着长度均高于不考虑空化的情况。真实地了解水射流的再附着长度有助于设计合理的喷嘴结构, 对于入口压力高于2 MPa的射流,只需保证喷嘴圆柱段长径比小于0.7,即可形成翻转流。合理的喷嘴结构可以减少喷嘴空蚀的可能性,提高其承压能力,对于延长喷嘴的使用寿命有重要意义。
空化现象对水导激光微水束稳定性的影响研究
Study on the influence of cavitation on the stability of water-guided laser micro-water beam
-
摘要: 为了探寻空化现象对水导激光微水束稳定性影响, 利用计算流体动力学的方法, 分别在不考虑空化和考虑空化的情况下, 对从典型喷嘴出射的水射流进行了数值模拟分析, 研究了空化现象的产生机理及对微水束稳定性的影响。结果表明, 在入口直径为0.1 mm、圆柱段长径比为1、上边缘锐利的喷嘴结构下, 随着入口压力从0.2 MPa增大到16 MPa, 水射流与喷嘴壁面分离后再次附着的长度逐渐增大, 并且空化会导致该长度延长; 在入口压力小于6 MPa的情况下, 不考虑空化的水射流在稳定后会贴着喷嘴壁面流下, 而添加空化模型使得水束形成翻转流。该研究对设计满足水导激光工艺的喷嘴结构有着重要的参考价值。Abstract: In order to explore the influence of cavitation on the stability of the micro-water beam of the water guide laser, the numerical simulation analysis of the water jet from a typical nozzle was carried out by using the computational fluid dynamics method without considering cavitation and considering cavitation respectively, and the generation mechanism of cavitation and its influence on the stability of the micro-water beam was studied. The calculation results show that under the nozzle structure with the inlet diameter of 0.1 mm, the length-diameter ratio of the cylinder section of 1, and the sharp upper edge, with the inlet pressure increasing from 0.2 MPa to 16 MPa, the re-attachment length of the water jet after separation from the nozzle wall gradually increases, and cavitation will lead to the extension of the length. When the inlet pressure is less than 6 MPa, the water jet, without considering cavitation, will flow down the nozzle wall after stabilization, and the addition of a cavitation model can make the water beam form a flipped flow. The simulation results have important reference values for the design of nozzle structures that meet the requirements of water-guide laser technology.
-
-
[1] 刘亚威. 激光微射流提供发动机零件加工新方案[J]. 航空动力, 2019(6): 44-47. LIU Y W. Laser microjet offers new solution for the machining of aero engine parts[J]. Aerospace Power, 2019(6): 44-47(in Chinese). [2] 顾新云, 申刚. 激光水切加工技术研究[J]. 中国高新科技, 2020(16): 128-129. GU X Y, SHEN G. Research on water jet assisted laser cutting technology[J]. ZHONG GUO GAO XIN KE JI, 2020(16): 128-129(in Chinese). [3] LIU Y, WEI M R, ZHANG T, et al. Overview on the development and critical issues of water jet guided laser machining technology[J]. Optics & Laser Technology, 2021, 137: 106820. [4] 李灵. 水导激光微细加工技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2008: 17-42. LI L. Study on water-jet guided laser micromachining technology[D]. Harbin: Harbin Institute of Technology, 2008: 17-42(in Ch-inese). [5] 李灵, 杨立军, 王扬, 等. 水导激光微细加工中激光与水束光纤耦合技术[J]. 光学精密工程, 2008, 16(9): 1614-1621. LI L, YANG L J, WANG Y, et al. Laser and water-jet fiber coupling technology for water-jet guided laser micromachining[J]. Optics and Precision Engineering, 2008, 16(9): 1614-1621(in Chinese). [6] RICHERZHAGEN B. Method and apparatus for machining material with a liquid- guided laser beam: US, 5902499 [P]. 1999-05-11. [7] STERLING A M, SLEICHER C A. The instability of capillary jets[J]. Journal of Fluid Mechanics, 1975, 68(3): 477-495. doi: 10.1017/S0022112075001772 [8] REITZ R D. Mechanism of atomization of a liquid jet[J]. Physics of Fluids, 1982, 25(10): 1730. doi: 10.1063/1.863650 [9] WAGNER F, SIBAILLY O, VÁGÓ N, et al. The laser microjet® technology-10 years of development[C]//ICALEO 2003. New York, USA: Laser Institute of America, 2003: 1-8. [10] BEGENIR A, TAFRESHI H V, POURDEYHIMI B. Effect of nozzle geometry on hydroentangling water jets: Experimental observations[J]. Textile Research Journal, 2004, 74: 178-184. doi: 10.1177/004051750407400215 [11] TAFRESHI H V, POURDEYHIMI B. Simulating cavitation and hydraulic flip inside hydroentangling nozzles[J]. Textile Research Journal, 2004, 74: 359-364. doi: 10.1177/004051750407400413 [12] 陈春, 聂松林, 吴正江, 等. 高压水射流的CFD仿真及分析[J]. 机床与液压, 2006(2): 103-106. CHEN Ch, NIE S L, WU Zh J, et al. A study of high pressure water jet characteristics by CFD simulation[J]. Machine Tool & Hydraulics, 2006(2): 103-106(in Chinese). [13] SOU A, HOSOKAWA S, TOMIYAMA A. Effects of cavitation in a nozzle on liquid jet atomization[J]. International Journal of Heat and Mass Transfer, 2007, 50(17/18): 3575-3582. [14] 孙胜廷. 水导引激光加工装置及加工特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 38-40. SUN Sh T. Research of water guided laser devices and its machining properties[D]. Harbin: Harbin Engineering University, 2012: 38-40(in Chinese). [15] 符永宏, 曹佳, 董非, 等. 微水导激光稳定水束光纤的CFD仿真研究[J]. 流体机械, 2013, 41(8): 21-25. FU Y H, CAO J, DONG F, et al. CFD simulation of the laser stable water beam in micro water-jet guided laser[J]. Fluid Machine-ry, 2013, 41(8): 21-25(in Chinese). [16] 林广森. 水导激光加工关键技术的研究[D]. 武汉: 华中科技大学, 2014: 8-16. LIN G S. Study on the key technology of water-jet guided laser machining[D]. Wuhan: Huazhong University of Science and Techno-logy, 2014: 8-16(in Chinese). [17] 杨林帆, 焦辉, 黄宇星, 等. 基于水导激光平面缩流喷嘴内流场仿真研究[J]. 激光技术, 2020, 44(6): 754-761. YANG L F, JIAO H, HUANG Y X, et al. Simulation study of the flow field in the plane convergent nozzle based on the water guide laser[J]. Laser Technology, 2020, 44(6): 754-761(in Chinese). [18] SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]//2001 International Conference on Multiphase Flow. New Orleans, USA: SCHNERR, 2016: 2-6. [19] TAFRESHI H V, POURDEYHIMI B. Cavitation and hydraulic flip[J]. Fluent News, 2004, 74(4): 38. [20] GHASSEMIEH E, VERSTEEG H K, ACAR M. Effect of nozzle geometry on the flow characteristics of hydroentangling jets[J]. Textile Research Journal, 2003, 74: 178-184. [21] NURICK W H. Orifice cavitation and its effects on spray mixing[J]. Journal of Fluids Engineering, 1976, 98(4): 681-687. doi: 10.1115/1.3448452 [22] 栾美玲, 郑家鑫, 孙相超, 等. 液体辅助激光加工硬脆材料及其应用[J]. 光电工程, 2023, 50(3): 220328. LUAN M L, ZHENG J X, SUN X Ch, et al. Liquid-assisted laser fabrication of hard materials and applications[J]. Opto-Electron Engineering, 2023, 50(3): 220328(in Chinese). -


 网站地图
网站地图

 下载:
下载: