-
全息显示技术能够把物体的波前完整地重建出来,提供真实的视觉感受,因而成为国内外真3维显示技术的研究热点[1-4]。计算全息是其中的一个重要部分,它是现代光学和计算机技术相结合的产物[5-6],它不需要搭建实际光路,通过计算机仿真计算就可以生成虚拟物体的全息图,具有很高的灵活性和重复性。目前生成计算全息图的方法主要分为两种: 一种是面元法[7-9],它的核心是将空间中的3维物体分割为许多不同形状的面元,把物光波视为这些面发出光波的叠加;另一种是点源法[10-13],它将空间中的3维物体采样离散为许多的点,物光波视为这些点发出光波的叠加。点源法具有原理简单、操作灵活的优势,而且通过点源法生成的计算全息图有着较好的重建质量,所以点源法有着巨大的潜力。但是,为了得到高质量的重建像,需要对3维物体采集大量的点数据,并进行大量运算,普通计算机很难达到生成计算全息图的实时计算的要求。
为了提高点源法的计算速度,LUCENT等人提出了查找表法(look-up table, LUT)[14]。LUT方法预先计算每个可能位置点源的干涉条纹图样并储存起来,实时计算时只需读取图样并进行叠加,极大地缩短了线上的运算时间,但是预先计算的数据表需要庞大的内存空间;基于点源模型计算全息图的另一种方法是波前记录平面法[12],其核心在于在物体附近定义一个平面,该平面与全息面平行且等大,计算每个点源在该平面上贡献的复振幅,而不需要计算在全息面的复振幅叠加。该算法通过降低计算机全息图(computer-generated hologram, CGH)的计算复杂度来大幅提高了计算速度,但是其缺点是不能记录大于全息图尺寸的物体。
随着计算机技术的快速发展,提高计算速度的方法不再局限于算法的改进,将高性能硬件与算法结合成为了广大学者更优的选择。日本学者使用可编程逻辑器件构建了专门用于全息计算的硬件系统[15],使全息图的计算速度有了巨大的提升,但是由于计算全息专用硬件系统的成本过高,所以没有被广泛地应用,相比之下,图像处理单元(graphic processing unit, GPU)低成本、高性能[16-20],因此成为了许多研究人员的首选。
AHRENBERG等人采用OpenGL对GPU编程,有效地提高了计算全息图的生成速度[21]。TAKADA等人使用多GPU系统计算生成全息图,使得计算速度得到极大的提升[22]。但是目前利用GPU生成计算全息图都是使中央处理器(central processing unit, CPU)和GPU以串行方式工作,CPU与GPU总是只会有一个在工作状态,另一个处于等待状态,硬件得不到充分利用,导致计算速度减慢。为了高效地利用CPU和GPU异构系统计算全息图的计算性能,本课题组先期已经做了初步的报道[23],但在这篇文献中只是简单地实现了CPU和GPU异构系统并行计算全息图,并未对该系统进行优化处理,存在着不足。本文中为了进一步优化CPU和GPU异构系统并行计算全息图的性能,提出了数据处理与任务调度重叠并行的计算方法, 然后基于CPU和GPU异构系统的重叠并行的计算方法,进行全息图计算公式简化、任务分配、共享内存优化等, 设计并实现了CPU-GPU异构系统用于快速生成计算全息图。
-
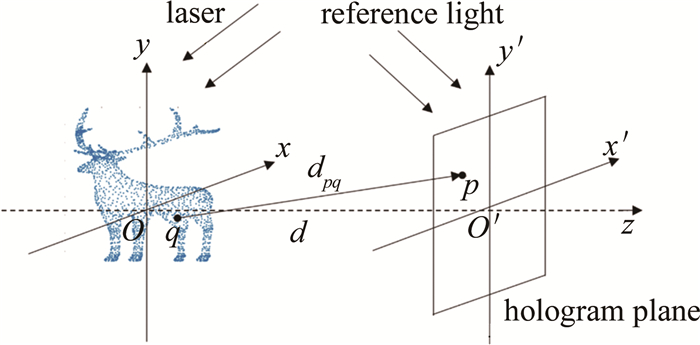
点源法将3维物体分解为离散的点云,所有点发出的球面波在全息面叠加从而得到3维物体在全息面的衍射场,该衍射场再与参考光波叠加得到3维物体的全息图,如图 1所示。
设3维物体的空间坐标系为Oxyz,全息图平面的空间坐标系为O′x′y′z′,两个坐标系的z轴在同一直线上,且两坐标系原点间的距离为d。若3维物体任意一点q的坐标为(xq, yq, zq),全息面上任意一点p的坐标为(xp′, yp′, zp′), 则点p与点q之间的距离dpq=$ \sqrt{\left(x_p{ }^{\prime}-x_q\right)^2+\left(y_p{ }^{\prime}-y_q\right)^2+\left(d-z_q\right)^2}$,p点接收到的光波复振幅可用下式表示:
$ U\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)=\frac{\left|U\left(x_q, y_q, z_q\right)\right|}{d_{p q}} \exp \left(\mathrm{j} k d_{p q}\right) $
(1) 式中: U(xq, yq, zq)为点q的光波复振幅; j是虚数单位; 波数k=2π/λ; λ是光波长。将全息面离散为像素点,就能通过式(1)计算出每个像素点上所有物点衍射到该点的光波场复振幅的叠加,得到3维物体的衍射场Ud(xp′, yp′, 0), 再将衍射场Ud(xp′, yp′, 0)与参考光R(xp′, yp′, 0)叠加得到全息图的复振幅分布Uh(xp′, yp′, 0):
$ \begin{aligned} & U_{\mathrm{h}}\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right): \\ & \quad U_{\mathrm{h}}\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)=U_{\mathrm{d}}\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)+R\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right) \end{aligned} $
(2) 式中: 参考光R(xp′, yp′, 0)为平面波。
$ R\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)=A \exp \left[\mathrm{j} k\left(x_p{ }^{\prime} \cos \alpha+y_p{ }^{\prime} \cos \beta\right)\right] $
(3) 式中: A为参考光振幅大小; cosα和cosβ为平面波传播的方向余弦; α和β分别表示平行光与x轴和y轴的夹角。最后,计算出Uh(xp′, yp′, 0),取其模长,并规约到[0,255]之间, 得到3维物体的振幅型计算全息图。
-
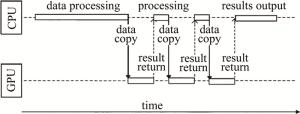
目前使用GPU加速点源法生成计算全息图通常是将总任务划分为一个个并行的小任务,并把这些可并行执行的任务放到GPU上,使用CPU喂给GPU数据,等GPU计算完后CPU再来接收数据,进行下一步处理与传输,这种工作方式在GPU与CPU间属于串行工作方式,其结构如图 2所示。当CPU计算数据时,GPU处于等待状态,而GPU做计算时,CPU处于空闲状态,这造成了CPU与GPU同时只会有一个是在工作状态,硬件得不到充分利用,导致计算速度缓慢。
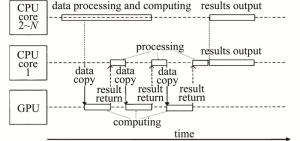
为了使CPU和GPU的性能得到充分的利用,本文作者将计算过程分成两部分:数据处理和任务调度。CPU不再仅承担任务调度的工作, 而是划分为两个部分:一部分仅包含一个CPU核心,用于承担任务的调度和数据的传输;另一部分由其余的核心构成,用来与GPU一同进行数据处理与计算。这样当某个GPU计算完一轮之后,单独的CPU核心会立即将数据接收,让GPU尽快进入下一轮的计算,以免数据堵塞拖慢速度。改进的CPU与GPU重叠并行的工作方式如图 3所示。图中,N表示CPU的总核心数,2~N表示第2个CPU核心到第N个CPU核心。通过计算策略的改进,很大程度上减少了GPU与CPU相互等待的时间,减少了计算耗时。
-
为提高算法在GPU部件上的运算计算,本文作者首先对衍射公式进行了简化。对式(1)进行泰勒展开并化简,可以得到:
$ \begin{aligned} & U\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)=\frac{\left|U\left(x_q, y_q, z_q\right)\right|}{\left|d-z_q\right|} \exp \left\{\mathrm{j} \frac{2 {\rm{ \mathsf{ π} }}}{\lambda} \times\right. \\ & \left.\left[\left(d-z_q\right)+\frac{\left(x_p{ }^{\prime}-x_q\right)^2+\left(y_p{ }^{\prime}-y_q\right)^2}{2\left(d-z_q\right)}\right]\right\} \end{aligned} $
(4) 再对式(4)进一步处理得:
$ \begin{gathered} U\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)= \\ \frac{A_q}{|\Delta z|} \exp \left[\mathrm{j}\left(\frac{2 {\rm{ \mathsf{ π} }} \Delta z}{\lambda}+\frac{{\rm{ \mathsf{ π} }}}{\lambda} \frac{\Delta x^2+\Delta y^2}{\Delta z}\right)\right] \end{gathered} $
(5) 式中: Aq=|U(xq, yq, zq)|; Δx=xp′-xq; Δy=yp′-yq; Δz=d-zq。由于GPU计算除法的性能极低,非常耗时,因此针对GPU的这一不足,对计算公式做出调整,将除法的计算次数尽量减少:
$ \begin{gathered} U\left(x_p{ }^{\prime}, y_p{ }^{\prime}, 0\right)= \\ \frac{A_q}{|\Delta z|} \exp \left[\mathrm{j} C\left(2 \Delta z+\frac{\Delta x^2+\Delta y^2}{\Delta z}\right)\right] \end{gathered} $
(6) 式中: C为常数,C=π/λ。在全息图的计算之前,可以预先计算常数C, 从而减少计算过程中执行不必要的操作,现在GPU中的除法运算就仅有两次。
同时,在GPU计算式(6)的过程中,最耗时的是欧拉公式展开后的三角函数的运算,尤其是在给正弦或余弦函数传入很大的参数值时,会极大地拖慢计算速度。为了提高计算速度,本文作者把传入三角函数的值对2π求余之后再传入三角函数。另外,虽然C语言中有现成的对浮点数求余的函数,但是它的内部实现做了过多的处理,仍不能使耗时减到最少,因此,使用下面的方法,来进行浮点数求余操作:
$ \theta^{\prime}=\theta-\operatorname{int}\left(\frac{\theta}{2 {\rm{ \mathsf{ π} }}}\right) \times 2 {\rm{ \mathsf{ π} }} $
(7) 式中: θ′是求余的结果; θ是求余之前的数; int(·)表示可以将小数点后的数舍弃。
-
CPU-GPU异构系统的任务调度是根据任务的不同属性和计算量,将其分配到合适的处理器中,实现任务的最优化分配。在CPU-GPU异构系统中,任务调度算法是至关重要的,只有找到最优的任务分配,CPU-GPU异构系统的计算性能才会达到最优。为了快速地寻找CPU-GPU异构系统的最优任务分配,采用了二分法搜索进行最优的任务分配。
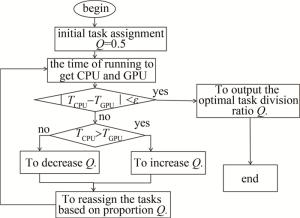
二分搜索算法进行任务优化如图 4所示。Q为任务划分比(Q=GPU任务量/CPU任务量),首先初始化任务划分,然后分别计算CPU和GPU执行的时间,当它们的时间差超过设定的阈值ε时,将比较CPU和GPU执行的时间TGPU和TCPU,若CPU花费时间更长,则减少CPU的任务量,增加GPU的任务量; 若GPU花费时间更长,则减少GPU的任务量,增加CPU的任务量,直到它们的时间差小于设定的阈值,此时认为CPU和GPU所分配到的任务量相同,硬件利用率达到最大。
因为不同的硬件环境CPU和GPU所分配到的最佳任务量是不同的,所以在每个新的硬件环境下都需要使用该方法提前计算出硬件环境下的最佳任务划分比,在使用CPU-GPU异构系统计算时,需要传入该比值,但是在同一硬件环境下任务划分比只需计算1次。
-
本文中分别在CPU-GPU异构系统和GPU系统中对多个3维模型进行了仿真实验,验证了CPU-GPU异构系统的高效性。在CPU-GPU异构系统中共使用16个CPU核心,核心的型号是11th Gen Intel(R) Core(TM)i7-11800H@ 2.3 GHz, 在CPU-GPU异构系统和GPU系统使用的GPU型号均为NVIDIA GetForce RTX 3060 Laptop GPU。仿真实验中全息图的分辨率为1024×1024,光波长为532 nm,衍射距离为1000 mm,实验得到的数据如表 1所示。从表中可以看出, CPU-GPU异构系统相比于GPU系统计算速度有4~4.75倍的提升。在物点数较少的时候,GPU系统计算耗时是CPU-GPU异构系统的4倍左右;在物点数较多的时候,GPU系统计算耗时是CPU-GPU异构系统的4.75倍左右。
表 1 CPU-GPU异构系统与GPU系统时间对比
Table 1. Time comparison between CPU-GPU heterogeneous system and GPU system
number of points 2354 4708 9416 11770 21174 42348 time spent by CPU-GPU system/ms 347 622 1138 1415 2521 4962 time spent by GPU system/ms 1417 2753 5366 6608 11840 23539 speedup ratio 4.08 4.43 4.72 4.67 4.70 4.74 number of points 101168 202336 404672 1018748 2037496 time spent by CPU-GPU system/ms 11763 23912 47558 120979 242568 time spent by GPU system/ms 56545 113783 227851 575493 1151167 speedup ratio 4.81 4.76 4.79 4.76 4.75 以点数量作为横坐标,花费时间作为纵坐标,分别做出两条曲线,如图 5所示。从图 5可以看出,两条曲线随着物点数增加,曲线距离变远,CPU-GPU异构系统相对于GPU系统的加速比逐渐提高。这是因为物点数很少的时候,GPU与CPU之间需要相互传输的数据量很少,可以在极短时间内完成; 而在物点数很多的时候,GPU与CPU之间就需要大量的传输数据,CPU-GPU异构系统可以在这种情况下一边传输数据一边做计算,相对GPU系统的加速比就更高。
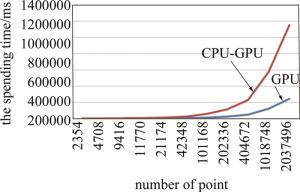
图 5 CPU-GPU异构系统与GPU系统时间对比曲线
Figure 5. Time comparison curve between CPU-GPU heterogeneous system and GPU system
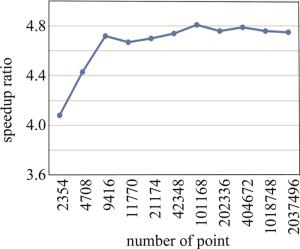
以物点数为横坐标,CPU-GPU异构系统相对与GPU系统的加速比为纵坐标作出一条曲线,如图 6所示。从图 6可以看出,在物点数量已经很多的时候,再继续增加物点数,CPU-GPU异构系统相对与GPU系统的加速比不再提高。其主要原因是:CPU-GPU异构系统在对大量点进行计算时,CPU和GPU同时工作,计算和数据传输同时进行,系统已经达到了满负载的工作状态,此时再增加物点数量, 系统的计算速度也已不再提高,因此,相对GPU系统的加速比也就不再变化。
-
为了验证CPU-GPU异构系统是有效可行的,使用的两个3维模型(如图 7所示)在该系统中生成全息图后,再在计算机中模拟光学再现实验。实验结果如图 8所示。
模拟实验的记录距离和重建距离均为2000 mm,全息面尺寸为10 mm×10 mm,采样数为1024×1024,光波长为0.000523 mm。从实验结果来看,利用CPU-GPU异构系统生成的计算全息图可以成功再现3维物体, 从而证明了该CPU-GPU异构系统是有效可行的。
-
在点源模型计算全息图的原理上,设计了基于多核CPU和GPU的异构并行系统,并对该系统使用了全息图计算公式简化、任务分配、共享内存等优化方法,提高了CPU-GPU异构系统的计算性能,实验验证了系统的可行性。在本文中的硬件条件下,实验结果表明, 计算全息图的加速比较GPU系统的加速比至少提高4倍左右,说明设计的系统能有效地解决点源模型计算全息图缓慢的问题。
在今后的实验中,本文作者准备采用更高性能的GPU和CPU,从而达到全息图的实时计算。但实际上,在GPU性能有大幅提升的情况下,CPU的性能也应同步提升,否则在GPU性能远远超过CPU性能时,使用异构系统反而会让运算速度较GPU系统的运算速度更慢。这是因为高性能的GPU能快速地将高并发的大量任务在短时间内完成,而数据的传输任务只能靠CPU串行执行,当CPU性能过差时,就会导致在传输数据上花费过多时间,并且能分配给CPU执行的任务量也较少。因此,提升CPU性能是很有必要的,它不仅能帮GPU承担更多的任务量,而且能及时将处理完成的数据传走,并喂进新的数据,让GPU处于满负荷的工作状态, 使该异构系统的计算速度得到很大的提升。
使用多核CPU-GPU异构系统快速生成计算全息图
Fast generation of CGH using multi-core CPU-GPU heterogeneous system
-
摘要: 为了充分利用计算机的计算性能提高基于点源模型的计算全息图(CGH)的生成速度, 设计了基于多核中央处理单元(CPU)和图形处理单元(GPU)的计算全息图快速生成系统, 并对该系统进行了优化。首先采用统一架构平台设计并实现了基于点源模型的计算全息图生成系统, 提出了计算的优化策略; 然后根据优化的计算公式来减少计算量; 最后对任务调试等进行优化, 构建CPU的并行计算系统, 其中一个核心负责启动函数和传输数据, 其余核心承担一部分计算任务, 进一步提高计算速度。结果表明, 设计的系统能让CPU和GPU的性能均得到充分利用, 在同等配置的计算硬件条件下, 生成计算全息图的加速比较GPU系统计算全息图的加速比提高了4~4.75倍, 可以有效提高计算全息图的生成速度。该研究对快速生成3维场景全息图是有帮助的。Abstract: In order to make full use of the computing performance of the computer to improve the speed of computer-generated hologram(CGH) based on the point source model, a fast CGH generation system based on a multi-core central processing unit (CPU) and graphics processing unit (GPU) was designed and optimized in this paper. First of all, the system used the unified architecture platform to design and implement a CGH generation system based on the point source model and proposes the optimization strategy of computing. Then, an optimized calculation formula was proposed to reduce the amount of calculation. Finally, the task debugging was optimized to build a CPU parallel computing system. One of the cores was responsible for startup and function, and data transmission, while the other cores undertook some computing tasks to further improve the computing speed. The results show that, the designed system makes full use of the performance of both CPU and GPU. Under the same configuration of computing hardware, the speedup ratio of CGH generation is 4~4.75 times higher than that of CGH generation in a single GPU system. Heterogeneous systems can effectively improve the generation speed of computer-generated holograms. The research is helpful for generating a 3-D scene hologram quickly.
-
Key words:
- holography /
- computer-generated hologram /
- heterogeneous system /
- point-source model
-
表 1 CPU-GPU异构系统与GPU系统时间对比
Table 1. Time comparison between CPU-GPU heterogeneous system and GPU system
number of points 2354 4708 9416 11770 21174 42348 time spent by CPU-GPU system/ms 347 622 1138 1415 2521 4962 time spent by GPU system/ms 1417 2753 5366 6608 11840 23539 speedup ratio 4.08 4.43 4.72 4.67 4.70 4.74 number of points 101168 202336 404672 1018748 2037496 time spent by CPU-GPU system/ms 11763 23912 47558 120979 242568 time spent by GPU system/ms 56545 113783 227851 575493 1151167 speedup ratio 4.81 4.76 4.79 4.76 4.75 -
[1] SAHIN E, STOYKOVA E, MKINEN J, et al. computer-generated holograms for 3D imaging: A survey[J]. ACM Computing Surveys, 2020, 53(2): 1-35. [2] ATHANASIA S, DAVID B, PETER S. Color computer-generated holography for point clouds utilizing the Phong illumination model[J]. Optics Express, 2018, 26(8): 10282-10298. doi: 10.1364/OE.26.010282 [3] 曾胜财, 甘亮勤. 编码法制彩色动态全息[J]. 激光技术, 2021, 45(2): 229-232. ZENG Sh C, GAN L Q. Making color dynamic holograms by the coding method[J]. Laser Technology, 2021, 45(2): 229-232(in Ch-inese). [4] 刘柳, 姚燕, 蔡晋辉, 等. 基于数字全息的甲烷-氧气预混火焰温度场研究[J]. 激光技术, 2022, 46(3): 408-414. LIU L, YAO Y, CAI J H, et al. Study on methane-oxygen premixed flame temperature field based on digital holography[J]. Laser Technology, 2022, 46(3): 408-414(in Chinese). [5] REN N, KOHEI S, YOSHIKI M. Real-time gradation-expressible amplitude-modulationtype electroholography based on binary-weighted computer-generated hologram[J]. Chinese Optics Letters, 2021, 19(11): 110501. doi: 10.3788/COL202119.110501 [6] 金晓宇, 桂进斌, 刘超, 等. 基于点源模型计算全息图快速生成算法的研究进展[J]. 激光与光电子学进展, 2018, 55(10): 100005. JIN X Y, GUI J B, LIU Ch, et al. Research progress of fast algorithm for cgh generation based on point source model[J]. Laser & Opto-electronics Progress, 2018, 55(10): 100005(in Chinese). [7] ZHAO Y, SHI C X, KWON K C, et al. Optics communications fast calculation method of computer-generated hologram using a depth camera with point cloud gridding[J]. Optics Communications, 2018, 411: 166-169. doi: 10.1016/j.optcom.2017.11.040 [8] MATSUSHIMA K, NAKAHARA S. New techniques for wave-field rendering of polygon-based high-definition CGHs[J]. Proceedings of the SPIE, 2011, 7957: 79571A. doi: 10.1117/12.876362 [9] PAN Y J, WANG Y T, LIU J, et al. Fast polygon-based method for calculating computer-generated holograms in three-dimensional display[J]. Applied Optics, 2013, A52(1): 290-299. [10] KIM S C, KIM E S. Effective generation of digital holograms of three-dimensional objects using a novel look-up table method[J]. Applied Optics, 2008, D47(19): 55-62. [11] JIA J, WANG Y, LIU J, et al. Reducing the memory usage for e-ffective computer-generated hologram calculation using compressed look-up table in full-color holographic display[J]. Applied Optics, 2013, 52(7): 1404-1412. doi: 10.1364/AO.52.001404 [12] SHIMOBABA T, MASUDA N, ITO T. Simple and fast calculation algorithm for computer-generated hologram with wavefront recording plane[J]. Optics Letters, 2009, 34(20): 3133-3135. doi: 10.1364/OL.34.003133 [13] 吴凯. 基于点源调控的视窗全息动态3维显示方法研究[D]. 苏州: 苏州大学, 2020. WU K. Research on dynamic 3D display method of window holography based on point source control[D]. Soochow: Soochow University, 2020(in Chinese). [14] LUCENT E, MARK E. Interactive computation of holograms using a look-up table[J]. Journal of Electronic Imaging, 1993, 2(1): 28-34. doi: 10.1117/12.133376 [15] OKADA N, HIRAI D, ICHIHASHI Y, et al. Special-purpose computer HORN-7 with FPGA technology for phase modulation type electro-holography[C]//International Display Workshops. New York, USA: IEEE, 2012: 1284-1287. [16] TOMOYOSHI S, TOMOYOSHI I, NOBUYUKI M, et al. Fast calculation of computer-generated-hologram on AMD HD5000 series GPU and OpenCL[J]. Optics Express, 2010, 18(10): 9955-9960. doi: 10.1364/OE.18.009955 [17] TAKADA N, SHIMOBABA T, NAKAYAMA H, et al. Fast high-resolution computer-generated hologram computation using multiple graphics processing unit cluster system[J]. Applied Optics, 2012, 51(30): 7303-7307. doi: 10.1364/AO.51.007303 [18] 蒋晓瑜, 丛彬, 裴闯, 等. 一种基于新型查表方法的统一计算设备架构并行计算全息算法[J]. 光学学报, 2015, 35(2): 0209001. JIANG X Y, CONG B, PEI Ch, et al. A parallel algorithm based on a new table lookup method for unified computing device architecture[J]. Acta Optica Sinica, 2015, 35(2): 0209001(in Chinese). [19] PAN Y, XU X, SOLANKI S, et al. Fast CGH computation using S-LUT on GPU[J]. Optics Express, 2009, 17(21): 18543-18555. doi: 10.1364/OE.17.018543 [20] 许可, 王星儿, 范旭浩, 等. 超表面全息术: 从概念到实现[J]. 光电工程, 2022, 49(10): 220183. XU K, WANG X E, FAN X H, et al. Meta-holography: From concept to realization[J]. Opto-Electron Engineering, 2022, 49(10): 220183(in Chinese). [21] AHRENBERG L, BENZIE P, MAGNOR M, et al. Computer gene-rated holography using parallel commodity graphics hardware[J]. Optics Express, 2006, 14(17): 7636-7641. doi: 10.1364/OE.14.007636 [22] TAKADA N, SHIMOBABA T, NAKAYAMA H, et al. Fast high-resolution computer-generated hologram computation using multiple graphics processing unit cluster system[J]. Applied Optics, 2012, 51(30): 7303-7307. doi: 10.1364/AO.51.007303 [23] JIN X Y, GUI J B, JIANG Zh X, et al. Fast calculation of computer generated hologram using multi-core CPUs and GPU system[J]. Proceedings of the SPIE, 2018, 1117: 10818. -


 网站地图
网站地图

 下载:
下载: