-
激光雷达探测技术在军用和民用工程上有广泛的应用,例如激光测距、测速,激光2维、3维成像[1],激光距离多普勒域成像和合成孔径成像[2]等。所以,对于粗糙体目标激光散射特征研究是其不可缺少的关键技术之一[3-5]。研究人员将入射激光假设为平面波[6-7]来进行激光雷达目标成像的探测和识别,主要是利用粗糙面与激光散射特性及机理去探测目标[8-9]。当激光束从粗糙的目标表面反射时,散射回波包含了物体的物理尺寸、轮廓等重要的信息,对目标的识别、跟踪及粗糙表面光学特性的反演具有重要的意义[10]。
在粗糙面散射中,众多学者利用基尔霍夫理论研究了随机粗糙表面散射特性,其中,激光入射在粗糙凸体目标的散射特征是科研人员长期以来关注的研究热点之一。ISHIMARU等人[4, 11]采用双频互相关函数研究随机脉冲波传播和随机粗糙面脉冲波散射的问题。SALAMI等人[12]根据粗糙表面的统计特性,给出了有阴影效应的相干散射强度大于没有阴影效应的散射强度,非相干散射强度的变化与此相反。CHEN等人[5-6]研究脉冲平面波对2维随机粗糙介质表面的散射特性,给出了激光波束散射双频互相关函数的解析表达式。ZHANG等人以粗糙球体和圆柱体[13]为例,推导了任意形状物体在远场中的相干与非相干分量的表达式[14-15]。YANG等人[16]利用目标散射特性计算旋转粗糙凸物体的时间相关函数,给出了旋转圆锥体目标散斑相关函数。LIU等人[7, 17]利用平面波研究了空间锥形目标的激光散射特性,计算了圆锥的相干散射强度,并分析了散射强度随不同参量的变化规律。作者所在团队[18-19]利用高斯波束入射在粗糙椭球体目标上,推导了散射场量二阶统计矩及非相干分量比的表达式。ZHA等人在高斯波束[20]的基础上,研究了在各向异性媒质中圆柱的散射特性,获得了各向异性圆柱的内场以及近场的归一化散射强度分布图[21]。目前,对于高斯分布任意粗糙体目标的理论建模仍以平面波为主[15, 19]。然而,对于平面波入射下粗糙体目标的非相干分量比研究较少,本文中研究了激光波束入射下空间球体和锥体目标的散射特征。
本文中以标量Helmholtz积分方程和粗糙体目标散射理论研究为基础,计算了2维粗糙体目标散射场非相干分量比。针对粗糙球体和圆锥体散射特性,详细分析了粗糙目标非相干分量比的影响因素,为后期计算更复杂粗糙体目标理论建模及散射特性等问题的研究奠定基础。
-
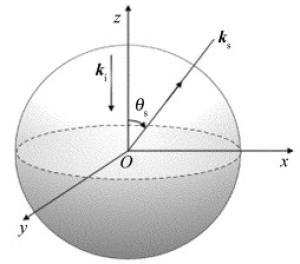
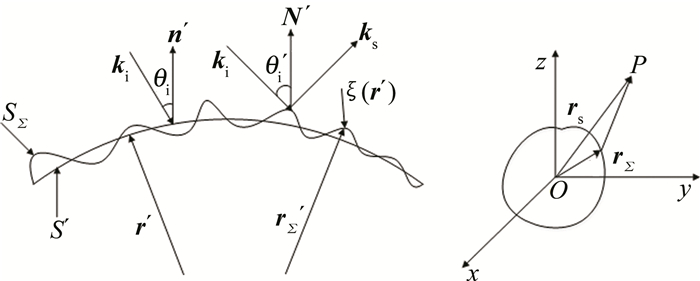
假设入射平面波Ei(r)=exp(ik·r),k=k·$\hat{\boldsymbol{k}}$为波矢,$\hat{\boldsymbol{k}}$表示单位波矢,k=2π/λ为自由空间波数,λ为波长,散射情况如图 1所示。其中,S′是粗糙目标的平均面,SΣ是凸体目标的起伏表面,下标Σ表示起伏;rs为观察点P与目标坐标系原点之间的矢量距离,rΣ′为目标原点到面SΣ的矢径;r′为目标原点到面S′的矢径;n′为平均面S′的单位外法向矢量,N′为起伏表面SΣ的外法向矢量,ξ(r′)是沿光滑面S′外法线方向的随机高度起伏,且为高斯零均值分布;θi为r′位置的局部入射角,θi′为rΣ′位置的入射角;ki是入射波矢,ks是散射矢量。为了计算过程方便,省略入射波的时间因子exp(-iωt)。
Figure 1. Schematic diagram of scattering of rough objects[6]
根据标量Helmholtz方程[6],散射场表达式为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\int_{S_{\varSigma}}\left[E\left(\boldsymbol{r}_{\varSigma}^{\prime}\right) \frac{\partial G\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}-\right. \\ \left.G\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}_{\varSigma}^{\prime}\right) \frac{\partial E\left(\boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}\right] \mathrm{d} S_{\varSigma} \end{gathered} $
(1) 式中,$E\left(\boldsymbol{r}_{\varSigma}^{\prime}\right) \text { 和 } \frac{\partial E\left(\boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}$为粗糙面SΣ上的总电场和它的法向导数; G(rs, rΣ′)为自由空间标量格林函数,其表达式为:
$ G\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}_{\varSigma}^{\prime}\right)=\frac{\exp \left[\mathrm{i} k\left(\left|\boldsymbol{r}_s-\boldsymbol{r}_{\varSigma}^{\prime}\right|\right)\right]}{4 \pi\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}_{\varSigma}^{\prime}\right|} $
(2) 观察点P处的散射场表达式为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\int_{S_{\varSigma}}\left[E^{\prime}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right) \frac{\partial G\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}-\right. \\ \left.G\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}_{\varSigma}^{\prime}\right) \frac{\partial E^{\prime}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}\right] \mathrm{d} S_{\varSigma} \end{gathered} $
(3) 当表面任一点的主曲率半径远大于入射波长,可采用切平面近似。粗糙面上任一点rΣ′上的散射场和法向导数可分别为:
$ E^{\prime}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right)=\left(1+R_{\mathrm{i}}\right) E_{\mathrm{i}}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right) $
(4) $ \frac{\partial E^{\prime}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right)}{\partial \boldsymbol{N}^{\prime}}=\mathrm{i}\left(1-R_{\mathrm{i}}\right) \boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{N}^{\prime} E_{\mathrm{i}}\left(\boldsymbol{r}_{\varSigma}^{\prime}\right) $
(5) 式中,Ri为菲涅耳反射系数。采用远场近似,(1)式可简化为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\frac{\mathrm{i}}{4 \pi} \int_{S_{\varSigma}}\left\{\left(\boldsymbol{R}_{\mathrm{i}} \boldsymbol{V}-\boldsymbol{M}\right) \cdot \boldsymbol{N}^{\prime} \exp \left(\mathrm{i} \boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right. \\ \left.\frac{\exp \left[\mathrm{i} k\left(\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}_{\varSigma}^{\prime}\right|\right)\right]}{\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}_{\varSigma}^{\prime}\right|}\right\} \mathrm{d} S_{\varSigma} \end{gathered} $
(6) 式中,令$\boldsymbol{V}=\boldsymbol{k}_{\mathrm{i}}-\boldsymbol{k}_{\mathrm{s}}, \boldsymbol{M}=\boldsymbol{k}_{\mathrm{i}}+\boldsymbol{k}_{\mathrm{s}}$, 则: $\boldsymbol{k}_{\mathrm{i}}=k\left(\sin \theta_{\mathrm{i}} \cos \varphi_{\mathrm{i}}, \right.\left.\sin \theta_{\mathrm{i}} \sin \varphi_{\mathrm{i}}, -\cos \theta_{\mathrm{i}}\right)$, $\boldsymbol{k}_{\mathrm{s}}=k\left(\sin \theta_{\mathrm{s}} \cos \varphi_{\mathrm{s}}, \sin \theta_{\mathrm{s}} \sin \varphi_{\mathrm{s}}, \right.\left.\cos \theta_{\mathrm{s}}\right)$。
假设目标为导体,粗糙目标的远场散射场可简化为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\frac{-\mathrm{i}}{2 \pi} \int_{S^{\prime}}\left\{\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}^{\prime} \exp \left[\mathrm{i} \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right] \times\right. \\ \left.\frac{\exp \left[\mathrm{i}\left(k\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right|+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right]}{\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right|}\right\} \mathrm{d} S^{\prime} \end{gathered} $
(7) 利用远场近似,(7)式中距离为:
$ \left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right| \approx \boldsymbol{R}-\frac{\boldsymbol{r}^{\prime} \cdot \boldsymbol{r}_{\mathrm{s}}}{k} $
(8) (7) 式中指数项的分母|rs-r′|可以近似为R,R是观察点P与光滑面S′原点之间的距离,则粗糙目标的远区散射场可表示为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\frac{-\operatorname{iexp}(\mathrm{i} k \boldsymbol{R})}{2 \pi \boldsymbol{R}} \int_{S^{\prime}} \boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}^{\prime} \exp \left[\mathrm{i} \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right] \times \\ \exp \left(\mathrm{i} \boldsymbol{V} \cdot \boldsymbol{r}^{\prime}\right) \mathrm{d} S^{\prime} \end{gathered} $
(9) -
根据(9)式可知,平均散射场可表示为:
$ \begin{gathered} \left\langle E_{\mathrm{s}}\right\rangle=\frac{-\operatorname{iexp}(\mathrm{i} k \boldsymbol{R})}{2 \pi \boldsymbol{R}} \int_{S^{\prime}} \boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}^{\prime}\left\langle\exp \left[\mathrm{i} \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right]\right\rangle \times \\ \exp \left(\mathrm{i} \boldsymbol{V} \cdot \boldsymbol{r}^{\prime}\right) \mathrm{d} S^{\prime} \end{gathered} $
(10) 散射场场量的二阶统计特征即互相关函数表达式[15]为:
$ \begin{gathered} I_{\mathrm{c}}=\left\langle E_{\mathrm{s}}\right\rangle\left\langle E_{\mathrm{s}}{ }^*\right\rangle=\frac{\exp \left[\mathrm{i}\left(k_1-k_2\right) \boldsymbol{R}\right]}{(2 \pi \boldsymbol{R})^2} \times \\ \int_{S^{\prime}} \mathrm{d} \boldsymbol{r}_1{ }^{\prime} \int_{S^{\prime \prime}} \mathrm{d} \boldsymbol{r}_2{ }^{\prime}\left(\boldsymbol{k}_{\mathrm{i}, 1} \cdot \boldsymbol{n}_1{ }^{\prime}\right)\left(\boldsymbol{k}_{\mathrm{i}, 2} \cdot \boldsymbol{n}_2{ }^{\prime}\right) \times \\ \quad \exp \left[\mathrm{i} \boldsymbol{V}\left(\boldsymbol{r}_1{ }^{\prime}-\boldsymbol{r}_2{ }^{\prime}\right)\right] \times \\ \left\langle\exp \left[\mathrm{i} \boldsymbol{V} \boldsymbol{n}_1{ }^{\prime} \xi\left(\boldsymbol{r}_1{ }^{\prime}\right)\right]\right\rangle\left\langle\exp \left[-\mathrm{i} \boldsymbol{V} \boldsymbol{n}_2{ }^{\prime} \xi\left(\boldsymbol{r}_2{ }^{\prime}\right)\right]\right\rangle \end{gathered} $
(11) 式中, r1′为目标原点到光滑面S′的矢径,r2′为目标原点到光滑面S″的矢径,S″是粗糙目标散射场共轭后的光滑面,k1为散射场Es的自由空间波数,k2为散射场Es共轭后的自由空间波数,ki, 1表示散射场Es的入射波数矢量,n1′为光滑面S′的单位外法向矢量,ki, 2表示散射场Es共轭后的入射波数矢量,n2′为光滑面S″的单位外法向矢量,ξ(r1′)是沿光滑面S′外法线方向的随机高度起伏,ξ(r2′)是沿光滑面S″外法线方向的随机高度起伏。
散射场量强度的非相干分量可表示为:
$ I_{\mathrm{f}}=\left\langle E_{\mathrm{s}} E_{\mathrm{s}}^*\right\rangle-\left|\left\langle E_{\mathrm{s}}\right\rangle\right|^2=K \int_{\mathrm{S}^{\prime}} \mathrm{d} \boldsymbol{r}_1{ }^{\prime} \int_{S^{\prime \prime}} \mathrm{d} \boldsymbol{r}_2{ }^{\prime}\left(\boldsymbol{k}_{i, 1} \cdot \boldsymbol{n}_1{ }^{\prime}\right) \times \\ \begin{gathered} \left(\boldsymbol{k}_{\mathrm{i}, 2} \cdot \boldsymbol{n}_2{ }^{\prime}\right) \exp \left[\mathrm{i} \boldsymbol{V}\left(\boldsymbol{r}_1{ }^{\prime}-\boldsymbol{r}_2{ }^{\prime}\right)\right] \times \\ \left(\chi_{\mathrm{f}}-\chi_1 \chi_2\right) \end{gathered} $
(12) 式中, $K=\exp \left[\mathrm{i}\left(k_1-k_2\right) \boldsymbol{R}\right] /(2 \pi \boldsymbol{R})^2$,粗糙面起伏函数ξ(r′)服从高斯分布,粗糙面的粗糙度为σ,相关长度为lc,令Vz=V·n′,则高斯分布的1阶、2阶特征函数[14]分别为χ1=exp(-k12σ2Vz2/2), χ2=exp(-k22σ2Vz2/2), χf=exp[-k2σ2Vz2(1-〈ξ1ξ2〉)]。
定义比值系数γ12为:
$ \gamma_{12}=\frac{I_{\mathrm{f}}}{I_{\mathrm{c}}} $
(13) 由(11)式、(12)式可定义γ12的数学含义,其为高斯粗糙球体非相干分量与相干分量的比值。如图 2所示,入射平面波沿着-z轴方向入射在粗糙球体上,球体中心位于坐标系的原点。假设平面波入射波长λ=1.06μm,球体半径为a,σ为粗糙面的粗糙度,lc为相关长度,入射角θi=0°,方位角φi=0°,其轴线与ks的夹角为θs,即ks=(sinθs, 0, cosθs)。
-
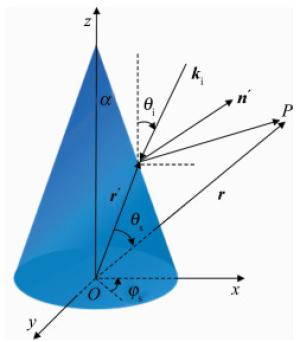
假设平面波入射在圆锥体侧面,取圆锥底面中心为坐标原点,如图 3所示,圆锥体的底面半径为b,高为h,半锥角为α,方位角为φ,则锥面方程[7]为:
$ \left\{\begin{array}{l} x=(h-z) \tan \alpha \cos \varphi \\ y=(h-z) \tan \alpha \sin \varphi \\ z=z \end{array}\right. $
(14) 则圆锥曲面上的微元$\mathrm{d} s=(h-z) \tan \alpha \cdot \sec \alpha \mathrm{d} \varphi \mathrm{d} z$。假设入射波在平面xOz内,即方位角为0°。圆锥的散射波矢量为$\boldsymbol{k}_{\mathrm{s}}=\sin \theta_{\mathrm{s}}\left(\cos \varphi_{\mathrm{s}} \cdot \boldsymbol{x}+\sin \varphi_{\mathrm{s}} \cdot \boldsymbol{y}\right)+\cos \theta_{\mathrm{s}} \cdot \boldsymbol{z}$,法向矢量为$\boldsymbol{n}^{\prime}=\cos \alpha \cos \varphi \cdot \boldsymbol{x}+\cos \alpha \sin \varphi \cdot \boldsymbol{y}+\sin \alpha \cdot \boldsymbol{z}$,入射波矢量为$\boldsymbol{k}_{\mathrm{i}}=-\sin \theta_{\mathrm{i}} \cdot \boldsymbol{x}-\cos \theta_{\mathrm{i}} \cdot \boldsymbol{z}, \boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}$分别为单位正交基向量。
由$\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right| \approx\left|\boldsymbol{r}_{\mathrm{s}}\right|-\left|\boldsymbol{r}^{\prime}\right| \cdot \cos \left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime}\right)$可知,在稳相点处有$\tan \varphi=\sin \theta_{\mathrm{s}} \sin \varphi_{\mathrm{s}} /\left(\sin \theta_{\mathrm{s}} \cos \varphi_{\mathrm{s}}+\sin \theta_{\mathrm{i}}\right)$,在高频极限条件下,$\boldsymbol{k}_{\mathrm{s}} \cdot \boldsymbol{n}^{\prime}=-\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}^{\prime}=\cos \theta_0$,即$\cos ^2 \theta_0=\frac{\left(1-\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{k}_{\mathrm{s}}\right)}{2}, \theta_0$为镜向点处的入射角,则粗糙圆锥体的散射场为:
$ \begin{gathered} E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)=\frac{-\mathrm{i}}{2 \pi} \int_{S^{\prime}} R_{\mathrm{i}} \cos \theta_0 \exp \left[\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right] \times \\ \frac{\exp \left[\mathrm{i}\left(k\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right|+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right]}{\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right|} \mathrm{d} S^{\prime} \end{gathered} $
(15) 令$\boldsymbol{R}\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime}\right)=\left|\boldsymbol{r}_{\mathrm{s}}-\boldsymbol{r}^{\prime}\right|, \boldsymbol{R}$是观察点P与光滑面S′原点之间的距离,则平均散射场可表示为:
$ \begin{aligned} & \left\langle E_{\mathrm{s}}\left(\boldsymbol{r}_{\mathrm{s}}\right)\right\rangle=\frac{-\mathrm{i} R_{\mathrm{i}} \cos \theta_0 \tan \alpha \sec \alpha}{2 \pi}\langle\exp [\mathrm{i} k \boldsymbol{V} \cdot \\ & \left.\left.\boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right]\right\rangle \int_0^h(h-z) \frac{\exp \left[\mathrm{i}\left(k \boldsymbol{R}+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right]}{\boldsymbol{R}} \mathrm{d} z \end{aligned} $
(16) 利用高频近似,则(16)式的积分可简化为:
$ \begin{gathered} \int_0^h(h-z) \frac{\exp \left[\mathrm{i}\left(k \boldsymbol{R}+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right]}{\boldsymbol{R}} \mathrm{d} z=-\frac{\exp \left\{\mathrm{i} k \boldsymbol{R}-\mathrm{i} k a\left[\sin \theta_{\mathrm{s}} \cos \left(\varphi-\varphi_{\mathrm{s}}\right)+\sin \theta_{\mathrm{i}} \cos \varphi\right]\right\}}{\mathrm{i} \boldsymbol{R} k\left\{\tan \alpha\left[\sin \theta_{\mathrm{s}} \cos \left(\varphi-\varphi_{\mathrm{s}}\right)+\sin \theta_{\mathrm{i}} \cos \varphi\right]-\cos \theta_{\mathrm{s}}-\cos \theta_{\mathrm{i}}\right\}} \times \\ \left\{h \cdot \exp \left[\mathrm{i} k h\left[\tan \alpha\left[\sin \theta_{\mathrm{s}} \cos \left(\varphi-\varphi_{\mathrm{s}}\right)+\sin \theta_{\mathrm{i}} \cos \varphi\right]-\cos \theta_{\mathrm{s}}-\cos \theta_{\mathrm{i}}\right]\right]\right\} \end{gathered} $
(17) 故锥体目标的相干散射分量为:
$ I_{\mathrm{c}}=\left|\left\langle E_{\mathrm{s}}\right\rangle^2\right| $
(18) 根据粗糙面散射理论及(15)式、(16)式,粗糙圆锥体对平面波的非相干散射分量为:
$ \begin{aligned} & I_{\mathrm{f}}=\left\langle E_{\mathrm{s}} E_{\mathrm{s}}^*\right\rangle-\left|\left\langle E_{\mathrm{s}}\right\rangle\right|^2= \\ & \frac{1}{4 \pi} \int_{S^{\prime}} \int_{S^{\prime \prime}} \frac{\left|R_{\mathrm{i}}\right|^2 \cos ^2 \theta_0 \exp \left[\mathrm{i}\left(k \boldsymbol{R}\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime}\right)+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime}\right)\right]}{\boldsymbol{R}\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime}\right) \boldsymbol{R}\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime \prime}\right)} \times \\ & \exp \left[\mathrm{i}\left(k \boldsymbol{R}\left(\boldsymbol{r}_{\mathrm{s}}, \boldsymbol{r}^{\prime \prime}\right)+\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{r}^{\prime \prime}\right)\right] \times \\ & \left\{\left\langle\exp \left[\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)-\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime \prime} \xi\left(\boldsymbol{r}^{\prime \prime}\right)\right]\right\rangle-\right. \\ & \left\langle\exp \left[\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right]\right\rangle \times \\ & \left\langle\exp \left[\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime \prime} \xi\left(\boldsymbol{r}^{\prime \prime}\right)\right]\right\} \mathrm{d} S^{\prime} \mathrm{d} S^{\prime \prime} \end{aligned} $
(19) 由图 4可知,引入新的积分变量,假设S′面上任一点处的曲率半径近似等于圆锥体底面半径b,且曲率半径远大于波长λ和粗糙面的相关长度lc,并满足条件Vlc2/a≪1,则V·n′≈V·n″,对dR的积分可以远近似用在r′处的切平面S⊥′(r′)内的积分代替,即积分变量dR≈dR⊥。
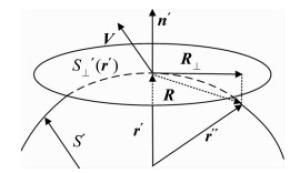
Figure 4. Tangential plane approximate calculation of the incoherent scattering intensity of the object[7]
当观察点位于散射场远场时,令ρ(rs, r′)≈R(rs, r′)+ki·r′,将(19)式进一步简化为:
$ \begin{aligned} I_{\mathrm{f}} & =\frac{\left|\boldsymbol{R}_{\mathrm{i}}\right|^2 \cos ^2 \theta_0}{4 \pi} \int_{S^{\prime}} \mathrm{d} S^{\prime} \int_{S^{\prime \prime}} \frac{\exp (\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{R})}{\rho^2\left(\boldsymbol{r}_{\mathrm{s}}\right)} \cdot \\ & {\left[\chi_2\left(\boldsymbol{V} \cdot \boldsymbol{n}^{\prime} ; \boldsymbol{R}_{\perp}\right)-\chi^2\left(\boldsymbol{V} \cdot \boldsymbol{n}^{\prime}\right)\right] \mathrm{d} \boldsymbol{R}_{\perp} } \end{aligned} $
(20) 式中,$\chi_2\left(\boldsymbol{V} \cdot \boldsymbol{n}^{\prime} ; \boldsymbol{R}_{\perp}\right)=\left\langle\operatorname { e x p } \left\{\mathrm { i } k \boldsymbol { V } \cdot \boldsymbol { n } ^ { \prime } \left[\xi\left(\boldsymbol{r}^{\prime}\right)-\xi\left(\boldsymbol{r}^{\prime}+\right.\right.\right.\right.\left.\left.\left.\left.\boldsymbol{R}_{\perp}\right)\right]\right\}\right\rangle, \chi\left(\boldsymbol{V} \cdot \boldsymbol{n}^{\prime}\right)=\left\langle\exp \left[\mathrm{i} k \boldsymbol{V} \cdot \boldsymbol{n}^{\prime} \xi\left(\boldsymbol{r}^{\prime}\right)\right]\right\rangle$为1维、2维特征函数。
根据ISHIMARU[4]的描述,平面波对粗糙物体的非相干散射强度可以看作是平面波入射场的单位面积粗糙平面非相干射强度的叠加,则:
$ I_{\mathrm{f}}=A \cdot I_{\mathrm{f}, 0} $
(21) 式中, A=(2L)2为被照射面积,If, 0为单位面积粗糙面的非相干散射强度。
对于圆锥的非相干散射有:
$ I_{\mathrm{f}}=\int_{S^{\prime}} I_{\mathrm{f}, 0} S\left(\theta_{\mathrm{i}}, \theta_{\mathrm{s}}\right) \mathrm{d} S^{\prime} $
(22) 式中, S(θi, θs)为遮蔽函数,且:
$ \begin{gathered} S\left(\theta_{\mathrm{i}}, \theta_{\mathrm{s}}\right)=S\left(\theta_{\mathrm{i}}\right) S\left(\theta_{\mathrm{s}}\right)= \\ \left\{\begin{array}{l} 1, \left(-\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}_{\mathrm{s}}>0 \text { 且 } \boldsymbol{k}_{\mathrm{s}} \cdot \boldsymbol{n}_{\mathrm{s}}>0\right) \\ 0, \left(-\boldsymbol{k}_{\mathrm{i}} \cdot \boldsymbol{n}_{\mathrm{s}}<0 \text { 或 } \boldsymbol{k}_{\mathrm{s}} \cdot \boldsymbol{n}_{\mathrm{s}}<0\right) \end{array}\right. \end{gathered} $
(23) (23) 式表示曲面积分只在照射区域进行。If, 0为单位面积粗糙平面的非相干散射强度,ns为粗糙物体平均表面外法向单位矢量。将(17)式代入(20)式得:
$ I_{\mathrm{f}}=\frac{h^2}{2} \tan \alpha \sec \alpha \int I_{\mathrm{f}, 0} S\left(\theta_{\mathrm{i}}, \theta_{\mathrm{s}}\right) \mathrm{d} \varphi $
(24) 由(18)式、(20)式和(24)式可计算出粗糙圆锥体目标的非相干散射分量比。
-
计算结果表明,由图 5a中给出3种不同高度起伏条件下对应的γ12值可以发现,粗糙度越大,非相干分量越多,相干分量越少,球体表面越粗糙;由图 5b可以看出,球体半径a对非相干分量比的影响较大,在散射角为45°时存在峰值,且随着球体半径a的变大,峰值高度变小,相干分量越多,即表面越光滑,该结论同参考文献[19]中的所述相符。
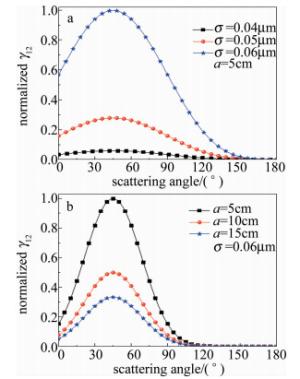
Figure 5. Normalized incoherent component ratio of rough sphere scattering as a function of scattering angle
图 6中给出不同粗糙度条件下,粗糙球体散射归一化非相干分量比随相关长度的变化情况。从图中可以看出, 当粗糙度增大时,对应曲线上升的速度越快,即非相干分量占总分量的比重越大。由图 7可以发现, 当粗糙度增加时, 球体半径a不同对非相干分量比有影响,且随着球体半径a增加,球体非相干分量比逐渐变小。
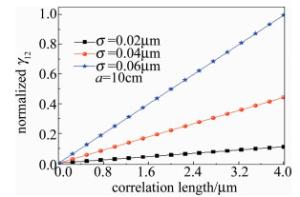
Figure 6. Normalized incoherent component ratio of rough sphere scattering varies with correlation length
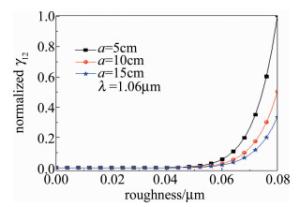
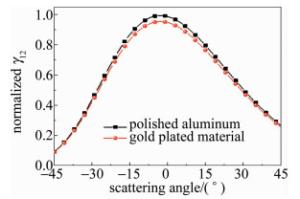
假设圆锥的计算波长λ=1.06μm,圆锥体底面半径b=1m,半锥角α=15°,入射光与z轴的夹角θi=30°,抛光铝材料的复折射率为2.43+10.7i,镀金包覆薄膜材料的复折射率为1.2277+10.3768i,观察方位角φs=30°,粗糙度分别为σ=0.05μm, σ=0.1μm和σ=0.2μm。
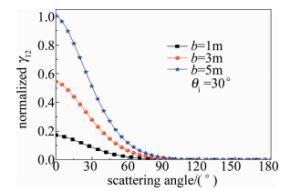
图 8中给出了粗糙圆锥体目标随散射角的变化情况。可以发现,粗糙度对非相干分量比有很大影响,随着粗糙度的不同,非相干分量比的峰值位置也有所不同,但均位于镜反射方向上。图 9中给出圆锥体的底面半径b越大,非相干分量比就越大,函数γ12的下降速度就越快。
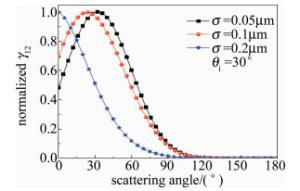
Figure 8. Variation of normalized incoherent component ratio of cone scattering under different roughness
图 10中给出了两种不同目标材料随散射角的变化情况。由图可看出,抛光铝材料圆锥体非相干分量比大于镀金包覆薄膜材料。由图 11可以看出,不同的粗糙度下,随着圆锥入射角的增加,函数γ12的峰值位置发生变化,与图 8中的变化趋势相似。图中结论与参考文献[19]和参考文献[7]中所述结论相符。
-
基于物理光学近似,在平面波激光照射下,从理论上研究2维高斯分布粗糙体目标的远区散射场及双频互相关函数。以粗糙球体和圆锥体目标为例,通过数值方法分析了球体、圆锥体散射的非相干分量比随散射角、粗糙度、半径及目标材料等因素的变化情况。
(1) 散射角对粗糙球体散射的非相干分量比有影响,当粗糙度越大,目标非相干散射分量在总散射分量中的比重较大,且与参考文献[18]中的结论相符。
(2) 粗糙球体半径a变大,非相干分量比变小,相干分量越大。
(3) 粗糙度的不同对圆锥体目标散射的非相干分量比的峰值位置有影响,且峰值均位于镜反射方向上。
(4) 圆锥体的底面半径b变化与非相干分量比成正比,对于不同的目标材料,可以发现抛光铝材料的非相干分量比大于镀金包覆薄膜材料。
综上所述,研究高斯粗糙面散射特性实质上是采用定量方法讨论各种粗糙体目标的非相干分量比受哪些因素影响。通过研究粗糙体目标的散射特性,对开展更复杂的目标激光散射统计特性、以及激光散斑探测和识别等问题提供了理论依据。
粗糙球体和锥体目标激光散射非相干分量比
Incoherent component ratio of laser scattering from rough sphere and cone targets
-
摘要: 为了研究激光散斑对目标探测的影响,采用物理光学近似方法,进行了平面波激光照射在粗糙球体和圆锥体目标时对散射场统计特性的理论分析,推导了粗糙体目标散射场量的二阶统计矩, 数值计算了粗糙球体和锥体的非相干散射分量比随粗糙度、散射角、半径及目标材料的变化情况。结果表明,散射角的变化对粗糙球体散射非相干分量比有影响,粗糙度变大,目标的非相干分量占总散射分量的比重越大;随着粗糙球体半径变小,球体表面越粗糙;圆锥体目标散射非相干分量比的峰值位置随粗糙度变化而不同,但其峰值均位于镜反射方向上;金属类材料比非金属抛光铝材料的非相干分量比小,且半径变化与非相干分量比成正比。该研究结果可为更复杂目标激光散射特性和激光散斑探测、识别的研究提供一定的参考价值。Abstract: In order to study the effect of laser speckle on target detection, the theoretical analysis of the statistical characteristics of the scattering field when the plane wave laser irradiates the rough sphere and cone target was carried out by using the physical optics approximation method, and the second order statistical moment of the scattering field quantity of rough targets was derived. The variation of incoherent scattering component ratio of rough sphere and cone with roughness, scattering angle, radius, and target material is calculated numerically. The results show that the change of scattering angle has an effect on the incoherent component ratio of rough sphere scattering. The larger the roughness, the larger the proportion of incoherent component of target to the total scattering component. As the radius of the rough sphere becomes smaller, the surface of the sphere becomes rougher. The peak position of incoherent component ratio of cone target scattering varies with roughness, but its peaks are all located in the direction of specular reflection. The incoherent component ratio of metallic materials is smaller than that of non-metallic polished aluminum materials, and the radius change is proportional to the incoherent component ratio. The research results provide some reference value for the study of laser scattering characteristics of more complex targets and laser speckle detection and identification.
-
Figure 1. Schematic diagram of scattering of rough objects[6]
Figure 4. Tangential plane approximate calculation of the incoherent scattering intensity of the object[7]
-
[1] WANG M J. Research on scatter of pulse beam by target with rough surface and its laser range Doppler imaging[D]. Xi'an: Xidian University, 2008: 83-96(in Chinese). [2] DANG W J, ZENG X D, CAO Ch Q, et al. Simulation of the rough target's signal in synthetic aperture ladar[J]. Acta Photonica Sinica, 2015, 44(3): 304001(in Chinese). doi: 10.3788/gzxb20154403.0304001 [3] OGILVY J A. Wave scattering from rough surfaces[J]. Reports on Progress in Physics, 1987, 50(12): 1553-1608. doi: 10.1088/0034-4885/50/12/001 [4] ISHIMARU A. Wave propagation and scattering in random media[M]. New York, USA: Academic Press, 1978: 116-148. [5] CHEN H, WU Zh S, BAI L. Research on the coherent scattering of Gaussian beam from arbitrarily shaped convex object with rough surface[J]. Acta Optical Sinica, 2005, 25(1): 115-120(in Chinese). [6] CHEN H. Scattering of Gaussian beam by object with rough surface and its application on laser one-dimensional range profile[D]. Xi'an: Xidian University, 2004: 35-38(in Chinese). [7] CHEN H B. Study on light scattering characteristics of random rough cone surface[D]. Chengdu: University of Electronic Science and Technology of China, 2006: 35-44(in Chinese). [8] WANG M J, WU Zh S, LI Y L, et al. Research progress on the laser range-resolved Doppler imaging radar and its key technologies[J]. Laser & Infrared, 2009, 39(5): 464-467(in Chinese). doi: 10.3969/j.issn.1001-5078.2009.05.002 [9] COLLIN R E. Scattering of an incident Gaussian beam by a perfectly conducting rough surface[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(1): 70- 74. doi: 10.1109/8.272303 [10] WHITMAN G M, WANG Q I, SPECTOR P, et al. Gaussian beam scattering from a deterministic rough metal surface[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(5): 1868-1876. doi: 10.1109/TAP.2016.2537383 [11] ISHIMARU A, AILES-SENGERS L, PHU P, et al. Pulse broadening and two-frequency mutual coherence function of the scattered wave from rough surfaces[J]. Waves in Random Media, 1994, 4(2): 139-148. doi: 10.1088/0959-7174/4/2/004 [12] SALAMI M, HAJIAN A, FAZELI S M, et al. How shadows shape our impression of rough surfaces[J]. Journal of Applied Physics, 2014, 116(24): 243502. doi: 10.1063/1.4904409 [13] WU Y L, WU Zh S, ZHANG G. Study of anisotropic speckle pa-tterns by rough cylindrical surfaces[J]. Journal of Applied Optics, 2011, 32(1): 35-39(in Chinese). [14] ZHANG G, WU Zh S. Two-frequency mutual coherence function of scattering from arbitrarily shaped rough objects[J]. Optics Express, 2011, 19(8): 7007-7019. doi: 10.1364/OE.19.007007 [15] ZHANG G. Statistical properties of laser speckle from rough objects and analysis on micro-motion characteristic[D]. Xi'an: Xidian University, 2013: 28-27(in Chinese). [16] YANG Zh Q, WU Zh S, ZHANG G, et al. Recognition technology for obtaining micro-motion characteristics of rotating rough targets[J]. Acta Physica Sinica, 2014, 63(21): 210301(in Chinese). doi: 10.7498/aps.63.210301 [17] LIU J B. Light scattering of cone-shaped space objects by using small perturbation approximate[J]. Acta Photonica Sinica, 2009, 38(10): 2665-2668(in Chinese). [18] WANG M J, KE X Zh, LI Y L, et al. Statistical moment and incoherent component ratio of laser beam scattering from targets with arbitrary shapes[J]. Acta Optical Sinica, 2016, 36(7): 0729001 (in Chinese). doi: 10.3788/AOS201636.0729001 [19] YAN K D, FU Y Sh, YU X N, et al. Numerical study on gaussian and exponential light scattering from randomly rough surfaces[J]. Computer & Digital Engineering, 2018, 46(4): 644-648(in Chin-ese). [20] YE D H. Analysis and application of gauss beam characteristics[J]. Laser Technology, 2019, 43(1): 142-146 (in Chinese). [21] ZHA X M, ZHU D. Scattering characteristics of Hermite-Gaussian beam on anisotropic cylinder[J]. Laser Technology, 2020, 44(3): 338(in Chinese). -


 网站地图
网站地图

 下载:
下载: