-
激光雷达近年来在3-D场景感知及重建方面得到了广泛的应用,例如地形勘探、遗迹保护、城市建模、智能驾驶以及电力巡线等[1-6],由激光雷达扫描获取的3-D点云数据经过点云滤波、特征点匹配、点云配准等步骤后获得, 用于还原3-D场景[7-9]。点云配准是3维场景重建中至关重要的环节,配准方法可分为:手动配准、依赖于仪器的配准以及自动配准[10]。由于场景重建所需要的数据量较大,点云数量较多,手动配准与依赖于仪器的配准效率太低,一般采用自动配准方法[11]。自动配准方法所使用的算法不同,如何优化配准时间与精度成为了点云配准的主要研究方向。
最经典的点云配准方法是由BESL和McKAY提出的最近迭代点(iterative closest point, ICP)算法[12],它能精度较高地实现点云配准,但计算量大,对点云数据的初始条件要求较高,且容易陷入局部最优。在ICP算法的基础上,众多学者对ICP算法进行了改进:BOUAZIZ等人提出的稀疏ICP(sparse iterative closest point, SICP)算法[13],削弱了离群点对配准效果的影响,提高了配准精度;RUSINKIEWICZ等人提出利用点-面对应来代替点-点对应[14],可以大大提高算法的稳健性和收敛精度。在优化算法方面,WU等人尝试使用二进制编码的标准遗传算法(standard genetic algorithm, SGA)进行配准, 但这一算法搜索空间大, 匹配时间长[15];DUAN等人使用粒子群优化算法寻找对应点后使用ICP算法实现散乱点云配准[16],速度较快但易陷入局部最优。
现阶段点云自动配准方法多数采用寻找特征点的方式进行匹配,优化特征点间的对应关系来实现点云配准,此方法计算量较大且仅在特征点较明显的场景下可以获得较好的结果。在优化算法层面,粒子群算法(particle swarm optimization, PSO)搜索速度快、效率高,算法简单,但对于离散优化问题处理效率不高,容易陷入局部最优[17]。天牛须搜索算法(beetle antennae search, BAS)在全局搜索最优解方面具有优势,可弥补粒子群算法易陷入局部最优的问题[18]。为解决以上问题提出一种基于天牛须改进的粒子群算法(particle swarm optimization algorithm improved by beetle antennae algorithm, BAS-PSO),以优化点云分布熵(spatial distribution entropy, SDE)为目标,寻找能够使点云分布熵最小的空间坐标变化关系,对于任意未知对应关系的两组点云数据,获得其旋转矩阵以实现点云粗配准,为精配准提供良好的初始值。
-
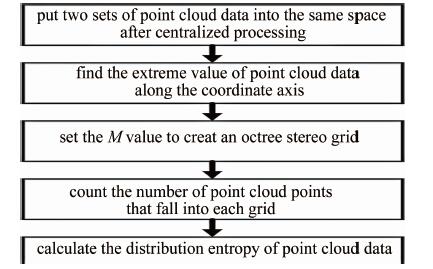
本文中使用八叉树建立3-D立方栅格。将初始两组点云数据放至同一空间中, 对两组点云数据分别进行中心化处理,将质心移至坐标原点后对合成的点云数据建立3-D立方栅格。由于每个栅格大小一致,而包含在栅格中的点云数量不同,即可通过同一栅格中点云数量的大小来表示在该区域内点云的稀疏程度, 点云数量大表明该区域点云密集,数量小则表明该区域点云稀疏。
点云分布熵可用于描述点云在空间中的位置关系,通过密集程度反映点云的分布情况[19]。点云数据的采集往往是在不同视角的条件下进行的,点云数据之间并没有明显的对应关系[20],在经历配准操作后,点云数据会相对集中而非表现出配准前的不确定状态,这表现在两组点云数据相对距离最小,且空间中的位置关系唯一。点云信息熵可准确反映两组点云在配准过程中位置变换关系,故适用于点云配准过程中的优化对象。求解点云分布熵的具体步骤如图 1所示。
在点云空间中,按照栅格数量切分,将同一空间下的两个点云数据切分为2M×2M×2M个栅格,即每个栅格的大小为:
$ \left\{ \begin{array}{l} x = ({X_{{\rm{max}}}} - {X_{{\rm{min}}}})/{2^M}\\ y = ({Y_{{\rm{max}}}} - {Y_{{\rm{min}}}})/{2^M}\\ z = ({Z_{{\rm{max}}}} - {Z_{{\rm{min}}}})/{2^M}\; \end{array} \right. $
(1) 式中, Xmax, Ymax, Zmax为点云数据坐标轴方向的最大值,Xmin, Ymin, Zmin为最小值,x, y, z为每一个立体栅格沿坐标轴方向的长度。
将点云数据按照边界以及栅格数量进行栅格化后,统计落入每一个栅格中点云数量n(i, j, k),求得其分布概率p(i, j, k):
$ {\rm{ }}p\left( {i, j, k} \right) = n\left( {i, j, k} \right)/N\; $
(2) 式中,N为两组点云的总点云数量。点云分布熵的表达形式为:
$ {E_{{\rm{SDE}}}} = \sum\limits_i^{{2^M}} {\sum\limits_j^{{2^M}} {\sum\limits_k^{{2^M}} {p\left( {i, j, k} \right){\rm{ln}}[p(i, j, k)]} } } $
(3) 相比ICP算法通过求算均值平方差(mean square error, MSE)来评价点云配准的精度,点云分布熵的求算方式时间复杂度更小。MSE的求算方法需要为待配准点云中每一个点在目标点云中找寻与之距离最小的点,这需要多次全局遍历,而点云分布熵的评价方式只需进行一次遍历,运算速度有较大提高。
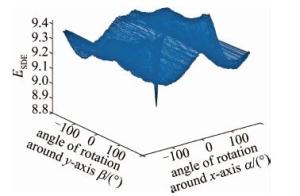
对完全重合的两组bunny点云数据P, Q进行点云分布熵计算操作。在-180°~180°范围内将Q绕x轴旋转, 每1°生成一个新的点云数据Qm,Qm与P共同组成新的点云数据Tm,计算Tm的点云分布熵ESDE和均值平方差EMSE。下标m表示旋转角α, β, γ的角度。以旋转角度α为横坐标,ESDE与EMSE为纵坐标建立与旋转角度的对应关系,如图 2所示。Q绕x轴与y轴旋转计算两个维度变换的点云分布熵。
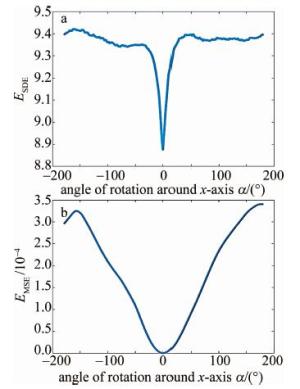
Figure 2. SDE and MSE curve with rotation angle α a—correspondence between SDE and rotation angle b—correspondence between MSE and rotation angle
如图 3所示,SDE与MSE都能很好地反映两组点云的重合程度,当旋转角度为0°时,SDE与MSE均为最小值,适合作为点云配准的评价标准。
在运算速度方面,对不同大小的点云数据,点云分布熵的计算方式都明显优于均值平方差的计算方式,实验数据如表 1所示。
Table 1. Compare between SDE and MSE calculation time
data (point number) time of MSE/s time of SDE/s bunny(35947) 52.4695 0.9349 horse(48485) 86.6042 1.2046 dragon(109411) 262.6325 2.6982 -
针对点云配准问题,其实质就是寻找能使两组点云数据尽可能重合的旋转矩阵[21]。由激光雷达采集获得的激光点云数据因采集视角不同,同一物体的点云数据在空间上存在着刚性变换关系,即两组点云数据中对应点都可通过同一种空间坐标变换方式使之尽可能重合,数学表达式如下式所示:
$ \;\left[ \begin{array}{l} {x_{i, p}}\\ {y_{i, p}}\\ {\rm{ }}{z_{i, p}} \end{array} \right] = {\bm R}\left[ \begin{array}{l} {x_{i, q}}\\ {y_{i, q}}\\ {z_{i, q}} \end{array} \right] + {\bm T}\; $
(4) 式中,p表示目标点云数据,q表示待配准点云数据,R为旋转矩阵,T为平移矩阵。在点云粗配准中,平移矩阵可通过中心化的方式,将两组点云数据的质心移至坐标原点来尽可能的消除平移误差,即:
$ \;\left[ \begin{array}{l} {x_{i, p}}\prime \\ {y_{i, p}}\prime \\ {z_{i, p}}\prime \end{array} \right]{\rm{ = }}{\bm R}\left[ \begin{array}{l} {x_{i, q}}\prime \\ {y_{i, q}}\prime \\ {z_{i, q}}\prime \end{array} \right]\; $
(5) 旋转矩阵R可通过点绕x轴、y轴、z轴旋转的角度α, β, γ确定,其表达方式为:
$ \mathit{\boldsymbol{\;R}}= \left[ {\begin{array}{*{20}{l}} {{\rm{cos}}\alpha {\rm{cos}}\beta {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{cos}}\alpha {\rm{sin}}\beta {\rm{sin}}\gamma {\rm{ - sin}}\alpha {\rm{cos}}\gamma {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{cos}}\alpha {\rm{sin}}\beta {\rm{cos}}\gamma {\rm{ + sin}}\alpha {\rm{sin}}\beta }\\ {{\rm{sin}}\alpha {\rm{cos}}\beta {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{sin}}\alpha {\rm{sin}}\beta {\rm{sin}}\gamma {\rm{ + cos}}\alpha {\rm{cos}}\gamma {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{sin}}\alpha {\rm{sin}}\beta {\rm{cos}}\gamma {\rm{ - cos}}\alpha {\rm{sin}}\gamma }\\ {{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{ - sin}}\beta {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{cos}}\beta {\rm{sin}}\gamma {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{cos}}\beta {\rm{cos}}\gamma } \end{array}} \right] $
(6) 寻找点云配准的最优旋转矩阵即寻找最优的旋转角度α, β, γ。
-
粒子群优化算法是模拟鸟群捕食行为的一种寻优算法[22],它的基本思想是将每一个个体视为n维空间中没有质量和体积的粒子,粒子包含位置与飞行速度两个属性,每一个粒子用一个n维矢量表示,可以视为n维空间中的一个寻优解,在寻优过程中,每个粒子以自身的飞行速度更新自己的位置,通过记录每个位置的适应度来确定个体极值pbest和粒子群体的群体极值gbest,找到全局最优解并由此来调整自己的位置与速度,适应度由目标函数决定。粒子群优化算法通过群体寻优的正反馈机制,根据个体与群体的对目标函数的适应度不断调整个体状态,将个体逐步迁移至较优区域,从而获得目标函数的最优解[23]。
粒子群优化算法中粒子速度v与位置x更新的数学表达如下式所示:
$ \left\{ {_{{x_i}\left( {t + 1} \right) = {x_i}\left( t \right) + {v_i}(t + 1)}^{{v_i}\left( {t + 1} \right) = {v_i}\left( t \right) + {c_1}{r_1}\left( t \right)\left[ {{p_{i, {\rm{best}}}} - {x_i}\left( t \right)} \right] + \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{c_2}{r_2}\left( t \right)\left[ {{g_{{\rm{best}}}} - {x_i}\left( t \right)} \right]}} \right. $
(7) 式中, c1和c2为非负的学习参量; r1, r2为取值范围在(0, 1)之间的随机数,以保证群体的多样性; t表示迭代次数; pi, best为粒子群中第i个粒子所记录的个体适应度极值; gbest为当前整个粒子群中记录的适应度极值,通过设置适合的学习参量并不断迭代逐步获得问题的最优解。
粒子群优化算法虽然在收敛速度上具有优势,但由于缺乏粒子速度的动态调节,容易陷入局部最优,导致在收敛后期的收敛精度低和不易收敛[24]。针对以上问题,可使用天牛须搜索算法为粒子速度调整提供自主寻优的能力。
天牛须搜索算法是2017年提出的一种新型仿生优化算法,在搜索速度和全局搜索方面有一定的优势,可用于粒子群算法粒子速度调节优化[24],其仿生学原理为:自然界里天牛在觅食的过程中,由于不知道食物位置,只能通过气味来寻找食物的大致方向。天牛有左右两个触须,它可通过左右两触须所探测到的气味强度来判断食物在自身位置的左右方位,例如当左须探测到的气味比右触须探测到的气味更强时,天牛向左触须方向移动,移动一段距离后再次使用左右触须探测当前位置食物气味直至找到气味最强即食物的位置。在天牛须搜索算法中,食物的具体位置即为寻优的极值点,食物气味相当于寻优函数本身,通过逐步逼近的方式获得最优解。
天牛须搜索算法的数学表达如下:
(1) 在n维空间中设置质心位置为x,其左触须位置为xl,右触须位置为xr,用d0表示两须之间的距离,根据步长与两须间距离成正比这一特点,可设置步长为:
$ s = c{d_0}\; $
(8) 式中,c是一个设定比例。由于质心的方向是随机的,即右触须指向左触须的向量也是随机的,所以用一个随机n维向量来表示右触须指向左触须的方向,即:
$ \mathit{\boldsymbol{d}} = {\rm{rands}}(n, 1)\; $
(9) (2) 左右触须长度相同,且连线方向的法向量指向质心,则可以根据质心位置x,两须间距d0以及右触须指向左触须的向量d表达左右触须的位置。将d归一化处理后可以得到:
$ {\mkern 1mu} {\kern 1pt} {x_1} - {x_{\rm{r}}} = {d_0}\mathit{\boldsymbol{d}}/\left\| {\mathit{\boldsymbol{ d}}} \right\| $
(10) $ {x_1} = x + {d_0}\mathit{\boldsymbol{d}}/\left( {\left\| \mathit{\boldsymbol{d}} \right\|2} \right) $
(11) $ {x_{\rm{r}}} = x - {d_0}\mathit{\boldsymbol{d}}/\left( {\left\| \mathit{\boldsymbol{d}} \right\|2} \right)\; $
(12) (3) 对于目标函数f,分别求得xl和xr两个位置的值fl和fr, 并比较两个值的大小,为寻求最小值,则当fl < fr时,质心向左须方向移动距离s,当fl>fr时,质心向右须方向移动距离s,可表示为:
$ \left\{ {_{x = x - s({x_{\rm{l}}} - {x_{\rm{r}}}), ({f_{\rm{l}}} > {f_{\rm{r}}})}^{x = x + s({x_{\rm{l}}} - {x_{\rm{r}}}), ({f_{\rm{l}}} < {f_{\rm{r}}})}} \right.{\rm{ }} $
(13) 质心移动后,按照比例改变步长大小:
$ s = \theta s $
(14) 式中,θ为设置的比例系数,一般取值为0.95,循环(2)步、(3)步即可获得最优解。
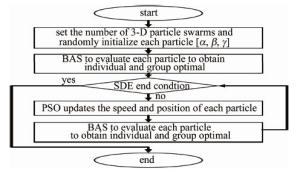
基于天牛须改进的粒子群算法的基本思路是将粒子群中个体最优适应度值的比较过程改为天牛须搜索算法寻优,通过这种方式更新个体与群体的最优适应度值。使用BAS-PSO算法,以点云分布熵作为优化目标求解获得最佳的空间变换关系,设置旋转角度[α, β, γ]为目标解,通过寻找点云分布熵值最小时对应的解[α, β, γ]来获得点云配准时最优的旋转矩阵实现点云粗配准。
该算法的操作步骤如图 4所示。
-
为验证算法可行性及优化效果,作者在Intel Core-i7,8 GB内存的Windows 10操作系统上使用MATLAB R2018a软件对斯坦福大学点云数据库中的bunny, horse, dragon点云进行点云配准实验,以不同视角下的点云数据P, Q为操作对象,使用以点云分布熵为优化目标,基于BAS-PSO算法进行点云粗配准。基于经验对算法中的参量设置如表 2所示。
Table 2. Algorithm parameter setting
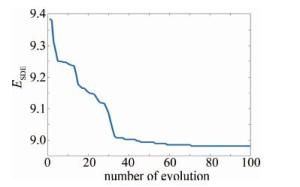
parameter number c1 1.4995 c2 1.4995 θ 0.95 population size 100 number of evolutions 100 step π 为观测BAS-PSO算法中每一代更新后SDE的优化效果,提取出每一代配准后点云的SDE,以bunny模型为例,构建了SDE随进化次数变化的曲线图,如图 5所示。
从图 5中可以看出,随着粒子种群的进化,SDE不断减小并向优化方向进行,在第30次更新种群后,SDE趋于平稳,其值接近于两点云重合时计算获得的DE值,证明BAS-PSO算法是一种有效的优化算法。
针对部分缺失的点云数据以及含有噪声的点云数据,本文中的算法依旧有较好的鲁棒性,配准效果如图 6所示。

Figure 6. Abnormal point cloud data registration effect a—partial cloud missing before registration b—post-registration effect c—point cloud with noise before registration d—post-registration effect
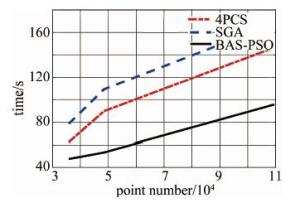
使用BAS-PSO算法配准效果与主成分分析法(principal component analysis, PCA)、四点集法(4-point congruent sets, 4PCS)以及基于遗传算法的粗配准算法进行对比,配准后的模型如图 7所示。对比实验结果如表 3所示。
Table 3. Registration time of different point cloud coarse registration method
4PCS SGA PCA BAS-PSO bunny 62.39s 78.62s 1.02s 47.83s horse 89.74s 109.25s 1.33s 53.55s dragon 146.53s 167.82s 2.11s 95.64s 由仿真结果可知,在粗配准效果上,BAS-PSO算法与4PCS算法以及基于遗传算法的粗配准方法均明显优于PCA算法,在配准速度上,虽然PCA算法速度快,但在考虑配准效果的前提下,BAS-PSO算法优于4PCS算法与基于遗传算法的粗配准方法,如图 8所示。针对不同大小的点云数据,BAS-PSO算法在配准速度上同样具有优势,且针对数据量大的点云数据,配准速度优势越大。
-
提出了一种以点云分布熵为优化目标,基于天牛须改进的粒子群算法用于激光点云数据的粗配准。在优化目标上,点云分布熵计算量明显小于传统ICP算法所使用的均值平方差,且点云分布熵可以准确反映点云配准效果,可作为配准算法中的寻优目标。在寻优算法方面,BAS-PSO算法可以有效弥补天牛须搜索算法个体单一,寻优步长收敛过快,以及粒子群算法易陷入局部最优的问题,实现既精准又快速的点云配准。本文中通过对基于BAS-PSO算法的点云粗配准方法与PCA算法、4PCS算法以及基于遗传算法的点云粗配准方法进行了实验对比,证实了BAS-PSO算法在配准速度上的优势,在点云数据量较大的条件下,BAS-PSO算法也能实现点云的粗配准,为ICP算法提供良好的初始状态。
针对算法中关键参量如搜索步长和学习参量的设定为基于经验的人工手动设定,无法确定是否达到算法最优,寻找一种自动化设置关键参量的方法,保证算法执行效率,提升点云配准效率是下一步需要继续改进的方向。
基于天牛须改进粒子群算法的点云配准方法
Point cloud registration method based on particle swarm optimization algorithm improved by beetle antennae algorithm
-
摘要: 为了提高激光点云配准精度与配准速度,采用了基于天牛须算法改进的粒子群算法,以点云分布熵为寻优目标, 寻找最优空间变换矩阵的点云粗配准,为点云精配准提供良好的初始条件。结果表明,点云分布熵较传统的均值平方差评价方式有更快的计算速度,基于天牛须算法改进的粒子群算法具有全局搜索能力强、计算速度快等特点,与传统点云粗配准方法相比,该方法配准速度提升了近25%;在点云数据量大的条件下,表现出较快的配准速度。这一方法对如何提高激光点云配准速度具有参考意义。Abstract: In order to improve the accuracy and speed of LiDAR point cloud registration, a point cloud coarse entropy that used particle swarm algorithm based on the improved beetle algorithm was adopted. The method useed the point cloud distribution entropy as the optimization target to find the optimal spatial transformation matrix, and provided a good initial condition for the precise registration of the point cloud. Through theoretical analysis and simulation verification, it was proved that the point cloud entropy is an evaluation method which has faster calculation speed than the traditional mean squared difference, and the particle swarm optimization algorithm improved by beetle antennae algorithm has the characteristics of strong global search ability and fast calculation speed. Compared with the traditional point cloud coarse registration method, the registration method has improved the registration speed by nearly 25%. Under the condition of large amount of point cloud data, it still shows a faster registration speed. This method has a reference significance for how to improve the registration speed of laser point cloud.
-
Table 1. Compare between SDE and MSE calculation time
data (point number) time of MSE/s time of SDE/s bunny(35947) 52.4695 0.9349 horse(48485) 86.6042 1.2046 dragon(109411) 262.6325 2.6982 Table 2. Algorithm parameter setting
parameter number c1 1.4995 c2 1.4995 θ 0.95 population size 100 number of evolutions 100 step π Table 3. Registration time of different point cloud coarse registration method
4PCS SGA PCA BAS-PSO bunny 62.39s 78.62s 1.02s 47.83s horse 89.74s 109.25s 1.33s 53.55s dragon 146.53s 167.82s 2.11s 95.64s -
[1] HE Zh B, TIAN Y R. Filtering algorithm for non-ground point from airborne laser scanner data[J]. Journal of Geodesy and Geodyna-mics, 2009, 29(4): 97-101(in Chinese). [2] HUA L, HUANG H Y, CHEN Ch Ch, et al. Three dimensional mo-deling of Hakka earth buildings based on the laser scanned point cloud data[J]. Remote Sensing Technology and Application, 2015, 30(1): 115-122(in Chinese). [3] ZHAO H Y, ZHANG Zh P, et al. The application of 3-D laser point cloud data in the city modeling[J]. Urban Geotechnical Investigation & Surveying, 2009(1): 69-72(in Chinese). [4] CHEN X D, ZHANG J Ch, PANG W S, et al. Key technology and application algorithm of intelligent driving vehicle LiDAR[J]. Opto-Electronic Engineering, 2019, 46(7): 34-46(in Chinese). [5] SHI L, GUO T, PENG Ch, et al. Segmentation of laser point cloud and safety detection of power lines[J]. Laser Technology, 2019, 43(3): 341-346(in Chinese). [6] WU J J, CHEN L, LI L, et al. Power line extraction and reconstruction from airborne LiDAR point cloud[J]. Laser Technology, 2019, 43(4): 64-69(in Chinese). [7] HU X, LI X, ZHANG Y. Fast filtering of LiDAR point cloud in urban areas based on scan line segmentation and GPU acceleration[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 308-312. doi: 10.1109/LGRS.2012.2205130 [8] KEDZIERSKI M, FRYSKOWSKA A. Methods of laser scanning point clouds integration in precise 3-D building modelling[J]. Measurement, 2015, 74: 221-232. doi: 10.1016/j.measurement.2015.07.015 [9] VáZQUEZ-ARELLANO M, REISER D, PARAFOROS D S, et al. 3-D reconstruction of maize plants using a time-of-flight camera[J]. Computers and Electronics in Agriculture, 2018, 145: 235-247. doi: 10.1016/j.compag.2018.01.002 [10] DAI J L, CHEN Zh Y, YE X Z. The application of ICP algorithm in point cloud alignment[J]. Journal of Image and Graphics, 2007, 12(3): 517-521(in Chinese). [11] LI T Sh, WANG Y M, HU Ch M. Research on automatic point cloud registration based on laser reflection intensity[J]. Bulletion of Surveying and Mapping, 2014(s2):143-145. doi: 10.1145/2661229.2661239 [12] BESL P J, McKAY N D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1992, 14(2): 239-256. doi: 10.1117/12.57955 [13] BOUAZIZ S, TAGLIASACCHI A, PAULY M. Sparse iterative closest point[J]. Computer Graphics Forum, 2013, 32(5):12-14. [14] RUSINKIEWICZ S, LEVOY M. Efficient variants of the ICP algorithm[J]. Proceedings of the SPIE, 2001, 1497:149701. [15] WU D L, HUANG H L, DING Y Ch, et al. Surfaces matching algorithm based on genetic algorithm and least square criterion[J]. Acta Aeronautica ET Astronautica Sinica, 2002, 23(3): 285-288(in Chinese). [16] DUAN D Q, LI J F, SHEN P P, et al. Registration of scattered cloud point data based on PSO[J]. Journal of Guangxi Normal University(Natural Science Edition), 2008, 26(3): 226-229(in Chinese). [17] SHE X X, XU B. Improved particle swarm opetimization algorithm based on genetic thought[J]. Journal of Yangtze University(Natural Science Edition), 2016, 13(22): 4-8(in Chinese). [18] XIANG Y J, SHUAI L. Beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1):37-42. [19] CHEN J, CAI Y, ZHANG J Sh. Point cloud registration based on entropy criterion genetic algorithm[J]. Application Research of Computers, 2019, 36(1): 322-326(in Chinese). [20] LI H X. Lidar point cloud feature analysis and data segmentation[D].Xi'an: Xidian University, 2014: 57-64(in Chinese). [21] TAO H Q, DA F P. Automatic registration algorithm for the point clouds based on the normal vector[J]. Chinese Journal of Lasers, 2013, 40(8):809001(in Chinese). doi: 10.3788/CJL201340.0809001 [22] SHI Y. A modified particle swarm optimizer[J].Proceedings of the SPIE, 1998, 7803:699146. [23] UGOLOTTI R, CAGNONI S. Multi-objective parameter tuning for PSO-based point cloud localization[M].Berliln, Germary: Springer International Publishing, 2014:75-85. [24] CHEN T T, YIN H, JINAG H L, et al. Particle swarm optimization algorithm based on beetle antennae search for solving portfolio pro-blem[J]. Computer Systems & Applications, 2019, 28(2): 171-176(in Chinese). -


 网站地图
网站地图

 下载:
下载: