-
近几年, 我国雾天发生的频率越来越高,雾天是常见的低能见度天气现象,做好雾天能见度的测量,对于民航具有重要意义[1-2]。激光透射仪是通过测量激光在大气中传输的透过率,然后依据比尔定律计算消光系数,从而得到能见度[3]。但是比尔定律只考虑光的单次散射,随着雾天气下能见度的降低,大气中雾滴粒子的密度增加,粒子的散射效应显著提高,产生严重的多次散射,使得接收的激光能量增大,这时如果直接使用比尔定律,就会过高地估计雾天大气的能见度。因此,为了准确做好雾天能见度的测量,必须考虑激光传输过程中雾滴粒子的多次散射特性。
多次散射现象是激光在大气中传输存在的重要问题。近年来,国内外相关学者对不同低能见度条件下的多次散射传输衰减特性进行了一些研究。YANG等人[4]研究了电磁波在沙尘天气下的多次散射和衰减特性,能见度越低多次散射影响越明显。ANTHONY[5]在研究光学厚度较大的介质中的多次散射雷达方程时,强调了多次散射的重要性。WANG等人[6]采用蒙特卡洛法模拟了激光在煤烟、沙尘中的传输过程,指出蒙特卡洛法可以很好地模拟激光的多次散射传输过程。尽管人们对不同条件下的多次散射进行了一些研究,但是这些研究的重点各不相同,实际应用比较困难,对于常见的雾天气,其传输衰减的研究也比较多。ZHAO等人[7]研究了不同雾模型下大气含水量和能见度对红外辐射光传输衰减特性的影响。LI等人[8]研究了地面雾和山顶雾在可见光和红外波段的消光特性。KE等人[9]分析了雾的前向散射对激光传输的影响。LIN等人[10]模拟分析了辐射雾条件下多次散射对非视距大气散射光通信信道传输特性的影响。但是迄今为止的研究成果都没有考虑雾滴粒子的多次散射对激光大气透射仪能见度测量的影响。
因此,本文中将针对常见的平流雾和辐射雾分布模型,应用蒙特卡洛法[11-14]模拟激光在雾中的传输过程,并结合激光大气透射仪的系统参量,计算不同雾分布模型下的多次散射特性,通过比较考虑多次散射的透过率和比尔定律计算得到的透过率,分析不同雾分布模型下多次散射对激光透过率测量的影响,进一步计算了不同接收机直径下多次散射引起的能见度测量误差,对实际雾天气下激光大气透射仪能见度的准确测量提供重要依据。
-
结合大气中能见度的定义,由Koschmieder定理推导出能见度的计算公式:
$ V = - \frac{{{\rm{ln}}\varepsilon }}{\sigma } $
(1) 式中,V是能见度,σ是消光系数,ε是人眼观测阈值,其值通常取0.05,故(1)式可表示为:
$ V = \frac{{2.996}}{\sigma } $
(2) 因此准确计算消光系数,即可获得准确的大气能见度。
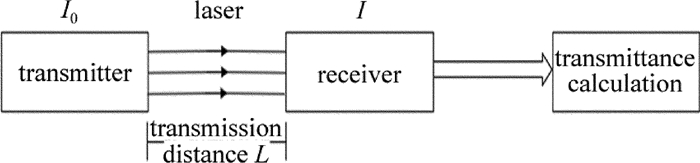
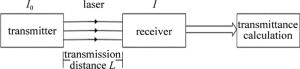
激光大气透射仪工作原理[15]如图 1所示。假设发射机发射的光强为I0,激光通过传输距离为L的气体后被接收机接收,接收机接收到的光强为I。因此计算透过率为:
$ T = \frac{I}{{{I_0}}} $
(3) 不考虑多次散射的情况下,依据比尔定律即可得到在一定传输距离L后的透过率为:
$ I = {I_0}{\rm{exp}}( - \sigma L) $
(4) 根据以上各式,即可得到激光大气透射仪测量能见度的计算公式:
$ V = - \frac{{2.996L}}{{{\rm{ln}}T}} $
(5) 但是在雾天气条件下,雾滴粒子密度很大时,多次散射光强不能被忽略,使得激光大气透射仪接收探测到的光强增大,透过率T增大,这时如果直接使用上式计算雾天气下的能见度,就会产生较大的误差,因此, 必须考虑雾天粒子的多次散射对激光大气透射仪能见度测量的影响。
-
雾天是比较常见的低能见度天气,它是由大气中许多细小的水珠凝结形成的胶体系统[16]。常见的雾模型分为平流雾和辐射雾,不同模型的粒径分布与含水量之间的关系见下[17]。
平流雾模型:
$ \begin{array}{*{20}{c}} {n(r) = 3.73 \times {{10}^5}{w^{ - 0.804}}{r^2} \times }\\ {{\rm{exp}}( - 0.2392{w^{ - 0.301}}r)({{\rm{m}}^{{\rm{ - 3}}}} \cdot {\rm{ \mathit{ μ} }}{{\rm{m}}^{{\rm{ - 1}}}})} \end{array} $
(6) 辐射雾模型:
$ \begin{array}{*{20}{c}} {n(r) = 5.4 \times {{10}^7}{w^{ - 1.104}}{r^2} \times }\\ {{\rm{exp}}( - 0.5477{w^{ - 0.351}}r)({{\rm{m}}^{{\rm{ - 3}}}} \cdot {\rm{ \mathit{ μ} }}{{\rm{m}}^{{\rm{ - 1}}}})} \end{array} $
(7) 式中, n(r)为粒径分布函数; r为雾滴粒子的半径;w为含水量。
图 2为含水量w=0.6g/m3时平流雾和辐射雾的粒径分布。由图可以看出,在相同含水量的情况下辐射雾的粒径分布明显大于平流雾。
-
雾滴粒子是大气中最接近球型的粒子,其主要成分是水,所以使用水的折射率进行计算。能见度定义中所选取的光源是波长为550nm的光波,因此本文中主要选择波长为550nm的激光,应用Mie散射理论计算雾滴粒子的散射特性。
根据Mie散射理论可知,单个粒子散射光的光强在全空间积分与垂直于入射光方向上的截面截获的光强之比,称为散射截面;对应于散射光和吸收光光强的全空间积分称为消光截面;吸收截面等于消光截面与散射截面之差。无纲量的单个球形粒子的散射、消光和吸收效率因子由相应的截面除以垂直于入射光方向上的几何截面得到。消光效率因子Qext、散射效率因子Qsca和吸收效率因子Qabs随雾滴粒子半径的变化如图 3所示。当雾滴粒子的半径大于2μm时,其吸收效率因子几乎为零,消光与散射效率因子随着半径的增大趋向于定值2。所以本文中不考虑雾滴粒子对光的吸收作用。非对称因子g随雾粒子半径的变化如图 4所示。随着粒子半径的增大,非对称因子的值在0.88上下振荡。由于雾滴粒子的半径在2μm~30μm之间[18],所以本文中不考虑雾滴粒子对光吸收作用。
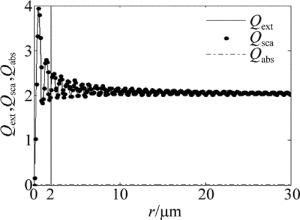
Figure 3. The extinction, scattering and absorption efficiency with respect to the radius of fog particle
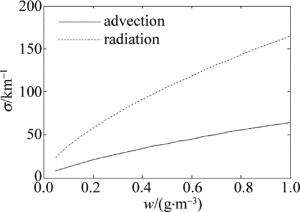
当大气中粒子数密度较低时,可以不考虑多次散射,则此时具有一定粒径分布的气溶胶粒子的总消光系数为:
$ \sigma = \int_0^\infty \pi {r^2}{Q_{{\rm{ext}}}}(r)n(r){\rm{d}}r $
(8) 式中, n(r)为粒径分布函数,Qext(r)为单个粒子的消光效率因子。图 5是550nm的激光在不同雾模型下的消光系数随含水量变化的仿真图。由图可以看出,随着大气中含水量的增多,不同模型下的消光系数都逐渐变大。在同一含水量条件下,辐射雾的消光系数大于平流雾,这是由于在相同含水量的情况下, 辐射雾的粒子数密度较大,所以辐射雾消光系数偏大。
-
激光在粒子浓度较大的介质中传输时,接收机接收到的光强除直接透射光强和经过一次散射的光强外,有一部分被一次散射的光强通过其它粒子的再一次或者多次散射到达接收机,这种现象就称之为多次散射。因此,这就使得透射仪接收到的光强不仅包含一次散射光强还包含多次散射光强。蒙特卡洛法是模拟激光传输的常用方法,只要模拟的光子数足够多,就能准确地模拟激光的传输过程。因此,本文中将应用蒙特卡洛法模拟光子在不同雾天模型下的传输。
-
根据光的粒子性,运用蒙特卡洛法模拟激光在雾中的传输过程,本文中不考虑粒子的吸收,即单次散射反照率为1。蒙特卡洛法模拟激光传输步骤简述如下。
-
假设光子从O点出发,初始偏转角θ0在发散角2θ1内均匀发射,初始方位角φ0在[0, 2π]间均匀分布,则光子的初始传输方向D0为:
$ {\mathit{\boldsymbol{D}}_0} = \left[ {\begin{array}{*{20}{c}} {{u_{{x_0}}}}\\ {{u_{{y_0}}}}\\ {{u_{{z_0}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{sin}}{\theta _0}{\rm{cos}}{\varphi _0}}\\ {{\rm{sin}}{\theta _0}{\rm{sin}}{\varphi _0}}\\ {{\rm{cos}}{\theta _0}} \end{array}} \right] $
(9) 式中, ux0,uy0,uz0分别为传输方向D0的x, y, z轴坐标。光子的随机运动步长lm可根据比尔定律抽样表示为:
$ {l_m} = - \frac{1}{\sigma }{\rm{ln}}r $
(10) 因此光子第1次散射的位置P1点坐标为:
$ {P_1}({x_1},{y_1},{z_1}) = O(0,0,0) + {l_m}{\mathit{\boldsymbol{D}}_0} $
(11) -
本文中选取了Henyey- Greenstein(HG)散射相函数[19]确定光子每次碰撞之后的散射角,则光子在每次与雾滴粒子碰撞后,其散射角θs可以表示为:
$ {\theta _{\rm{s}}} = {\rm{arcos }}\left\{ {\frac{1}{{2g}}\left[ {1 + {g^2} - \frac{{{{(1 - {g^2})}^2}}}{{{{(1 + g - 2gr)}^2}}}} \right]} \right\} $
(12) 方位角φs在[0, 2π]内均匀分布,则φs为:
$ {\varphi _{\rm{s}}} = 2\pi r $
(13) 则光子第m次碰撞后的迁移方向为:
$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{D}}_m} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{sin}}{\theta _{\rm{s}}}}}{{\sqrt {1 - {u_{{z_m}}}^\prime } }}({u_{{x_m}}}^\prime {u_{{z_m}}}^\prime {\rm{cos}}{\varphi _{\rm{s}}} - {u_{{y_m}}}^\prime {\rm{sin}}{\varphi _{\rm{s}}}) + {u_{{x_m}}}^\prime {\rm{cos}}{\theta _{\rm{s}}}}\\ {\frac{{{\rm{sin}}{\theta _{\rm{s}}}}}{{\sqrt {1 - {u_{{z_m}}}^{\prime 2}} }}({u_{{x_m}}}^\prime {u_{{z_m}}}^\prime {\rm{cos}}{\varphi _{\rm{s}}} + {u_{{x_m}}}^\prime {\rm{sin}}{\varphi _{\rm{s}}}) + {u_{{y_m}}}^\prime {\rm{cos}}{\theta _{\rm{s}}}}\\ { - {\rm{sin}}{\theta _{\rm{s}}}{\rm{cos}}{\varphi _{\rm{s}}}\sqrt {1 - {u_{{z_m}}}^{\prime 2}} + {u_{{x_m}}}^\prime {\rm{cos}}{\theta _{\rm{s}}}} \end{array}} \right] \end{array} $
(14) 式中,uxm′,uym′,uzm′分别指上一个状态m次碰撞后x, y, z轴坐标,则第m次碰撞后的光子位置坐为:
$ {P_{m + 1}}({x_{m + 1}},{y_{m + 1}},{z_{m + 1}}) = {P_m}({x_m},{y_m},{z_m}) + {l_m}{\mathit{\boldsymbol{D}}_m} $
(15) -
光子的接收判断有如下两种情况:光子恰好到达接收机圆面或者光子的迁移轨迹穿越接收机探测圆面时,在实际探测中都看作光子被接收,本文中假设全视场角接收光子。
-
可得到考虑多次散射的透过率:
$ T = \frac{{{n_0} + {n_1} + {n_2} + \cdots }}{N} $
(16) 式中, N为发射的总光子数,n0为不经过粒子散射直接被接收机接收到的光子数,n1为经过粒子1次散射得到的光子数,n2为经过粒子2次散射得到的光子数。此时,依据能见度的计算公式(5)式即可得到考虑多次散射的大气能见度。
-
基于以上多次散射计算模型,对激光在雾天进行模拟仿真,模拟过程中的参量设置如下:总模拟光子数为106个;激光束发散角为0.06mrad;接收机直径1m;传输距离为30m;探测激光波长为550nm;雾滴粒子的单次散射反照率取值为1;非对称因子为0.88。
-
图 6是依据第4.1节中的算法,模拟仿真了激光在不同雾模型下各次散射光子占总接收光子比例随含水量变化的曲线。4条曲线分别代表了1次~4次散射光子占总接收光子的比值。由图可以看出,随着雾天空气中含水量的增大,各次散射光子占总接收光子的比例均增大。在含水量为1g/cm3时,平流雾模型下1次、2次、3次和4次散射所占比例分别为18.48%, 3.25%, 0.68%和0.16%。辐射雾模型下1次、2次、3次和4次散射所占比例分别为27.73%, 13.04%, 7.0%和4.42%。在相同含水量的情况下,辐射雾模型的各次散射光子占总接收光子比例比平流雾模型大,这是因为在相同含水量的情况下,辐射雾的粒子数密度都远远高于平流雾,所以发生散射的光子数多。
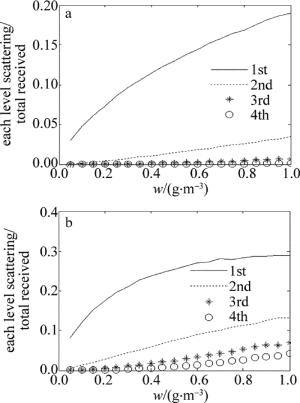
Figure 6. Photons ratio of each scattering order relative to the total received photons with respect to the water content for different fog models
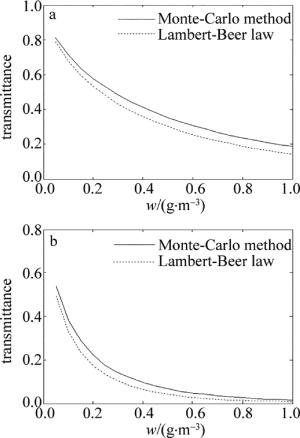
图 7分别是激光在平流雾和辐射雾模型下,依据蒙特卡洛法(Monte-Carlo method)和朗伯-比尔定律(Lambert-Beer law)得到的考虑多次散射的透过率计算结果,并与基于朗伯-比尔定律的透过率进行比较。由图中可以看出,在两种分布模型下透过率都随含水量的增多下降,在同一含水量的条件下,辐射雾的透过率小于平流雾的透过率。随着含水量的增多,两者计算得到的透过率差别也越大。为了更准确地得到多次散射引起的透过率误差,表 1中选取了3个含水量不同点计算了多次散射引起的透过率相对误差。其定义为蒙特卡洛法与朗伯-比尔定律得到的透过率之差与比尔定律的透过率结果的比值。从表中可以直观地看出,含水量越大,透过率相对误差越大。在含水量w=1g/cm3时,辐射雾的透过率相对误差高达116.76%,这说明随着大气中含水量的增大,多次散射对激光大气透射仪透过率测量的影响越大。
Table 1. Transmittances relative error caused by multiple scatterings for different fog models
water content/(g·cm-3) transmittances relative error /% advection fog radiation fog 0.2 8.61 26.47 0.6 20.02 68.70 1 30.48 116.76 -
依据不同雾模型下的透过率,基于激光大气透射仪能见度计算公式(5)式,表 2中计算了不同接收机直径下,含水量为1g/cm3时的能见度相对误差。其定义为依据蒙特卡洛法与朗伯-比尔定律的透过率计算得到的能见度之差与依据朗伯-比尔定律的能见度计算结果的比值。由表 2可以看出,同一条件下辐射雾的能见度相对误差大于平流雾,不同雾模型下激光大气透射仪的接收机直径越大,多次散射引起的能见度相对误差越大。
Table 2. Visibility relative error caused by multiple scatterings for different fog models
receiver diameter/cm visibility relative errors /% advection fog radiation fog 100 15.79 19.30 60 9.08 11.03 20 2.81 3.59 -
本文中基于不同雾模型下的粒径分布与大气含水量的关系,应用米散射理论计算了单个雾滴粒子的单次散射特性,并计算了不同雾模型下具有一定尺度分布气溶胶粒子的单次散射衰减,随着雾天空气中含水量的增大,衰减系数也增大。这主要是由于大气中雾滴粒子增多引起的,因此随着雾滴粒子的增多,多次散射明显,所以要对雾天粒子的传输特性做更深入的研究。
应用蒙特卡洛法模拟了激光在不同雾模型中的传输过程,计算了各次散射光子占总接收光子的比例,计算了考虑多次散射时的透过率,并与比尔定律的透过率计算结果进行比较,分析了雾天多次散射对激光大气透射仪能见度测量的影响,结果表明:(1)随着含水量的增多,各次散射占总接收光强的比例逐渐增大;(2)含水量较大时,能见度越低,透过率相对误差也越大,相同条件下辐射雾的透过率相对误差大于平流雾;(3)同一条件下透射仪的接收直径越大,能见度测量误差就越大。
本文中的研究结果对实际雾天气下激光大气透射仪能见度的测量具有重要的指导意义,选取适当的接收机直径可以有效抑制多次散射对能见度测量的影响。本文中的研究仅考虑了雾天的水滴粒子,而实际大气中气溶胶种类复杂,还需对复杂天气下的多次散射特性做更深入的研究。
雾天多次散射对激光透射仪能见度测量的影响
Multiple-scattering effects on the visibility measurement of laser transmissometers in fog
-
摘要: 为了分析雾天多次散射引起的激光透射仪能见度测量误差,结合激光大气透射仪的系统参量,基于平流雾和辐射雾分布模型,采用蒙特卡洛法对激光在雾中的传输特性进行了理论分析和数值模拟,获得了雾天透过率数据,并计算得到了多次散射引起的能见度误差。结果表明,在雾天气下随着空气中含水量的增多,多次散射越明显,透过率测量误差越大,辐射雾的透过率相对误差高达116.76%;同等条件下,当接收机直径为100cm时,辐射雾多次散射引起的能见度测量误差为19.30%;同时选取较小的接收机直径可以减小多次散射引起的能见度测量误差。因此, 在雾天应用激光透射仪进行能见度测量时,需考虑多次散射的影响。此研究结果对实际雾天气下激光大气透射仪能见度的测量具有重要的指导意义。Abstract: The visibility errors induced by the multiple-scattering effects are further discussed considering the system parameters of the laser transmissometers, which have been regarded as promising visibility meters used in airports around the world. Based on the size distributions of the advection fog and radiation fog, the transmission of photons is simulated numerically using the Monte-Carlo method. It is noted that the multiple-scattering effects would become more serious for larger water content of the fog, which may cause significant visibility errors as the outputs of the transmissometers. The relative error of transmittance of radiation fog is even possible to achieve 116.76%, and the error of visibility caused by multiple scattering of radiation fog is 19.30% when the diameter of receiver is 100cm. The simulation results further reveal that reducing the receiver aperture may sufficiently suppress the multiple-scattering effects. It is necessary to consider the multiple-scattering effects on the visibility measurement especially for the low-visibility atmosphere, e.g., in dense fog and haze, which gives us important hints on the visibility measurement of laser transmissometers in dense fog and haze.
-
Key words:
- scattering /
- visibility measurement /
- Monte-Carlo method /
- advection fog /
- radiation fog
-
Table 1. Transmittances relative error caused by multiple scatterings for different fog models
water content/(g·cm-3) transmittances relative error /% advection fog radiation fog 0.2 8.61 26.47 0.6 20.02 68.70 1 30.48 116.76 Table 2. Visibility relative error caused by multiple scatterings for different fog models
receiver diameter/cm visibility relative errors /% advection fog radiation fog 100 15.79 19.30 60 9.08 11.03 20 2.81 3.59 -
[1] ZHUANG Z B, HUANG W, FU Ch, et al. Portable visibility detector based on backward scattering lidar[J]. Laser Technology, 2015, 36(1): 119-123(in Chinese). [2] XING X L, LIU W J, JIANG L H, et al. Slant-range visibility retrieve considering multiple-scattering effects[J]. Journal of Optoelectronics·Laser, 2014, 25(9): 1742-1748(in Chinese). [3] LIU Ch Y. Study of visibility measurement error based on laser-transmissomerer[D]. Tianjin: Civil Aviation University of China, 2016: 7-32(in Chinese). [4] YANG R K, LI Q Q, YAO R H, et al. Multiple scattering and attenuation for electromagnetic wave propagation in sand and dust atmosphere[J]. Acta Physica Sinica, 2016, 65(9): 094205 (in Chinese). [5] DAVIS A B. Some new lidar equations for laser pulses scattered back from optically thick media such as clouds, dense aerosol plumes, sea ice, snow, and turbid coastal waters[J]. Proceedings of the SPIE, 2013, 8872: 88720E. doi: 10.1117/12.2025341 [6] WANG H X, ZHU Y Zh, TIAN T, et al. Characteristics of laser transmission in different types of aerosols[J]. Acta Physica Sinica, 2013, 62(2): 024214 (in Chinese). [7] ZHAO Zh W, WU Zh S, SHEN G D, et al. Attenuation due to fog for 10.6μm wavelength[J]. Journal of Infrared and Millimeter Waves, 2002, 21(2):95-98(in Chinese). [8] LI X B, GONG Ch W, LI Ch, et al. Size distribution and attenation for infrared radiation of fog particles[J]. Laser & Infrared, 2009, 39(7): 742-745(in Chinese). [9] KE X Zh, MA D D, LIU J N, et al. Study attenuation of laser transmission in fog[J]. The Journal of Light Scattering, 2009, 21(2): 104-109(in Chinese). [10] LIN Y, XU Zh Y, WANG J Y, et al. Analysis of effect of multiple scattering on non-line-of-sight scattering communication in fog weather[J]. Acta Photonica Sinica, 2014, 43(1): 1-4(in Chinese). [11] GRABNER M, KVICERA V. Multiple scattering in rain and fog on free-space optical links[J]. Journal of Lightwave Technology, 2014, 32(3): 513-520. doi: 10.1109/JLT.2013.2294356 [12] LI J, MA Y, ZHOU Q Q, et al. Monte Carlo study on pulse response of underwater optical channel[J]. Optical Engineering, 2012, 51(6): 0660011. [13] BURAS R, MAYER B. Efficient unbiased variance reduction techniques for Monte Carlo simulations of radiative transfer in cloudy atmospheres: The solution[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2011, 112(3): 434-447. doi: 10.1016/j.jqsrt.2010.10.005 [14] NORTH P R J, ROSETTE J A B, SUÁREZ J C, et al. A Monte Carlo radiative transfer model of satellite waveform LiDAR[J]. International Journal of Remote Sensing, 2010, 31 (5): 1343-1358. doi: 10.1080/01431160903380664 [15] XIONG X L, LIU Ch Y, JIANG L H, et al. Effects of multiple scattering on visibility measurement error of laser-transmissometer [J]. Journal of Optoelectronics·Laser, 2015, 26(10): 199-206(in Chinese). [16] LI D, CHEN H. Study on attenuation characteristic of laser propagation in rain and fog[J]. Electronic Design Engineering, 2011, 19(9): 1-5(in Chinese). [17] GONG J M, LI Ch, JIANG X B, et al. Analysis of non-line-of-sight ultraviolet light multiple scattering path losses in fog environment[J]. Study on Optical Communications, 2016, 193(1): 67-70(in Chinese). [18] SONG B, WANG H X, LIU M, et al. Raindrop size distribution model for applicability analysis of rain attenuation[J]. Laser and Infrared, 2012, 42(3): 310-313(in Chinese). [19] GURDEV L, DREISCHUH T, BLIZNAKOVA I, et al. Scattering of a laser beam in turbid media with forward-peaked Henyey-Greenstein indicatrices[J]. Physica Scripta, 2012, 149: 014074. doi: 10.1088/0031-8949/2012/T149/014074 -


 网站地图
网站地图

 下载:
下载: