-
光电伺服平台是一种集光、机、电为一体的复杂高精度定向跟踪系统,被广泛应用于海陆空等领域中,主要用来实现对运动目标的实时精密跟踪和测量[1-3]。在各种应用场景中,光电伺服平台在实际运行过程中又会受到摩擦力矩、电机力矩波动、风载扰动以及其它各种非线性因素的影响,造成系统的跟踪性能降低。采用传统的比例-积分-微分(proportional-integral-derivative, PID)控制技术,在建模时一般做近似处理,忽略系统中存在的一些非线性因素,建立一个线性的数学模型,由此设计的控制器,光电伺服平台的闭环性能很难获得较大的提升[4]。而滑模控制(sliding mode control, SMC)对系统参量变化和各类扰动不敏感,具有鲁棒性好、响应速度快及物理实现简单等优点[5],可以对上述不确定因素进行有效抑制。参考文献[6]中采用积分滑模变结构控制消除了高精度光电伺服稳定平台由非线性摩擦所引起的低速“爬行”现象。参考文献[7]中提出了一种基于有限时间扰动观测器的连续非奇异终端滑模控制方法,使得系统输出即使在多源扰动存在情况下,也可在有限时间内快速收敛到平衡点,从而提高光电跟踪系统的抗干扰能力与稳态控制精度。然而当光电伺服平台进行大幅值阶跃信号跟踪时,系统的初始误差较大,控制器会输出一个较大的控制量,同时由于伺服电机受电流、转速等因素的影响以及出于安全考虑而人为加入的限幅器,都会导致电机的输出被限制在一定的允许范围内,这种情况下系统就会产生输入饱和问题[8]。通过一些方法可以避免产生饱和现象,如适当降低控制器增益,将控制器输出限制在线性区域内,但是该方法会导致系统性能降低[9]。因此,研究一种能够有效解决饱和问题的控制方法具有重大的工程应用价值。
针对输入饱和问题,国内外学者已经有了很多研究[10-14]。参考文献[15]中提出了一种指令滤波器法来解决无人驾驶飞行器的饱和问题,但是该方法的设计过程过于复杂,不易于工程实现。参考文献[16]中提出了抗饱和控制来解决具有执行器饱和现象的航天器大角度姿态控制问题,然而该方法无法从理论上证明其稳定性。因此,设计一种形式简单、易于实现且能够保证系统稳定的控制方法来解决饱和问题是十分必要的。本文中采用滑模控制算法设计外环控制器,提出一种新的过渡过程算法(transition process, TP)来解决饱和问题。过渡过程算法通过将一个快速变化的阶跃信号变为一个缓慢上升的输入信号,减小系统初始跟踪误差,从而使控制器输出一个较小的控制量,避免了驱动饱和现象,提高了系统的稳定性。经过大量理论仿真和实验验证,该算法在光电伺服平台上取得了较好的控制效果。
-
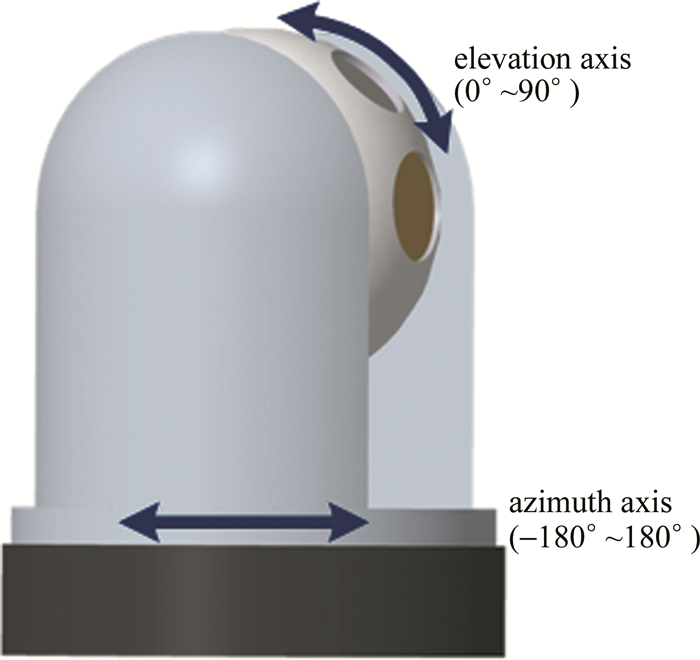
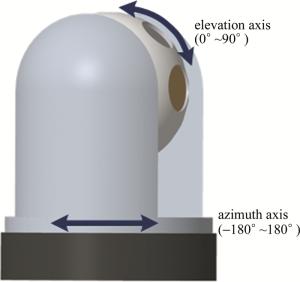
光电伺服平台是由俯仰轴和方位轴共同组成的,结构如图 1所示。由于俯仰轴和方位轴在空间上是相互独立,控制方法一致,因此本文中选择方位轴作为研究对象。
其位置开环模型可以描述为如下2阶被控对象模型:
$ \ddot \theta (t) + {a_1}\dot \theta (t) + {a_0}\theta (t) = bu(t) + d(t) $
(1) 式中,θ(t)是实验平台的视轴相对于载体基座的相对角位移;u(t)为控制量;d(t)为系统所受到的总外部扰动;a0,a1和b是简化后的系数,可以通过实验测得。
令x1=θ(t),x2=$\dot \theta $(t),将上述微分方程(1)式转化为状态空间方程:
$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{Dd}}}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}}} \end{array}} \right. $
(2) 式中,是系统的最大角速度。
假设1:外界扰动d(t)是可观测的和有界的,且满足$\tilde D$≥|d(t)|max。其中,$\tilde D$是外界总扰动的上界值。
-
光电伺服平台在实际运行过程中会受到模型参量变化和众多外部扰动的影响,造成系统的闭环性能降低。而滑模控制对系统参量变化和各类外部扰动不灵敏,具有鲁棒性好、响应速度快及物理实现简单等优点,被广泛应用于这一类控制系统中。
滑模控制本质上是一类特殊的非线性控制,与其它控制的不同之处在于系统“结构”不固定,可以在动态过程中,根据系统当前状态,有目的地不断变化,迫使系统沿预定“滑动模态”的状态轨迹运动[5]。
对于(2)式,按如下步骤设计滑模控制器。
首先,定义系统跟踪误差为:e=r-x1,$\dot e = \dot r - {x_2}$, $\ddot e = \ddot r - {\dot x_2}$。其中,r,e,$\dot e$和$\ddot e$分别是目标位置信号、位置跟踪误差、速度跟踪误差和加速度跟踪误差。
选取线性滑模面为:
$ s = ce + \dot e $
(3) 式中,系数c>0。
对(3)式进行求导可得:
$ \begin{array}{*{20}{c}} {\dot s = c\dot e + \ddot e = }\\ {c(\dot r - {x_2}) + (\ddot r - {{\dot x}_2}) = }\\ {c\dot r - c{x_2} + \ddot r + {a_0}{x_1} + {a_1}{x_2} - bu - d} \end{array} $
(4) 20世纪,中国学者GAO院士提出了趋近律的概念,其目的是通过设计不同的趋近律,改善系统趋近过程的动态品质[17]。采用指数趋近律:
$ \dot s = - ks - \varepsilon {\rm{sgn}}s $
(5) 式中,k和ε都是正数。可以通过调整参量k和ε的大小来改变趋近速度和抖振程度。
结合(4)式和(5)式可得如下控制器:
$ \begin{array}{l} u = \frac{1}{b}(\ddot r + c\dot r - c{x_2} + {a_0}{x_1} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_1}{x_2} + ks + q{\rm{sgn}}s) \end{array} $
(6) 式中,q>ε+$\tilde D$。
对滑动模态的稳定性进行分析,考虑如下李雅普诺夫函数:
$ {V = \frac{1}{2}{s^2}} $
(7) 对V求导可得:
$ {\dot V = s\dot s} $
(8) 函数V是正定的,根据李雅普诺夫稳定性条件只要其导数负定就能保证系统渐进稳定,即$\dot V$ < 0。
结合(4)式、(6)式和(8)式可得:
$ \begin{array}{*{20}{c}} {\dot V = s(c\dot r - c{x_2} + \ddot r + {a_0}{x_1} + {a_1}{x_2} - bu - d) = }\\ {s( - ks - q{\rm{sgn}}s - d) = }\\ { - k{s^2} - sd - q|s| \le }\\ { - sd - q|s|} \end{array} $
(9) 因为q>$\tilde D$≥|d|,所以:
$ \dot V = 0 $
(10) 因此,当系统中存在外部扰动d(t)时,控制器表达式(6)式中的鲁棒项qsgns就可以使系统不受外界扰动的影响,使系统保持稳定。
-
尽管滑模控制对外界干扰具有强鲁棒性的优点,但是在光电伺服平台上使用滑模控制器进行大幅值阶跃信号跟踪时,系统依然会产生执行器饱和现象。
从(3)式可知,系统误差越大,滑模面s就越大。结合(6)式可知,此时控制量u也就越大。当光电伺服平台进行大幅值阶跃信号跟踪时,由于系统的初始误差较大,滑模控制器会输出一个较大的控制量,同时由于执行机构的物理限制以及出于安全考虑而人为加入的限幅器,电机的驱动量被限制在一定范围内,此时系统就会产生执行器饱和现象。
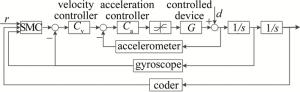
为了充分说明饱和问题,可以将滑模控制器应用到光电伺服平台上,搭建如图 2所示的仿真框图。内环可以提高系统的稳定性,加速度环和速度环采用传统的PID控制器,位置环采用本文中提出的滑模控制器。由于本实验平台的执行机构允许输出的驱动量范围是-1024~1024,因此仿真中设计的饱和器的输出上限是1024,输出下限是-1024。仿真结果如图 3所示。
从图 3a中可以看出,当系统采用滑模控制器时,系统输出可以快速无超调地跟踪上输入信号。但是从图 3b中可以看出,系统的驱动输出发生了饱和现象,和上面的理论分析保持一致。执行器饱和是一种非线性特性,会导致系统的稳定性变差,因此需要在实际工程中避免掉。
-
为了解决上述问题,本文中提出使用合适的过渡过程方法,来减小系统的初始跟踪误差,从而消除驱动饱和现象。基于时间最优控制理论,本文中提出了一种新的过渡过程算法。通过使跳变的输入信号r变为一个缓慢上升的信号,从而让系统在跟踪输入信号的整个过程中都保持一个较小的误差,避免了输入饱和现象。
考虑如下系统状态方程:
$ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}}\\ {{{\dot x}_2} = u} \end{array}} \right. $
(11) 式中,x1=rTP, x2=$\dot r$TP。
系统初始条件和终端条件分析为:
$ \left\{ {\begin{array}{*{20}{l}} {{x_1}(0) = 0,{x_1}({t_{\rm{f}}}) = {r_{\rm{a}}}}\\ {{x_2}(0) = 0,{x_2}({t_{\rm{f}}}) = 0} \end{array}} \right. $
(12) 式中,ra是阶跃信号的幅值, 初始时间为0, tf是终止时间。
从实际应用角度出发,系统控制输出总有一个极限值。因此,控制约束为:
$ |u| \le {a_{{\rm{max}}}},(0 \le t \le {t_{\rm{f}}}) $
(13) 式中,amax是最大角加速度。
求取如下性能指标取极小的最优控制:
$ J = \int_0^{{t_{\rm{f}}}} {\rm{d}} t = {t_{\rm{f}}} $
(14) 通过构造哈密顿函数可求得最优解为:
$ u(t) = \left\{ {\begin{array}{*{20}{l}} {{a_{{\rm{max}}}},(0 \le t < {t_1})}\\ { - {a_{{\rm{max}}}},({t_1} < t \le {t_{\rm{f}}})} \end{array}} \right. $
(15) 结合初始条件和终端条件,对(15)式进行二次积分可得:
$ {r_{{\rm{TP}}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}{a_{{\rm{max}}}}{t^2},(0 \le t \le {t_1})}\\ { - \frac{1}{2}{a_{{\rm{max}}}}{{(t - {t_{\rm{f}}})}^2} + {r_{\rm{a}}},({t_1} < t < {t_{\rm{f}}})}\\ {{r_{\rm{a}}},({t_{\rm{f}}} \le t)} \end{array}} \right. $
(16) 式中,${t_1} = \sqrt {\frac{{{r_{\rm{a}}}}}{{{a_{{\rm{max}}}}}}} $,${t_{\rm{f}}} = \sqrt {\frac{{4{r_{\rm{a}}}}}{{{a_{{\rm{max}}}}}}} $。
由(16)式可知,过渡信号rTP分为3个时间段。第1个时间段是加速阶段[0, t1],从0开始以amax为加速度沿抛物线上升; 第2个时间段是减速阶段[t1, tf],以-amax为加速度沿抛物线上升到设定值ra; 第3个时间段是在tf时刻以后维持在设定值上。
-
为了验证本文中设计的控制策略的有效性和优越性,在MATLAB软件平台下,建立系统仿真模型,如图 4所示。其中,$G = 6.9025 \times \frac{{{s^2} + 19.3s + 3725000}}{{{s^2} + 320s + 4000000}} \times \frac{{{s^2} + 18s + 1000000}}{{{s^2} + 195.2s + 1488000}}, {C_{\rm{v}}} = 280 \times \frac{{0.16s + 1}}{{0.0016{s^2} + s}}, \\{C_{\rm{a}}} = 1.2 \times \frac{{0.06s + 1}}{{0.0016s + 1}} \times \frac{{0.0006561{s^2} + 0.078s + 1000}}{{1.6{s^2} + s}}$,扰动信号d=sint,限幅器的范围为-1024~1024,传感器都为单位反馈。
用SMC和基于过渡过程的滑模控制算法(sliding-mode control based on transiton process, TPSMC)分别跟踪60°阶跃信号来验证方法的有效性和先进性,仿真结果如图 5所示。实线是当系统采用SMC控制策略时每个变量的曲线,虚线是当系统采用TPSMC控制策略时每个变量的曲线。图 5a中是位置输出曲线,其中r代表原始阶跃信号,SMC代表采用SMC控制策略时的位置输出,rTP代表由过渡过程设计的输入信号,TPSMC代表采用TPSMC控制策略时的位置输出; 图 5b中是驱动输出曲线。
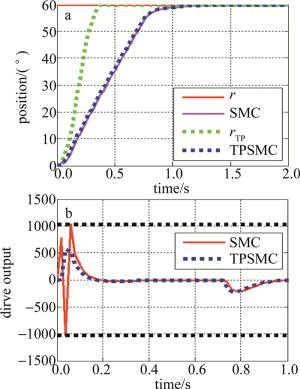
Figure 5. Simulation comparison of position output and drive output when two control strategies track 60° step signals respectively
从图 5a中可以看出,当系统采用滑模控制器时,系统的位置输出是没有超调的,且响应速度足够快。从图 5b中可以看出,当系统采用SMC的控制策略时,驱动饱和现象发生在控制过程的开始阶段,且驱动输出存在震荡现象。而系统采用TPSMC控制策略后,系统的驱动输出不再有饱和现象,且消除了震荡现象,保证了系统的稳定性。由此可知,采用本文中提出的控制方法,在不影响系统的响应速度的前提下,可以更好地消除驱动饱和现象,提高系统的稳定性。
-
实验平台如图 6所示。主要由控制器、驱动装置、传感器等几部分组成。电机采用永磁同步直流电机,允许输出的驱动量范围是-1024~1024。位置传感器采用光电编码器,速度传感器采用微机电系统陀螺,加速度传感器采用加速度计,控制器采用MSM800+PC104集成模块,加速度传感器和速度传感器的采样频率是1kHz,位置传感器的采样频率是50Hz,实验测得平台的最大加速度amax=1664.9°/s2。永磁同步电机的参量如表 1所示。
Table 1. Motor parameters
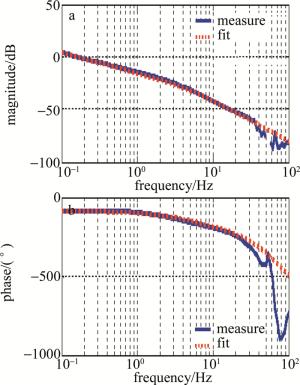
parameter value rated voltage 60V rated current 4.6A rated torque 30N·m moment coefficient 3.5N·m/A stator inductance 16.3mH stator resistance 11.5Ω 采用扫频法对(2)式中的参量a1,a2和b进行辨识,得到其位置开环频率响应曲线如图 7所示。实线代表测量曲线,虚线代表拟合曲线。拟合出的参量为:。
为了能够充分说明当系统分别采用SMC和TPSMC跟踪大范围角度时的对比情况,实验中分别跟踪了30°,60°和90°的输入信号,以跟踪误差最小为指标优化得到一组滑模参量q=1.5,k=20,c=14,实验结果如图 8~图 10所示。定量实验结果如表 2所示。图中的各变量定义与仿真结果图中的变量定义保持一致。
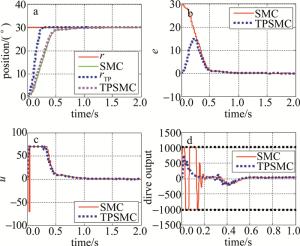
Figure 8. Experimental comparison of position output and drive output when two control strategies track 30° step signals respectively
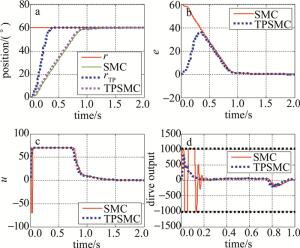
Figure 9. Experimental comparison of position output and drive output when two control strategies track 60° step signals respectively
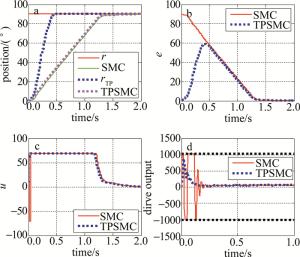
Figure 10. Experimental comparison of position output and drive output when two control strategies track 90° step signals respectively
Table 2. Experimental result
step signal control strategy saturation problem error fluctuation/% 30° SMC yes 100 TPSMC no 46.7 60° SMC yes 100 TPSMC no 61.7 90° SMC yes 100 TPSMC no 66.7 定义误差波动量为:
$ \delta = \frac{{|{e_{{\rm{max}}}}| + |{e_{{\rm{min}}}}|}}{r} \times 100\% $
(17) 式中,emax是系统跟踪过程中产生的最大误差值,emin是系统跟踪过程中产生的最小误差值,r是目标阶跃信号,误差波动量用来衡量系统在跟踪目标的过程中误差的变化情况。从图 8a~图 10a中的实验结果对比可知,SMC和TPSMC都可以快速无超调的跟踪上目标信号,这与上述仿真结果相验证;从图 8、图 9、图 10的b, c, d小图和表 2中的实验结果对比可知,当采用SMC控制策略时,系统的初始误差较大,滑模控制器此时输出了一个较大的控制量,导致电机驱动输出值超出了-1024~1024,产生饱和现象,而当采用TPSMC控制策略时,由于过度过程算法将一个快速变化的阶跃信号变为了一个缓慢上升的输入信号,使系统在跟踪输入信号的整个过程中都保持一个较小的误差,从而消除了驱动饱和现象,提高了系统的稳定性,这与上述理论分析和仿真结果相一致。实验结果表明,基于过渡过程的滑模控制无超调,稳态误差小,驱动输出平缓,适合应用于光电伺服平台的目标跟踪,具有重要研究与应用价值。
-
光电伺服平台在实际运行过程中会受到各种非线性扰动的影响,造成系统跟踪精度降低。为了减小外界扰动对系统跟踪性能的影响,本文中利用滑模控制算法鲁棒性好、响应快速和实现简单的优点,设计滑模控制器进行系统目标的定点跟踪。然而当光电伺服平台进行大幅值阶跃信号跟踪时,执行机构会产生驱动饱和现象。因此,引入过渡过程算法,通过将一个快速变化的阶跃信号变为一个缓慢上升的输入信号,减小了系统初始跟踪误差,从而避免了驱动饱和现象,极大地提高了系统的稳定性。仿真和实验数据表明, 该控制策略适合应用于光电伺服平台的目标跟踪,具有重要的研究与应用价值。
具有输入饱和的光电伺服平台的滑模控制
Sliding mode control of the photoelectric servo platform with input saturation
-
摘要: 为了解决光电伺服平台中的输入饱和问题,采用了基于过渡过程的滑模控制算法。过渡过程算法是基于时间最优理论设计的,将跳变的输入信号变为一个缓慢上升的信号,使系统的初始跟踪误差减小,从而避免了输入饱和现象,提高了系统的稳定性。结果表明,该方法可以有效消除输入饱和现象,适用于光电伺服平台的目标跟踪,具有重要研究与应用价值。Abstract: In order to solve the input saturation problem in the optoelectronic servo platform, a sliding mode control algorithm based on the transition process is adopted. The transition process algorithm is designed based on the time-optimal theory, which makes the hopping input signal become a slowly rising signal, so that the initial tracking error of the system is decrease, thus avoiding the input saturation phenomenon and greatly improving the system stability. After theoretical analysis and experimental verification, the results show that the proposed method can effectively eliminate the input saturation phenomenon and is suitable for target tracking of the optoelectronic servo platform and has important research and application value.
-
Key words:
- laser technique /
- input saturations /
- sliding mode control /
- transition process
-
Table 1. Motor parameters
parameter value rated voltage 60V rated current 4.6A rated torque 30N·m moment coefficient 3.5N·m/A stator inductance 16.3mH stator resistance 11.5Ω Table 2. Experimental result
step signal control strategy saturation problem error fluctuation/% 30° SMC yes 100 TPSMC no 46.7 60° SMC yes 100 TPSMC no 61.7 90° SMC yes 100 TPSMC no 66.7 -
[1] DIERKS J S, ROSS S E, BRODSKY A, et al. Relay mirror experiment overview - a gbl pointing and tracking demonstration[J/OL].[2019-10-25]. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/1482/1/Relay-Mirror-Experiment-overview--a-GBL-pointing-and-tracking/10.1117/12.45692.short?SSO=1. [2] SCHNEEBERGER T J, BARKER K W. High-altitude balloon experiment: A tested for acquisition, tracking, and pointing technologies[J/OL].[2019-10-25]. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/1950/0000/High-altitude-balloon-experiment--a-testbed-for-acquisition-tracking/10.1117/12.156595.short. [3] LI G H, OU L, XIE Ch L, et al. Optical axis stabilization technology based on FSM on a vehicle platform[J]. Laser Technology, 2018, 42(4): 470-475(in Chinese). [4] LIU J. Research on low-speed servo system of large telescope based on permanent magnet synchronous motor[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics Chinese Academy of Sciences, 2018: 6(in Chinese). [5] LIU J K. Sliding mode control design and MATLAB simulation[M].3th ed. Beijing: Tsinghua University Press, 2005: 1-3(in Chinese). [6] ZHOU Y, WANG L, ZHOU T. Integral sliding mode variable structure control of high precision EO servo-stabilized platform[J]. Opto-Electronic Engineering, 2010, 37(7): 12-15(in Chinese). [7] MAO J L, LI Q, ZHU H R. Continuous nonsingular terminal sliding mode control of optical-electronic tracking system subject to multiple disturbances[J]. Control Theory & Applications, 2017, 34(4): 413-423(in Chinese). [8] ZHOU L M. Study of theory and application for control systems subject to actuator saturation[D]. Harbin: Harbin Engineering University, 2009: 4(in Chinese). [9] SOURLAS D, CHOI J, MANOUSIOUTHAKIS V. Best achievable control system performance: The saturation paradox[C]//Proceedings of 1994 33rd IEEE Conference on Decision and Control. New York, USA: IEEE, 1994: 5044094. [10] CHEN M, ZHOU Y L, GUO W W. Robust tracking control for uncertain MIMO nonlinear system with input saturationusing RWNNDO[J]. Neurocomputing, 2014, 144(20): 436-447. [11] GRONARDF F, SEPULCHRE R, BASTIN G. Improving the performance of low-gain designs for bounded control of linear systems[J]. Automatica, 2002, 38(10): 1777-1782. doi: 10.1016/S0005-1098(02)00086-9 [12] CHAOUIF F, GIRI F, SAAD M. Asymptotic stabilization of linear plants in the presence of input and output saturations[J]. Automatica, 2001, 37(1): 37-42. doi: 10.1016/S0005-1098(00)00120-5 [13] GRUNE L, PANNEK L. Nonlinear model predictive control[M]. London, UK: Springer-Verlag, 2011: 89-96. [14] FARRELL A, POLYCARPOU M, SHARMA M, et al. Command filtered backsteopping[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395. doi: 10.1109/TAC.2009.2015562 [15] FARRELL J, SHARMA M, POLYCARPOU M. Backstepping-based flight control with adaptive function approximation[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(6): 1089-1102. [16] BANG H, TANK M J, CHIO H D. Large angle attitude control of spacecraft with actuator saturation[J]. Control Engineering Practice, 2003, 11(9): 989-997. doi: 10.1016/S0967-0661(02)00216-2 [17] GAO W B. Theoretical basis of variable structure control[M]. Beijing: China Science and Technology Press, 1990: 28-30(in Chin-ese). -


 网站地图
网站地图

 下载:
下载: