-
随着硅集成电路技术的成熟,非制冷红外焦平面阵列的制造成本大幅降低,这使得红外成像系统在各类武器装备中得以普及,并成为了军事对抗中图像采集的重要途径[1-2]。与此同时,为了占领信息化对抗的制高点,针对红外成像系统的激光压制干扰技术也悄然兴起,对其干扰机理、方法和效果的研究成为了人们关注的焦点。非制冷微测辐射热计是红外成像系统的核心部件,其在一定能量激光的辐照下会出现饱和致盲,甚至损毁的现象。对这一方向的研究,一方面为激光干扰武器的研发提供理论指导,另一方面为红外侦察系统开发抗干扰功能提供参照,因而具有重要意义。
本文中结合非制冷微测辐射热计的构造和工作原理,分析了像元的温度响应机制,建立了激光辐照非制冷微测辐射热计的模型。以激光辐照非晶硅红外探测器为例,对不同能量激光的损伤效果展开了研究,结合材料的实际参量,采用有限元分析的方法进行了仿真,得出了有意义的结论。
-
非制冷微测辐射热计是红外探测器的核心部件,它的工作主要依托光敏材料制成的微桥结构进行。当红外波段的光辐照至光敏材料时,除透射和反射的能量之外,被吸收的能量转化为材料的内能。微观上主要表现为三部分[3]:晶格振动产生并传播声子;电子吸收光子引起跃迁到导带;发生激子吸收,逐步转化能量。三者共同作用带来了热激发,获得能量的电子挣脱了原子核的库伦作用,这增加了自由载流子的浓度,从而提高了光敏材料的电导率。实时采集不同像元的电阻性能变化,经处理即可得到具备一定分辨率的红外图像。
-
非制冷微测辐射热计主要由三部分组成[4]:光学系统、红外焦平面阵列和电气系统,其中电气系统包括驱动电路板和图象处理板。目标辐射的远红外光经光学透镜成像于焦平面的像元阵列,像元升温,电阻发生变化,驱动电路板提供偏置电压并逐行采集像元信号进行前处理,图像处理板将传输来的像素信号经一系列后处理最终得到红外图像。
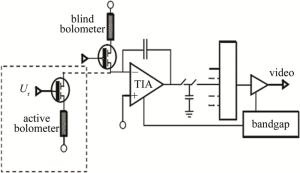
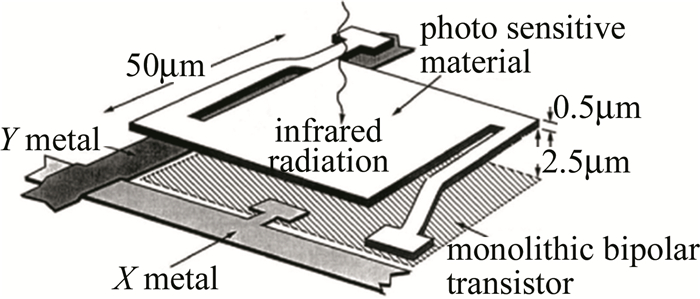
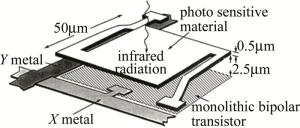
为了得到较好的工作性能,非制冷微测辐射热计的像元多为Ⅰ型微桥结构[5](见图 1)。图 2为典型读出电路的架构。其中盲元可有效抑制背景电流;通常利用脉冲式直流电压偏置,并采集像元产生的电流信号,将其整合到放大器(trans impedance amplifier, TIA)中,在下一个信号流入前,该信号被保持、复用并放大。探测器工作时,阵列的信号被逐一采集,由主时钟按固定的频率产生控制信号,使得以上工作可以同步进行[6]。对于每秒50帧或60帧的成像机制,像元相应地每秒受到偏置作用50次或60次,时间一般不大于120μs[7]。
-
在像素读出的过程中,与像元连接的金属氧化物半导体(metal oxide semiconductor,MOS)场效应晶体管起到了采集像元信号的关键作用。由于偏置电阻的存在,使得在恒定大小的总偏置电压的作用下,施加在像元上的分压随着其电阻的变化而变化。该电压信号经MOS管线性放大,转化为电流信号,然后被TIA采集和使用。MOS管的栅源电压被定义为像元两端电压Ur,设其开启电压Uth,漏源电压Ud, s,跨导系数β,随着Ur的逐渐减小,MOS管的漏源电流可描述为:
$ {I_{{\rm{d,s}}}} = \left\{ {\begin{array}{*{20}{l}} {\beta \left[ {({U_{\rm{r}}} - {U_{{\rm{th}}}}){U_{{\rm{d,s}}}} - \frac{{{U_{{\rm{d,s}}}}^2}}{2}} \right],}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le {U_{{\rm{d,s}}}} \le {U_{\rm{r}}} - {U_{{\rm{th}}}}, {\rm{linear}} )}\\ {\frac{{\beta {{({U_{\rm{r}}} - {U_{{\rm{th}}}})}^2}}}{2},(0 \le {U_{\rm{r}}} - {U_{{\rm{th}}}} \le {U_{{\rm{d,s}}}},{\rm{ saturated }})}\\ {0,({U_{\rm{r}}} - {U_{{\rm{th}}}} \le 0,{\rm{ closing }})} \end{array}} \right. $
(1) 该电流信号就是处理成像素值的原始数据,MOS管的工作状态对应该像元的工作状态。由于制造工艺的限制,各像元的光电性能有所差异,因而需要进行非均匀校正,使得所有像元对目标区域红外辐射的响应性能一致。一般情况下,基于非制冷微测辐射热计的红外成像系统会带有光学增益的功能,它能够有效地呈现视野中的目标形态。这一功能较为复杂,本文中不作考虑。为了使各像元拥有相等的参照温度,像元下方为恒定温度的衬底,它通过连接的热电制冷器(thermo electric cooler, TEC)来实现。
-
在激光的辐照下,非制冷微测辐射热计温度不断升高,直到发生损伤,它可以被分软损伤和硬损伤,二者的区别在于损伤是否能够恢复。当辐照激光能量密度达到一定程度时,微测辐射热计的像元饱和,像素值达到最大,撤去激光后像元会自动恢复,发生了软损伤;随着激光能量密度的继续增大,被辐照像元的微桥结构内沉积了过多的热量无法及时导出,光敏材料受到热熔融破坏,发生不可恢复的硬损伤。
-
若功率为P0的远红外激光受到角频率ω的正弦调制后,均匀辐照至非制冷微测辐射热计的像元表面,有热平衡方程:
$ C\frac{{{\rm{d}}(\Delta \mathit{\boldsymbol{T}})}}{{{\rm{d}}t}} + G \cdot \Delta \mathit{\boldsymbol{T}} = {P_{\rm{b}}} + \eta {P_0}{\rm{exp}}({\rm{j}}\omega t) $
(2) 式中, C为热容,G为热导,T为温度,Pb表示偏置电压导致的焦耳热,η为光敏面对光的吸收率,${\rm{j}} = \sqrt { - 1} $。由于非制冷微测辐射热计的工作温度区间相对较小,因而可近似地将C和G视作定值。零偏置下Pb=0,解这个1阶微分方程,得:
$ \Delta {\mathit{\boldsymbol{T}}_{\rm{z}}} = \eta {P_0} \cdot \frac{{{\rm{exp}}({\rm{j}}\omega t)}}{{G + {\rm{j}}\omega C}} $
(3) 利用(3)式,可计算出零偏置下微测辐射热计光敏面温度增量$\left| {\Delta {\mathit{\boldsymbol{T}}_{\rm{z}}}} \right| = \eta {P_0}/\sqrt {{G^2} + {\omega ^2}{C^2}} $。
-
若像元电阻为R,由电阻温度系数的定义[8],$\alpha = \frac{1}{R}\frac{{{\rm{d}}R}}{{{\rm{d}}T}}$,其中T为像元的温度大小。考虑到探测器的工作温度范围内α变化微小,因而可视作常数。因此:
$ R = {R_0}{\rm{exp}}[\alpha (T - {T_0})] = R(T) $
(4) 式中,R0为温度初始温度T0下像元的电阻。在恒压U作用下,由电路的基本原理知Pb=U2R/(Pb+R)2=Pb(T)。Rb为偏置电阻,考虑到电流偏置时间极短,在T=T0处取Pb的1阶泰勒展开式近似:
$ \begin{array}{*{20}{c}} {{P_{\rm{b}}}(T) \approx {{\left. {\frac{{{\rm{d}}{P_{\rm{b}}}}}{{{\rm{d}}T}}} \right|}_{T = {T_0}}} \cdot (T - {T_0}) + {P_{\rm{b}}}({T_0}) = }\\ {\frac{{{U^2}\alpha {R_0}}}{{{{({R_{\rm{b}}} + {R_0})}^3}}}[{R_{\rm{b}}} + (1 - 2\alpha ){R_0}] \times }\\ {(T - {T_0}) + \frac{{{U^2}{R_0}}}{{{{({R_{\rm{b}}} + {R_0})}^2}}}} \end{array} $
(5) 显然, T-T0=|ΔT|,将(5)式代入(2)式并整理,得:
$ \begin{array}{*{20}{c}} {C\frac{{{\rm{d}}(\Delta \mathit{\boldsymbol{T}})}}{{{\rm{d}}t}} + [G - \frac{{{U^2}\alpha {R_0}}}{{{{({R_b} + {R_0})}^3}}}({R_{\rm{b}}} + (1 - 2\alpha ){R_0})] \times }\\ {\Delta \mathit{\boldsymbol{T}} = \frac{{{U^2}{R_0}}}{{{{({R_{\rm{b}}} + {R_0})}^2}}} + \eta {P_0}{\rm{exp}}({\rm{j}}\omega t)} \end{array} $
(6) 注意到(6)式与(2)式形式相同,用类似的方法解得,单次偏置的时间内像元温度增量:
$ \begin{array}{*{20}{l}} {|\Delta {\mathit{\boldsymbol{T}}_{\rm{b}}}| = \left| {\frac{{{U^2}{R_0}}}{{{G^\prime }{{({R_{\rm{b}}} + {R_0})}^2}}}\left[ {1 - {\rm{exp}}\left( { - \frac{{{G^\prime }}}{C}t} \right)} \right] + } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta {P_0} \cdot \frac{{{\rm{exp}}({\rm{j}}\omega t)}}{{{G^\prime } + {\rm{j}}\omega C}}} \right|} \end{array} $
(7) 式中,$G' = G - \frac{{{U^2}\alpha {R_0}}}{{{{\left( {{R_{\rm{b}}} + {R_0}} \right)}^3}}}\left[ {{R_{\rm{b}}} + \left( {1 - 2\alpha } \right){R_0}} \right]$。
利用(7)式,将非制冷微测辐射热计像元的相应参量代入,消去虚数单位j,即可近似计算出一次偏置时间内光敏面的温度增量。
-
非制冷微测辐射热计受到软损伤的必要条件是像素值达到饱和,对应像元温度达到其饱和温度,设为Ts。在偏置电路中,像元两端电压Ur=RU/(R+Rb)。又由(1)式可知,像元饱和时Ur=Uth+Ud, s,由此得出像元饱和时的温度为:
$ \begin{array}{*{20}{l}} {{T_{\rm{s}}} = {T_0} + \frac{1}{\alpha } \cdot {\rm{ln}}\left( {\frac{{{R_{\rm{b}}}}}{{{R_0}}} \cdot \frac{{{U_{\rm{r}}}}}{{U - {U_{\rm{r}}}}}} \right) = {T_0} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{\alpha } \cdot {\rm{ln}}\left( {\frac{{{R_{\rm{b}}}}}{{{R_0}}} \cdot \frac{{{U_{{\rm{th}}}} + {U_{{\rm{d,s}}}}}}{{U - {U_{{\rm{th}}}} - {U_{{\rm{d,s}}}}}}} \right)} \end{array} $
(8) -
非制冷微测辐射热计受到硬损伤时,像元的光敏材料温度达到了熔点,设为Th,发生相变。这一过程中,材料的热物理性质不再固定,(2)式中的参量C和G都随着温度的变化而发生变化,(3)式和(7)不再适用,仅能根据温度Th达到光敏材料熔点来判断。
-
基于实际设备的参量及工作条件,利用Solid works软件建立3维模型,并设定仿真条件,利用ANSYS Workbench展开有限元分析,一方面对前文温度响应的推导进行验证,另一方面探究一定损伤条件下激光损伤阈值及其与调制频率的关系。值得注意的是,该方法已经通过大量数值验证是正确的[9-12]。
-
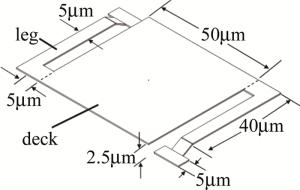
基于法国ULIS公司设计的UL01011型320×240 α-Si非制冷微测辐射热计的相关参量,建立了3-D模型(见图 3)。为了便于计算,将像元的尺寸做了适当简化。
该设备的相关参量如表 1所示[6]。在阵列进行非均匀矫正时,偏置电压U会根据各像元的热电性能被设定为不同的值。像元采用图 1的结构,由金属真空封装。
Table 1. Typical parameters of UL01011 320×240 α-Si uncooled microbolometer
parameter value wavelength 8μm~14μm absorption η 80% temperature dynamic range 0K~90K thermal conductance G 1×10-7W/K heat capacity C 4×10-9J/K temperature coefficient of resistance α -0.025K-1 resistance R0 20kΩ bias resistor Rb 20kΩ bias boltage U 0.5V~3.3V -
激光损伤非制冷微测辐射热计这一问题的关键在于元件的温度,因此采用ANSYS Workbench的瞬态热分析模块展开研究。由于元件置于真空环境中,因而没有空气对流的影响。
-
为了使模型具有表 1的热物理性质,做如下处理。
将模型沿虚线处区分开(见图 3),使模型的微桥面与两桥腿分别被定义成两种材料。微桥面主要功能为吸收光能,温度升高,并通过偏置电路提供像素值。硅材料的质量密度ρ=2.33g/cm3,在300K的温度下热导率κ=0.151W/(mm·K)。将光敏材料的比定压热容定义成:
$ {c_p} = \frac{C}{{\rho {V_{\rm{d}}}}} = 1.37{\rm{J}}/({\rm{g}} \cdot {\rm{K}}) $
(9) 式中,Vd是微桥光敏材料的体积。在热分析中,桥腿的作用主要为传导热量,将它的热导率定义为:
$ {\kappa _{{\rm{leg}}}} = \frac{G}{{\sum\limits_{i = 1}^2 {\frac{{{S_i}}}{{{L_i}}}} }} \approx 5.7 \times {10^{ - 4}}{\rm{W}}/({\rm{mm}} \cdot {\rm{K}}) $
(10) 式中,S和L分别是微桥腿的截面积和长度。其余参量均采用表 1中的数值。
-
根据微测辐射热计的实际工作机理,像元主要受到3项载荷的作用。
(1) 偏置电压引起的焦耳热。用于采集像元信号的电流会产生热量,显然,它可以等效为材料自身产生的体热源。取U=2V,由于320×240阵列中的像元被逐行偏置,因此对于输出50Hz的PAL制视频的红外探测器而言,在每个周期(1s/50=20ms)内,像元被偏置电压作用的时间是64μs[10]。所以,这个体热源可表示为:
$ \begin{array}{*{20}{l}} {{P_1} = \left\{ {\begin{array}{*{20}{l}} {{P_{\rm{e}}},(n \cdot 20{\rm{ms}} \le t \le n \cdot 20{\rm{ms}} + 64{\rm{ \mathsf{ μ} s}})}\\ {0,(n \cdot 20{\rm{ms}} + 65{\rm{ \mathsf{ μ} s}} \le t \le (n + 1) \cdot 20{\rm{ms}})} \end{array},} \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (n = 1,2,3, \cdots )} \end{array} $
(11) 其中,
$ \begin{array}{*{20}{c}} {{P_{\rm{e}}} = \frac{{U_{\rm{r}}^2}}{R} \cdot \frac{1}{{{V_{\rm{d}}}}} = }\\ {160\{ {\rm{exp}}[0.025(T - 300)] + }\\ {{\rm{exp}}[ - 0.025(T - 300)] + 2{\} ^{ - 1}}{\rm{W}}/{\rm{m}}{{\rm{m}}^3}} \end{array} $
(12) 式中,Vd是光敏材料的体积。
(2) 激光辐照,使其温度升高。像元的光敏材料厚度为0.5μm,远小于硅对于远红外激光的吸收厚度(0.7mm)[3],可以认为是体加热。同时注意到,微桥结构与衬底形成的谐振腔[13]大大增加了像元对红外辐射的吸收率。为简化研究,忽略光敏材料对激光吸收率的纵向差异,认为激光在材料内部发生了均匀吸收,将激光辐照等效为材料自身产生的体热源。该热源可表示为:
$ {P_2} = \frac{{\eta {P_0}}}{{{V_{\rm{d}}}}}{\rm{exp}}({\rm{j}}\omega t) $
(13) (3) 在微桥两脚底,固定于衬底的两个接触面发生散热。在像元正常工作的情况下,被TEC制冷的衬底保持恒温来提供参照温度,这一载荷为接触面上固定大小的温度;而当辐照激光能量过大,微桥温度过高时,像元进入饱和状态,TEC的制冷能力不足以散去多余的热量。在这样的情况下,这一载荷可简化为固定大小的散热功率。
-
主要围绕两方面内容进行仿真。
(1) 微测辐射热计的温度响应。为了证明(3)式,假设P1=0,微桥模型两脚底恒温300K,按照表 2的取值进行仿真,总时长1s。
Table 2. Parameters of simulation 1, 2
No. P0/W P2/(W·mm-3) ω/(rad·s-1) 1 1.6×10-6 5 0 2 7.8×10-5 10 100 为了证明(7)式,根据(11)式录入热载荷P1,按照表 3的取值进行仿真,总时长64μs。
Table 3. Parameters of simulation 3, 4
No. P0/W P2/(W·mm-3) ω/(rad·s-1) 3 0 0 0 4 3.4×10-6 2.5 0 (2) 微测辐射热计的激光损伤。区分软损伤和硬损伤两种情况,软损伤是指像素值达到最大,像元饱和,撤去激光后迅速恢复;硬损伤是指像元温度过高,像点破坏,造成了不可恢复的损伤。
软损伤。根据表 1中的温度动态范围,取饱和时温度增量|ΔT|=Ts-T0=80K,在仿真4的基础上,不断增大P0,直到模型求解得到的稳态温度达到Ts=T0+80K=380K,此时的P0是ω=0时的软损伤阈值;然后改变ω,通过同样的方法得到P0。处理数据即可得到,对探测器造成软损伤的激光参量。
硬损伤。在材料温度大幅升高的过程中,其热物理性质会发生非线性变化,微测辐射热计的比热容和热导不可视为定值,热平衡方程(2)式不再适用。对这一问题,将在后续工作中另作研究。
-
在ANSYS中,利用公式编辑器生成APDL命令,并插入Workbench的瞬态热分析模块中,实现了复杂热源函数的定义。在设定的条件下,将理论计算结果与仿真结果进行对比,证明了公式;对该模型的激光损伤条件进行了仿真分析。
-
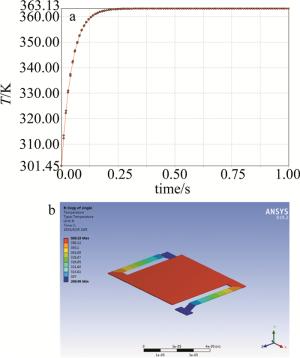
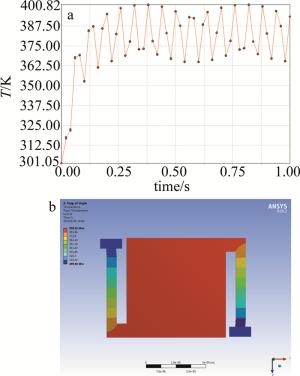
根据(3)式,仿真1中设定温度应为T=T0+|ΔTz|=362.50K,软件仿真得出,模型在稳态下的最高温度为363.13K,如图 4所示。
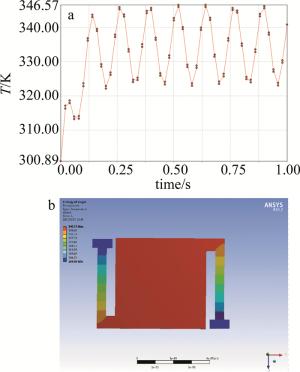
仿真2中设定温度应为T=T0+|ΔTz|=330.31695K,经ANSYS仿真,稳态下模型在333K附近震荡,如图 5所示。
仿真1和仿真2的结果产生的误差主要是由于式的计算中取了近似值,(3)式得证。
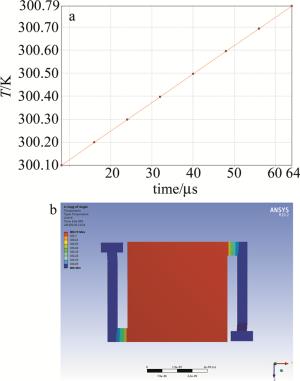
根据(7)式,仿真3的最终温度应为T=T0+|ΔTb|=300.80K;软件仿真结果中,稳态下的最高温度为300.79K,如图 6所示。
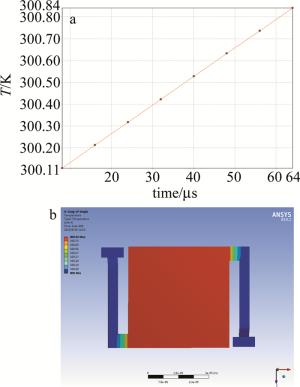
仿真4的最终温度应为T=T0+|ΔTb|=300.85K,经ANSYS仿真,模型最终温度是300.84K,如图 7所示。(7)式得证。
-
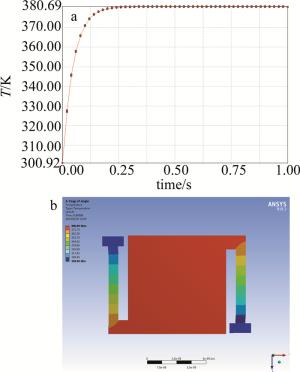
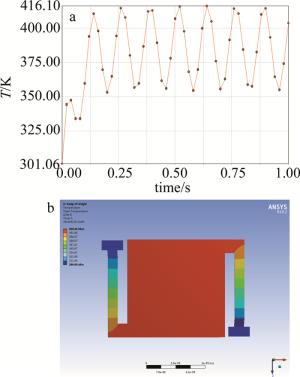
为了研究激光诱导非制冷微测辐射热计的软损伤,为使模型最高温度在380K上下振荡,录入热载荷函数P1和P2,进行了数次仿真实验,得到了3组有效数据,如表 4所示。其中Te表示稳态(即像元饱和)下模型的温度浮动均值。对应的温度变化曲线和温度分布如图 8~图 10所示。
Table 4. Effective simulation parameters of laser soft damage caused by laser
No. Te/K P2/(W·mm-3) ω/(rad·s-1) P0/W 5 380.69 6.3 0 1.0×10-5 6 386.32 15 50 2.5×10-5 7 382.45 27 100 4.2×10-5 将表 4中的P0和ω代入(3)式,得到零偏置下像元温度增量为:
$ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\left| {{\kern 1pt} {\kern 1pt} \Delta {\mathit{\boldsymbol{T}}_{{\rm{s,5}}}}{\kern 1pt} {\kern 1pt} } \right| = 78.75{\rm{K}}}\\ {|\Delta {\mathit{\boldsymbol{T}}_{{\rm{s,6}}}}| = 83.85{\rm{K}}} \end{array}}\\ {|\Delta {\mathit{\boldsymbol{T}}_{{\rm{s,7}}}}| = 81.86{\rm{K}}} \end{array}} \right. $
(14) 对比表 4中的ΔTe可知,电压偏置的作用对像元升温的贡献很小。在参考文献[14]和参考文献[15]的研究中,偏置电路对热成像的影响很小,这也从侧面证明了这一结论。因此在对非制冷红外探测器进行激光干扰造成软损伤时,在调制角频率的作用下激光损伤阈值可通过(3)式计算。由以上温度计算结果可以得到,对应偏差率依次为2.4%,2.9%,0.7%。初步得出,(3)式计算出的损伤阈值对应温度偏差不大于3%。
在激光压制干扰红外成像系统的损伤阈值计算问题中,根据(3)式及其结果可知,在较低角频率(ω≪G/C)的正弦调制下,ω的改变对激光损伤阈值的影响不大;而当调制角频率较大(ω≫G/C)时,ω与对应条件下的激光损伤阈值近似成倒数关系。
-
介绍了非制冷微测辐射热计的构造和成像机理,根据热平衡方程,区分零偏置和工作状态两种情况推导了像元温度增量的计算公式;基于UL01011型320×240 α-Si非制冷微测辐射热计建立了模型,根据实际工作情况展开了有限元分析,证明了像元温度响应的计算公式。通过设定条件,仿真了激光干扰造成软损伤的过程,经对比分析得出结论:在不考虑光学增益的前提下,激光干扰非制冷微测辐射热计的软损伤阈值可利用零偏置条件下像元温度响应的公式近似计算,其对应的温度偏差不大于3%。该研究为激光压制干扰红外成像系统的损伤阈值计算提供了参考。
激光辐照非制冷微测辐射热计的理论研究
Research on laser irradiation uncooled microbolometer based on finite element analysis
-
摘要: 为了研究非制冷微测辐射热计的激光损伤阈值,根据非制冷微测辐射热计的构造和成像原理,分析了像元温度响应机制,推导出了零偏置下和单次偏置时间内像元受到激光辐照的温度增量计算公式;建立了激光辐照非制冷微测辐射热计的有限元分析模型,结合实际工作条件加载热源载荷进行仿真,模拟了激光造成软损伤的过程。结果表明,激光软损伤阈值可按照零偏置条件下像元温度响应的公式近似计算,其对应的温度偏差不大于3%。该研究为激光压制干扰红外成像系统的损伤阈值计算提供了参考。Abstract: In order to study the laser damage threshold of an uncooled microbolometer, according to the construction and imaging principle of uncooled microbolometer, the temperature response mechanism of the pixel was analyzed, and the formula for calculating the temperature increment of the laser under the zero offset and single offset time was derived. A finite element analysis model of laser irradiated uncooled microbolometer was established. Simulation was carried out by loading the heat source load in combination with actual working conditions. Then the process of soft damage caused by laser was simulated. The conclusion was drawn: laser soft damage threshold approximate calculation of the pixel temperature response under zero bias conditions can be used to meet 3% accuracy. This study provides a reference for the calculation of damage threshold for laser suppression interference infrared imaging systems.
-
Key words:
- optical devices /
- damage threshold /
- finite element simulation /
- temperature response
-
Table 1. Typical parameters of UL01011 320×240 α-Si uncooled microbolometer
parameter value wavelength 8μm~14μm absorption η 80% temperature dynamic range 0K~90K thermal conductance G 1×10-7W/K heat capacity C 4×10-9J/K temperature coefficient of resistance α -0.025K-1 resistance R0 20kΩ bias resistor Rb 20kΩ bias boltage U 0.5V~3.3V Table 2. Parameters of simulation 1, 2
No. P0/W P2/(W·mm-3) ω/(rad·s-1) 1 1.6×10-6 5 0 2 7.8×10-5 10 100 Table 3. Parameters of simulation 3, 4
No. P0/W P2/(W·mm-3) ω/(rad·s-1) 3 0 0 0 4 3.4×10-6 2.5 0 Table 4. Effective simulation parameters of laser soft damage caused by laser
No. Te/K P2/(W·mm-3) ω/(rad·s-1) P0/W 5 380.69 6.3 0 1.0×10-5 6 386.32 15 50 2.5×10-5 7 382.45 27 100 4.2×10-5 -
[1] WOOD R A. Uncooled thermal imaging with monolithic silicon focal planes[J].Proceedings of the SPIE, 1993, 2020:322-329. doi: 10.1117/12.160553 [2] YU X J, ZHENG Y Ch, GUO Ch L, et al. Analysis of infrared detectability hypersonic vehicles under different background[J]. Laser Technology, 2018, 42(5): 627-632(in Chinese). [3] SUN Ch W, LU Q Sh, FAN Zh X, et al. Laser irradiation effect[M]. Beijing: National Defense Industry Press, 2002:7-12(in Ch-inese). [4] KONG L B, YI X J, WANG D H, et al. Development of 320×240 long-wave non-cooling microbolometer infrared thermal imager[J].Acta Photonics Sinica, 2002, 31(5):85-89(in Chinese). [5] FIEQUE B, TISSOT J L, TROUILLEAU C, et al. Uncooled microbolometer detector: Recent developments at ULIS[J]. Opto-Electronics Review, 2006, 14(3):187-191. [6] SUN L J. Research on performance and signal processing circuit of microbolometer array[D]. Nanjing: Nanjing University of Science and Technology, 2008: 16-36(in Chinese). [7] LENG Y P, LV J, ZHOU Y, et al. Research on non-uniformity and on-chip correction circuit of focal plane array of microbolometer[J]. Infrared, 2010, 31(12):7-11(in Chinese). [8] YANG F B. Infrared physics and technology[M]. Beijing: Publishing House of Electronics Industry, 2014:89-103(in Chinese). [9] ZHENG Y L, HU Y H, ZHAO N X, et al. Analysis of the influence of pulse width and repetition frequency on damage threshold of HgCdTe detector[J]. Laser Technology, 2018, 42(2): 265-270(in Chinese). [10] BI J, CHEN G B, JIN G Y, et al. Analytical modelling of annular millisecond laser-induced damage in silicon[J]. Lasers in Engineering (Old City Publishing), 2014, 29(3): 175-187. [11] CHEN Y, LU J, NI X, et al. Plastic penetration during laser heating of a metal plate[J]. Journal of Materials Processing Technology, 2008, 205(1/3): 9-15. [12] QIN Y, CHEN Y, NI X, et al. Axisymmetric numerical simulation of plastic damage in aluminum alloy induced by long pulsed laser[J]. Optics and Lasers in Engineering, 2010, 48(3): 361-367. doi: 10.1016/j.optlaseng.2009.10.006 [13] ZHANG J J. Research on imaging system of focal plane array of microbolometer[D]. Nanjing: Nanjing University of Science and Technology, 2006: 9-17(in Chinese). [14] RADFORD W A, MURPHY D, RAY M, et al. 320×240 silicon microbolometer uncooled IR FPAs with on-chip offset correction[J]. Proceedings of the SPIE, 1996, 2746:82-92. doi: 10.1117/12.243062 [15] TISSOT J L, CHATARD J P, FIEQUE B, et al. High performance and low thermal time constant amorphous silicon based on 320×240 uncooled microbolometer IRFPA[J]. Proceedings of the SPIE, 2004, 5640:94-99. doi: 10.1117/12.579876 -


 网站地图
网站地图

 下载:
下载: