-
正交频分复用(orthogonal frequency division multiplexing, OFDM)作为一种多载波调制技术,能够以较高的频谱利用率完善发光二极管(light emitting diode, LED)可见光窄调制带宽特性,提升可见光通信系统的通信速率[1];其所采用的正交子载波能够抵抗多径效应引起的符号干扰,提高系统可靠性[2]。但由于时域信号的叠加效应造成系统峰均比值(peak-to-average power ratio,PAPR)过高;同时双极性的复数OFDM时域信号无法应用于强度调制直接检测(intensity modulation direct detection, IM/DD)可见光通信系统中[3]。针对以上问题,吉林大学的ZHANG博士提出了基于脉冲宽度调制(pulse width modulation, PWM)的光正交频分复用(optical OFDM, O-OFDM)调制方案,通过混合调制增加系统复杂度的方法降低了系统的误比特率以及峰均比[4]。本文中将在不改变系统复杂度的前提下,通过小波多分辨率分析来进一步改善系统性能。由于小波的尺度正交和平移正交这一特性[5],使得可见光OFDM系统在抗码间干扰(inter-symbol interference, ISI)和载波间干扰(inter-carrier interference, ICI)方面有着明显优势;同时,对称结构的小波基保证了系统的线性特性[6],刚好满足OFDM正交性对线性系统的需求。
在可见光传输信道下,本文中选择Haar小波基实现可见光OFDM通信,通过对Haar小波的重构与分解,利用离散小波变换OFDM(discrete wavelet transformation OFDM, DWT-OFDM)多载波调制,提高可见光OFDM通信系统的传输效率,降低系统误比特率,抑制系统峰均比。
-
在可见光信道中,用信道损耗或者信道直流增益来描述信道的衰减特性[7],信道的直流增益H(0)定义为[8]:
$ H\left( 0 \right) = \frac{{{P_{\rm{t}}}}}{{{P_{\rm{r}}}}} $
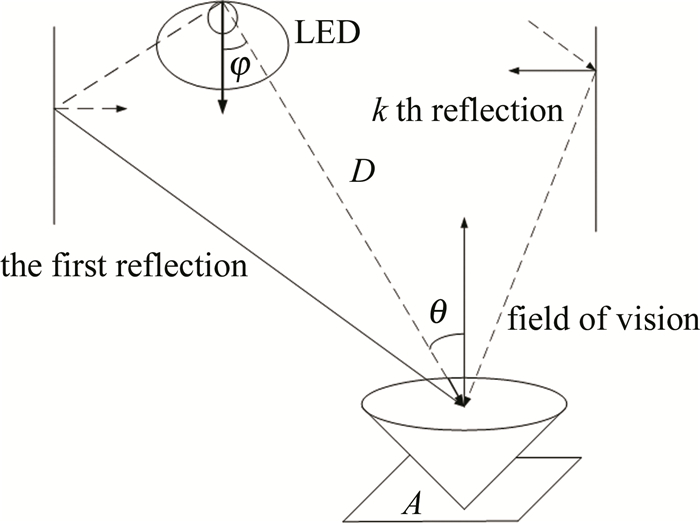
(1) 式中, Pt为发射端平均功率;Pr为接收端光平均功率。图 1所示为可见光信道通信模式[9-10]。图中,φ为发射光与光源法线之间的夹角,θ为入射光与接收端法线的夹角,A是接收器的物理面积,D为发射端与接收端之间的距离。
光接收功率为[11]:
$ {P_{\rm{r}}} = {P_{\rm{t}}}\frac{{\left( {m + 1} \right){{\cos }^m}\varphi }}{{2{\rm{ \mathsf{ π} }}{D^2}}}AT\left( \theta \right)g\left( \theta \right)\cos \theta $
(2) 系统直流增益为:
$ H\left( 0 \right) = \frac{{\left( {m + 1} \right){{\cos }^m}\varphi }}{{2{\rm{ \mathsf{ π} }}{D^2}}}AT\left( \theta \right)g\left( \theta \right)\cos \theta $
(3) 式中,m为LED朗伯辐射模型的辐射指数,T(θ)是光滤光器的增益,g(θ)是光集中器的增益。
-
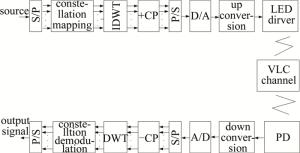
基于小波变换的OFDM系统是利用多分辨率分析的思想[12],将传统OFDM中的傅里叶变换替换为小波变换,用小波变换中的低频信息和高频信息表示信号源信号[13],选择正交小波基作为子载波,经小波逆变换后合成DWT-OFDM信号,在接收端通过小波变换恢复出原始信号,起到调制解调的作用。其系统框图如图 2所示[14]。图中,series/parallel(S/P)表示串并转换,parallel/series(P/S)表示并串转换,cyclic prefix(CP)表示循环前缀,visible light communication(VLC)表示可见光通信。
-
Haar小波是Daubechies家族中唯一一个同时具有紧支撑和对称性的正交小波[15-16],Haar小波的定义如下:
$ \psi (t) = \left\{ {\begin{array}{*{20}{l}} {1,( - 0.5 < t < 0)}\\ { - 1,(0 < t < 0.5)}\\ {0,({\rm{other}})} \end{array}} \right. $
(4) 式中,t表示时间变量。
其频域形式为:
$ \psi (\omega ) = {\rm{i}}\frac{4}{\omega }{\sin ^2}\left( {\frac{\omega }{4}} \right){{\rm{e}}^{ - \frac{{{\rm{i}}\omega }}{2}}} $
(5) 式中,ω表示频率变量,且满足正交条件[17]:
$ \left\langle {\psi \left( t \right),\psi \left( {{2^j}t} \right)} \right\rangle = 0 $
(6) 当小波经过伸缩平移后,可以得到一个小波序列[18]:
$ {\psi _{\left( {a,b} \right)}}\left( t \right) = \frac{1}{{\sqrt {\left| a \right|} }}\psi \left( {\frac{{t - b}}{a}} \right) $
(7) 式中, a, b∈R, R表示实数集; a≠0, a为尺度系数,b为平移系数。在离散化小波中,对a和b进行离散化得:a=a0j,b=ka0jb0,k, j∈Z, Z表示整数集。a0≠1, 且a0>1表示扩展步长, 为固定值。此时对应的离散小波函数ψj, k(t)可以表示为[19-20]:
$ {\psi _{j,k}}\left( t \right) = a_0^{ - j/2}\psi \left( {a_0^{ - j}t - k{b_0}} \right) $
(8) 离散小波变换系数可以表示为:
$ {C_{j,k}} = \int_{ - \infty }^{ + \infty } f (t)\psi _{j,k}^ * (t){\rm{d}}t = \left\langle {f,{\psi _{j,k}}} \right\rangle $
(9) 式中,f表示f(t)变换后的小波系数,ψ*表示ψ的复共轭。小波重构公式为:
$ f\left( t \right) = C\sum\limits_{ - \infty }^{ + \infty } {\sum\limits_{ - \infty }^{ + \infty } {{C_{j,k}}} } {\psi _{j,k}}(t) $
(10) 式中,C为与变换系数f无关的常数。
-
由于双极性的复数OFDM时域信号不适用于IM/DD的可见光通信系统中,而在DWT-OFDM系统中,不存在复值信号,采用实值小波变换,得到信号的幅值信息[21]。如图 3所示,为快速傅里叶变换OFDM(fast Fourier transformation OFDM, FFT-OFDM)与DWT-OFDM信号的实虚部波形对比图,根据对Haar小波的仿真,说明了小波函数可直接应用于IM/DD系统,降低了系统实现的复杂性。
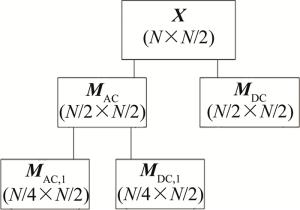
根据Haar小波重构原理,本文中定义一个DWT-OFDM信号的帧结构,如图 4所示。当信号在传输时,被分为低频信息与高频信息两部分进行传输,MAC表示低频信息矩阵,MDC表示高频信息矩阵。
根据一层Haar小波系数的分配方式,在OFDM信号帧结构当中,对数据信息进行小波系数分配,将数据信息分为低频信息MAC与高频信息MDC ,对小波进行重构,实现离散小波逆变换。
当小波变换的点数为N时,在正交Haar小波中,分解算法得到的低频信息与高频信息的矩阵模块相同。所以一层小波系数分配过程为:将原矩阵X的第1行~第N/2行矩阵中的信息作为低频信息MAC,MAC为N/2×N/2的矩阵;第(N/2+1)行~第N行矩阵中的信息作为高频信息MDC,MDC为N/2×N/2的矩阵;MAC1和MDC1是MAC中分配的低频信息矩阵与高频信息矩阵,如图 5所示。
-
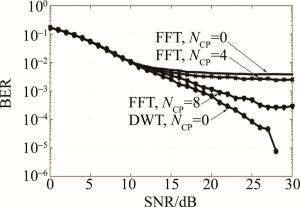
为了验证基于小波变换的可见光OFDM系统抵抗多径干扰与信道衰减的效果,采用蒙特卡洛法统计抽样,在模拟多径干扰的影响下,对FFT-OFDM和DWT-OFDM通信系统性能进行MATLAB仿真。在DWT-OFDM系统中,采用Haar小波一层重构分解技术,在发送端采用逆离散小波变换(inverse discrete wavelet transformation, IDWT)小波重构,在接收端采用DWT小波分解。在FFT-OFDM系统中,采用不同循环前缀NCP,对比DWT-OFDM系统的误比特率。
仿真参量如下:子载波个数为64,系统采用BPSK调制。仿真结果如图 6所示。
由仿真结果分析可以得出,在FFT-OFDM系统中,随着循环前缀个数的增加,系统的误比特率随之降低,同时会引起传输效率的降低,而当循环前缀达到一定阈值时,系统的误比特率将趋于平缓。当误比特率为10-3时,DWT-OFDM系统较循环前缀个数为8的FFT-OFDM系统误码性能提高了2dB,通信效率提高了11%;当误比特率为10-4时,DWT-OFDM系统较循环前缀为8的FFT-OFDM系统误码性能大约提高了5dB,通信效率提高了约11%。在信噪比为27dB时,DWT-OFDM系统的误比特率可降至约10-5量级。
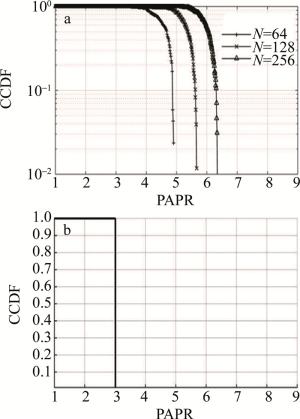
在子载波个数N分别为64,128,256,仿真周期为256时, FFT-OFDM系统的循环前缀为8,DWT-OFDM系统的循环前缀为0,仿真对比其互补累计分布函数(complementary cumulative distribution function, CCDF)值,如图 7所示。图 7a为FFT-OFDM不同子载波峰均比曲线对比, 图 7b为DWT-OFDM峰均比曲线。
当系统的子载波为Haar小波时,由于Haar小波的时域不连续性,满足整数移位正交特性;又因为Haar小波的对称性使信号传输不会产生相位畸变,更好地保留了相位信息;且因其较好的正则性,重构系数稳定,易于获得光滑的重构曲线,故不会产生较高的PAPR值。
-
为了提高可见光系统的通信性能,降低系统误比特率,提高系统的通信效率,本文中将小波变换引入可见光通信系统中,应用Haar小波基的重构与分解,将传输信息分为低频与高频信息进行传输,从而减少误差降低系统的误比特率,抑制了高峰均比的产生。通过仿真实验可以得出:在相同条件信道传输下,DWT-OFDM系统的可靠性较FFT-OFDM系统提高了5dB,传输效率有所提高,高峰均比得到了抑制。通过在可见光系统中加入小波变换,仿真了其通信的可行性,优化了可见光通信系统的性能。
基于小波变换的可见光OFDM通信系统性能优化
Performance optimization of visible light OFDM communication system based on wavelet transform
-
摘要: 在可见光通信中, 由于信道的多径效应和信道衰减在传统正交频分复用(OFDM)系统会产生符号间干扰, 从而降低系统的可靠性。为了保障通信质量, 采用带有循环前缀的OFDM系统来抵抗多径效应引起的符号干扰; 为了降低系统的误比特率和峰均比, 采用Haar小波来实现系统有效性、可靠性、峰均比等参量的性能优化, 并采用蒙特卡洛法进行了仿真验证。结果表明, 当系统的误比特率为10-4时, 离散小波变换OFDM系统较快速傅里叶变换OFDM(FFT-OFDM)系统的误码性能大约提高了5dB, 通信效率提高了大约11%;当系统的峰均比为5dB时, FFT-OFDM系统的互补累计分布函数(CCDF)值接近10-2, DWT-OFDM系统的CCDF值为0。该研究为可见光小波变换OFDM通信提供了参考。Abstract: In visible light communications, multipath effects and channel attenuation in traditional orthogonal frequency division multiplexing (OFDM) systems can generate intersymbol interference and reduce system reliability. In order to guarantee the quality of communication, OFDM system with cyclic prefix was used to resist the symbolic interference caused by multipath effect. In order to reduce bit error rate(BER) and peak-to-average power ratio(PAPR) of the system, Haar wavelet was used to optimize the performance of system parameters such as validity, reliability and PAPR. Monte Carlo method was used to verify the simulation results. The results show that, when bit error rate of the system is 10-4, BER performance of discrete wavelet transform OFDM system is about 5dB higher than that of fast Fourier transform OFDM (FFT-OFDM) system. Communication efficiency has been improved by about 11%. When PAPR of the system is 5dB, complementary cumulative distribution function (CCDF) of FFT-OFDM system is close to 10-2. CCDF value of DWT-OFDM system is 0. This study provides a reference for OFDM communication based on visible light wavelet transform.
-
[1] HU W W. PAPR reduction in DCO-OFDM visible light communication systems using optimized odd and even sequences combination[J]. IEEE Photonics Journal, 2019, 11(1):1-16. [2] CAI S, LI C, WANG W. Design and experiments of an adaptive OFDM system for visible light communication[J]. Journal of University of Chinese Academy of Sciences, 2018, 35(1):137-143. [3] KE X Zh, KANG Y, LIU J. Experimental research on PAPR reduction algorithms in FSO-OFDM system[J]. Infrared and Laser Engineering, 2017, 46(6):173-179(in Chinese). [4] ZHANG T. The key technology research of indoor visible light communications based on OFDM[D]. Changchun: Jilin University, 2016: 88-110(in Chinese). [5] ZHAO H B, ZHANG D, YANG J K, et al. Application of wavelet layered method for laser Doppler velocimetry signal[J]. Laser Technology, 2019, 43(1):103-108(in Chinese). [6] NAN R Z, WEI M X H, RU H W, et al. Imperceptible digital watermarking scheme in multiple transform domains[J]. Multimedia Tools & Applications, 2018, 77(23):30251-30267. [7] KIM B W. Suboptimal LED selection for distributed MIMO visible light communications[J]. Personal & Ubiquitous Computing, 2018, 22(4):1-6. [8] SUN Z G, YU H Y, TIAN Z J, et al. Linear precoding for MU-MISO VLC systems with noisy channel state information[J]. IEEE Communications Letters, 2018, 22(4):732-735. doi: 10.1109/LCOMM.2018.2795025 [9] LIU Zh G, ZHAO L, ZHU T, et al. Research of indoor positioning and illuminating systems based on visible light[J]. Laser Technology, 2018, 42(5):646-650(in Chinese). [10] DING D Q, KE X Zh. Visible light communication and research on its key techniques[J]. Semiconductor Optoelectronics, 2006, 27(2):114-117(in Chinese). [11] JIANG X M, ZHU X Y, LIU T, et al. Design and implementation of LED indoor visible light voice communication system[J]. Laser Technology, 2014, 38(6):807-812(in Chinese). [12] LIU W, SHANG Q F. 2-D lifting wavelet de-noising method for Rayleigh BOTDA system[J]. Laser Technology, 2018, 42(3):346-350(in Chinese). [13] WANG T, SHEN Y H, YAO J Q. Research on laser radar echo signal denoising based on wavelet threshold method[J]. Laser Technology, 2019, 43(1):63-68(in Chinese). [14] KE X Zh. Principle and application of orthogonal frequency division multiplexing in wireless optical communication[M]. Beijing: Science Press, 2018:146-153(in Chinese). [15] LI F, MAO Q, CHANG C C. Reversible data hiding scheme based on the Haar discrete wavelet transform and interleaving prediction method[J]. Multimedia Tools & Applications, 2018, 77(5):5149-5168. [16] ZHANG C Y, LI J B, WANG S S, et al. Encrypted image retrieval algorithm based on discrete wavelet transform and perceptual hash[J]. Journal of Computer Applications, 2018, 38(2):539-544. [17] ARIVUDAINAMBI D, BALAJI S, SRIPATHY B, et al. Enhancing quality of coverage for target coverage problem using discrete haar wavelet[J]. Wireless Personal Communications, 2018, 101(3):1-21. [18] CALDERóN-RICO R, CARRASCO-ALVAREZ R, CASTILLO J V. Dynamic wavelet-based pilot allocation algorithm for OFDM-based cognitive radio systems[J]. Telecommunication Systems, 2018, 68(2):193-200. doi: 10.1007/s11235-017-0386-0 [19] ZENG J Q, WANG J, CHEN Y, et al. Multiple-color-image compression and encryption by using discrete wavelet transform in Fresnel transform in Fresnel transform domain[J]. Laser Technology, 2018, 42(6):733-738(in Chinese). [20] ARGOUL F, ARNEODO A, ELEZGARAY J, et al. Wavelet transform of fractal aggregates[J]. Physics Letters, 2017, A135(6):327-336. [21] KE X Zh, ZHANG Q W. Experimental study on FSO-WOFDM system[J]. Infrared and Laser Engineering, 2018, 47(10):247-253(in Chinese). -


 网站地图
网站地图

 下载:
下载: