-
近年来,随着我国煤矿开采能力不断提高,常规的巷道掘进技术已无法满足需求[1],对矿下掘进机的工作效率提出了更高的要求。实现自动化和无人化是提高掘进机工作效率的重要发展方向[2],而精确的导航定位技术是实现掘进自动化的关键[3]。
目前煤矿井下,掘进机推进方向依赖激光指向仪打在掌子面上的光斑[4],可靠性不高且易受现场粉尘等不良因素影响。国内针对掘进机位姿测量的问题已经有了许多研究成果。YUAN[5]提出了一种基于室内空间定位技术的掘进机位姿测量方法,测量精度高, 但是需要加以改进以适应掘进机工作环境[6]。WU[7]等人提出了一种基于空间交汇测量技术的掘进机位姿测量方法,灵活性好但可靠性差[6]。视觉测量技术具有结构简单、测量精度高及测量范围广等优点[8],TIAN[9],DU等人[10]基于该技术提出两种方法,可以实现掘进机位姿测量,但是易受工况环境中的震动影响。此外, HUANG等人[11]提出了一种将视觉测量与捷联惯性导航技术结合起来的测量方法,有效改善了惯性导航系统测量结果随时间发散的情况,但该方法只能得到掘进机的五自由度信息。
以上测量方法各有其优势和不足,为进一步提高掘进机位姿测量的准确性和全面性,本文中提出了一种基于空间矢量约束的测量方法,将测偏单元、激光指向仪光源光斑和照射到掌子面上的光斑构成空间四边形,结合视觉测量和惯性导航技术建立空间矢量约束方程,可以实现煤矿掘进机六自由度测量。
-
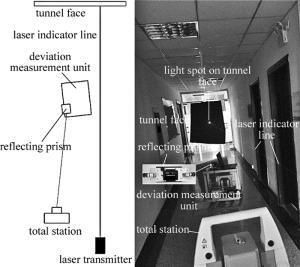
测量原理如图 1所示。测偏单元由一组反向同轴安装的工业相机和捷联惯导构成。
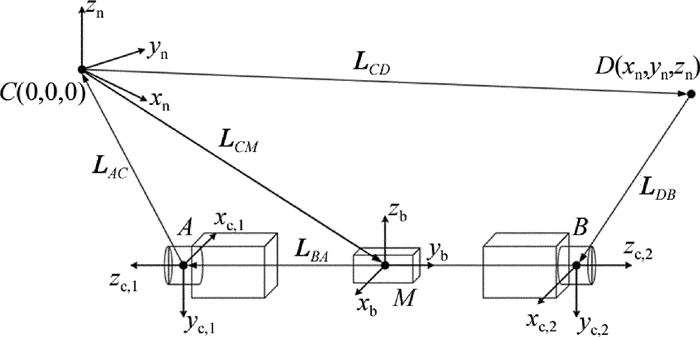
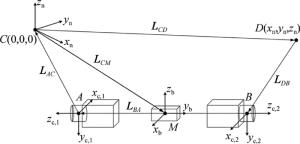
其中涉及几个坐标系:导航坐标系C-xnynzn(x, y, z的指向依次为东、北、天),惯导载体坐标系M-xbybzb以及两个相机坐标系A-xc, 1yc, 1zc, 1和B-xc, 2yc, 2zc, 2,且相机A和B所在相机坐标系的zc, 1, zc, 2轴与惯导载体坐标系yn轴重合,即3个坐标系原点A,M,B共线。图中C点表示激光指向仪光源点,D点表示激光指向仪照射在掌子面上的光点,$\overrightarrow {CD} , \overrightarrow {DB} , \overrightarrow {BA} , \overrightarrow {AC} $ 4个空间矢量首尾相连,构成封闭的空间四边形,若在导航坐标系下分别表示为LCD, LDB, LBA, LAC,则有:
$ {\mathit{\boldsymbol{L}}_{CD}} + {\mathit{\boldsymbol{L}}_{DB}} + {\mathit{\boldsymbol{L}}_{BA}} + {\mathit{\boldsymbol{L}}_{AC}} = 0 $
(1) (1) 式可变形为:
$ \begin{array}{*{20}{c}} {\left| {{\mathit{\boldsymbol{L}}_{CD}}} \right| \cdot {\mathit{\boldsymbol{e}}_{CD}} + \left| {{\mathit{\boldsymbol{L}}_{DB}}} \right| \cdot {\mathit{\boldsymbol{e}}_{DB}} + \left| {{\mathit{\boldsymbol{L}}_{AC}}} \right| \cdot {\mathit{\boldsymbol{e}}_{AC}} = }\\ { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA}}} \end{array} $
(2) 式中,eCD,eDB,eBA,eAC表示导航坐标系下的单位矢量; |LCD|,|LDB|,|LBA|,|LAC|表示相应矢量的模值。(2)式中变量均为3维矢量,所以可表示为以|LCD|,|LDB|,|LAC|为变量的三元一次方程组:
$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_{CD,x}}}&{{\mathit{\boldsymbol{e}}_{DB,x}}}&{{\mathit{\boldsymbol{e}}_{AC,x}}}\\ {{\mathit{\boldsymbol{e}}_{CD,y}}}&{{\mathit{\boldsymbol{e}}_{DB,y}}}&{{\mathit{\boldsymbol{e}}_{AC,y}}}\\ {{\mathit{\boldsymbol{e}}_{CD,z}}}&{{\mathit{\boldsymbol{e}}_{DB,z}}}&{{\mathit{\boldsymbol{e}}_{AC,z}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\left| {{\mathit{\boldsymbol{L}}_{CD}}} \right|}\\ {\left| {{\mathit{\boldsymbol{L}}_{DB}}} \right|}\\ {\left| {{\mathit{\boldsymbol{L}}_{AC}}} \right|} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,x}}}\\ { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,y}}}\\ { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,z}}} \end{array}} \right]} \end{array} $
(3) 整理可得:
$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\left| {{\mathit{\boldsymbol{L}}_{CD}}} \right|}\\ {\left| {{\mathit{\boldsymbol{L}}_{DB}}} \right|}\\ {\left| {{\mathit{\boldsymbol{L}}_{AC}}} \right|} \end{array}} \right] = {{\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_{CD,x}}}&{{\mathit{\boldsymbol{e}}_{DB,x}}}&{{\mathit{\boldsymbol{e}}_{AC,x}}}\\ {{\mathit{\boldsymbol{e}}_{CD,y}}}&{{\mathit{\boldsymbol{e}}_{DB,y}}}&{{\mathit{\boldsymbol{e}}_{AC,y}}}\\ {{\mathit{\boldsymbol{e}}_{CD,z}}}&{{\mathit{\boldsymbol{e}}_{DB,z}}}&{{\mathit{\boldsymbol{e}}_{AC,z}}} \end{array}} \right]}^{ - 1}} \cdot }\\ {\left[ {\begin{array}{*{20}{c}} { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,x}}}\\ { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,y}}}\\ { - \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA,z}}} \end{array}} \right]} \end{array} $
(4) 式中,eBA, |LBA|分别表示测偏单元的方向矢量和物理长度;eCD, |LCD|表示激光指示线的方向矢量和物理长度。
惯导模块可以输出载体的3个姿态角,即θ, γ, φ,并且构造出载体坐标系b系到导航坐标系n系的转换矩阵Cbn[12]:
$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}} = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi }&0\\ {\sin \varphi }&{\cos \varphi }&0\\ 0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \theta }&{ - \sin \theta }\\ 0&{\sin \theta }&{\cos \theta } \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&0&{\sin \gamma }\\ 0&1&0\\ { - \sin \gamma }&0&{\cos \gamma } \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos \gamma \cos \varphi - \sin \gamma \sin \theta \sin \varphi }&{ - \cos \theta \sin \varphi }&{\sin \gamma \cos \varphi + \cos \gamma \sin \varphi \sin \theta }\\ {\sin \varphi \cos \gamma + \sin \gamma \sin \theta \cos \varphi }&{\cos \theta \cos \varphi }&{\sin \gamma \sin \varphi - \cos \gamma \sin \theta \cos \varphi }\\ { - \sin \gamma \cos \theta }&{\sin \theta }&{\cos \gamma \cos \theta } \end{array}} \right]} \end{array} $
(5) eBA可表示为:
$ {\mathit{\boldsymbol{e}}_{BA}} = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}} \cdot \mathit{\boldsymbol{e}}_{BA}^{\rm{b}} $
(6) 由于LBA与载体坐标y系轴重合,故eBAb=[0-1 0]T,计算可得:
$ {\mathit{\boldsymbol{e}}_{BA}} = {\left[ {\cos \theta \sin \varphi \quad - \cos \theta \cos \varphi \quad - \sin \theta } \right]^{\rm{T}}} $
(7) (4) 式中的eAC,eBD表示在导航坐标系下激光指向仪的光源光斑和照射到掌子面上的光斑分别投影在两个相机像平面上的单位光束矢量,设两个相机得到的光斑在像素坐标系下的位置(uAC, vAC)和(uDB, vDB),通过相机成像原理中的坐标系关系[13-14]得到:
$ {z_{\rm{c}}}\left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{\lambda }{{{d_x}}}}&0&{{u_0}}\\ 0&{\frac{\lambda }{{{d_y}}}}&{{v_0}}\\ 0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{x_{\rm{c}}}}\\ {{y_{\rm{c}}}}\\ {{z_{\rm{c}}}} \end{array}} \right] $
(8) 式中,u, v表示光斑在像素坐标系下的坐标;λ为相机的焦距;dx和dy分别是每个像素在像平面的x轴和y轴方向上的物理尺寸;(u0, v0)是图像坐标系原点在像素坐标系中的坐标;像平面上的点在相机坐标系下z轴方向坐标均为焦距的值,整理可得:
$ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{c}}} = \left( {u - {v_0}} \right) \times {d_x}}\\ {{y_{\rm{c}}} = \left( {v - {v_0}} \right) \times {d_y}}\\ {{z_{\rm{c}}} = \lambda } \end{array}} \right. $
(9) 通过求得的两个光斑在相机坐标系下的位置(xc, 1, yc, 1, zc, 1)和(xc, 2, yc, 2, zc, 2),可计算出单位矢量eACb, eBDb,进而eAC, eDB可表示为:
$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_{AC}} = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}} \cdot \mathit{\boldsymbol{C}}_{{\rm{c}},1}^{\rm{b}} \cdot \mathit{\boldsymbol{e}}_{AC}^{c,1}}\\ {{\mathit{\boldsymbol{e}}_{DB}} = - \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}} \cdot \mathit{\boldsymbol{C}}_{{\rm{c}},2}^{\rm{b}} \cdot \mathit{\boldsymbol{e}}_{BD}^{{\rm{c}},2}} \end{array}} \right. $
(10) 式中,Cbn在前面已经求得,Cc, 1b和Cc, 2b分别表示两个相机坐标系到惯导载体坐标系的旋转矩阵,可通过测偏单元的工装和初始标定获得,以Cc, 1b为例进行说明。
根据如图 2所示的相机坐标系与惯导载体坐标系关系,可利用(5)式得到旋转矩阵Cc, 1b的表达式:
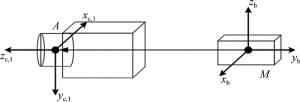
Figure 2. Relationship between camera coordinate system and inertial navigation carrier coordinate system
$ \mathit{\boldsymbol{C}}_{{\rm{c}},1}^{\rm{b}} = \left[ {\begin{array}{*{20}{c}} {\cos b\cos c - \sin b\sin a\sin c}&{ - \cos a\sin c}&{\sin b\cos c + \cos b\sin c\sin a}\\ {\sin c\cos b + \sin b\sin a\cos c}&{\cos a\cos c}&{\sin b\sin c - \cos b\sin a\cos c}\\ { - \sin b\cos a}&{\sin a}&{\cos b\cos a} \end{array}} \right] $
(11) 式中,a,b,c表示相机坐标系绕其x,y,z轴旋转的角度,工装后标定得到。
至此(4)式中等式右边变量全部求得,进而可以得到|LCD|,|LDB|,|LAC|的值,对于图 1中的△ACM,有$\overrightarrow {CM} = \overrightarrow {CA} + \overrightarrow {AM} $,展开得:
$ \begin{array}{*{20}{c}} {\overrightarrow {CM} = \left| {{\mathit{\boldsymbol{L}}_{AC}}} \right| \cdot {\mathit{\boldsymbol{e}}_{CA}} + \left| {{\mathit{\boldsymbol{L}}_{AM}}} \right| \cdot {\mathit{\boldsymbol{e}}_{AM}} = }\\ { - \left| {{\mathit{\boldsymbol{L}}_{AC}}} \right| \cdot {\mathit{\boldsymbol{e}}_{AC}} + \frac{1}{2} \times \left| {{\mathit{\boldsymbol{L}}_{BA}}} \right| \cdot {\mathit{\boldsymbol{e}}_{BA}}} \end{array} $
(12) C点是导航坐标系的原点,所以空间矢量$\overrightarrow {CM} $的值就是M点的空间坐标,即测偏单元在导航坐标系n系下的3维坐标,结合捷联惯导输出的姿态信息,最终实现对掘进机位姿的六自由度测量。
-
为验证位姿测量方法的可行性,在实验室环境下进行实验,本次实验设备如表 1所示。表中H和V分别表示水平方向和垂直方向的分辨率,F是光圈值。
Table 1. Experimental equipment for pose measurement
No. name performance and parameters 1 camera resolution(H×V):1280pixel×1024pixel
chip size:6.8mm×5.4mm
pixel size:5.3mm×5.3mm2 prime lens focal length:16mm
F:1.4~16
aberration rate:0.1%
specification:(2/3)″
viewing angle:38.0°×30.8°×23.4°3 MEMS-INS dynamic accuracy:≤0.1°
zero-bias stability:≤5°/h
range:±300°/s or ±130°/s
bias repeatability:≤36°/h4 total station display resolution:0.1mm
measurement accuracy:1mm
measurement range:2000m实验步骤见下。
(1) 根据相机相关标定方法[15-16]计算出相机内参矩阵为:
$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{M}}_A} = \left[ {\begin{array}{*{20}{c}} {3047.6528}&0&{653.9029}\\ 0&{3045.0165}&{567.5144}\\ 0&0&1 \end{array}} \right]\\ {\mathit{\boldsymbol{M}}_{\rm{B}}} = \left[ {\begin{array}{*{20}{c}} {3035.3679}&0&{637.8389}\\ 0&{3027.3200}&{496.5051}\\ 0&0&1 \end{array}} \right] \end{array} \right. $
(13) (2) 组装测偏单元,保证两个相机坐标系的z轴与MEMS-INS坐标系的y轴重合,且坐标系都满足右手定则,反射棱镜与基于微机电技术的惯性导航系统(micro electro mechanical systems-inertial navigation system,MEMS-INS)刚性连接,整体安装效果如图 3所示。
(3) 搭建测试环境:首先在测试终点用黑布模拟掌子面,激光发射器安装在起点并照射掌子面,光线呈水平,激光指示线全长约10m;其次将组装好的测偏单元固定在可移动测偏平台上,MEMS-INS所示的yn轴方向与测偏平台前进方向一致;然后将全站仪固定在起点附近,然后调平并按照MEMS-INS的导航坐标系设站;最后测试平台初始位置设置在激光线的中间。位姿测量实验环境如图 4所示。
(4) 任意方向移动测偏平台,同时保证相机可以采到光斑,停止时记录上位机计算出的测偏单元位姿信息,并用全站仪测量反射棱镜坐标,分别在表 2和表 3中给出。
Table 2. Position information measured by deviation measurement unit
No. x axis/m y axis/m z axis/m euclidean distance between adjacent points/m 1 -1.0753 0.0152 -0.1293 — 2 -4.5749 -0.028 -0.5060 3.52008 3 -3.7289 -0.1182 -0.3877 0.85898 4 -2.0196 -0.0310 -0.1594 1.72668 5 -0.4934 -0.0014 -0.0507 1.53035 Table 3. Position information measured by total station instrument
No. x axis/m y axis/m z axis/m euclidean distance between adjacent points/m 1 -2.8244 0.6297 -0.2236 — 2 -3.2589 0.5614 -0.2242 0.43984 3 -3.3421 0.5753 -0.2247 0.08436 4 -3.812 0.6221 -0.2278 0.47224 5 -3.812 0.6221 -0.2278 0 通过比较测偏单元与全站仪测量结果中对应的相邻欧式距离可得测偏单元测量的误差,因为与激光计划线长度相比,测偏单元物理长度过小,导致计算得出的空间矢量有误差,从而影响位置结果精度。其中表 2和表 3中的第4条和第5条记录,全站仪测得测偏单元处于静止状态,但是测偏单元测出的位置是在变化的,分析是由于该时刻测偏单元方向矢量与激光线平行,(6)式中4个空间矢量组成的空间四边形成为平行四边形,所以在只知道一条边的长度和4条边的方向矢量的前提下,其余3条边长度有无穷解。实验结果表明,除了上述特殊情况,在两个相机可采到对应光点光斑的情况下,可以得到测偏单元在MEMS-INS的导航坐标系下的位置姿态信息,且该坐标信息的误差不随时间发散,同时测偏单元姿态信息由MEMS-INS单独提供,不受其它条件影响。
-
为了研究基于空间矢量约束方法来解决掘进机位姿测量问题的可行性,在可以一定程度上解决纯惯性导航系统位置误差随时间快速发散的问题,通过实验也验证该方法可以实现掘进机位姿的六自由度测量。下一步的研究重心将放在如何提高精度以及如何应对位姿测量实验中出现的特殊情况。
基于空间矢量约束的煤矿掘进机组合测量方法
Combination measurement method of coal mine roadheaders based on space vector constraint
-
摘要: 为了解决煤矿掘进机位姿测量的问题, 将一组反向同轴安装的工业相机和捷联惯性导航系统组装成测偏单元, 并结合视觉测量和惯性导航技术提出了一种基于空间矢量约束的实时位姿组合测量方法。该方法通过测偏单元测得激光指向仪光源光斑的空间矢量、掌子面光斑的空间矢量和掘进机的姿态信息, 建立空间矢量约束方程以及坐标系转换得到掘进机位置信息, 并进行了理论分析和实验验证。结果表明, 通过该方法能得到掘进机实时位姿的六自由度信息。该方法可用于煤矿掘进机的位姿测量, 具有广阔的应用和发展前景。Abstract: In order to solve the problem of measuring the position and posture of a coal mine roadheader, a set of reverse coaxial industrial cameras and strapdown inertial navigation system were assembled into a bias measurement unit. Combining vision measurement and inertial navigation technology, a real-time pose measurement method was proposed based on space vector constraints. In this method, the spatial vector of the light spot of laser pointer, the spatial vector of the light spot of palm face and the attitude information of roadheader were measured by the deviation measuring unit. Space vector constraint equation and coordinate system conversion were established. The location information of the roadheader was obtained. Theoretical analysis and experimental verification were carried out. The results show that, the six degrees of freedom information of the real-time position and posture of the roadheader can be obtained by this method. This method can be used to measure the position and posture of coal mine roadheaders, and has broad application and development prospects.
-
Key words:
- measurement and metrology /
- roadheader /
- vision measurement /
- inertial navigation /
- space vector
-
Table 1. Experimental equipment for pose measurement
No. name performance and parameters 1 camera resolution(H×V):1280pixel×1024pixel
chip size:6.8mm×5.4mm
pixel size:5.3mm×5.3mm2 prime lens focal length:16mm
F:1.4~16
aberration rate:0.1%
specification:(2/3)″
viewing angle:38.0°×30.8°×23.4°3 MEMS-INS dynamic accuracy:≤0.1°
zero-bias stability:≤5°/h
range:±300°/s or ±130°/s
bias repeatability:≤36°/h4 total station display resolution:0.1mm
measurement accuracy:1mm
measurement range:2000mTable 2. Position information measured by deviation measurement unit
No. x axis/m y axis/m z axis/m euclidean distance between adjacent points/m 1 -1.0753 0.0152 -0.1293 — 2 -4.5749 -0.028 -0.5060 3.52008 3 -3.7289 -0.1182 -0.3877 0.85898 4 -2.0196 -0.0310 -0.1594 1.72668 5 -0.4934 -0.0014 -0.0507 1.53035 Table 3. Position information measured by total station instrument
No. x axis/m y axis/m z axis/m euclidean distance between adjacent points/m 1 -2.8244 0.6297 -0.2236 — 2 -3.2589 0.5614 -0.2242 0.43984 3 -3.3421 0.5753 -0.2247 0.08436 4 -3.812 0.6221 -0.2278 0.47224 5 -3.812 0.6221 -0.2278 0 -
-


 网站地图
网站地图

 下载:
下载: