-
信息化盛行的时代,信号的检测与分析对通信领域起到了重要的作用,这包含了信号各种参量的测量,如频率、幅度和相位等。其中,频率信息能够显示出信号的调制特性,为后续的信号处理打下扎实的基础[1-4]。过去,使用电子学的方法实现微波信号的测频虽然可以得到较高的精度和较大的动态范围,但是因为“电子瓶颈”等不可避免的因素,使得测量范围往往只处于0.5GHz~18GHz。由于科技的发展,待测信号的频率通常达到更高的范围内,原先的电子学测量方法就不能满足现阶段的情况[5-7]。基于光子学的微波信号频率测量技术可以在宽频率覆盖、低频依赖损耗和对电磁干扰的强抗扰性等方面都能实现卓越的性能[8-10]。在目前的测频领域中,微波光子测频技术被人们广泛研究与使用,体现了其具有非常高的研究价值。
本文中提出一种基于相位调制与强度调制相结合的微波频率测量技术,可以在光纤中根据色散引起微波功率损耗,从而获得单调变化的频率-幅度映射关系,并通过幅度比较函数(amplitude comparison function,ACF)来测量微波信号的频率。该仿真方案的测频范围可以达到0.5GHz~53GHz,且测量误差仅小于±200MHz。另外,本文中通过理论分析与模拟仿真的结合,进一步实现测频范围与测频精确度的优化。
-
近年来国内外进行了多种关于微波测频的研究并取得了显著的研究成果。通过调研可以将这些技术大致分为3类:第1类是通过时间参量进行测频研究,根据测量光载波的两个边带经过一段光纤后产生的时延差大小来实现频率值的测量[11],这种方案能够同时测量两个不同的微波信号,但是该技术由于高速示波器和脉冲信号发生器的限制使得测量范围小,且测量误差超过1GHz,所以并不适用;第2类是通过空间参量进行测频研究,当光载波通过特殊的光学通道时,可以依据其经过不同种光学通道来实现测频,光学通道可以是啁啾布喇格光栅[12]、自由空间衍射光栅[13]、集成波导滤波器[14]或光栅和棱镜的组合[15]等,但是该技术由于器件需要经过特殊设计和加工工艺,导致测量系统成本昂贵,并且测量误差超过800MHz,所以并不适用;第3类是通过频率与功率的关系来进行测频研究,这是目前光子学测频技术的研究方向[16-18]。其中这里需要用到ACF[19-21],通过微波功率损耗所产生的比值函数进行测频,其测量精度可以降至400MHz,且通过光子滤波器[22]、保偏光纤和高色散光纤组合[23]、双边带载波抑制调制[24]等方式,可以实现在低中部频段内测量误差小的特点,克服测量不稳定性的缺点,在实时测频方向上搭建了一种低成本、高精度的解决方案。
-
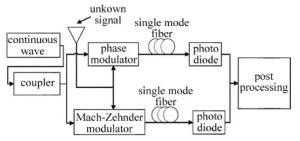
图 1所示的是基于光子技术的测频仿真结构图。该系统采用的是波长为1550nm的连续波(conti-nuous wave,CW)光源,经过耦合器将入射光分成上下两部分,把未知频率的微波信号分别通过相位调制器(phase modulator,PM)和马赫-曾德尔调制器(Mach-Zehnder modulator,MZM),之后将调制后的信号经过两段长距离的单模光纤(single mode fiber,SMF),其中光纤中的色散值为34ps/nm,根据色散引起的功率损耗的特点,可以得到单调变化的频率-幅度的映射关系,最后通过光电探测器(photo diode,PD)的输出信号功率比来得到ACF,进而实现微波测频。
对于上臂中强度调制(intensity modulation, IM)所产生的双边带(double sideband,DSB)光信号,频率响应是低通的,而对于下臂中相位调制所产生的DSB光信号,频率响应是带通的。因此,两个PD输出处的输出功率分别如下式所示[25]:
$ {P_{{\rm{IM}}}} = {R_1}{\cos ^2}\left( {\frac{{\pi D{L_1}{\lambda _{\rm{c}}}^2{f^2}}}{c}} \right) $
(1) $ {P_{{\rm{PM}}}} = {R_2}{\sin ^2}\left( {\frac{{\pi D{L_2}{\lambda _{\rm{c}}}^2{f^2}}}{c}} \right) $
(2) 式中,f是指未知微波信号的频率,Li(i=1,2)是指方案中上下部分的SMF长度,D是指SMF的色散系数,λc和c分别是指光载波的波长和光速常量,Ri(i=1,2)是指方案上下臂中包括耦合器、调制器、SMF和PD的总损耗。
根据PD探测所得的上下臂功率的比值为rACF,表达式如下所示[25]:
$ {r_{{\rm{ACF}}}} = \frac{{{R_2}{{\sin }^2}\left( {\frac{{\pi D{L_2}{\lambda _{\rm{c}}}^2{f^2}}}{c}} \right)}}{{{R_1}{{\cos }^2}\left( {\frac{{\pi D{L_1}{\lambda _{\rm{c}}}^2{f^2}}}{c}} \right)}} $
(3) 可以看出,该函数所反映的频率与功率的映射关系是非线性的,这对构建ACF有较大的难度。为了解决这一难题,可以进一步简化该非线性函数,通过校准和处理,将R1=R2,并且在方案中将上下臂的SMF长度保持一致,同时设置为L=2km,从而将ACF转换成下式[25]:
$ {r_{{\rm{ACF}}}} = {\tan ^2}\left( {\frac{{\pi DL{\lambda _{\rm{c}}}^2{f^2}}}{c}} \right) $
(4) 这样就可以构建出更为简化的ACF函数,从而方便通过计算来得到未知微波信号的频率。
-
本文中采用VPI Transmission Maker 8.6光学仿真软件来实现微波测频方案中的搭建、仿真和分析等工作,该软件由一个强大的图形界面、一个复杂且稳定的仿真调度程序和大量逼真的仿真模型组成。经过对该仿真软件进行一系列相关类型的仿真分析与实验对比,可以证实该仿真软件所得到的数据结果是具有可靠性的。
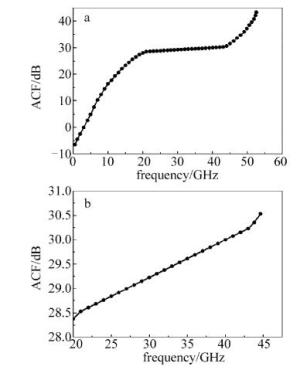
图 2a所示为仿真得到的ACF图像。可以发现,根据单调变化的频率-幅度的映射关系,能够获得未知微波信号的频率。其中,此仿真方案的测频范围可以达到0.5GHz~53GHz,根据常用的光功率计在测量精度方面的定义,光功率计的灵敏度为每吉赫兹的频率变化所引起的ACF的变化量,当灵敏度大于0.03dB/GHz时,常用的光功率计可以完成准确测频[26],虽然ACF图像在20GHz~45GHz的中间部分较为平坦,经过对该频段进行放大,如图 2b所示,可以看出,ACF图像在该频段上呈现单调上升的趋势,且满足光功率计灵敏度大于0.03dB/GHz的特点,仍然可以通过对ACF图像一一对应的测量方式来实现测频。接下来将进一步通过仿真分析来实现测频范围与测频精确度的优化。
-
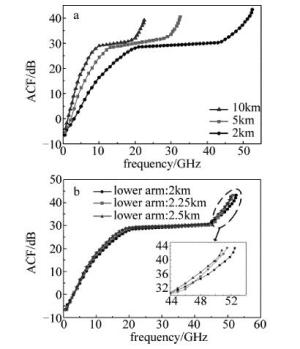
图 3a所示的是不同长度SMF(两路光纤长度相等)下的ACF图像。当SMF长度为2km, 5km和10km时,所对应的测频范围分别可以达到23GHz, 33GHz和53GHz。能够看出,随着SMF长度的增大,会导致测频范围的缩小,则测频范围与SMF长度有着一定的关系,通过适当缩小SMF的长度, 可以有效地扩大测频范围。
图 3b所示的是不同长度SMF(两路光纤长度不等)下的ACF图像。当上臂SMF长度为2km,设置下臂SMF长度分别为2km, 2.25km和2.5km,所对应的测频范围分别可以达到53GHz, 52GHz和51GHz。其中,当上下臂长度不等且变化率达到25%时,测频范围的变化率只有3.8%,能够看出, 上下臂SMF的长度不等会引起测频范围发生相应的变化,但是变化程度并不明显,所以仍然可以较好地实现测频。
-
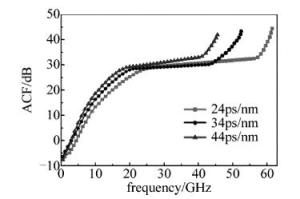
图 4所示的是在不同色散情况下的ACF图像。当色散值为24ps/nm, 34ps/nm和44ps/nm时,所对应的测频范围分别可以达到61GHz, 53GHz和46GHz。能够看出, 光纤中色散的增大会引起测频范围的缩小,则测频范围与光纤中的色散值有关,可以适当减小色散值从而有效地扩大测频范围。
-
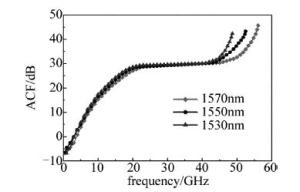
图 5所示的是不同光载波波长下的ACF图像。当光载波波长为1530nm, 1550nm和1570nm时,所对应的测频范围分别能够达到49GHz, 53GHz和56GHz。能够看出, 光载波波长的增大会引起测频范围的增大,则测频范围与光载波波长有关,可以适当增大光载波波长从而有效地扩大测频范围。
-
由于光纤中色散所引起微波功率损耗的特点,根据单调变化的频率-幅度的映射关系,可以通过ACF来进行微波测频。在多频测量方面,可以将多种不同频率的微波信号同时引入到该方案中,再经过PD的输出端进行后期处理从而同时得到多个点,最后根据ACF图像对相应的各点进行一一对应的测量, 就可以实现对多种不同频率的微波信号进行同步测量。
-
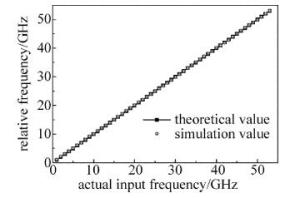
测量误差也是体现该方案是否合理的一个判断标准,将实际输入的频率值与该仿真方案所得到的频率值进行比较分析,可以得到相应的测量误差,测量误差越小证明该测频方案越合理。图 6所示的是微波信号实际输入的频率与仿真频率的比较结果。当实际输入的频率范围为0.5GHz~53GHz时,其实际值与仿真值大致相同,虽然存在一些误差,但是测量效果仍然良好。
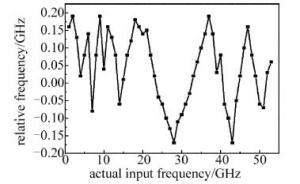
图 7所示的是微波信号实际输入的频率与仿真频率的误差结果。当实际输入的频率范围为0.5GHz~53GHz时,能够看到测量精度不超过±200MHz。其中,所产生的测量误差是由于系统器件级联产生的损耗和器件产生的噪声造成的。
-
本文中提出一种基于相位调制与强度调制相结合的瞬时频率测量的仿真方法。通过幅度比较函数能够快速精准地测量出未知微波信号的频率,并根据理论与仿真的结合来分析其测量特性,从而提高测量范围以及精准度。该方案的频率测量范围可以达到0.5GHz~53GHz,测量误差小于±200MHz,并且结构简易、可靠性强,适用于微波信号的检测和分析,在未来的通信、雷达及电子战等领域中都有着良好的前景。
基于相位和强度调制的微波测频技术研究
Research of microwave frequency measurement based on phase modulation and intensity modulation
-
摘要: 为了更好地对微波信号进行频率测量,采用了一种基于相位调制和强度调制相结合的瞬时测频方法。一束连续波光源通过耦合器被分成两路,未知微波信号分别同时经过相位调制器和强度调制器从而对载波进行调制,之后进入两段长距离的单模光纤中。在光纤中由于色散引起的微波功率损耗的特点,可以获得单调变化的频率-幅度的映射关系,继而通过光电探测的微波信号输出功率比得到幅度比较函数;另外还分析与实现了测频范围与测频精确度的优化。结果表明,该方案结构简易,能够快速精准地测量出未知信号的频率,测量范围可以达到0.5GHz~53GHz,测量误差小于±200MHz。该方法可以有效地测量微波信号频率,可靠性强,适用范围广。Abstract: In order to measure the frequency of microwave signal better, an instantaneous frequency measurement method based on phase modulation and intensity modulation was adopted. A continuous wave light source was divided into two channels by a coupler. Unknown microwave signals passed through both phase modulator and intensity modulator respectively. Accordingly, the carrier was modulated. Then it entered into two long-distance single-mode fibers. Because of the characteristics of microwave power loss caused by dispersion in optical fibers, the mapping relation between frequency and amplitude of monotone change was obtained. Then the amplitude comparison function was obtained by output power ratio of microwave signal detected by photoelectric method. In addition, the range and accuracy of frequency measurement were optimized. The results show that, the structure of the scheme is simple. It can measure the frequency of unknown signal quickly and accurately. The measurement range can reach 0.5GHz~53GHz. The measurement error is less than ±200MHz. This method can effectively measure the frequency of microwave signal and has strong reliability and wide application range.
-
-
[1] ZHANG Y D. Research on high speed and high precision frequency measurement technology[J]. Electronics Quality, 2016 (12):1-3(in Chinese). [2] ZHANG H L. Study on photo-assisted microwave frequency measurement method with improved real-time performance[J]. Chinese Journal of Lasers, 2015, 42(12): 1208008(in Chinese). [3] CHEN L F, MENG R, FENG X. Review of frequency measurement research[J]. Electronic Science and Technology, 2011, 24(2): 155-159(in Chinese). [4] CHEN J. Frequency measurement technique based on microwave photonics[D]. Xi'an: Xidian University, 2017: 1-54(in Chinese). [5] JIANG W. Algorithm of frequency estimation based on correlation coefficient[J]. Journal of Microwaves, 2012, 28(2): 49-52(in Chin-ese). [6] XU D R, HUANG M, WANG C, et al. Design of equal precision digital cymometer[J]. Electronic Science & Technology, 2016, 3(6): 685-688(in Chinese). [7] WANG H, ZHOU W, XUAN Z Q. High-accuracy frequency mea-surement scheme and its implementation[J]. Systems Engineering and Electronics, 2008, 30(5): 981-983(in Chinese). [8] ZOU X H, LUO B, PAN W, et al. Photonics for microwave measurements[J]. Laser & Photonics Reviews, 2016, 10(5): 711-734. [9] MA N. Microwave signal parameter measurement based on microwave photon technology[D]. Xi'an: Xidian University, 2015: 1-79(in Chinese). [10] YANG Sh Sh. Radar signal parameter measurement based on microwave photon technology[D]. Xi'an: Xidian University, 2013: 1-66(in Chinese). [11] NGUYEN L V T. Microwave photonic technique for frequency mea-surement of simultaneous signals[J]. IEEE Photonics Technology Letters, 2009, 21(10): 642-644. doi: 10.1109/LPT.2009.2015890 [12] HUNTER D B, EDVELL L G, ENGLUND M A. Wide band microwave photonic channelised receiver[C]//IEEE International Topical Meeting on Microwave Photonics. New York, USA: IEEE, 2006: 249-252. [13] WANG W S, DAVIS R L, JUNG T J, et al. Characterization of a coherent optical RF channelizer based on a diffraction grating[J]. IEEE Transactions on Microwave Theory and Techniques, 2001, 49(10): 1996-2001. doi: 10.1109/22.954820 [14] AUSTIN M W. Integrated optical microwave channeliser[C]//Communications and Photonics Conference and Exhibition. New York, USA: IEEE, 2009: 1-7. [15] WINNALL S T, LINDSAY A C, AUSTIN M W, et al. A microwave channelizer and spectroscope based on an integrated optical Bragg-grating Fabry-Perot and integrated hybrid fresnel lens system[J]. IEEE Transactions on Microwave Theory and Techniques, 2006, 54 (2): 868-872. doi: 10.1109/TMTT.2005.863052 [16] XING J N, HE H X, CHI H. Research progress of frequency mea-surement of microwave signal based on photonics[J]. Laser Techno-logy, 2018, 42(3): 404-409(in Chinese). [17] YANG Sh Sh. Microwave photon frequency measurement technology based on Optisystem[J]. Electronic Science and Technology, 2013, 26(1): 4(in Chinese). [18] WANG X, HU Z H, FENG Zh H, et al. Application of microwave photon technology in instantaneous frequency measurement[J]. Optoelectronic Technology, 2010, 30(4): 275-278(in Chinese). [19] ZOU X H, YAO J P. An optical approach to microwave frequency measurement with adjustable measurement range and resolution[J]. IEEE Photonics Technology Letters, 2008, 20(23): 1989-1991. doi: 10.1109/LPT.2008.2005505 [20] LI M. Microwave photon instantaneous frequency measurement technology based on comparison function[D]. Xinxiang: Henan Normal University, 2013: 1-60(in Chinese). [21] HU Z H. Realization of instantaneous frequency measurement of radar signals by microwave photon technology[D]. Xinxiang: Henan Normal University, 2011: 1-60(in Chinese). [22] DRUMMOND M V, MONTEIRO P, NOGUEIRA R N. Photonic RF instantaneous frequency measurement system by means of a polarization-domain interferometer[J]. Optics Express, 2009, 17(7): 5433-5438. doi: 10.1364/OE.17.005433 [23] ZHOU J Q, LI J, SHUM P P, et al. Photonic measurement of microwave frequency based on phase modulation[J]. Optics Express, 2009, 17(9): 7217-7221. doi: 10.1364/OE.17.007217 [24] CHI H, ZOU X H, YAO J P. An approach to the measurement of microwave frequency based on optical power monitoting[J]. IEEE Photonics Technology Letters, 2008, 20(14): 1249-1251. doi: 10.1109/LPT.2008.926025 [25] ZHOU J, FU S, ADITYA S, et al. Instantaneous microwave frequency measurement using photonic technique[J]. IEEE Photonics Technology Letters, 2009, 21(15): 1069-1071. doi: 10.1109/LPT.2009.2022637 [26] SHEN T, LAU A, LIU G. OSNR monitoring for higher order modulation formats using asynchronous amplitude histogram[J]. IEEE Photonics Technology Letters, 2010, 22(22): 1632-1634. -


 网站地图
网站地图

 下载:
下载: