Map
HTML
-
为了获得远距离目标更多的细节信息，研究人员不断研制出更大口径的光学望远镜。然而，大口径望远镜面临大气湍流、工程光学技术和制造成本等方面带来的巨大挑战。1704年, 牛顿所著的《光学》一书中描述了大气湍流导致成像模糊和抖动的现象[1]。自适应光学通过对大气湍流引起波前相差的实时探测-控制-校正，使望远系统能够克服大气湍流的动态干扰，获得接近衍射极限的目标像[2]。然而，光波的衍射特性导致望远镜无法分辨遥远目标衍射极限以下的细节信息[3]。
从信息光学上讲，望远镜对远距离目标物的光学成像过程为望远系统点扩散函数与目标物的卷积[4]。望远系统的点扩散函数可理解为望远镜对不同方向平行光线的会聚能力。倘若自适应光学能够理想地校正大气湍流的动态干扰，压缩固定口径望远镜的点扩散函数成为实现超衍射极限角分辨的关键途径。然而，望远镜的通光口径导致整个系统的空间频谱传递是带通截止的，该特性导致衍射压缩成像系统的点扩散函数成为“无法”逾越的障碍。
1952年，TORALDO在理论上将超方向性天线的思想引入高分辨光学成像系统[5]，后续发展成为光瞳滤波技术[6-9]。值得注意的是，英国的BERRY等人明确用数学方法证明了超振荡现象，即一系列低频带限函数在局部区域合成的振荡比低频带限函数的最高频率振荡得更快[10]。超振荡现象意味着局部区域的光斑大小可以摆脱截止频率的限制, 该现象颠覆已有的传统信息光学的认识，理论上能够实现远场区域任意小的光能量会聚[11]。2007年, HUANG等人提出纳米孔结构的可见光超振荡透镜，实验实现了波长660 nm平面波在焦距11.4 μm位置的超衍射聚焦，焦斑大小200 nm(约为0.60倍衍射极限)[12]。2009年，该团队提出预先在焦面位置上理论构造出特定的超振荡光场分布，通过角谱理论反演得到实现构造超振荡光场的空间振幅和位相调制的设计要求[13]。2012年，英国的ROGERS等人实验报道了超振荡透镜结合共焦扫描成像实现最小空间尺寸约1/6的超衍射成像[14]。2015年, LUO团队实验报道了工作波长532 nm下实现0.55倍衍射极限的超振荡望远结果[15]。随后，该团队又提出利用超表面相位调制的近似无色散特征，报道了超表面调制的白光400 nm~700 nm超振荡望远系统，获得了约0.64倍衍射极限的角分辨能力[16]。此外，为解决宽波段超衍射聚焦的轴向色差问题，LUO团队又提出亚波长结构宽带相位调制的设计，报道可见光波段(405 nm~780 nm)的轴向消色差超衍射聚焦结果[17]。TANG团队提出利用结构色散和材料色散补偿消除色差的方法，实现宽带消色差平面光学器件设计[18]。然而，望远镜获取远距离目标信息时常存在大气湍流的动态干扰，目前尚未见基于超振荡原理的望远系统的研究报道。
本文中开展大气湍流动态干扰下超振荡望远成像的理论研究，考虑超振荡光场调制和自适应光学系统校正后波前残差协同作用下，局部衍射压缩望远系统点扩散函数和提高成像分辨率的理论研究。对于632.8 nm的工作波长，中等湍流强度校正后，波前残差均方根约为波长的1/15时引入超振荡望远系统的瞳面，理论研究表明，超振荡望远系统的点扩散函数被局部衍射压缩约0.75倍；超振荡望远系统对不同中心间距双孔的成像结果表明，超振荡望远系统能够获得0.80倍瑞利衍射极限的超分辨成像效果。本研究结合超分辨图像复原算法，为提升轻小型望远系统的角分辨率提供新的技术思路。
-
图 1a所示为大气湍流(atmospheric turbulence, AT)校正后波前残差干扰下，超振荡原理压缩望远系统点扩散函数的原理示意图。图中，I0、D和δ分别为点扩散函数主瓣强度、局部视场大小和半峰全宽, θ为望远系统的视场角。理想平面波E0(r)经过超振荡光学透镜(super-oscillation lens, SOL)调制后，在望远镜的焦平面上形成超振荡光斑。根据标量菲涅耳衍射积分模型，不考虑大气湍流校正波前残差干扰，望远镜在焦平面形成超振荡光斑的强度函数I(ρ)的数学模型为[17]：
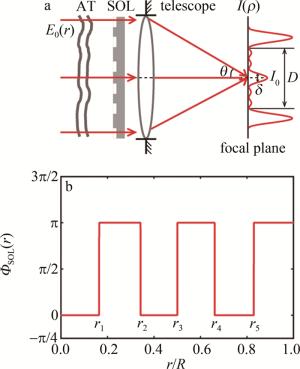
Figure 1. a—residual wavefront interference of atmospheric turbulence correction, schematics of diffraction shrinkage point spread function of telescope with super-oscillation principle b—dependence of the binary phase profile of the super-oscillation lens ΦSOL(r) on telescope radius R
式中，r和ρ分别表示为望远镜瞳面和焦平面的径向坐标，望远镜的工作波长λ和焦距f分别为632.8 nm和1000 mm，望远镜口径为12 mm，ΦSOL(r)为超振荡光学透镜的相位调制函数，J0(·)为零阶贝塞尔函数。根据光的时间反演特性，焦平面光强I(ρ)可通过(1)式逆向线性优化获得相位调制函数ΦSOL(r)。通过初始化约束条件(第一零点位置的压缩比为0.65、暗区视场D=8δ0(艾里斑的第一零点大小δ0=0.61λf/R，R为望远镜半径)、暗区内最高旁瓣/主瓣强度比为0.13)，图 1b所示为线性优化获得能够产生预期焦平面光强I(ρ)的相位调制函数ΦSOL(r)。线性优化获得的π相位突变点r1, r2, r3, r4和r5分别为0.984 mm, 2.055 mm, 3.000 mm, 3.966 mm和4.974 mm。图 1b所示的二元相位调制函数代入(1)式可获得无湍流干扰下超振荡望远系统(super-oscillation telescope, SO-telescope)焦平面和观察线的强度分布，如图 2a和图 2d所示。图 2d表明, 理论设计超振荡望远系统点扩散函数的半峰全宽为0.60δ0，衍射压缩倍率为0.71。
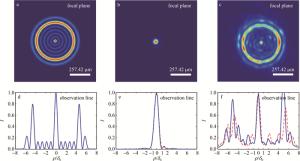
Figure 2. a, d—distribution of focal plane intensity and observation line intensity of SO-telescope of theoretical design b, e—distribution of focal plane intensity and observation line intensity of telescope, after moderate turbulence intensity correction, under interference when RMS of wavefront residual is about 1/15 of wavelength c, f—distribution of focal plane intensity and observation line intensity of SO-telescope, after moderate turbulence intensity correction, under interference when RMS of wavefront residual is about 1/15 of wavelength
图 2所示为无湍流和中等湍流强度下，超振荡衍射压缩望远系统点扩散函数的结果。中等湍流强度下，超振荡望远系统引入工作波长632.8 nm的理想平面波经过自适应光学(adaptive optics, AO)闭环校正后的波前残差均方根(root mean square, RMS)约为波长的1/15时的干扰，AO系统的单元数为137。图 2b和图 2e分别为望远系统焦平面和水平/竖直方向观察线的强度分布。图 2e表明, 仿真艾里斑的半峰全宽约为1.03δ0(δ0=64.355 μm)。对比理想艾里斑尺寸0.84δ0，波前残差导致仿真艾里斑的尺寸存在展宽现象。图 2c所示超振荡望远系统焦平面光强为典型的超振荡光斑，即中心视场的主瓣半高全宽被明显衍射压缩，大气湍流经波前残差干扰后导致暗区的旁瓣强度出现局部干涉相长或相消现象。图 2f表明，理论仿真超振荡光斑的半峰全宽尺寸约为0.773δ0，波前残差导致仿真超振荡光斑与理想超振荡光斑的尺寸0.60δ0存在部分偏差现象；此外，波前残差的随机分布特性导致不同方向观察线的强度分布存在显著差异。图 2表明，中等湍流强度下，超振荡光场调制仍能够实现望远系统点扩散函数的衍射压缩，衍射压缩倍率为0.75(理论设计压缩倍率为0.71)。
-
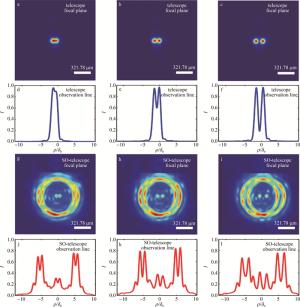
为了验证超振荡望远系统的细节分辨能力，图 3所示为中等湍流强度校正后波前残差均方根约为波长的1/15时的干扰下，中心间距d分别为64.80 μm, 86.40 μm和122.40 μm，直径为46.80 μm双孔的望远成像结果。望远系统的口径和焦距分别为12 mm和1000 mm，在632.8 nm的工作波长下，瑞利判据可分辨的理论极限为64.355 μm。图 3a和图 3d表明，望远系统无法分辨中心间距64.80 μm的双孔，波前残差导致望远系统点扩散函数展宽，从而导致成像对比度为0。图 3g和图 3j表明，超振荡望远系统能够清楚地分辨双孔，成像对比度为0.154。对比结果表明，超振荡望远系统具备超衍射极限成像的能力。图 3b和图 3c表明，望远系统能够分辨中心间距86.40 μm和122.40 μm双孔；由图 3e和图 3f观察线强度分布可知，成像对比度分别为0.228和0.683。望远系统成像对比度随着中心间距的变化规律，符合理论的预期。与此同时，超振荡望远系统对中心间距86.40 μm和122.40 μm双孔的成像对比度分别为0.397和0.578，如图 3k和图 3l所示。对比图 3a和图 3b、图 3h和图 3i的成像结果, 证明了大气湍流下超衍射望远成像的能力。
Figure 3. Distribution of two holes imaging with different center-to-center distances of telescope and SO-telescope, after moderate turbulence intensity correction, under interference when RMS of wavefront residual is about 1/15 of wavelength
1.1. 局部衍射压缩点扩散函数
1.2. 超振荡望远成像仿真
-
图 4中蓝色圆点和红色方块曲线分别为望远系统和超振荡望远系统对不同中心间距双孔的成像对比度变化规律。虚线表示瑞利判据时的对比度0.153。依据瑞利判据，理想望远成像系统的分辨率极限应为δ0，即中心焦距小于δ0的物体无法分辨。中等湍流强度校正后，波前残差均方根约为波长的1/15时的干扰下，望远系统点扩散函数存在展宽，导致成像分辨率极限约1.25δ0，如图 4蓝色圆点曲线所示。由图 4中红色方块曲线可知，超振荡望远系统的成像对比度和分辨率都得到提高，分辨率极限约1.00δ0，为望远系统分辨率极限的0.80倍。值得注意的是，中心间距d>1.75δ0的成像结果表明：超振荡望远系统暗区内的旁瓣强度会导致其成像对比度比望远系统成像对比度更小。
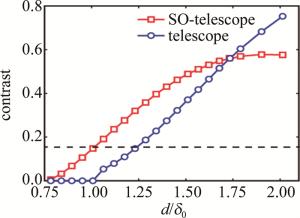
Figure 4. Distribution of imaging contrast of two holes with different center-to-center distances of telescope and SO-telescope, after moderate turbulence intensity correction, under interference when RMS of wavefront residual is about 1/15 of wavelength
对于扩展目标、离散多点目标的成像，超振荡望远系统点扩散函数的高强度旁瓣存在干扰，无法采用单视场成像方式体现目标物的细节信息。对于这种情况，可以通过成像平面引入视场光阑，避免视场外的光线干扰成像结果；再结合视场拼接方式实现扩展目标、离散点目标的大视场、超衍射极限成像。值得注意的是，本文中的研究只考虑中等湍流强度校正后, 波前残差均方根约为波长的1/15时的干扰下，中等湍流强度校正后波前残差的均方根大小可能会导致望远系统点扩散函数的衍射压缩倍率和成像分辨率存在差异；此外，强湍流校正后，波前残差均方根约为波长的1/15时的干扰下，超振荡光场调制无法衍射压缩望远系统的点扩散函数，该现象已经在作者的实验测试中得到验证。初步分析原因：强湍流导致望远镜瞳面的光场振幅闪烁，导致超振荡位相调制方法存在不足。
-
开展了大气湍流下超振荡光场局部衍射压缩望远系统点扩散函数和提高成像分辨率的理论研究。中等湍流强度校正后，波前残差均方根约为波长的1/15时的干扰下，超振荡光场调制能够实现望远系统点扩散函数的衍射压缩，衍射压缩倍率为0.75。对不同中心间距双孔的成像研究验证了超振荡望远系统约0.80倍瑞利衍射极限的超分辨成像效果。波前残差的均方根大小可能会导致望远系统点扩散函数的衍射压缩倍率和成像分辨率存在差异。本文中的研究内容有望应用于高精度星点定位、超分辨成像等领域[19]。
DownLoad: